自适应变体机翼可以通过光滑而连续的改变机翼形状来适应不同的飞行条件。由于后缘偏转可通过有效改变翼型弯度而大幅影响机翼气动性能,柔性变后缘机翼一直是自适应机翼研究的重要内容。其中最著名的是NASA/DARPA/AFRL联合开展的智能机翼计划(Smart Wing Program,见图 1)[1-6]。该项目着重研究机翼扭转及无铰链操纵面技术,采用智能材料SMA(形状记忆合金)扭力管控制机翼操纵面的偏转,以实现机翼多自由度无缝光滑连续变形。该项目先后进行了3期风洞试验,最大试验马赫数0.9,试验结果表明这种无铰链操纵面能有效地减小机翼巡航阻力,同时在滚转力矩控制方面的效果也较为明显。

|
| 图 1 SWP计划风洞试验与模型照片 Fig.1 SWP program wind tunnel test and model photo |
近年,NASA和波音公司正在联合研制一种可连续变弯度后缘襟翼(VCCTEF)(见图 2)[7-9],目的是随飞机重量和巡航条件的变化来改变机翼的扭转角与弯度,从而减小飞机巡航阻力。机翼的外翼由42个小襟翼段构成,组成了14组“3段式襟翼”。前端2个小襟翼段采用SMA驱动,其特点是结构重量轻,但响应速度慢,变形速度约为10°/min。末端襟翼段采用较重、但响应速度快的旋转电机驱动,起到了副翼作用。作为增升装置使用时,它还消除了传统后缘襟翼的开缝,大大降低起降噪声。

|
| 图 2 连续可变弯度后缘襟翼试验照片 Fig.2 The test photo of variable camber continuous trailing edge flap |
此外,加拿大魁北克大学提出了一种可变翼型机翼,变形系统由上翼面柔性蒙皮、形状记忆合金驱动器组和刚性内基构成。通过Ma=0.2、0.3风洞实验表明,在迎角从-1°~2°变化过程中阻力减小量从14.5%变化到26.7%,平均减小18.5%。改变翼型厚度可以改变升力系数和阻力系数,从而满足飞行器对不同飞行状态的需求[10]。
U.Icardi等人设计了一种形状记忆合金扭力管驱动的变体机翼。通过有限元仿真得到了形状记忆合金所要提供的驱动力、力矩以及机翼可承受的气动载荷。计算结果表明,在900km/h的巡航速度下,该机翼后缘偏转可达到平均21.7°,其中翼尖旋转最大可达40°[11-12]。
可以看出,目前变形体机翼的设计研究大多采用智能材料结构,驱动元件以形状记忆材料为主,优点是重量轻,体积小,结构上容易实现[13]。国内也开展了许多智能材料结构在变体机翼设计应用方面的研究[14-16]。哈尔滨工业大学冷劲松等人开展了形状记忆聚合物蒙皮在变弯度机翼上应用的研究[14],在中国航天空气动力技术研究院进行了低速风洞试验,试验来流速度12m/s;南京航空航天大学徐志伟等设计了一种由形状记忆合金驱动的分段式变后缘结构,对形状记忆合金驱动元件的布局进行了理论计算[15-16],并进行了空载与加载状态下结构运动实验研究。纵观国内,目前的试验研究还集中在低速范围内,关于变形体模型在亚跨声速状态下的试验研究还未见报道。适用于亚跨声速风洞试验的模型变形结构以及变形对模型气动性能的影响规律还有待进一步研究与探索。
本文针对一套后缘偏角可光滑连续改变的二元机翼模型,在高速风洞中利用模型变形视频测量技术(Videogrammetric Model Deformation, VMD)对模型变形进行了测量,验证了气动载荷作用下所设计结构的变形能力,同时还研究了后缘偏转对上翼面压力分布的影响规律。
1 试验模型本文提出了一种悬臂梁式柔性偏转结构。其作动原理为:当形状记忆合金升温时,合金收缩驱动柔性节偏转并带动整个机翼后缘偏转,柔性节偏转时将储存一定的弹性势能;当形状记忆合金冷却时,弹性势能释放,形状记忆合金被重新拉伸,可供下一次变形驱动。变形结构原理图如图 3所示。

|
| 图 3 后缘偏转原理图 Fig.3 Trailing edge deflection principle diagram |
选取的基准翼型为NASAsc-0714(2) 超临界翼型。试验模型展长365mm,弦长150mm。0°迎角堵塞度约为2%。形状记忆合金丝缠绕在机翼腹腔两侧的齿状接头上,采用压紧螺钉将形状记忆合金丝两端固定。具体连接形式如图 4(a)所示。考虑到形状记忆合金丝排布疏密对安装难易的影响,经多次试验后决定选取接头齿间间距为15mm,即365mm展长的模型总共可以布置40根丝,如图 4(b)所示。本文采用的形状记忆合金丝为西安赛特金属材料开发有限公司生产的钛镍合金丝(镍原子数分数为50.1%)。形状记忆合金丝的相变温度为:MS=20℃,Mf=9℃,AS=45℃,Af=56℃。丝直径1mm,预应变5.6%。采用漆包线间接加热形状记忆合金丝。由恒流稳压电源供电,加热电流2.5A,稳定后对应温度约为60℃。冷却时,关闭电源停止加热,采用自然冷却的方式。通过控制电源的开断控制变形。

|
| 图 4 模型装配示意图 Fig.4 Schematic diagram of model assembly |
安装形状记忆合金前对其进行预拉伸,并在安装时保留一定预紧力。驱动机构安装完成后,用玻璃胶填充整个机翼腹部空腔,并进行修型(见图 5)。

|
| 图 5 机翼剖面 Fig.5 Photo of the model's wing section |
为验证所提出的柔性节的变形能力,在地面使用三坐标机测量了机翼变形前后的剖面图(见图 6和7)。结果表明,模型后缘最大偏转位移为9.65mm,对应的后缘偏转角为10.9°,单程变形时间约为120s。结构变形前、变形后机翼型面均实现光滑过渡。作为原理验证模型,加热方式较为简单,其变形速度与调研文献中10°/min的变形速度相比略慢,还有待提高。

|
| 图 6 测量现场照片 Fig.6 Photo of measurement setup |

|
| 图 7 三坐标机测量结果 Fig.7 Three coordinate measuring results |
采用VMD技术和连续测压技术分别测量了模型后缘偏转变形量以及上翼面压力分布。试验条件如表 1所示。
| 流场参数 | 数值 | ||||
| Ma | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| AOA/(°) | 0°、2°、4°、6° | ||||
| Re/106 | 1.27 | 1.54 | 1.81 | 2.11 | 2.32 |
| Dynamic pressure/Pa | 9891 | 14619 | 20143 | 26532 | 32258 |
试验在中国空气动力研究与发展中心0.6m×0.6m风洞中进行。该风洞是一座半回流暂冲式亚跨超声速风洞。试验段横截面0.6m×0.6m,上、下壁板可以更换,左右壁板固定。风洞试验马赫数范围为0.4~3.5。本期试验选用特种试验段,该试验段上下壁板为槽壁,左右壁板为实壁,左右壁板各有一个方形光窗,适合VMD拍照和摄像。
模型通过专用接头安装在特种试验段下壁板(见图 8)。规定:x方向为气流方向,y方向垂直于来流向下,z方向由右手坐标法则确定。模型加热变形后,机翼后缘会在x-z平面内,向-z方向偏转。

|
| 图 8 模型在风洞中安装图 Fig.8 Model in the wind tunnel |
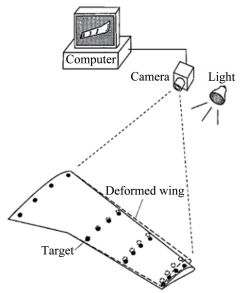
VMD是一种光学测量手段,可通过一系列带有标记点的照片确定模型表面的空间坐标位置,进而确定目标变形量[17]。该技术特别适用于测量风洞试验时机翼及操纵面的变形。如图 9所示,VMD系统的硬件组成包括:工业相机与镜头、工控机、光源以及模型表面的标记点。
|
| 图 9 单相机VMD测量系统架构 Fig.9 Single camera VMD measurement system |
试验模型表面标记点位于上翼面,具体位置如图 10所示,后缘从翼稍到翼根依次标记为0~17号,前缘从翼稍到翼根依次标记为18~35号,共18组。每组标记点间左右间隔20mm,标记点距前后缘距离均为5mm。试验使用的VMD系统,由中国空气动力研究与发展中心自主开发研制,系统动态角度测量精度可达0.01°。

|
| 图 10 上翼面VMD标记点位置示意图 Fig.10 Position of the upper wing's VMD mark point |
VMD系统通过对每一帧图片进行解算,可获得标记点在虚拟坐标系中的坐标值。具体的后缘偏转位移与偏转角需要根据标记点的坐标值计算而得。计算方法如下:
待风洞流场稳定后,VMD系统开始测量,同时变形开始。第1帧图像记录的是测量剖面的变形前翼型。在变形过程中,由于后缘偏转导致气动力变化会使模型发生沿展向的上反变形,因此变形后的翼型剖面如图 11所示,与未变形的翼型剖面在空间上是不重合的。定义Zin为变形过程中第n帧数据记录的标记点i在Z方向坐标。后缘偏角θp的计算公式为:
 (1)
(1)
 (2)
(2)

|
| 图 11 后缘偏转角计算示意图 Fig.11 Calculation sketch of trailing edge deflection angle |
式中:r为后缘端点到柔性节起点的直线距离。
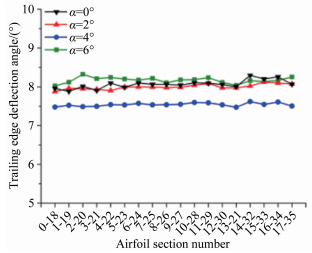
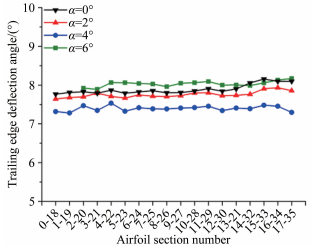
图 12~16所示为处理后的后缘偏转角分布图。图中横坐标为所测量的18个机翼剖面的编号,纵坐标为机翼的后缘偏转角。其中Ma=0.6、0.7和0.8,迎角为6°时,风洞起动瞬间,翼稍处受冲击瞬间姿态变形较大,标记点丢失,未获得变形数据。

|
| 图 12 Ma=0.4后缘偏转角分布测量结果 Fig.12 Measurement results of trailing edge deflection angle when Ma=0.4 |
|
| 图 13 Ma=0.5后缘偏转角分布测量结果 Fig.13 Measurement results of trailing edge deflection angle when Ma=0.5 |
|
| 图 14 Ma=0.6后缘偏转角分布测量结果 Fig.14 Measurement results of trailing edge deflection angle when Ma=0.6 |
|
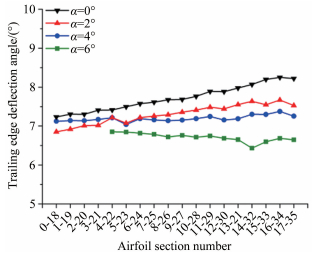
| 图 15 Ma=0.7后缘偏转角分布测量结果 Fig.15 Measurement results of trailing edge deflection angle when Ma=0.7 |
|
| 图 16 Ma=0.8后缘偏转角分布测量结果 Fig.16 Measurement results of trailing edge deflection angle when Ma=0.8 |
(1) 马赫数越大偏角分布越不均匀
通过图 12~16可以看出:Ma=0.4和0.5时,模型后缘的变形均较为均匀,最大偏差在0.2°以内。Ma=0.6~0.8偏转角分布沿翼稍至翼根逐渐增大,其中Ma=0.7最大最小偏角相差0.82°。这是由于模型采用悬臂支撑,在气动力作用下存在扭转姿态变形,致使不同测量剖面的实际迎角有所不同,进而导致不同剖面的气动载荷大小不同,因此在高马赫数、高气动载荷时,偏转角分布并不均匀。其中,Ma=0.7接近翼型的临界马赫数,迎角的微小变化会对模型上翼面流态产生较大的影响,因此分布变化最为剧烈。
(2) 马赫数越大变形能力越差
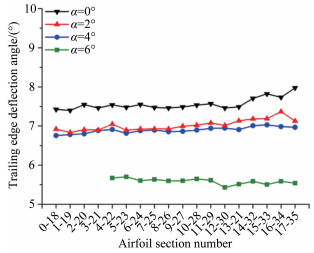
图 17给出了迎角为2°时,不同马赫数状态下的后缘偏转角分布。从图中可以看出,随着马赫数的增加,后缘偏转角逐渐降低,模型的变形能力逐渐减弱。Ma=0.4时,后缘偏转角可达8.05°,Ma=0.8时,后缘偏转角为6.9°(以中间8-26剖面为例)。

|
| 图 17 α=2°后缘偏转角分布测量结果 Fig.17 The measurement results of the angle distribution when α=2° |
对变化过程曲线求导,可以获得后缘偏转角速度的动态变化历程, 由图 18给出。从图中可以看出,最大变形角速度随马赫数的增加逐渐降低。
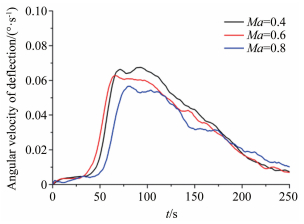
|
| 图 18 α=2°后缘偏转角速度测量结果 Fig.18 The measurement results of the angular velocity of deflection when α=2° |
由图 12~16可知,小马赫数时迎角对后缘偏角的影响较小。Ma=0.4、0.5和0.6时,迎角为0°、2°和6°这3条曲线聚集在一起。而Ma=0.7和0.8的后缘偏角分布曲线间相距明显加大。Ma=0.4时,不同迎角状态所对应的后缘偏转角最大相差0.57°;Ma=0.8时,相差1.86°。因此随着马赫数的增加,迎角对模型变形能力的影响逐渐增强。
选取某一固定剖面的后缘偏转变形为例进行分析。考虑到翼稍处存在一定的三维流动效应,而翼根处模型的扭转变形分布不均匀,本文选取翼段中部的8-26剖面进行分析,图 19为后缘偏角对比图。

|
| 图 19 最大后缘偏转角测量结果 Fig.19 Measurement results of maximum trailing edge deflection angle |
由图可知,当Ma=0.4~0.6时,后缘偏转角在4°迎角时达到最小值;Ma=0.7、0.8时,后缘偏转角随迎角增大单调递减。
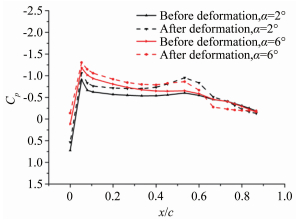
图 20和21给出了Ma为0.5与0.7时变形前后上翼面压力分布。Ma=0.5,迎角为6°与其他几个迎角状态相比(这里以2°迎角为例),由于迎角增大,变形后机翼后缘流动不能再附着,发生了流动分离。分离后机翼后缘的压力分布角明显增大,导致6°迎角时上翼面后缘吸力及其对柔性节的力矩显著降低。解释了低马赫数时,后缘偏角随迎角增大而先减小后增大现象产生的原因。Ma=0.7时,各个迎角状态下变形均会导致后缘发生流动分离(这里以2°、6°迎角为例)。且分离流后,后缘的压力系数大小相近,即上翼面吸力产生的力矩相差不大。后缘偏角随迎角增大而递减可能是由于变形后下翼面流动受阻碍,压力系数升高,下翼面升力增加造成的。
|
| 图 20 Ma=0.5变形前后压力分布对比 Fig.20 Comparison of pressure distribution before and after deformation when Ma=0.5 |

|
| 图 21 Ma=0.7变形前后压力分布对比 Fig.21 Comparison of pressure distribution before and after deformation when Ma=0.7 |
另一方面,通过对比变形前后的压力分布曲线可以看出,后缘偏转能明显改变上翼面的压力分布。在低马赫数状态,能加快上翼面的绕流流速,起到增升的作用。在临界马赫数附近,变形会使机翼前缘压力平台扩张,柔性偏转处产生一负压峰,升力系数增加。但同时会致使后缘发生流动分离,增大压差阻力。
4 结论通过对柔性变后缘机翼模型动态测变形、测压试验结果的分析,可以得出以下结论:
(1) 模型采用的智能材料结构在高速气动载荷作用下能实现后缘偏角连续光滑变形,且后缘偏转变形能明显改变上翼面压力分布形态。该结构可应用于柔性变后缘机翼气动特性风洞试验研究中。
(2) 气动力作用下,机翼后缘偏转角最大可达8.4°,最小5.6°。偏转角分布在低马赫数时较为均匀,在高马赫数时由翼稍至翼根逐渐增加。
(3) 来流条件对所提出的智能材料结构的变形能力影响显著。随马赫数的增加,最大后缘偏角逐渐降低,变形速率也逐渐减小。迎角的影响与马赫数相耦合。马赫数越高迎角的影响越强。在低马赫数时,随迎角增大,后缘偏转角先增后减;高马赫数时,随迎角增大,偏转角单调递减。通过对后缘压力分布形态的分析得出,变形后后缘是否发生流动分离是影响智能材料结构变形能力的关键因素。
| [1] | Wlezien R W, Horner G C, McGowan A M R, et al. Aircraft morphing program[C]//5th Annual International Symposium on Smart Structures and Materials, International Society for Optics and Photonics, 1998:176-187. |
| [2] | Kudva J N. Overview of the DARPA smart wing project[J]. Journal of Intelligent Material Systems and Structures, 2004, 15(4): 261–267. DOI:10.1177/1045389X04042796 |
| [3] | Kudva J N, Jardine A P, Martin C A, et al. Overview of the ARPA/WL smart structures and materials development-smart wing contract[C]//1996 Symposium on Smart Structures and Materials, International Society for Optics and Photonics, 1996:10-16. |
| [4] | Martin C A, Jasmin L, Flanagan J, et al. Smart wing wind tunnel model design[C]//Proc SPIE, 1997, 3044:41-47. |
| [5] | Scherer L B, Martin C A, Appa K, et al. Smart wing wind tunnel test results[C]//Smart Structures and Materials'97, International Society for Optics and Photonics, 1997:56-66. |
| [6] | Scherer L B, Martin C A, West M N, et al. DARPA/ARFL/NASA Smart Wing second wind tunnel test results[C]//1999 Symposium on Smart Structures and Materials, International Society for Optics and Photonics, 1999:249-259. |
| [7] | Precup N, Mor M, Livne E. Design, construction, and tests of an aeroelastic wind tunnel model of a variable camber continuous trailing edge flap (VCCTEF) concept wing[R]. AIAA-2014-2442, 2014. |
| [8] | Precup N, Mor M, Livne E. The design, construction, and tests of a concept aeroelastic wind tunnel model of a high-lift variable camber continuous trailing edge flap (HL-VCCTEF) wing configuration[C]//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. 2015. doi:10.2514/6.2015-1406. |
| [9] | Ting E, Dao T, Nguyen N. Aerodynamic load analysis of a variable camber continuous trailing edge flap system on a flexible wing aircraft[C]//56th AIAA/ASCE/AHS/ASC Struc-tures, Structural Dynamics, and Materials Conference, 2015. doi:10.2514/6.2015-1839. |
| [10] | 陶宝祺. 智能材料结构[M]. 北京: 国防工业出版社, 1997. Tao B Q. Intelligent material structure[M]. Beijing: National Defence Industry Press, 1997. |
| [11] | Icardi U, Ferrero L. Preliminary study of an adaptive wing with shape memory alloy torsion actuators[J]. Materials & Design, 2009, 30(10): 4200–4210. |
| [12] | Brailovski V, Terriault P, Georges T, et al. SMA actuators for morphing wings[J]. Physics Procedia, 2010, 10(12): 197–203. |
| [13] | Coutu D, Brailovski V, Terriault P. Optimized design of an active extrados structure for an experimental morphing laminar wing[J]. Aerospace Science & Technology, 2010, 14(7): 451–458. |
| [14] | 陈钱, 白鹏, 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析[J]. 空气动力学学报, 2010, 28(1): 46–53. Chen Q, Bai P, Ying W L, et al. Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J]. Acta Aerodynamica Sinica, 2010, 28(1): 46–53. |
| [15] | 杨媛, 徐志伟. 基于SMA的飞行器变体机翼驱动结构研究[J]. 兵器材料科学与工程, 2010, 33(1): 25–30. Yang Y, Xu Z W. Research of the wing structure based on a shape-memory alloy actuated morphing wing[J]. Ordnance Material Science and Engineering, 2010, 33(1): 25–30. |
| [16] | 刘俊兵, 王帮峰, 芦吉云, 等. 基于SMA的差动式变体机翼后缘驱动器研究[J]. 兵器材料科学与工程, 2015, 38(4): 14–18. Liu J B, Wang B F, Lu J Y, et al. Differential SMA actuator in trailing edge of morphing wing[J]. Ordnance Material Science and Engineering, 2015, 38(4): 14–18. |
| [17] | Burner A W, Liu T. Videogrammetric model deformation measurement technique[J]. Journal of Aircraft, 2001, 38(4): 745–754. DOI:10.2514/2.2826 |



