在我国大型客机气动设计中,民机的气动减阻一直是目前面临的主要挑战之一,具有很重要的意义。在飞机翼尖处产生的诱导阻力是飞机飞行时受到阻力的重要组成部分,在巡航状态时约占飞机总阻力的40%,有很大的减阻空间[1]。根据诱导阻力的定义可知,飞机翼尖处的诱导阻力是由于飞机翼尖处的翼尖涡诱导引起的[2-3]。阻碍或者破坏翼尖涡结构形成,设法消除翼尖处的集中涡,使洗流具有均匀的分布是目前飞机诱导阻力减阻的主要措施[4-7]。因此,本文将结合翼尖涡的物理特征和机翼翼尖的诱导阻力研究翼尖诱导阻力的减阻方法,并揭示相应的减阻机制,进而指导飞机机翼的翼尖设计。
实验和数值计算[8-10]是现阶段研究翼尖涡引起的诱导阻力减阻的2种主要方法。C. S. Lee等人[11-12]通过在翼尖处增加喷流装置进行实验,发现翼尖涡的涡核会随着喷流方向的不同而改变,从而导致翼尖处诱导阻力的变化。Margaris和Gursul[13]等人研究了喷流装置的喷口位置对翼尖涡的影响,发现不同的喷口位置对翼尖涡结构的改变是不同的。F. M. Catalano等人利用热线风速仪进行实验研究,发现降低翼尖涡强度会削弱翼尖涡引起的下洗流动,从而降低翼尖涡引起的诱导阻力[14]。Luis Falcao和德国Saarland大学的Christian Boiler等人通过数值研究发现,增强翼尖涡的耗散能力,会提高相应的翼尖诱导阻力的减阻效果[15-16]。由此,根据前人的研究可知,翼尖涡的物理特征与诱导阻力之间存在紧密的联系[17-22]。本文将通过风洞实验进一步研究它们之间的关系,揭示诱导阻力减阻机制。
实验中,为了测量翼尖处的诱导阻力,本文提出并设计了一套翼尖气动阻力的测量装置。装置中传感器测量的阻力方向始终与风洞轴线平行,不会随机翼迎角的变化而变化,即始终平行于来流方向,这种测量阻力的方法可以不通过坐标变换直接测量阻力,从而避免引入由角度测量偏差引起的阻力误差。同时,与翼尖涡的物理特征相结合,进而分析基于翼尖涡物理特征的翼尖减阻原则,为以后机翼翼尖的设计提供基础数据和理论指导。
综上所述,本文的工作具体分为以下几个部分。第一部分是研究概述,第二部分是实验装置的介绍,第三部分是翼尖涡物理特征与诱导阻力的测量与计算,第四部分是基于翼尖涡物理特征的诱导阻力减阻机制研究,最后一部分是对本文工作的总结。
1 实验装置本实验是在上海交通大学的低速回流式风洞中进行的。风洞收缩比为6.25,试验段截面形状为矩形,截面尺寸为1.2m×0.9m,长2m。实验中的最低风速为10m/s,最高风速为70m/s。在试验段上游,通过收缩段前面的蜂窝网状结构整流,以降低实验段中的湍流度。为了提高流场品质,实验前需要对风洞流场进行校验。通过热线风速仪测量得到风洞自由来流的湍流度为0.05%,图 1为风洞实验装置简图。
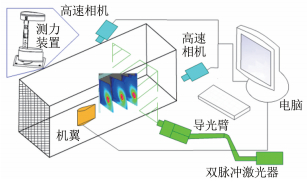
|
| 图 1 风洞实验装置示意图 Fig.1 Experimental setup in wind tunnel |
实验中采用简化的机翼模型,机翼翼型选为NACA0020。机翼采用铝合金材料加工,弦长为25cm,如图 2所示。通过改变机翼的展长高度来满足实验所需的展弦比。展向长度范围为25~65cm,即展弦比为1~2.69。机翼模型安装在有刻度的水平转盘上,水平转盘固定在风洞底面上,转动水平转盘即可变换机翼模型的迎角。为了减小前缘涡的分离,实验中采用的迎角范围为0°~12°[23]。其中,0°迎角机翼模型的翼尖位于风洞中心轴线上, 如图 2所示。进行翼尖涡的流场测试时, 风速V∞=20m/s,以模型弦长为参考长度的雷诺数Re=3×105。

|
| 图 2 机翼模型的风洞安装示意图 Fig.2 Installation of wing model in the wind tunnel |
实验中采用三维PIV系统进行图像采集。其中,三维PIV系统是利用2台型号为Imager-Pco的高分辨率CCD相机进行拍摄,相机的最高分辨率可达4032pixel×2688pixel,图像采集速率为1帧/s。相机镜头采用NIKKOR 100mm 1:1.4D定焦镜头,并通过532nm波长的带通滤光镜来提高图像信噪比。2台相机并不正对着激光面,而是与之成一定的夹角。实验中,相机与镜头与激光面之间的倾斜角必须满足Scheimpflug条件[24]。在本实验中,激光片与CCD相机记录的平面相距1000mm,2个相机之间的夹角为60°。此时,三维PIV的拍摄窗口大约200mm×200mm。激光器则选用双脉冲Nd: YAG激光器,激光面与试验段高透明度玻璃垂直,激光光片厚度为0.5~3mm可调。CCD相机与双脉冲Nd: YAG激光共同连接到同步器的延迟系统上,以此来实现激光发射与图像采集之间的同步。通过Insight软件对3DPIV拍摄的流场进行处理,得到流场中的翼尖涡结构信息。
风洞中,示踪粒子选为乙二醇加热后产生的烟雾,发烟器置于机翼模型下游的风洞管道内,粒径为1μm≤d≤5μm。为了保证粒子布撒的均匀性,粒子将在风洞中循环几次,从而可以减轻粒子不均匀对流场的影响。测量时,片光垂直来流方向且距离翼尖后缘100mm,2个相机与片光成30°夹角,记录片光内示踪粒子的运动轨迹。每个实验状态均采集300帧图像,进行时均处理后,可得到该状态下的流场信息。
1.2 诱导阻力测量系统Gharib等人[19]在研究平板翼起动过程中翼尖涡对阻力的影响时,根据平板翼表面的流动结构将平板翼分成2个区域,即准二维区域和翼尖涡影响的三维区域。本文基于该思想,设计了一套机翼翼尖气动力测量装置,通过该装置测量机翼翼尖处的翼尖涡引起的气动阻力。装置模型如图 3所示,该气动力测量装置将机翼分为2部分,主机翼部分与翼尖部分。传感器不与主机翼部分相连,而是与翼尖部分直接连接,由此可测量翼尖处的气动阻力。
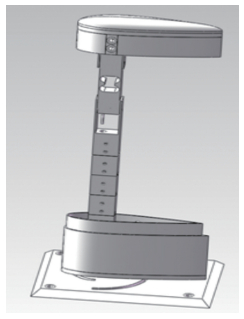
|
| 图 3 测力装置模型图 Fig.3 Model of force measuring system |
实验中,主机翼和传感器分别安装在底板上,两者不相连。在改变主机翼迎角时,同时改变传感器与翼尖的相对位置,使机翼翼尖与主机翼迎角相同。由于传感器固定在底板上并不与主机翼相连接,传感器始终保持不动,即其测量方向始终不变,可以保证测量得到的气动力为机翼受到的气动阻力,此时,该气动阻力为机翼受到的总阻力。在来流速度较低的情况下,机翼的总阻力可以分为翼型阻力和诱导阻力。其中,翼型阻力可以通过测量不同展弦比下准二维区域的阻力计算得到。进行一个假设:翼型阻力在三维翼尖涡影响区域不发生变化。因此,通过传感器测量的总阻力减去上面计算求得的准二维翼型阻力即可以获得翼尖处翼尖涡引起的诱导阻力。
为了能够精确测量翼尖处的气动力,在实验中选用HBM的高精度的SP4M单分量传感器测量与来流平行的气动力,即气动力中的阻力。传感器量程为5kg,测量精度可达万分之二,所以可以很好地满足实验的需要。单分量传感器测量得到的翼尖处的气动力信号通过NI公司型号为NI PXIe-1071的数据采集系统来采集,采样频率为200Hz。数据采集系统与电脑相连,将数据读入电脑中。之后将采集得到的数据通过MATLAB程序进行再一次的滤波处理。
2 机翼翼尖涡的物理特征与诱导阻力在实验中,风洞的风速范围设定在10~70m/s,机翼的弦长C=25cm,展弦比为2,即机翼展长为50cm,机翼的迎角为4°、6°、8°、10°和12°。为了分析近壁面翼尖涡结构的生长演化过程,将用3DPIV来进行实验,记录尾迹中距离机翼尾缘不同弦长处的近壁面翼尖涡结构。
机翼翼尖涡的无量纲环量:
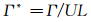 (1)
(1)
式中:Γ为翼尖涡结构的环量;U为风洞的风速;L为翼尖涡的特征尺寸。
2.1 机翼翼尖涡的物理特征图 4给出了迎角为6°时距离机翼尾缘不同截面处的翼尖涡结构。图中的截面从右至左分别为距离机翼尾缘1倍弦长、2倍弦长、3倍弦长和4倍弦长截面处的翼尖涡结构。图 4左上角中的rc为翼尖涡涡核与机翼尾缘翼尖处之间的无量纲距离。
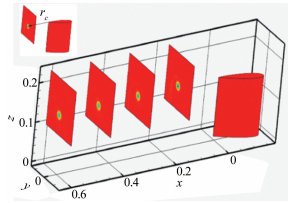
|
| 图 4 6°迎角下机翼尖涡云图 Fig.4 Contour of the tip vortex of wing with the angle of attack at 6° |
从图 4可以看到,机翼翼尖涡向下游传输的过程中也会不断地向翼根处移动,同时翼尖涡的强度在脱落之后基本保持不变,即翼尖涡已经处于稳定阶段。
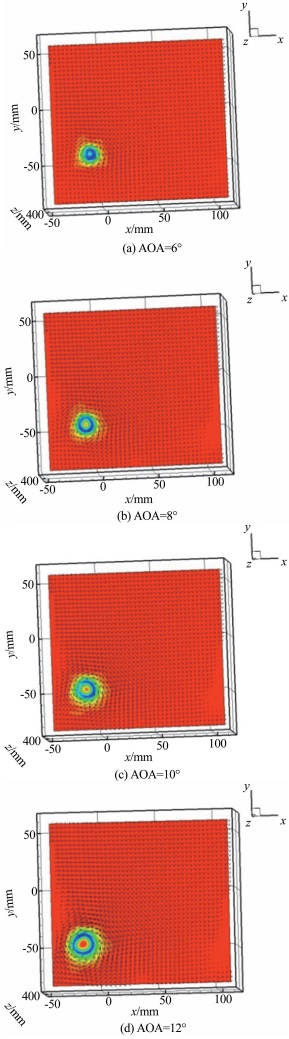
图 5给出了风速U=15m/s时,在D/C=4截面处,不同迎角下的翼尖涡结构的速度场和涡量云图。
|
| 图 5 不同机翼迎角下的翼尖涡的瞬时速度场和涡量云图 Fig.5 Instantaneous velocity (arrows) and vorticity (color) fields of the tip vortex of wing with different angles of attack |
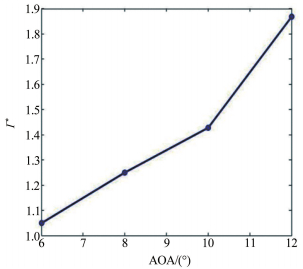
从图 5中可以看到,翼尖涡会随着机翼迎角的增大而增大。图 6给出了翼尖涡对应的无量纲环量变化曲线图。从图 6中可以看出,翼尖涡的无量纲环量随着机翼迎角的增大而不断地增大。在迎角较小时(在6°~10°变化),翼尖涡的无量纲环量随迎角的增加较缓。在迎角较大时(从10°到12°),翼尖涡的无量纲环量随迎角的增加变得较大。
|
| 图 6 不同迎角对翼尖涡的无量纲环量的影响 Fig.6 Non-dimensional circulation of vortex structure on wingtip influenced by the angle of attack |
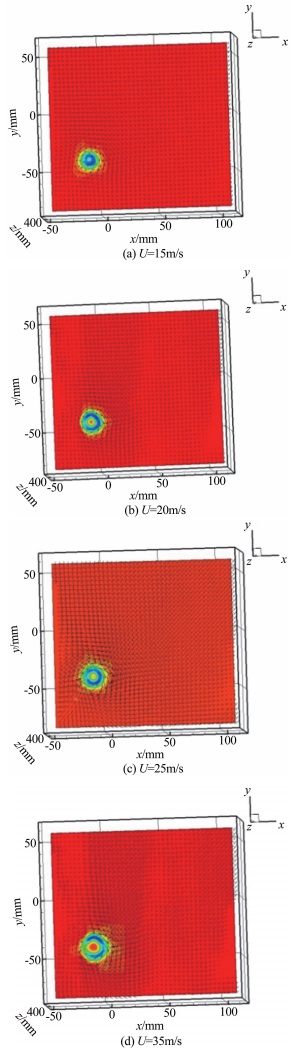
图 7给出了迎角为6°时,在D/C=4截面处,不同风速下翼尖涡结构的速度场和涡量云图。
|
| 图 7 不同风速下的翼尖涡的瞬时速度场和涡量云图 Fig.7 Instantaneous velocity (arrows) and vorticity (color) fields of the tip vortex of the plate wing with different velocities |
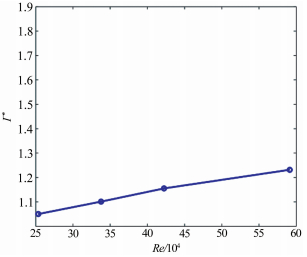
从图 7中可以看到,翼尖涡随着迎角的增大不断地增大。图 8给出了翼尖涡的无量纲环量随雷诺数的变化规律。从图中可以看到,随着雷诺数的增大,翼尖涡的无量纲环量也会随之增大。这主要是由于随着雷诺数的增大,翼尖处脱落的涡结构更强。
|
| 图 8 不同雷诺数对翼尖涡的无量纲环量的影响 Fig.8 Non-dimensional circulation of vortex structure on wingtip influenced by the Reynolds number |
为了得到翼尖部分的翼尖阻力,将机翼根据其表面流动分为准二维区域和翼尖三维区域[19, 25]。准二维区域气动力的改变呈线性变化,翼尖三维区域的气动力呈非线性变化。实验中将改变翼尖部分的高度,测量不同高度翼尖的气动阻力,由此确定翼尖处受到的气动阻力。不过,此时测量得到的翼尖处的气动阻力包括诱导阻力和型阻2部分。此外,根据文献[25], 型阻会随着测量高度的增大逐渐增大,诱导阻力则不会随高度增加而增大。那么,可根据测量得到的不同高度翼尖处的气动阻力估算出相应的诱导阻力。
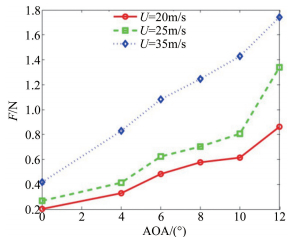
图 9给出了在不同迎角下翼尖涡引起的诱导阻力的变化规律。
|
| 图 9 迎角对翼尖诱导阻力的影响 Fig.9 Induced drag of wingtip influenced by the angle of attack |
图 9中横坐标为机翼迎角,纵坐标为机翼翼尖处的诱导阻力。图中红色实线、绿色虚线和蓝色点画线则分别给出了风速U=20、25和35m/s时翼尖涡引起的诱导阻力的变化曲线。从图中可以看到,不同风速下的翼尖涡引起的诱导阻力随机翼迎角的变化规律一致,均是随着迎角的增大而不断地增大。
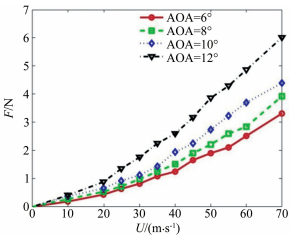
图 10给出了在不同风速下,翼尖涡引起的诱导阻力的变化规律。图中红色实线、绿色虚线、蓝色虚点线以及黑色点画线则分别给出了迎角AOA=6°、8°、10°和12°时翼尖涡引起的诱导阻力的变化曲线。
|
| 图 10 风速对翼尖诱导阻力的影响 Fig.10 Induced drag of wingtip influenced by airflow speed |
图 10中横坐标为风速,纵坐标为机翼翼尖处的诱导阻力。从图中可以看到,不同机翼迎角下的翼尖涡引起的诱导阻力随风速的变化规律一致,均是随着风速的增大而不断地增大,这主要是由于随着风速的增大,翼尖涡不断增强,从而使得翼尖涡与主机翼间的相互作用变大,导致了翼尖处诱导阻力的增大。
3 基于翼尖涡物理特征的诱导阻力减阻机制根据上面的研究,通过3DPIV技术获得了翼尖涡的物理特征,此外,利用传感器测量和计算得到了翼尖处的诱导阻力。基于这2部分的内容将进一步分析研究翼尖涡的物理特征对诱导阻力的影响以及相应的诱导阻力减阻机制。
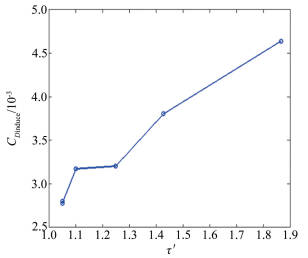
图 11给出了翼尖处的诱导阻力系数CDinduce与翼尖涡的无量纲环量Γ*的关系曲线图。其中,诱导阻力系数CDinduce可表示为:
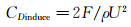 (2)
(2)
|
| 图 11 翼尖涡无量纲环量对诱导阻力系数的影响 Fig.11 Coefficient of induced drag of wingtip influenced by non-dimensional circulation |
式中:F为翼尖处的诱导阻力;U为风洞的风速;ρ为风洞内的空气密度。
图 11中可以看到,机翼翼尖诱导阻力系数随着翼尖涡的无量纲环量Γ*增大而不断地增大。在近壁面处,随着翼尖涡无量纲环量的增大,翼尖涡与主机翼之间的相互作用变强,引起的诱导阻力也会随之增大。即,翼尖处的诱导阻力系数与翼尖涡的无量纲环量呈正相关,即
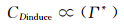 (3)
(3)
由此,与传统的减阻方法相同,翼尖涡的无量纲环量的减小,即抑制翼尖涡的生长也将作为机翼翼尖诱导阻力的减阻目标之一。
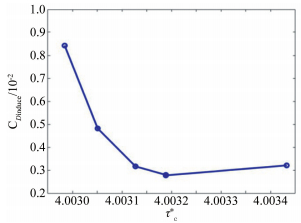
图 12给出了翼尖处的诱导阻力系数CDinduce与翼尖涡与主机翼无量纲距离rc*之间的关系曲线图。rc*为翼尖涡涡核与机翼尾缘翼尖处之间的无量纲距离,可表示为:
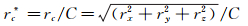 (4)
(4)
|
| 图 12 翼尖涡与主机翼间的距离对诱导阻力系数的影响 Fig.12 Coefficient of induced drag of wingtip influenced by non-dimensional distance between the vortex core and the airfoil |
式中:rc为翼尖涡涡核与机翼尾缘翼尖处之间的距离,如图 4所示。rx、ry和rz为翼尖涡涡核与机翼尾缘翼尖处在3个方向上的距离,C为机翼弦长。
图 12中可以很明显地看到,翼尖处的诱导阻力系数CDinduce随着涡核与主机翼尾缘翼尖处之间的无量纲距离rc*的增加逐渐减小。在近壁面处,随着翼尖涡逐渐靠近主机翼,使得翼尖涡对主机翼造成的下洗作用变强,即翼尖涡与主机翼之间的相互作用变强,从而使得引起的诱导阻力也增大。即翼尖处的诱导阻力系数除了与翼尖涡的无量纲环量呈正相关以外,同时与翼尖涡和主机翼尾缘翼尖处之间的无量纲距离呈反相关,即
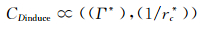 (5)
(5)
除了抑制翼尖涡的强度以外,控制翼尖涡与主机翼之间的距离也将作为机翼翼尖诱导阻力的减阻目标之一。
不过,当翼尖涡与主机翼之间的距离过大时,由于翼尖涡此时远离主机翼,它对诱导阻力系数CDinduce的影响不敏感。那么
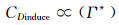 (6)
(6)
因此,在机翼翼尖减阻设计中,可以通过控制和利用Γ*和rc*等翼尖涡的物理特征参数,实现诱导阻力的减阻。具体而言,在进行机翼翼尖减阻时,通过抑制翼尖涡的强度或是控制翼尖涡的运动,改变翼尖涡与主机翼尾缘翼尖处之间的无量纲距离,即减小了翼尖涡与主机翼之间的相互作用,从而实现了机翼翼尖减阻。
4 结论本文通过风洞实验,研究了翼尖涡的物理特征以及机翼诱导阻力的减阻原理。通过对实验结果的分析得到以下的结论:
(1) 实验中利用3DPIV技术拍摄并进行流场处理,得到了翼尖涡的物理特征。通过实验结果表明,翼尖涡的无量纲环量以及涡核的尺寸会随着机翼迎角以及风速的增大而增大。
(2) 基于高精度单分量传感器,作者提出并设计了一套翼尖气动阻力测量实验装置,并根据该实验装置测量得到的气动阻力进行计算求得翼尖涡引起的诱导阻力。
(3) 根据对翼尖涡物理特征以及诱导阻力的分析,得到通过控制和利用Γ*和rc*等翼尖涡的物理特征参数可以实现诱导阻力的减阻。具体而言,在进行机翼翼尖减阻时,通过抑制翼尖涡的强度或是控制翼尖涡的运动,改变翼尖涡与主机翼尾缘翼尖处之间的无量纲距离,即减小了翼尖涡与主机翼之间的相互作用,可以实现机翼翼尖减阻。
| [1] | 马汉东, 崔尔杰. 大型飞机阻力预示与减阻研究[J]. 力学与实践, 2007, 29(2): 1–8. Ma H D, Cui E J. Drag prediction and reduction for civil transportation aircraft[J]. Mechanics in Engineering, 2007, 29(2): 1–8. |
| [2] | Birch D, Lee T. Structure and induced drag of a tip vortex[J]. Journal of Aircraft, 2004, 41(5): 1138–1145. DOI:10.2514/1.2707 |
| [3] | Devenport W J, Rife M C, Liapis S I, et al. The structure and development of a wing-tip vortex[J]. Journal of Fluid Mechanics, 1996, 312: 67–106. DOI:10.1017/S0022112096001929 |
| [4] | 江永泉. 翼梢小翼的空气动力机理[J]. 民用飞机设计与研究, 1993(3): 16–22. |
| [5] | 顾蕴松, 程克明, 郑新军. 翼尖涡流场特性及其控制[J]. 空气动力学学报, 2008, 26(4): 446–451. Gu Y S, Cheng K M, Zheng X J. Flow field characteristics of wing tips vortex and its control[J]. Acta Aerodynamica Sinica, 2008, 26(4): 446–451. |
| [6] | Gatto A, Mattioni F, Friswell M I. Experimental investigation of bistable winglets to enhance wing lift takeoff capability[J]. Journal of Aircraft, 2009, 46(2): 647–655. DOI:10.2514/1.39614 |
| [7] | Sun R M, Daichin. Experimental investigation on tip vortices and aerodynamics[J]. Theoretical and Applied Mechanics Letters, 2011, 1(3): 1–6. |
| [8] | Ashurst W T, Meiburg E. Three-dimensional shear layers via vortex dynamics[J]. J Fluid Mech, 1988, 189: 87–116. DOI:10.1017/S0022112088000928 |
| [9] | Knio O M, Ghoniem A F. Numerical study of a 3-dimensional vortex method[J]. Journal of Computational Physics, 1990, 86(1): 75–106. DOI:10.1016/0021-9991(90)90092-F |
| [10] | Cai J. LES for wing tip vortex around an airfoil[D]. Texas:University of Texas, 2006:74-75. |
| [11] | Lee C S. Flow structure and scaling laws in lateral wing-tip blowing[J]. AIAA J, 1989, 27: 1002–1007. DOI:10.2514/3.10211 |
| [12] | Lee C S, Tavella D. Flow structure of lateral wing-tip blowing[R]. AIAA-1986-1810, 1986. |
| [13] | Margaris P, Gursul I. Effect of steady blowing on wing tip flowfield[R]. AIAA-2004-2619, 2004. |
| [14] | Catalano F M, Ceron-Mufioz H D. Experimental analysis of the aerodynamic characteristics of adaptive multi-winglets[C]. 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno:AIAA, 2005. |
| [15] | Falclio L, Gomes A A, Suleman A. Aero-structural design optimization of a morphing wingtip[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(10): 1113–1124. DOI:10.1177/1045389X11417652 |
| [16] | Boiler C, Kuo C M. Demonstration of adaptive structure performance on modular micro airvehicle[C]. 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando:AIAA, 2010. |
| [17] | Kroo I. Drag due to lift concepts for prediction and reduction[J]. Annual Review of Fluid Mechanics, 2001, 33: 587–617. DOI:10.1146/annurev.fluid.33.1.587 |
| [18] | Chao D D, Dam C P. Wing drag prediction and de-composition[R]. AIAA-2004-5074, 2004. |
| [19] | Ringuette M J, Milano M, Gharib M. Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates[J]. Journal of Fluid Mechanics, 2007, 581: 453–468. DOI:10.1017/S0022112007005976 |
| [20] | Dacles-Mariani J, Kwak D, Zilliac G G. On numerical errors and turbulence modeling in tip vortex flow prediction[J]. International Journal for Numerical Methods in Fluids, 1999, 30: 65–82. DOI:10.1002/(ISSN)1097-0363 |
| [21] | Takahashi R K, Mcalister P K W. Study of a wing-tip vortex using laser velocimetry[R]. NASA-Technical Memorandum-88343, Washington, D. C.:NASA, 1987. |
| [22] | Li J, Cai J, Liu C. Large eddy simulation of wing tip vortex in the near field[R]. Mathematics Preprint Series. The University of Texas at Arlington, 2007. |
| [23] | Bailey S C C, Tavoularis S. Measurements of the velocity field of a wing-tip vortex, wandering in grid turbulence[J]. J Fluid Mech, 2008, 601: 281–315. |
| [24] | Prasad A K, Jensen K. Scheimpflug stereo camera for particle image velocimetry in liquid flows[J]. Appl Opt, 1995, 34: 7092. DOI:10.1364/AO.34.007092 |
| [25] | Jardin T, Farcy A, David L. Three-dimensional effects in hovering flapping flight[J]. J Fluid Mech, 2012, 702: 102–125. DOI:10.1017/jfm.2012.163 |



