随着列车运行速度的提高,列车穿越隧道引起一系列空气动力学效应,进而对周围的环境产生影响[1-3]。当列车高速驶入隧道时,由于空间瞬间变小,前方空气受到挤压,产生压缩波,称之为初始压缩波。初始压缩波以当地声速向隧道出口方向传播,在隧道出口端发生反射,反射波以膨胀波的形式在隧道内反方向向隧道入口传播,另外一部分压缩波由出口端向周围环境以脉冲的形式辐射,形成洞口微气压波[4-6]。
洞口微气压波的能量大部分分布在次声波区[7],即频率在20Hz以下,低于人类听觉下限。但是,某些频率的次声波由于和人体器官的振动频率相近,容易使人体器官产生共振,尤其是高强度的音爆次声波会对隧道周围的环境和人员产生严重的不利影响。列车运行速度越高,列车通过隧道时产生的微气压波的强度就越强。开展隧道压力波和微气压波形成机理的实验研究,对保护隧道口处的环境、保障车内的人员安全和满足舒适性要求的车体设计具有一定的参考价值。
目前隧道压力波和洞口微气压波的研究方法有实车线路试验、动模型实验和数值模拟3种方法。线路试验是最直接可靠的基本试验方法,可获得最符合实际的数据,可以验证计算方法的正确性,但组织实施费用高、测试结果易受环境因素影响且试验条件局限于现有隧道和列车。动模型实验装置是研究列车空气动力学的专用实验平台。在空气中,将列车模型加速到列车的实际运行速度,进而开展相关的空气动力学实验。按加速方式分为弹射式和管道式2类,其中,管道式加速大多采用轴对称列车模型,主要模拟具有相同阻塞比的列车隧道压力波和出口微气压波问题。但由于其尺寸小,结构简单,故不能反映真实隧道结构和列车的三维形状;弹射式加速主要有英国于1991年建成的缩比1:25、最高实验速度305km/h[8]和我国中南大学于1998年建成的缩比1:20、最高实验速度350km/h [9]的动模型实验平台。利用这些实验装置,开展了大量列车隧道压力波和出口微气压波实验研究[10-12]。为了实现更高的实验速度和更接近实际列车运行的雷诺数,笔者利用压缩空气间接加速和磁涡流阻尼力制动列车模型的技术,研制了模型缩比为1:8、最高实验时速可达500km的双向动模型实验平台[13-14]。利用该实验平台,可得到更加接近于实际的隧道压力波和微气压波基础实验数据,校核理论和计算方法,总结压力波和微气压波变化规律。
本文介绍了利用自主研制的动模型实验平台,依据我国双线隧道静空面积100m2的实际隧道图纸和动模型实验段的可用长度,搭建了60m长的双线隧道模型,开展了实验速度在200~350km/h范围内、不同隧道壁面位置的压力波和不同隧道出口位置微气压波的测量研究。首先依据隧道壁面固定测点的压力波数据与列车运行位置及压力波传播和反射过程的关系、不同速度的初始压缩波无量纲曲线及距隧道口一定距离后压力波应该呈现一维平面波的特性,分析测量数据的正确性;在此基础上,总结隧道压力波最大值随实验速度和隧道入口距离因隧道壁面粘性影响的衰减变化规律和隧道出口不同位置微气压幅值随实验速度的变化特性;最后测量2种不同长度流线形头型的列车以相同速度通过同一隧道时的洞口微气压波,研究头型设计对微气压波的影响,对优化列车头型,减小高速列车隧道效应具有参考价值。
1 实验装置高速列车隧道通过实验模拟是在中国科学院力学研究所怀柔基地的双向动模型实验平台上完成的,该实验平台的轨道和隧道模型均是依据我国标准双向轨道5m的中心间距、双线隧道静空面积100m2按缩比1:8搭建的。该平台分为上下2层,上层由列车模型加速段、实验段和减速段3部分组成;下层为拖车加速段、拖车减速段及其活塞的加速管、泄气管和减速管,这里活塞和拖车利用牵引绳连接;加速管端口侧面连接空气炮。实验时,根据实验速度,将压缩空气注入空气炮,空气炮开启时,压缩空气流入加速管推动活塞运动,运动活塞牵引拖车沿下层轨道滑动,同时牵引上层列车模型加速(加速段长50m);加速结束后,拖车进入减速段(由2个竖直设置的平行铁板组成),因拖车两侧布置了强力永久磁铁,当其滑过平行铁板之间会产生磁涡流阻尼力使拖车减速(减速段长度50m),这时活塞已通过泄气段,压缩气体从泄气孔的逃逸使活塞前后压力逐渐平衡,活塞通过牵引索和拖车连接而一起减速,最终停止。当拖车进入减速段时,由于惯性作用,上层的列车模型由于惯性做匀速运动与拖车自动分离,随后基本匀速地滑行通过实验段,完成相关气动测试。在上层减速段,同样采用镶嵌永久强力磁铁的车底滑块与减速段铁板作用产生磁涡流阻尼力使列车模型减速,减速段长度为100m。该平台可以将100kg的列车模型加速到500km/h以上、将260kg的模型加速到400km/h以上。在开展隧道空气动力学实验时,将60m长的隧道模型固定在实验段。隧道截面尺寸如图 1所示,其中可以看到4个压力传感器在其截面上的安装位置。

|
| 图 1 隧道模型截面尺寸 Fig.1 Section dimension of the tunnel model |
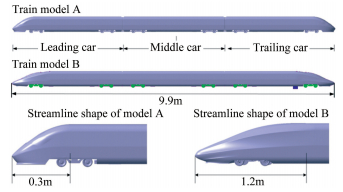
实验模拟中,使用头车、中车、尾车编组的缩比为1:8的2种列车模型,如图 2所示。列车模型长度为9.9m,截面积为0.186m2,但2种头车的外形明显不同,其中模型A的流线型部分的长度为0.3m,模型B为1.2m。列车横截面积和隧道内的横截面积的比值,即隧道阻塞比为β=0.119。隧道模型安装在动模型实验段的实际情况如图 3所示。
|
| 图 2 2种列车模型的结构外形图及其相关尺寸 Fig.2 Streamline shape and dimension of two kinds of train models |

|
| 图 3 隧道模型安装在实验平台上的状态 Fig.3 Installation of the tunnel model on the moving model rig |
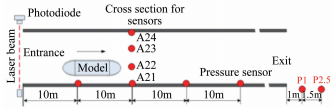
图 4给出了隧道壁面压力波测量传感器安装位置。距隧道入口的距离分别为10、20、30和40m,离地高度471mm处有4个测压传感器(对应A11、A21、A31和A41);距隧道口20m截面的周向有4个测压传感器(对应A21、A22、A23和A24),如图 1所示。微气压波的探测安装在距隧道出口1和2.5m处。其中,隧道壁面测压传感器的量程为7000Pa,微气压波的量程为2000Pa,数据采集系统的采样频率为5kHz,A/D采样精度16位。
|
| 图 4 隧道模型、速度测量装置、内壁面压力波测量和微气压波测量的仪器的相对位置 Fig.4 Positions of the velocity measurement device, the sensors for the tunnel pressure wave and the micro pressure wave at the tunnel model |
在列车模型进入隧道时,利用激光束和光电探测器测量了列车模型的实验速度。利用列车模型A开展了速度分别为202、251、304和344km/h的隧道通过实验,利用列车模型B开展了速度为304km/h的对比实验。在穿越隧道过程中,由于气动阻力和隧道壁面摩擦力的作用,列车模型的速度略有下降,大约在3%左右,因此可以认为列车模型是匀速运动。下面介绍列车模型在穿越隧道过程中,隧道压力波的变化特征、在隧道出口处的微气压波特征及其流线型长度对隧道压力波和微气压波的影响。
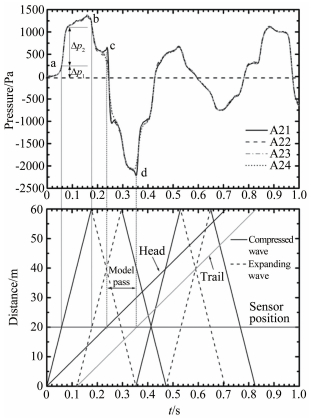
2.1 隧道压力波实验结果有效性分析图 5(a)给出了列车模型A以速度304km/h穿越隧道,距隧道入口20m的隧道壁面4个测点的压力波时程曲线(对应A21、A22、A23和A24)。为了分析列车通过隧道的过程,图 5(b)给出了对应的压力波传播和列车模型运行轨迹及其与图 5(a)的对应关系。在图 5(b)中,倾斜的黑实线表示压缩波的传播轨迹,倾斜的虚线表示膨胀波的传播轨迹,两者均以声速传播;同时给出了车头和车尾的运行轨迹。
|
| 图 5 (a) 距隧道入口20m处隧道截面不同位置的内壁面压力演化过程; (b)对应的马赫波传播图,这里模型的时速为304km/h Fig.5 (a) Pressure evolution on the inner wall of the tunnel model at 20m from the entrance and (b) Mach wave propagation in the case of 304km/h |
由图 5(a)可以看出,列车在进入隧道之前,隧道内的空气已经受到干扰,产生小幅度的压力波动,传播至测点,导致压力增加,即Δp1。接着,列车车头的变截面鼻锥区进入隧道(a点对应的时刻),产生压缩波传播至测点,测点压力剧烈增加,即Δp2。在列车进入隧道的过程中,列车的阻塞作用逐渐显现,测点压力继续逐渐增加,直至全部车身进入隧道。当列车尾部进入隧道时,产生的膨胀波通过该测点时,才导致压力开始下降,即b点。因此,压力波动曲线a到b段即为初始压缩波。压力波动的c到d段为列车通过该测点,列车车头在经过时会引起一个短暂的压力上升,然后使压力突然降低,列车车尾经过后,压力再逐渐上升;随后的过程是压缩波传播至出口,反射后成为膨胀波,而原来的膨胀波传播至出口反射后转换为压缩波。进一步的分析表明,压缩波传播至测点时,压力通常呈增加的趋势,而膨胀波经过测点时,压力通常呈下降的趋势。总之,测量的压力波波峰、波谷和转折点与压力波解析传播图一一对应,反映测量结果变化趋势是正确的。
另一方面,当列车在隧道内运行时,距隧道入口20m处的横截面4个位置处的压力波曲线基本重合,只是在列车车头经过该横截面时,靠近列车车头壁面的测点会受到列车车头前方高压区的影响大(A21),而远离列车车头的一侧则受到的影响比较小。同样,在列车车尾经过时,约在靠近列车车尾一侧隧道壁面有较小的压力下降,导致隧道压力波负峰值靠近车尾一侧为-2217.5Pa,远离车尾一侧为-2089.2Pa,幅值相差6%。总之,同一隧道截面不同点压力波特性基本一致,与距隧道入口一定距离后压力波呈现一维平面波特性,与文献[15-17]研究结果一致,进一步反映测量结果的有效性。
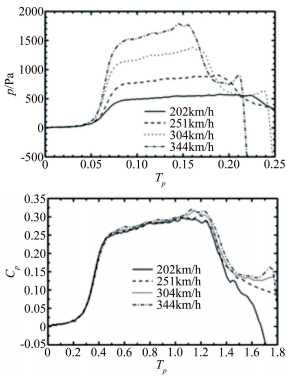
图 6(a)给出距入口20m处测点在不同速度下初始压缩波变化曲线。随着列车通过隧道的速度增大,初始压缩波的幅值逐渐增加。
|
| 图 6 4种速度下(a)隧道压力波的初始阶段和(b)无量纲处理的结果 Fig.6 (a) Initial stage of the compressed wave in the case of 4 speed values and (b) corresponding curves for the non-dimensional process |
引入如下的时间和压力的无量纲化系数Tp和Cp
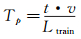 (1a)
(1a)
 (1b)
(1b)
式中:p是测得的气动压力,Pa;ρ为空气的密度,kg/m3 (取值1.225);v是列车运行速度,m/s。图 6(b)给出了对应的无量纲化处理结果。实验速度的无量纲压力波在初始发展阶段基本一致,反映不同速度的压力波测量结果是有效的。
通过对压力波时程曲线与传播特性对应关系、距隧道入口一定距离隧道壁面不同位置测点的压力波曲线比较和同一测点不同速度的压力波无量纲对比,可以判断动模型实验测量结果是有效的。下面利用这些结果开展进一步的分析。
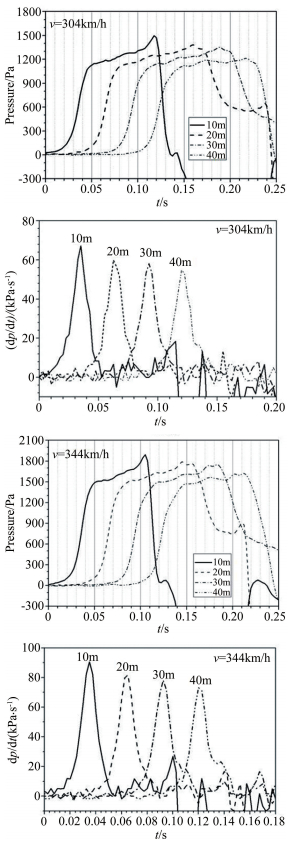
2.2 隧道压力波衰减特性分析图 7(a)和(b)分别给出了304和344km/h 2种速度下距隧道入口不同距离的4个隧道壁面测点的压缩波时程变化曲线及其压力梯度的比较。可见,压缩波在隧道内传播过程中,由于隧道壁面粘性作用,初始压力波强度及其梯度随距隧道入口距离增加略微衰减。图 8显示了该4个实验速度下,4个测点压力波最大值随隧道入口距离的衰减变化情况。可以看到:速度越高,随着距隧道入口距离的增加,对应的压力衰减值越大,202km/h速度下从657.87Pa降低到476.63Pa,344km/h速度下从1892.1Pa降低到1622.99Pa;但衰减斜率基本一致,也就是说,对60m长的实验隧道,在实验速度200~350km/h范围内,不会出现压力波传播非线性传播效应,基于单一速度的压力波无量纲值可以转换为其他速度的压力波时程曲线。
|
| 图 7 4个位置的初始压缩波及其压力梯度随时间的演化:(a)304km/h和(b) 344km/h Fig.7 Initial stage of the compressed waves and pressure gradients at 4 positions in the case of (a) 304km/h and (b) 344km/h |
|
| 图 8 不同速度下隧道压力波的最大值及无量纲化压力系数 Fig.8 Maxima of the compressed wave for several speeds |
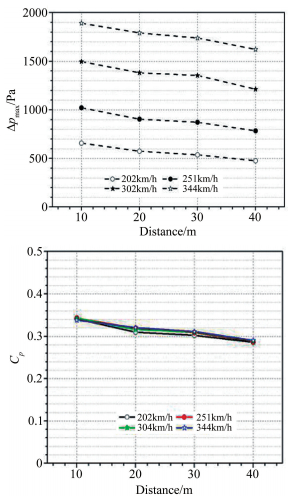
列车进入隧道产生的初始压缩波在隧道内传播到达隧道端口时向外辐射,形成洞口微气压波。图 9给出了列车以304km/h通过隧道距隧道出口2.5m处的压力波动曲线及对应的压力波传播和列车运行轨迹图。在M1时刻,列车进入隧道产生的初始压缩波向洞口向外辐射,刚好传播到该测点;M2和M3分别为尾车产生的膨胀波和初始压缩波经二次折射到该测点的对应时刻,随后,列车驶出隧道,当头车经过该测点时,产生先升后降的压力波动,尾车经过测点引起的波动与头车相反,产生先降后升的压力波动。
|
| 图 9 距隧道模型出口2.5m处的微气压波演化曲线,这里列车模型速度为304km/hour Fig.9 Evolution of the micro pressure wave at the position of 2.5m from the exit of the tunnel model in the case of 304km/h |
图 10给出了列车模型A以不同速度通过隧道时,对应洞口1和2.5m位置的微气压波幅值变化曲线。随着速度的增加,微气压波幅值增加,幂级数拟合结果可以看出与实验模型速度的3次方成正比,符合理论分析,但两者的变化斜率不一致,这也许是微气压波以球面波向隧道出口外传播、2个测点不是安装在同一径向方向上的原因。
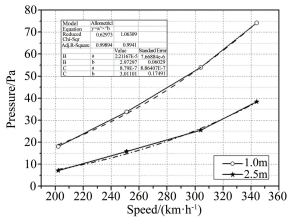
|
| 图 10 4种速度下模型A在隧道出口1和2.5m处的微气压波的峰值 Fig.10 Dependence of the peak values of the micro pressure waves atthe positions of 1m and 2.5m from the exit on the speed of train model |
在隧道长度和列车长度给定的情况下,微气压波主要取决于隧道阻塞比,同时流线型头型也对微气压波有一定影响。图 11(a)和(b)给出了图 1所示的A和B这2种头型的列车模型在相同速度304km/h下隧道通过对应的20m隧道壁面和隧道出口外1m处的压力波和微气压波波形比较。模型A的流线型长度较短,初始压力波和微气压波幅值较大,模型B的流线型长度较长,初始压力波和微气压波幅值较小。具体来说,模型A的微气压波幅值为55.92Pa,模型B的微气压波幅值为47.42Pa,模型A的值高出模型B约17.9%。由于实验数据有限,很难总结出其他条件一致时微气压波幅值与头型流线型长度的定量关系。为降低隧道内压力波和隧道出口微气压波幅值,建议在结构条件允许的条件下,尽可能增加列车头型的流线形长度。
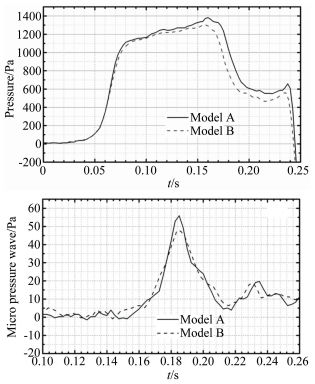
|
| 图 11 在时速为304km/h运行时,2种模型的(a)隧道内的A21位置处的初始压力波波形和(b)隧道出口1m处对应车头进入隧道时的微气压波波形 Fig.11 Initial stage of the compressed wave at the position of A21 for two kinds of train models in the case of 304km/h and (b) the curves of the micro pressure wave at the position of 1m from the exit |
本文利用缩比为1:8的高速列车动模型实验平台和60m长的隧道模型,采用头、中、尾3编组列车模型和隧道模型内多个位置安装的高频压力传感器,开展了在列车通过隧道过程中的隧道内壁压力波动和出口微气压波的模拟测量研究。实验结果表明:(1) 列车进入隧道时,隧道内壁各点压力的上升和下降与车头和车尾进入隧道时产生的压缩波和膨胀波及其以声速传播至隧道出口后的两者之间的相互转换有关。通常压缩波经过后,壁面各点压力开始上升;膨胀波经过后,压力开始下降,且隧道截面上不同点位的压力变化基本等幅和同步。(2) 壁面各点压力上升和下降的幅度与列车的速度成正比,且压力变化幅度随着到进口距离的增加而线性地减小。(3) 在隧道出口,产生微气压波。在头车经过时,压力先升后降;尾车经过时,压力先降后升;且波动幅度随着距隧道出口距离的增加而减小。(4) 列车头部的鼻锥越长,隧道内压力波动的幅度和隧道口微气压波的强度就越小。
| [1] | 杨国伟, 魏宇杰, 赵桂林, 等. 高速列车的关键力学问题[J]. 力学进展, 2015, 45: 201507. Yang G W, Wei Y J, Zhao G L, et al. Research progress on the mechanics of high speed rails[J]. Advances in Mechanics, 2015, 45: 201507. DOI:10.6052/1000-0992-14-002 |
| [2] | Yoon T S, Lee S, Hwang J H, et al. Prediction and validation on the sonic boom by a high-speed train entering a tunnel[J]. Journal of Sound and Vibration, 2001, 247(2): 195–211. DOI:10.1006/jsvi.2000.3482 |
| [3] | Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38: 469–514. DOI:10.1016/S0376-0421(02)00029-5 |
| [4] | 马伟斌, 张千里, 程爱君, 等. 高速铁路隧道洞口微气压波影响因素与变化规律研究[J]. 铁道学报, 2013(5): 97–102. Ma W B, Zhang Q L, Cheng A J, et al. Study on influence factors and changing law of micro-pressure waves at tunnel portals of high-speed railways[J]. Journal of the China Railway Society, 2013(5): 97–102. |
| [5] | Howe M S. Review of the theory of the compression wave generated when a high-speed train enters a tunnel[C]//Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 1999, 213(2):89-104. |
| [6] | Auvity B, Bellenoue M, Kageyama T. Experimental study of the unsteady aerodynamic field outside a tunnel during a train entry[J]. Experiments in Fluids, 2001, 30(2): 221–228. DOI:10.1007/s003480000159 |
| [7] | 杨志刚, 谭晓明, 梁习锋, 等. 高速列车过隧气压爆波的声学特征与传感器选型[J]. 中南大学学报(自然科学版), 2014, 45: 1329–1333. Yang Z G, Tan X M, Liang X F, et al. Acoustical characteristics of micro-pressure wave and sensor selection[J]. Journal of Central South University Science and Technology, 2014, 45: 1329–1333. |
| [8] | Johnson T, Dalley S. 1/25 scale moving model tests for the TRANSAERO Project[M]. Berlin Heidelberg:Springer, 2002. |
| [9] | Zhou D, Tian H, Zhang J, et al. Pressure transients induced by a high-speed train passing through a station[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135: 1–9. DOI:10.1016/j.jweia.2014.09.006 |
| [10] | Bellenoue M, Moriniere V, Kageyama T. Experimental 3-D simulation of the compression wave, due to train-tunnel entry[J]. Journal of Fluids and Structures, 2002, 16(5): 581–595. DOI:10.1006/jfls.2002.0444 |
| [11] | Ricco P, Baron A, Molteni P. Nature of pressure waves induced by a high-speed train travelling through a tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 781–808. DOI:10.1016/j.jweia.2007.01.008 |
| [12] | Doi T, Ogawa T, Masubuchi T, et al. Development of an experimental facility for measuring pressure waves generated by high-speed trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(1): 55–61. DOI:10.1016/j.jweia.2009.09.002 |
| [13] | Yang Q S, Song J H, Li D, et al. Train model acceleration and deceleration[J]. Science China Technological Sciences, 2013, 56(3): 642–647. DOI:10.1007/s11431-012-5101-5 |
| [14] | Yang Q S, Song J H, Yang G W. A moving model rig with a scale ratio of 1/8 for high speed train aerodynamics[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 152: 50–58. DOI:10.1016/j.jweia.2016.03.002 |
| [15] | 梅元贵, 周朝辉, 耿烽, 等. 高速铁路隧道初始压缩波一维流动模型的数值分析方法[J]. 空气动力学学报, 2006, 24(4): 508–512, 519. Mei Y G, Zhou C H, Geng F, et al. Numerical method of initial compression waves produced by a high-speed train entering a tunnel-hood based on one dimensional unsteady compressible flow model[J]. Acta Aerodynamica Sinica, 2006, 24(4): 508–512, 519. |
| [16] | Takayama K, Sasoh A, Onodera O, et al. Experimental investigation on tunnel sonic boom[J]. Shock Waves, 1995, 5(3): 127–138. DOI:10.1007/BF01435520 |
| [17] | Ozawa S, Maeda T, Matsumura T, et al. Countermeasures to reduce micro-pressure waves radiating from exits of Shinkansen tunnels[C]//Proceedings of the Seventh International Conference on the Aerodynamics and Ventilation of Vehicle Tunnels, Brighton, UK, 1991:253-266. |



