液膜流动是一种常见的低速开放式流动,它蕴涵着极其丰富的动力学行为,其中的交界面不稳定性、自由表面波、三维时空图像等非线性现象一直是流体力学工作者所研究的热点[1]。在工业上也具有广泛的应用和研究,比如涂布流、降膜反应器、薄膜传热与蒸发冷凝等等,甚至填料塔、圆盘反应器、微流体反应器等都可以用液膜流动理论来强化传质反应过程。根据液膜形成特征可以分为壁面膜(一侧有固体壁面支撑,仅有1个自由面)和自由膜(在流动过程中不接触任何固体,同时拥有2个自由面)[2]。关于壁面膜,自Kapitza父子[3]开创倾斜板上的薄膜下落实验后,许多学者通过不同的测试设备和数值计算方法开展这类研究,发现了孤立波、三维不稳定性、回流等特殊流动现象。Wasden和Dukler[4]通过数值计算发现液膜波动会使垂直于膜厚方向速度分量增加,有效促进传质过程。Alekseenko et al.[5]、Chang和Demekhin[6]以及Kalliadasis et al.[7]对液膜流动的实验方法、稳定性分析、数值计算等方面进行了系统阐述。关于自由膜,由于2个自由面的存在,在改变液体流量或物性时会出现如液滴、液柱、液膜等一系列丰富流型。对它的研究主要集中在液膜波动的稳定性与射流破裂,其理论在发动机燃烧和喷雾领域等有着重要作用。Squire[8]较早通过理论和实验分析了静止气体中自由液膜的稳定性以及射流破裂问题。Brown[9]测定了自由下落液膜的速度分布,发现对于低黏液体,液膜速度接近于自由落体变化,并初步提出维持液膜稳定的韦伯数(We)准则。Lin和Robert[10]通过在自由液膜中心放置一小障碍物,发现自由膜受扰时波动会产生2种不同的形式,一类是非对称的曲波,一类是对称的膨胀波。随后更多学者不断对相关理论、模型进行改进,更加详细的著作可以参见Lin[11],Sirignano与Mehring[12]。此外也有部分学者研究了下降自由膜的流型随流量的变化[13]。
对于2类液膜的研究,至今逾半个世纪,然由于各自不同的工业应用背景和研究角度,对两者的研究甚少关联。尤其是自由膜,其流动更加复杂,研究相对较少,主要集中在稳定性分析而缺少传质等方面的研究。而事实上,在现有化工设备中,如散堆填料和规整填料、圆盘反应器等,往往在固体壁面上开有大小不一的孔或窗,并非完整的壁面或完全的自由空间。当液体完全覆盖在这样的开窗板上时,即会形成板上壁面膜与窗口区受限自由膜交替共存的现象(可称之为孪生液膜),呈现出不同于两者的新流动特性。更值得一提的是,不少工业设备如填料塔,早期的经典理论都是在壁面膜基础上建立并沿用至今,然而随着时间的发展,壁面开孔已成一种趋势[14],传统的理论及模型已不再完全适用。虽然部分学者发现开孔后填料塔内的传质及流动通量有所改变[15-17],但国内外文献均未见对窗口区的液膜流动进行报道。
此外,现有的工业设备,从填料片上几毫米的小孔到大型圆盘反应器数米的开窗,其形状和尺寸都相差巨大,但在工业实践中尚无明确统一的指导理论。目前的认知表明,当窗口尺寸小于毛细长度时整个孪生液膜的性能更接近壁面膜(孔内会形成液桥和死区而不再体现自由液膜的流动特征);当窗口尺寸远大于毛细长度时,在重力加速作用下,窗内液体流动更接近自由液膜(实际上通常对自由液膜的研究中,为了防止液膜收缩,两侧都有铁棒等固体壁面作为支撑)。因而中间尺度的开窗恰恰能最好地体现出孪生液膜的流动特征,也是本文的重点研究对象。最近,Nikolai Kolev等[18]开发了一种由横向条片组成的高性能填料(实则为开有若干矩形窗的平板),实验结果表明此种填料有效比表面积大于1,十分适用于低液体流量下的吸收过程。同时期,Hu等[19-21]开发了一种适用于粘性吸收剂的垂直板填料。与前者不同,Hu等强调板上要开有足够面积的窗口,使无壁支承的自由膜与壁面膜共存,且相互作用。实验结果表明,在一定操作范围内,此种填料相比于商业波纹填料传质效率更高,操作压降更低,操作通量更大。值得注意的是这两者的开窗尺寸都在厘米级,大于常见液体的毛细长度,但又小于通常自由液膜的研究尺寸。
本文在从事液膜相关工作基础上,提出孪生液膜这一新概念。即壁面膜与受限自由膜同时存在、相互作用,形成时互为前驱[19]。此处所谓受限自由膜是指自由面为封闭界面限定,区别于已有广泛研究的无界自由膜。这一概念的提出,既丰富了传统的液膜流动概念,也因其本身已经存在于工业实际,对它的理论研究将有助于这类工业设备的开发和效率提升,亦可进一步为传热、传质设备提供强化手段。王良生等[22]在对聚酯开窗圆盘反应器的研究中,较早注意到窗口区液膜的形成机理与壁面液膜完全不同。随后在其基础上,邓斌等[23]通过数值模拟发现窗口区液膜的表面更新速率要比壁面液膜的高出近40%。但是两者均未对窗口区液膜形成及其特征进行详细分析。Hu等[24]最早通过VOF方法模拟分析了二维开窗区受限自由液膜的部分流动特性,但亦未论述它的形成条件。本文将在前期工作的基础上,展现窗口区丰富多样的流型,并系统地分析物性和窗口形状对窗口区成膜性的影响。本文结构如下:首先阐述实验设备和观测方法,其次考察窗口区的各种流型,最后标度分析流动的特征量并给出窗口区成膜条件的经验判别式。
1 实验设备与过程图 1是测试装置示意图,主要由高位槽、液体流量计、水泵、液体分布器、测试板及液体收集槽、高速摄影仪等组成。实验在常压下进行,液体由泵输送至高位槽,经转子流量计调节流量,在重力作用下从高位槽流至分布器。分布器出口为宽150mm的15°倾斜板,测试板经夹具垂直固定在金属架上。仔细调整两者的间隙后,液体经斜板导流能够均匀铺展于测试板上,最终回到下方水箱。为了准确记录实验过程中的流动现象,采用美国York-Tech公司的Phantom V 9.1高速摄影机,拍摄速率为100~1000帧/s,使用配套软件Phantom Video Player对录像进行后处理。
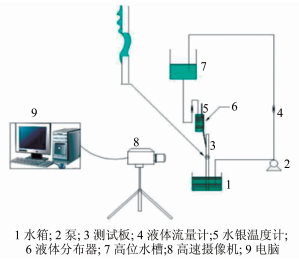
|
| 图 1 实验装置图 Fig.1 Experimental setup |
测试板为200mm×200mm光滑铝板,开窗区距离液体入口约80mm(见图 2)。为了方便叙述,与液膜流动方向垂直的窗边定义为迎流边(长度L),与液膜流动方向平行的窗边定义为流向边(长度W)。为保证液体在窗上方呈均匀液膜流动,采用细砂纸对铝板表面轻微打磨,并用丙酮溶液仔细擦洗以改善其润湿性,同时在每次试验之前进行预润湿。采用日本三丰SJ-201表面粗糙度测试仪,测得打磨后铝板表面的粗糙度为Ra=0.4μm,而本文研究的液膜膜厚均大于100μm且为层流工况,因此可以判定对液膜主体流动的影响可以忽略。

|
| 图 2 测试板 Fig.2 Test plate |
为了考察不同物性对窗口区成膜流量的影响,测试了表 1所示6种液体。其中密度使用50ml容量瓶以称重法获得;粘度测量采用美国TA公司(TA Instruments Inc.New Castle. DE.USA)生产的ARES高级流变仪测得,测量精度为±0.1mPa·s;液体表面张力由上海中晨数字技术设备有限公司(Shanghai Zhongchen Technic Apparatus Co.Ltd)生产的JK99C型全自动张力仪测得,测量精度为±0.01mN/m。实验前后重复测量,整体物性参数的误差约为5%。
| Ka | 密度 ρ/(kg·m-3) |
黏度 μ/(N·s·m-2) |
表面张力 σ/(N·m-1) |
|
| 68%甘油水溶液 | 52.7 | 1160 | 0.0175 | 0.058 |
| 63%甘油水溶液 | 127 | 1150 | 0.0090 | 0.057 |
| 55%甘油水溶液 | 295 | 1110 | 0.0046 | 0.055 |
| 63%酒精溶液 | 406 | 880 | 0.0014 | 0.037 |
| 无水乙醇 | 670 | 790 | 0.0027 | 0.030 |
| 去离子水 | 2.93×103 | 1000 | 0.00098 | 0.072 |
表中: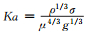 ,g为重力加速度 ,g为重力加速度 |
||||
观察表明液体在窗口区的流动(见图 3)可分为: (1) 绕流:液体绕过窗口边缘,窗下方为“干区”; (2) 偏流:少量液体进入窗区两角,大部分液体绕过边缘,窗下仍为干区; (3) 过流:液体越过窗上边缘进入窗区,并润湿窗下方壁面; (4) 背流:液体偏流、过流时会有少量液体进入板的另一侧。
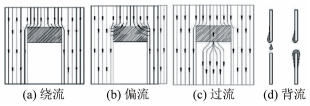
|
| 图 3 窗口区的基本流型示意图 Fig.3 Basic flow patterns around the window region |
上述基本流型的形成主要取决于表面张力、惯性力、重力和黏性力间的平衡。窗口上游均匀液膜向下铺展,在达到窗口上边缘时,会在窗口上沿受到表面张力的阻滞作用。图中,γsv、γsl、γlv分别为气固、固液、气液界面张力,θ为动态接触角(前进角)。固体壁面上液体的铺展,γsv=γsl+γlvcosθ(见图 4(a)),与此不同,在开窗区,窗口上边缘界面张力明显构成了一个与流动方向相反的力γsl+γlvcosθ(见图 4(b)),从而液体进入到窗口区受阻,液体堆积。Oliver[25]等人通过实验对锐角边缘的单液滴移动接触线进行了定量化的研究。结果表明,随着液滴体积的增大,θ会不断增大以维持重力与界面张力的稳定,当θ大于临界值时(具体量值受到物性、接触角和锐角大小等多重参数的影响),接触线才会突越过锐角边缘。本文中,液体跨过开窗区同样需要达到临界能量或流量,来迫使液体进入到窗区。
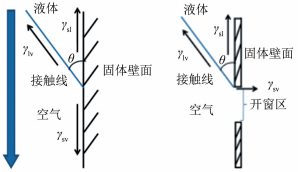
|
| 图 4 壁面(a)和窗口区(b)移动接触线示意图 Fig.4 Sketch of moving contact line on the wall (a) and up the window (b) |
当惯性力和重力克服界面张力后,液体才能进入到窗口区。由于不存在壁面的剪切和黏附作用,此时的流动和成膜机理更多地显现出自由膜的特征。但又与通常自由膜不同:上下游壁面液膜和窗口内的自由膜(假定已经成膜,实际上成膜前有复杂的流型演变,下详)存在流动的连续性和相互干扰;窗上下左右壁面限定自由膜,会对自由膜流动产生直接作用,如液体在窗口区经重力作用加速后会撞击到下壁面;开窗后,壁面两侧连通,增强了液体在膜厚方向上的流动。
对窗区表面张力作用初步分析可知:(1) 当液体的惯性力不足以克服表面张力时,则会类似于局部驻点压力形成绕流;(2) 少量液体进入到窗区,由于接触到左或右侧壁面(壁面液膜),在表面张力的作用下迅速被拉离窗口区,即偏流;(3) 上游液体进入到窗口区后,在表面张力作用下急剧收缩,在接触到下壁面后又会重新铺展开,即过流;(4) 由于横向γsv的作用,以及偏流、过流时液体在板两侧的重新分配,少量液体会进入到板的另一侧,即背流。
2.2 过流流型演变如图 5所示,对给定窗区几何和相应物系,液体越过窗区流型随流量变化,以Re表征(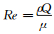

|
| 图 5 不同流量下窗口区的部分流型图(介质为水) Fig.5 Flow patterns in the window (L=48mm, W=12mm) with different Re (water) |
(1) 单滴形成:当流量特别小时,窗口上沿形成了一段厚的液层,类似于局部驻点压力,上游液体会以绕流的形式从窗口区两侧流走。随着流量的增大,液层不断增厚。当Re达到13.9时,可以发现窗口上沿中部的厚液层开始进入到窗口区,并在重力作用下不断积累下落,最终带动周围液体以液桥的形式通过窗口区并润湿窗下游的壁面。随后,液桥在表面张力的拉伸下迅速断裂,回复到液层积累的初始状态,形成一个周期性的过流过程。
(2) 滴柱共存:随着流量的逐渐增大,液滴下落的频率加快,并逐渐转变为稳定的液柱。与此同时迎流边上的液滴落点也将会不断增加,类似于圆环和圆柱上的液柱[26],窗口区的落点之间也存在着临界距离,此处约为10mm。随着落点数量的饱和,窗口区的流动开始出现不规则和随机性。由于开窗区不存在强的黏性剪切,表面张力成为控制液体流动的主导作用。液柱在轻微扰动下就会相互碰撞和聚并,靠近窗两侧的自由膜还能直接以偏流的形式被壁面液膜带走。当Re达到111时,窗口区的流动又重新达到一个稳定的状态,液体以4条液柱的形式穿过窗口区。
(3) 挂膜阶段:进一步增大流量后Re=125,液柱聚并成股,窗口区的流动重新变得不规则。值得注意的是上游液膜的前锋不再限于壁面厚液层区,而是挂在了窗口上沿下方,此时惯性力加上重力与表面张力在窗口区达成了微妙的平衡。由于水具有极高的Ka数,在自然扰动下就能形成小的毛细波。实验过程中发现当上游毛细波达到窗口区时,惯性力就能暂时性地克服表面张力的约束,大量的液体以片状形式进入到窗口区。由于此时流量尚低,液体无法铺满窗口区,在两侧和下方局部表面张力的作用下,不完整的液膜很快就断裂消失。这一阶段是窗口成膜的必经阶段。
(4) 成膜阶段:之后随着流量的增加,进入到窗口的前驱液膜越来越逼近下壁面(如Re=153,窗口区的前驱液膜甚至能覆盖窗口的大半),并在重力、惯性力与表面张力的共同作用下快速收缩和拉伸。直到流量继续增大,或者某一瞬间的扰动使得前驱液膜完全与下壁面贴合,从而形成一个稳定的力平衡。如图所示,Re=158完整的受限自由膜会展现出一个相对稳定并十分规整的波列结构。
通过上述观察,可以发现窗口区液膜流动是在惯性力、表面张力、粘性力和重力共同作用的结果。只有在足够大流量下,惯性力和重力才能克服液体的表面张力进入到窗口区。与此同时,粘性力则能在一定程度上抑制扰动的传播和自由液体表面的不规则运动,促进液体呈膜状接触到下壁面,最终形成完整的液膜。值得注意的是,即使没有成膜,液体在流经窗口区的同时也将发生自由表面的收缩与接触到下壁面时的再铺展,这一过程对工业上的传质及混合都将十分有利。
在进一步考察了其他不同尺寸的窗口(3mm×3mm~48mm×24mm)后,发现:当迎流边长小于10mm时,液体无法以液滴或液柱的形式穿过窗口区,而是从绕流直接跳到挂膜阶段(这是因为液体穿过开窗区需要一定能量积累,当迎流边长和流量较小时,绕流所需的能量要小于前者,因而液体选择绕流);而对于迎流边长较大的窗口,过流时的液柱则会断裂成液滴撞击下壁面;窗尺寸越小其形成的受限自由液膜越稳定。在形成受限自由膜后,即使逐渐减小液体流量,依旧能维持液膜不破裂。直到某一临界值(此窗口Re≈30),液膜瞬间破裂,窗口回复到液滴过流的状态。不同的转变Re和转变流型说明了窗口区成膜和破膜过程存在迟滞现象,两者是不可逆的。这是因为成膜过程中主要是克服表面张力将液体铺展开,而一旦成膜后表面张力达到了平衡就不需要额外的力去维持。Brown[9]曾提出一个判断自由液膜稳定性的We数准则: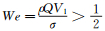
在进一步讨论之前,先对流动的特征量进行简单的标度分析。以液相特征速度Vl和特征长度Ll为基础,导出惯性力Fli、粘性力Flv、重力Flg和表面张力Fls的表达式:
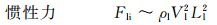 (1)
(1)
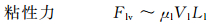 (2)
(2)
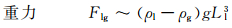 (3)
(3)
 (4)
(4)
在给定Re数(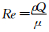
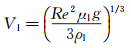 (5)
(5)
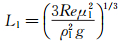 (6)
(6)
再将式(2)~(4) 分别除以式(1) 可以得到如下无量纲式:
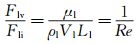 (7)
(7)
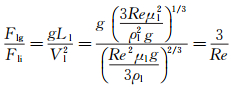 (8)
(8)
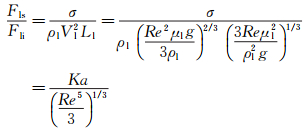 (9)
(9)
从上述分析可以发现影响整个流动工况的主要是Re和Ka这2个无量纲数,而表面张力的作用最为明显(实验范围Ka:52.7~2.93×103,临界成膜Re:4~140)。式(7)~(9) 也在一定程度上解释了为什么Ka,KF=Ka-3[27]以及Ga=Ka3[28]会经常用来关联流型转变的Re。同时为了表征窗几何形状对成膜流量的影响引入无量纲数Nx(L,W),得到了如下形式的经验关联式:
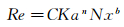 (10)
(10)
式中:C、n、b为待定常数。
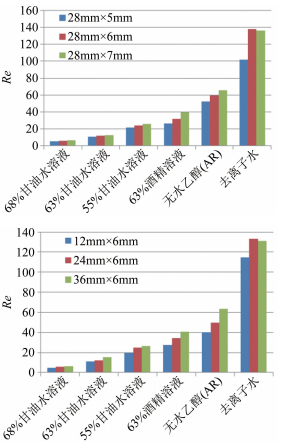
2.4 成膜条件关联式拟合在液膜研究领域中,大量文献关注液膜的流动规律,着眼于液膜形成的很少。本文重点研究了受限自由膜的形成条件。图 6展示了不同矩形窗和不同物性条件下的窗口区临界成膜流量。可以发现,随着迎流边长、流向边长以及Ka数的增加,临界成膜Re不断增加。经拟合得到经验关联式:
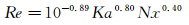 (11)
(11)
或者
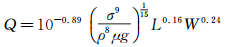 (12)
(12)
式中:Ka:52.7~2.93×103,Nx:2.5~7.1,Re:4~140,平均偏差8.4%。Nx为矩形窗几何的无量纲数: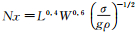
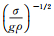
|
| 图 6 不同矩形窗和物性下的成膜Re数 Fig.6 Critical film formation Re with different windows and fluids |
上述关联式在一定程度上反应了成膜过程主要是液膜惯性力和重力克服表面张力向下铺展的过程,而窗迎流长度和流向长度的增加会延长这一铺展过程同时降低成膜过程的稳定性,黏性力则在一定程度上抑制液膜的不稳定性,有利于成膜。因此成膜流量随液体表面张力系数和窗尺寸的增大而增大,随密度和黏度的增高而减小。当然由于成膜过程十分复杂,迎流边(L)与流向边(W)发挥着各自不同的作用,上式中窗几何参数Nx的模型过于简化,因此还存在一定局限性。
3 结论本文通过实验观测对垂直板开窗区的液膜流动行为及其成膜性进行了系统的研究。得到结论:
(1) 下降液膜在通过开窗区时有绕流、过流、偏流和“背流”4种基本流型。对于过流,随着流量的变化,窗口内会出现单液滴、多液滴、单一或多重液柱、液膜以及它们的组合,即多种型态共存、破裂、转变。显然,窗口区受限自由膜的流型具有多样性和动态性的特征。
(2) 本文研究了不同物性、不同矩形窗条件下的受限自由膜成膜流量,并经过标度分析拟合得到了成膜条件的经验判别式。结果表明,临界成膜Re数随着窗迎流边长、流向边长和Ka数的增大而增大,Ka数更为敏感。
(3) 成膜后,开窗板上会呈现壁面液膜与窗内受限自由液膜交替共存(孪生液膜)的特殊流动工况。窗口区受限自由膜特殊的波列结构,开窗后板两侧流体的连通,流体在窗区的重力加速、对窗下壁面的撞击,特别是壁面膜与自由膜的相互作用(即流量波动或扰动下,多种流型的收缩破裂、动态演变)等导致的多重干扰,将会强化全板上的液膜表面更新与液膜波动和湍动。
| [1] | 胡军, 胡国辉, 孙德军. 沿平板下落薄膜流动的研究综述[J]. 力学进展, 2005, 35(2): 161–169. Hu J, Hu G H, Sun D J. A review on thin films falling along an inclined plate[J]. Advances in Mechanics, 2005, 35(2): 161–169. DOI:10.6052/1000-0992-2005-2-J2004-109 |
| [2] | Batchelor G K, Moffatt H K, Worster M. Perspectives in fluid dynamics:a collective introduction to current research[M]. Cambridge: Cambridge University Press, 2002. |
| [3] | Kapitza P. Dynamic stability of the pendulum with vibrating suspension point[J]. Soviet Physics-JETP, 1951, 21(5): 588–597. |
| [4] | Wasden F K, Dukler A E. A numerical study of mass transfer in free falling wavy films[J]. American Institute of Chemical Engineers Journal, 1990, 36(9): 1379–1390. DOI:10.1002/(ISSN)1547-5905 |
| [5] | Alekseenko S, Nakoryakov V E, Pokusaev B G. Wave flow of liquid films[M]. New York: Begell House, 1994. |
| [6] | Chang H-H, Demekhin E A. Complex wave dynamics on thin films[M]. Elsevier, 2002. |
| [7] | Kalliadasis S, Ruyer-Quil C, Scheid B, et al. Falling liquid films[M]. Springer Science & Business Media, 2011. |
| [8] | Squire H B. Investigation of the instability of a moving liquid film[J]. British Journal of Applied Physics, 1953, 4(6): 167–169. DOI:10.1088/0508-3443/4/6/302 |
| [9] | Brown D. A study of the behaviour of a thin sheet of moving liquid[J]. Journal of Fluid Mechanics, 1961, 10(2): 297–305. DOI:10.1017/S002211206100024X |
| [10] | Lin S, Roberts G. Waves in a viscous liquid curtain[J]. Journal of Fluid Mechanics, 1981, 112: 443–458. DOI:10.1017/S0022112081000505 |
| [11] | Lin S P. Breakup of liquid sheets and jets[M]. England: Cambridge University Press Cambridge, England, 2003. |
| [12] | Sirignano W A, Mehring C. Review of theory of distortion and disintegration of liquid streams[J]. Progress in Energy & Combustion Science, 2000, 26(4): 609–655. |
| [13] | Pritchard W. Instability and chaotic behaviour in a free-surface flow[J]. Journal of Fluid Mechanics, 1986, 165: 1–60. DOI:10.1017/S0022112086002987 |
| [14] | Mackowiak J. Fluid dynamics of packed columns[M]. London, New York:Springer, 2010. |
| [15] | Fair J R, Seibert A F, Behrens M, et al. Structured packing performance experimental evaluation of two predictive models[J]. Industrial & Engineering Chemistry Research, 2000, 39(6): 1788–1796. |
| [16] | Pavlenko A, Pecherkin N, Chekhovich V, et al. Hydrodynamics in falling liquid films on surfaces with complex geometry[J]. Microgravity Science and Technology, 2009, 21(1): 207–213. |
| [17] | Yao Y, Pavlenko A, Volodin O. Effects of layers and holes on performance of wire mesh packing[J]. Journal of Engineering Thermophysics, 2015, 24(3): 222–236. DOI:10.1134/S1810232815030042 |
| [18] | Kolev N, Kralev B, Kolev D. Gas side controlled mass transfer in a new packing with stamped horizontal lamellae operating at extremely low liquid loads[J]. Chemical Engineering and Processing:Process Intensification, 2013, 63: 44–49. DOI:10.1016/j.cep.2012.07.004 |
| [19] | 戴干策, 胡剑光, 于建国, 等. 适应粘性吸收剂的有壁与无壁液膜交替的规整填料: 中国, 201210234334. 6. 2013-07-10. Dai G C, Hu J G, Yu J G, et al. Wall liquid film and wall-free liquid film alternate structured filler adapting to viscous absorbent:China, 201210234334.6. 2013-07-10. |
| [20] | Hu J, Liu J, Yu J, et al. CO2 absorption into highly concentrated dea solution flowing over a vertical plate with rectangular windows[J]. International Journal of Greenhouse Gas Control, 2013, 19: 13–18. DOI:10.1016/j.ijggc.2013.08.007 |
| [21] | 胡剑光, 刘佳特, 袁猛, 等. 新型垂直板规整填料流体力学及传质性能[J]. 化工学报, 2014, 65(1): 116–122. Hu J G, Liu J T, Yuan M, et al. Hydrodynamics and mass transfer characteristics of a novel vertical-sheet structured packing[J]. Journal of Chemical Industry and Engineering, 2014, 65(1): 116–122. |
| [22] | 王良生, 戴干策. 圆盘反应器成膜性的持液量研究[J]. 化学反应工程与工艺, 2000, 16(2): 127–135. Wang L S, Dai G C. A study of film forming and hold-up in a rotating disc-ring reactor[J]. Chemical Reaction Engineering and Technology, 2000, 16(2): 127–135. |
| [23] | 邓斌, 戴干策. 圆盘反应器液膜表面更新数值模拟[J]. 化工学报, 2015, 66(4): 1407–1416. Deng B, Dai G C. Numerical simulation of surface renewal frequency on vertically rotating disc[J]. Journal of Chemical Industry and Engineering, 2015, 66(4): 1407–1416. DOI:10.11949/j.issn.0438-1157.20141688 |
| [24] | Hu J, Yang X, Dai G. Numerical investigation on hydrodynamics of vertically confined free film[J]. The Canadian Journal of Chemical Engineering, 2016, 94(2): 340–348. DOI:10.1002/cjce.v94.2 |
| [25] | Oliver J F, Huh C, Mason S G. Resistance to spreading of liquids by sharp edges[J]. Journal of Colloid and Interface Science, 1977, 59(3): 568–581. DOI:10.1016/0021-9797(77)90052-2 |
| [26] | Brunet P, Flesselles J-M, Limat L. Dynamics of a circular array of liquid columns[J]. The European Physical Journal B, 2007, 55(3): 297–322. DOI:10.1140/epjb/e2007-00057-y |
| [27] | Schmuki P, Laso M. On the stability of rivulet flow[J]. Journal of Fluid Mechanics, 1990, 215: 125–143. DOI:10.1017/S0022112090002580 |
| [28] | Ruan B, Jacobi A M, Li L. Effects of a countercurrent gas flow on falling-film mode transitions between horizontal tubes[J]. Experimental Thermal and Fluid Science, 2009, 33(8): 1216–1225. DOI:10.1016/j.expthermflusci.2009.07.009 |



