Φ0.5m高超声速风洞是目前国内高超领域的主力生产型风洞, 流场品质优秀, 承担了国内大量的航天飞行器风洞测力试验任务。对该风洞的试验进行不确定度分析, 其意义主要体现在2个方面:一是可以作为评价指标对试验数据进行质量评估。这历来都是飞行器设计部门十分关心的重要课题, 这是由于在飞行器研制过程中, 为了确保飞行器的稳定性、机动性, 对气动特性的变化范围有严格的要求, 控制系统设计也要求风洞所提供的气动特性不确定度范围不能太大, 否则难以控制; 二是可以有效指导风洞试验技术的提高。由于风洞试验是一个多环节的复杂过程, 每一环节所产生的数据测量都会受到各种误差源的影响, 并影响到最终试验结果。如何有效分辨各种误差源对最终试验结果的影响权重, 以对影响较大的误差源进行改进, 是该风洞最为关心的问题。
国外各研究中心自风洞承建以来就已展开气动力数据的不确定度分析工作。为了能够提供一套有效、通用的不确定度评定方法,并且能够适用于风洞复杂的试验条件与测试系统,1991年,AGARD专门成立了工作组,针对风洞试验的不确定度分析展开集中研究,1992年,AIAA的测试技术组(GTTC)也参与了进来。经过大量的研究工作,AGARD与AIAA对风洞试验的不确定度评定达成了共识,统一了评定方法。1994年,AGRAD出版了标准《Quality Assessment for Wind Tunnel》(AGARD-AR-304)[1];1995年,AIAA出版了标准《Assessment of Wind Tunnel Data Uncertainty》(AIAA S-071A-1995)[2]。2个标准(下文简称标准)在评定方法上是一致的,如图 1所示,主要特点是将随机误差和系统误差引入的不确定度分开计算,将随机误差引入的不确定度定义为精度极限PJ,将系统误差引入的不确定度定义为偏差极限BJ,再分别计算试验结果的精度极限Pr和偏差极限Br,最终合成得到标准不确定度。
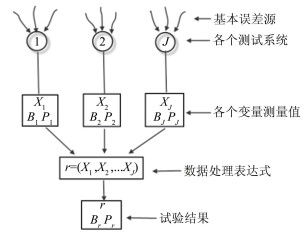
|
| 图 1 不确定度评估方案 Fig.1 Uncertainty assessment methodology |
标准采用的精度极限和偏差极限的分类方式,可以直接看出随机误差与系统误差的作用方式及比重结果,对于处理误差源众多,结构关系复杂的系统,效果良好。目前在可见的文献记载中,除了巴西的TA-2风洞未采用该标准[3],其他研究机构的风洞不确定度分析工作均依照该标准展开[4-12]。但该标准仅仅是提供了一种方法,内容并不全面,比如隐性自变量引入的不确定度计算方法、各不确定度源敏感性的计算方法等均未涉及。所以,在实际各种类型的风洞测力试验中,如何将该标准合理地应用并进行扩展,是研究者面临的主要问题。本文在该标准的基础上,结合Φ0.5m高超声速风洞的测力试验方法,对该标准进行了扩展,力求在现有技术水平的基础上,合理、全面地实现气动数据的不确定度分析。
1 评估流程 1.1 不确定度源辨识风洞的不确定度源辨识,需要以风洞的整个试验流程作为研究对象,梳理数据从传感器经过所有转换,直至最终结果的整个数据流动过程。风洞的测力试验方法决定了风洞的数据流动过程,数据流动的各个环节都会受到各种误差源的影响。不确定度源的辨识,需要以数据流动为基础,研究每一个步骤可能引入不确定度的误差源。
对于Φ0.5m高超声速风洞,首先根据体轴系天平公式计算得到相对天平校准中心的气动载荷,并对载荷进行天平安装滚转角的修正,将修正后的气动载荷与总压、模型参考长度等参数进一步处理,即可得到模型体轴系的气动力系数,力矩系数需要根据各项参考距离转换至模型的质心。在这个数据流动过程中,可从试验技术相关类、测试仪器相关类、试验模型相关类和风洞流场相关类展开不确定度源的辨识。受现有技术水平的限制,对于Φ0.5m高超声速风洞,试验模型相关的不确定度源及风洞流场的部分不确定度源,还未能实现定量评估,本文暂时未计及。表 1所示为本文的不确定评估计量在内的不确定度源。
| 类别 | 项目 | 具体源头 |
| 试验技术 | 天平校准 | 校准各环节误差 |
| 弹性角校准 | 校准各环节误差 | |
| 支撑机构 | 迎角运行误差 | |
| 侧滑角运行误差 | ||
| 天平滚转角 | 安装的误差 | |
| 参考长度测量 | 高度尺、游标卡尺等示值误差 | |
| 测量人员的读数误差 | ||
| 温度漂移 | 温度效应 | |
| 测试仪器 | 压力传感器 | 量程误差 |
| 分辨率 | ||
| K型热电偶 | 测量误差 | |
| 压力信号采集卡 | 量程误差 | |
| 截断误差 | ||
| 天平信号采集卡 | 量程误差 | |
| 线性偏差 | ||
| 风洞流场 | 马赫数校测 | 校测各环节误差 |
风洞数据处理时的各原始输入参数即为试验的自变量(X1、X2…Xr)。依次辨识得到所有的风洞不确定度源头后,需要对自变量进行具体的不确定度评估,包括其精度极限和偏差极限的具体值。
表 2所示为Φ0.5m高超声速风洞的自变量,对于表中的各项自变量,有的不确定度源只是表 1中的某一项,有的包含表 1所列的多项。可以按照测量不确定度的A类或B类评定方法,逐一进行分析评估。
| 参数 | 代号 | 单位 |
| 驻室压力 | pc1 | Pa |
| pc2 | Pa | |
| 模型底压 | pd1 | Pa |
| pd2 | Pa | |
| 总压 | △p01 | Pa |
| △p02 | Pa | |
| 运行迎角 | α0 | ° |
| 天平安装滚转角 | △φ | ° |
| 对质心力矩系数的参考距离 | lgz | m |
| lgx1 | m | |
| lgx2 | m | |
| 马赫数 | Ma | |
| 弹性角系数 | KαMz | °/kg/m |
| KαY | °/kg | |
| 天平各元载荷 | Q | kg |
| Y | kg | |
| Z | kg | |
| Mx | kg·m | |
| My | kg·m | |
| Mz | kg·m |
因变量的不确定度评估,是不确定度分析的最终目的。风洞数据处理时的结果输出参数是试验的因变量(r),对于Φ0.5m高超声速风洞,即为各迎角水平下的各气动力系数。在具体评估时,将表 2所述的自变量分成2部分展开:一为各压力值、参考距离等显性自变量;二为与迎角相关的隐性自变量。
1.3.1 显性自变量引入的不确定度评估对于显性自变量引入的不确定度,会通过数据处理表达式直接影响试验结果,可基本按照标准所述的方法展开评估。根据Φ0.5m高超声速风洞的数据流动过程,各气动力系数可写成如下各自变量的函数关系:
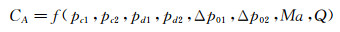 (1)
(1)
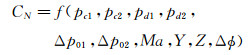 (2)
(2)
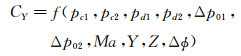 (3)
(3)
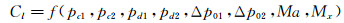 (4)
(4)
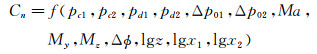 (5)
(5)
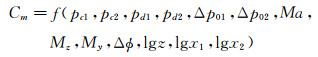 (6)
(6)
以轴向力系数CA为例,将显性自变量引入的偏差极限和精度极限记为BCA1和PCA1, 其具体值为:
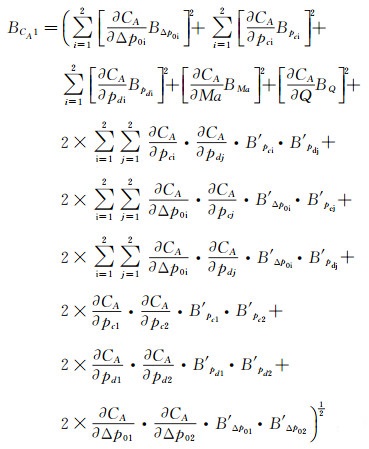 (7)
(7)
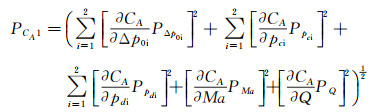 (8)
(8)
式(7) 中,B′为各压力之间的相关偏差极限。
1.3.2 迎角引入的不确定度评估标准仅考虑了显性自变量通过数据处理传播引入的不确定度,但在实际的风洞试验中,还存在隐性自变量。对于Φ0.5m高超声速风洞,流场的气流偏角与时变、试验模型的外型轮廓偏离理论外形、实际迎角与名义迎角的偏差等,都作为隐性自变量引入了不确定度,这些不确定度源不会通过数据处理影响试验数据,但会直接地影响试验结果。对于一个完整的不确定度评估流程,这些隐性自变量是应该予以考虑的,但精细地评估其引入的不确定度,难度巨大,目前不存在通用的方法。
本文仅对迎角引入的不确定度进行了估算。实际迎角α是迎角机构的运行迎角和弹性角修正的结果,数学模型为:
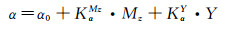 (9)
(9)
为保持与标准的一致性,把迎角的不确定度uα分为偏差极限Bα和精度极限Pα部分,具体值为:
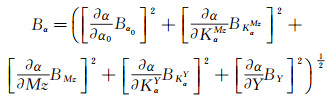 (10)
(10)
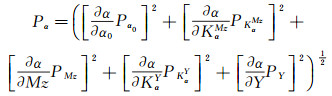 (11)
(11)
在小迎角范围内,可将各气动力系数近似看成随迎角线性变化,按照线性插值估算迎角引入的不确定度。仍以轴向力系数CA为例,以数据点(α1,CA(α1))作为评估对象,实际迎角α1存在不确定度uα,对于uα引入的不确定度uCA,可利用相邻数据点(α2,CA(α2)),由下式估算得到:
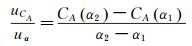 (12)
(12)
将uCA分为偏差极限BCA2和精度极限PCA2部分,具体值为:
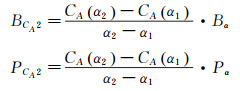 (13)
(13)
分别将显性自变量与迎角引入的偏差极限、精度极限进行方根和处理,即可得到最终结果的偏差极限和精度极限,再次方根和后可作为最终的不确定度结果,对于轴向力系数CA,可得到:
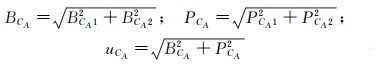 (14)
(14)
基于Matlab符号计算箱的计算功能实现上述流程的不确定度评估。图 2所示为在Matlab引擎中的不确定度计算流程,并以该程序作为不确定度分析的结果形式。首先定义各自变量及其偏差极限和精度极限,并根据数据处理表达式输入各因变量的符号表达式;然后可基于符号表达式对各自变量求偏导,得到各因变量偏差极限和精度极限的表达式;最后将各符号参数的参数值及偏差极限和精度极限代入,即可得到各因变量的不确定度结果。
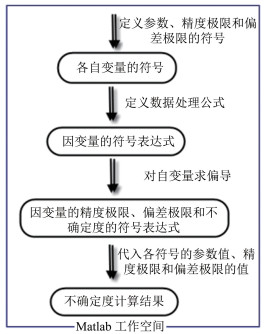
|
| 图 2 不确定度计算流程 Fig.2 Uncertainty assessment in Matlab |
对一升力体外形飞行器在Ma5基准状态的气动力试验数据进行评估,按照上述流程,以法向力系数CN、轴向力系数CA、俯仰力矩系数Cm 3项较为关注的结果为例,得到不确定度结果如表 3所示。
| α | CN | CA | Cm | ||||||||
| 偏差极限 | 精度极限 | 不确定度 | 偏差极限 | 精度极限 | 不确定度 | 偏差极限 | 精度极限 | 不确定度 | |||
| -10 | 0.02608 | 0.00273 | 0.02622 | 0.00404 | 0.00066 | 0.00409 | 0.00591 | 0.00203 | 0.00625 | ||
| -7.5 | 0.02135 | 0.00263 | 0.02151 | 0.00369 | 0.00065 | 0.00375 | 0.00487 | 0.00168 | 0.00515 | ||
| -5 | 0.01655 | 0.00257 | 0.01675 | 0.00336 | 0.00065 | 0.00342 | 0.00394 | 0.00133 | 0.00415 | ||
| -2.5 | 0.01167 | 0.00240 | 0.01192 | 0.00304 | 0.00064 | 0.00310 | 0.00276 | 0.00096 | 0.00293 | ||
| 0 | 0.00828 | 0.00240 | 0.00863 | 0.00281 | 0.00064 | 0.00289 | 0.00194 | 0.00072 | 0.00207 | ||
| 2.5 | 0.00753 | 0.00241 | 0.00790 | 0.00261 | 0.00063 | 0.00269 | 0.00145 | 0.00067 | 0.00160 | ||
| 5 | 0.01056 | 0.00251 | 0.01086 | 0.00250 | 0.00063 | 0.00258 | 0.00173 | 0.00087 | 0.00194 | ||
| 7.5 | 0.01554 | 0.00264 | 0.01576 | 0.00247 | 0.00063 | 0.00254 | 0.00258 | 0.00123 | 0.00286 | ||
| 10 | 0.02144 | 0.00291 | 0.02164 | 0.00245 | 0.00063 | 0.00253 | 0.00368 | 0.00166 | 0.00404 | ||
| 12.5 | 0.02820 | 0.00331 | 0.02839 | 0.00246 | 0.00063 | 0.00254 | 0.00495 | 0.00217 | 0.00541 | ||
| 15 | 0.03579 | 0.00372 | 0.03598 | 0.00245 | 0.00063 | 0.00253 | 0.00639 | 0.00274 | 0.00696 | ||
| 17.5 | 0.04393 | 0.00424 | 0.04414 | 0.00241 | 0.00063 | 0.00249 | 0.00794 | 0.00337 | 0.00862 | ||
| 20 | 0.05260 | 0.00470 | 0.05281 | 0.00236 | 0.00063 | 0.00244 | 0.00959 | 0.00339 | 0.01017 | ||
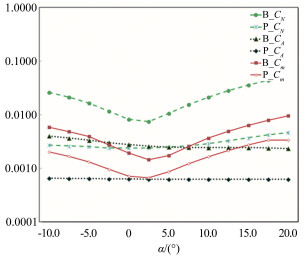
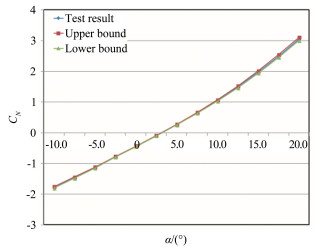
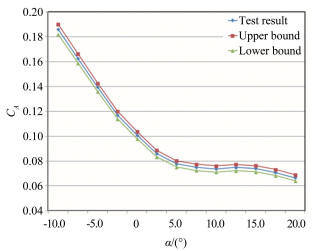
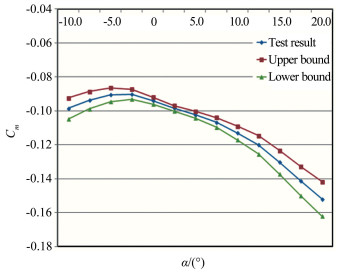
图 3所示为CN、CA和Cm的偏差极限和精度极限随迎角的变化规律。除此之外,根据表 3中的不确定度值,图 4至图 6所示为试验结果的分布范围。
|
| 图 3 试验结果的偏差极限和精度极限 Fig.3 Bias limit and precision limit of the test |
|
| 图 4 CN试验结果的分布范围 Fig.4 Distribution of CN |
|
| 图 5 CA试验结果的分布范围 Fig.5 Distribution of CA |
|
| 图 6 Cm试验结果的分布范围 Fig.6 Distribution of Cm |
由图 3可以看出,对于CN、CA和Cm,试验结果的偏差极限均要远远大于精度极限,这表明对于Φ0.5m高超声速风洞,系统误差引入的不确定度占主导地位,相比之下随机误差引入的不确定很小。
由图 4~6可见,CN、CA和Cm的不确定度随迎角的变化会出现一定的规律。究其原因,发现并非是各自变量的精度极限和偏差极限随迎角变化,主要是因变量的参数值在不断变化,经过不确定度的传播,使因变量的不确定度值出现随迎角变化的规律。所以,该变化规律对于不同的模型来讲,是不一样的。
对于该模型,CN的不确定度相比于自身较小,试验结果的不确定度带较窄,主要原因是法向力系数的参数值较大。并且在2.5°迎角附近,由于CN的参数值趋近于0,其不确定度的变化规律在该处出现拐点。Cm的不确定度相比于自身较大,主要是由于在Cm的计算过程中,需要首先计算得到相对于天平校准中心的力矩系数,并根据试验前测量得到的参考距离进行坐标系转换,在转换过程中,法向力系数和参考距离都会再次引入额外的不确定度。
2.2 不确定度的敏感性分析计算得到不确定度结果后,对各自变量的敏感性进行了估算,以得到自变量对最终不确定度结果的影响程度。以轴向力系数CA为例:
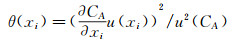 (15)
(15)
将式(15) 作为自变量xi在不确定度结果中的敏感性因子,忽略各个被测变量之间的相关性。
对于该模型,通过对CN各自变量的不确定度敏感性计算,发现对CN的不确定度结果起主导作用的自变量是总压传感器、天平和迎角。图 7所示为3者在迎角变化中敏感性的变化规律。可见在法向力的参数值很小时(2.5°迎角附近),天平和迎角机构是最大的不确定度源,随着法向力参数值的增大,总压传感器引入的不确定度开始占主导作用。
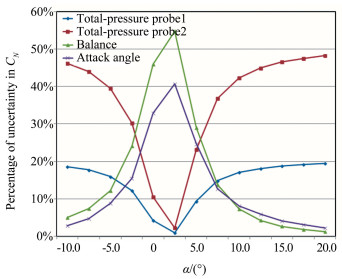
|
| 图 7 CN主要自变量的敏感性随迎角的变化 Fig.7 Senstitivity of independent variables at different attack angles |
通过对CA各自变量的不确定度敏感性计算,发现对CA的不确定度结果起主导作用的自变量只有总压传感器和天平。图 8所示为2个总压传感器和天平在迎角变化中敏感性的变化规律。可见随着迎角的增大,由于CA的参数值在逐渐减小,天平引入的不确定度在逐渐增加,这个过程使总压传感器引入的不确定度在相对变小。
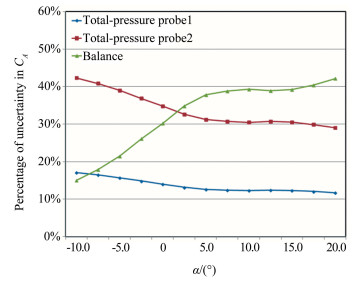
|
| 图 8 CA主要自变量的敏感性随迎角的变化 Fig.8 Sensitivity of independent variables at different attack angles |
在Cm不确定度敏感性的计算过程中,由于CN的结果会给Cm引入不确定度,但CN作为一个因变量,其很多自变量和Cm是一样的,此时若按标准方法计算各个自变量的敏感性,计算工作量过于巨大,并且对于探讨作用规律来讲,也并不直观。此时,将CN作为一个自变量进行敏感性的计算,发现CN在Cm中引入的不确定度相比于其它自变量占主导作用,这也导致Cm不确定度的整体变化规律和CN是一致的。
3 方法讨论不确定度的计算,历来相关性的处理是一个难题,主要是由于其关系繁琐,计算量巨大。在实际工程中,大多数自变量之间都是弱相关,对最终结果的影响不大。本文在的不确定度计算中,仅定量计算了各个压力传感器因采用相同的信号采集卡所引入的相关性,其它诸如天平各个载荷单元之间的相关性、同一操作人员采用同一测量设备测量各参考距离之间的相关性等,则暂时未予以考虑。尤其是在Cm的不确定度评估中,由于把CN当做自变量,这导致CN与其它自变量之间存在相关性,但这种相关性的定量评估,计算量是相当大的,缺少相关性的计算,得到的Cm的不确定度值是偏小的。
关于隐性自变量引入的不确定度,本文仅考虑了迎角,关于流场、模型等其它隐性自变量,目前还未能实现定量评估。首要原因是难以考察各项隐性自变量的单独作用效果,例如为定量考察模型加工引入的不确定度,可加工几套试验模型开展吹风试验,考察其试验结果的差异,但试验过程中风洞流场也会一并引入误差,得到的试验数据是各因素同时作用的结果。目前可行的方法只能是结合CFD和试验经验对其进行一定程度的估算,该工作将在后续不断深入。
对于Φ0.5m高超声速风洞,本文选用的评估实例具有代表性,表明天平和总压传感器是试验结果最大的不确定度源,因此改善天平技术和总压测量应是目前该风洞试验技术提高的方向。对于总压测量,最直接的方法是更换更高精准度的传感器。对于天平技术,一方面:天平的校准不确定度是一个综合考察结果,可据此对天平设计、天平校准等环节进行具体改善;另一方面:由于试验的载荷值越小,天平引入的不确定度越大,这要求在实际试验中选用天平时要匹配载荷,应避免采用大量程的天平测量小载荷的气动力。
4 结论本文在评估Φ0.5m高超声速风洞的过程中,受现有技术水平的限制,风洞中的部分不确定度源还无法做到定量评估,暂时未予以考虑,并且在评估的具体细节中,对部分计算进行了简化。所以当前结果对于评估气动数据的不确定度来讲,只是一种估算,后续随着计量水平的提高,方法将不断进行改善。但目前所得结果能够有效指明当前的主要不确定度源,这对于提高风洞试验技术这一目的来讲,是有效的。通过研究工作,可以得到如下结论:
(1) 系统误差引入的不确定度占主导地位,相比之下随机误差引入的不确定很小。
(2) CN的不确定度相比于自身较小,Cm的不确定度相比于自身较大,并且在试验中不同迎角时不确定度值会出现显著的差异。
(3) 总体来讲,天平和总压传感器引入的不确定度占主要部分,并且气动载荷越小,天平引入的不确定度相对越大。
| [1] | AGARD. Quality assessment for wind tunnel[R]. AGARD-AR-304, 1994. |
| [2] | Anon. Assessment of wind tunnel data uncertainty[R]. AIAA-S-071-1995, 1995. |
| [3] | Olympio A F M, Sadahaki Y. Uncertainty methodology at the brazilian TA-2 subsonic wind tunnel[R]. AIAA-98-2716, 1998. |
| [4] | Ulbrich N, Boone A R. Uncertaity analysis of test data in the ames 11-foot transonic wind tunnel[R]. AIAA-2004-2195, 2004. |
| [5] | Shinji N, Hidetoshi I. Uncertainty identification of supersonic wind-tunnel testing[J]. Journal of Aircraft, 2011, 48(2): 567–577. DOI:10.2514/1.C031159 |
| [6] | Michael J H, Jeremy L H. Detailed uncertainty analysis for ares I ascent aerodynamics wind tunnel database[R]. AIAA-2008-4259, 2008. |
| [7] | Eric R H, Mark E K. Aerodynamic and aerothermal instrumentation:measurement uncertainty in the NSWC hypervelocity wind tunnel[R]. AIAA-96-2210, 1996. |
| [8] | Dale L B. Application of uncertainty methodology at the boeing aerodynamics laboratory[R]. AIAA-96-2215, 1996. |
| [9] | Cahill D M. Application of uncertainty methodology for the wind tunnel facilities at AEDC[R]. AIAA-96-2216, 1996. |
| [10] | Anthony M S. Uncertainty analysis of the NASA MSFC 14-inch trisonic wind tunnel[R]. AIAA-99-0684, 1999. |
| [11] | 谢疆宇, 吴军强, 钟世东, 等. 2.4m跨声速风洞大型飞机试验不确定度评估[J]. 实验流体力学, 2010, 24(6): 65–68. Xie J Y, Wu J Q, Zhong S D, et al. Uncertainty analysis for large aircraft test in 2.4m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(6): 65–68. |
| [12] | 王刚, 唐志共, 吕治国, 等. 激波风洞气动力试验不确定度影响因素分析[J]. 实验流体力学, 2013, 27(2): 87–90. Wang G, Tang Z G, Lyu Z G, et al. Analysis of uncertainty for aerodynamic test in shock tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(2): 87–90. |



