高超声速风洞基本采用暂冲式运行方式, 其真空系统的组成主要为真空罐和真空机组, 作用是提供风洞运行所需的真空环境, 即保证风洞起动和稳定运行一段时间。暂冲式高超声速风洞的流场建立后, 其真空罐内的压力持续升高, 升高到某一值后才导致试验段稳定的环境压力发生脉动式上升的变化, 同时流场开始发生破坏, 真空罐对应该破坏点时的压力值称为临界压力或结束压力; 临界压力比为临界压力与对应状态皮托压力(也称为超声速/高超声速气流正激波后等熵滞止的压力)的比值。风洞运行中从起动压力到临界压力的时间为风洞有效运行时间。吹吸式风洞的真空系统较容易满足起动压力要求, 于是临界压力比和有效运行时间直接决定了真空系统的规模。有效运行时间是风洞的总体技术指标之一, 在真空系统设计前已经是确定值,所以影响真空系统设计的因素是临界压力比。
真空系统往往在高超声速风洞建设成本中占较大的比例。对于大型高马赫数的高超声速风洞,由于流场马赫数高,维持流动需要更高的压力比,于是真空系统建设成本所占比例更大。在大型高马赫数的高超声速风洞设计前需准确获得临界压力比才可既满足流场维持时间需求,又可有效预测建设成本。故临界压力比的较准确获得成为亟待研究解决的基础问题之一。
A. Pope和K. L. Goin 1965年给出了暂冲式风洞运行时间与真空容积、开始压力、结束压力、真空泵抽吸速率的关系[1], 但没有提供结束压力的确定。徐华舫1987年给出了喷管工作的4种工作状态及划界压力[2],可用于了解风洞喷管流场从建立到破坏的压力变化情况。高超声速风洞真空系统临界压力比经验上取0.1[3-6],该取值较为保守,且马赫数适用范围小于10,马赫数10以上的流场所需的真空系统临界压力比研究尚未见公开报道[7-13]。
喷管出来的高超声速气流进入真空系统前一般还经过模型、扩压器、冷却器、真空管道等,均会导致压力损失,影响临界压力比,但是扩压器[7]和冷却器中的流动复杂,且风洞起动到结束为非定常流动,真实的全流场数值模拟难度大,给临界压力比的确定带来困难。目前真空系统设计中一般参考经验,故而在真空系统设计方面往往偏于保守,不利于大型高超声速风洞的成本控制。本文从大型Ma10以上的风洞设备设计需求出发,通过在中国空气动力研究与发展中心Φ0.3m高超声速低密度风洞中进行了Ma10以上喷管流场破坏时临界压力的实验研究,了解扩压器内的流动变化和实验段流场破坏过程,确定了高马赫数流场的临界压力比,为类似大型风洞的真空系统设计提供了依据。
1 实验设备和测试仪器 1.1 风洞实验在CARDC的Φ0.3m高超声速低密度风洞(风洞代号FD-17) 上进行,该风洞是一座典型的高压下吹、真空抽吸的暂冲运行风洞。风洞由气源系统、加热器、稳定段、喷管、实验段、扩压段、冷却器、真空系统和测试系统等部分组成。该风洞目前配备有型面喷管8套,喷管出口马赫数为5、6、7、8、9、10、11和12;锥形喷管3套,喷管出口马赫数为12、16和24,所有喷管出口直径均为Φ300mm。介质为氮气或空气,实验根据不同的状态可分别选用石墨电阻加热器或储热式加热器进行加热或不加热。本次实验用喷管是出口马赫数为10和12的型面喷管以及16的锥形喷管,介质为氮气,测量参数包括总压、总温、风洞实验段静压、流场的皮托压力、扩压器内表面前后壁面压力和真空罐压力等,测试位置示意如图 1所示。
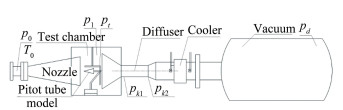
|
| 图 1 设备安装示意图 Fig.1 Sketch ofmeasurement points in low density wind tunnel |
(1) 总压采用CYG105型压阻传感器测量,量程分别0~4MPa和0~10MPa,根据总压范围选用。
(2) 皮托压力采用CYG219(量程0~10kPa)和CYG222(量程0~2500Pa)型压阻传感器测量。
(3) 实验段环境压力采用ZDZ-52电阻规真空和ZDO-53热偶真空计测量。实验段环境压力波动是判断流场开始破坏的依据,故在实验段侧壁2个位置分别用ZDZ-52电阻真空计和ZDO-53热偶真空计同时测量或监控其变化,并在使用前进行了标定,标定曲线如图 2和3所示。
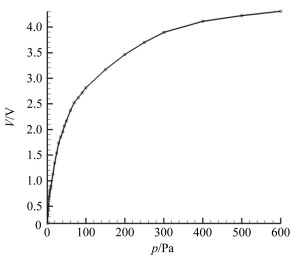
|
| 图 2 ZDZ-52电阻真空计输出电压和压力曲线 Fig.2 Calibration curve of ZDZ-52 vacuum gauge |
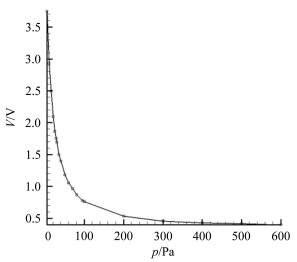
|
| 图 3 ZDO-53热偶真空计输出电压和压力曲线 Fig.3 Calibration curve of ZDO-53 vacuum gauge |
(4) 扩压器前后压力采用CYG222(0~2500Pa)型压阻传感器测量。
(5) 真空罐压力采用罗斯蒙特绝对压力变送器(0~6kPa)测量,并在使用前进行了标定,标定曲线如图 4所示。
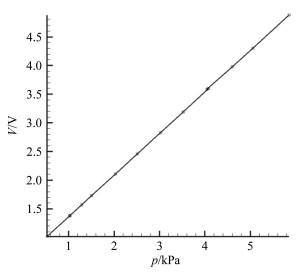
|
| 图 4 压力变送器输出电压和压力校准结果 Fig.4 Calibration result of Rosemount transducer |
(6) 数采系统采用32通道数采系统进行数据采集,采用频率100Hz。
2 实验方法、实验状态 2.1 实验方法通过测量实验过程中的实验段静压、流场皮托压力、真空球罐末端压力和扩压器前后壁面压力,并结合已知的风洞参数及实验状态参数,确定当实验段流场遭到破坏时的实验段皮托压力与真空罐压力之间的关系,从而得出不同马赫数的临界压力比;通过扩压器前后壁面压力变化,了解激波在扩压器内的位置变化情况。
2.2 实验状态本次实验状态共3个,分别为:(1) 状态1:喷管Ma16,p0=2.36×106Pa,T0=909K;(2) 状态2:喷管Ma12,p0=1.04×107Pa,T0=753K;(3) 状态3:喷管Ma10,p0=7.51×106Pa,T0=650K。
2.3 实验数据处理方法实验段流场遭到破坏时,对应实验段静压波动,对应此时真空球罐的压力pd就是实验需要获得的临界压力。为更好比较不同马赫数流场破坏时的临界压力,以实验段皮托压力p02为参考进行无量纲化,二者的比值η作为临界压力比,即:
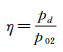 (1)
(1)
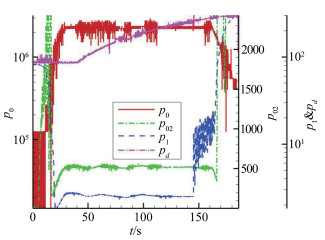
在Ma10~16实验过程中,稳定段总压和总温、实验段环境压力、扩压器前后静压、冷却器前后总压和静压、真空罐压力变化趋势基本一致。图 5是稳定段总压p0、皮托压力p02、实验段环境压力p1、真空罐压力pd随实验时间的数据曲线,可以看出,风洞起动后,真空计监测的实验段环境压力迅速稳定,但在实验结束前出现信号的波动,表明实验段流场稳定了一段时间而后被破坏;稳定段总压p0和皮托压力p02迅速稳定,表明实验过程中气体供应平稳;由于真空泵的抽吸作用和进气流量的相互作用,真空罐压力pd保持短暂稳定时间后持续升高,表明进入真空罐的气体来不及被抽走,累积的越来越多;实验段环境压力p1稳定一段时间后出现震荡上升,说明流场已经破坏,震荡开始点即为流场破坏的起始点,该起始点对应的真空罐压力pd即为临界压力。
|
| 图 5 稳定段总压、皮托压力、实验段环境压力、真空罐压力数据曲线(状态1) Fig.5 Pressure variation curves of stagnation (p0) and pitot (p02) and test section environment (p1) and vacuum container (pd) (Case 1) |
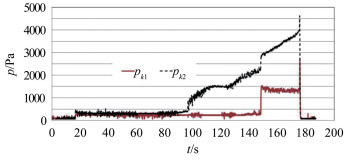
图 6为扩压器前后的壁面压力随实验时间的数据曲线,壁面压力稳定了一段时间后,扩压器后端的壁面压力先升高,再持续升高,经过一段时间后扩压器前端的壁面压力升高,表明扩压器内的流动先稳定一段时间后有激波从后端往前传来。
|
| 图 6 扩压器前后静压典型变化图(状态3) Fig.6 Pressure variation curves of diffuser ahead (pk1) and behind (pk2) during the experiment (Case 3) |
从整个实验过程中各处的压力变化可以看出,实验的流动过程可描述如下:风洞即将起动前,真空罐和实验段的压力较低,风洞起动后,稳定段稳定的气体通过喷管加速至高超声速流动,进入扩压器,并产生引射作用,导致实验段环境压力从实验前的值下降至流场静压的大小,扩压器内部和出口均为超声速流动,而后进入真空罐滞止。随着真空罐的压力逐渐升高到一定程度后,超声速气流进入真空罐前产生激波,并且该激波位置随着真空罐压力的进一步升高逐渐顺着扩压器、实验段方向往前移动,当激波移至扩压器入口时,实验段的流场也就被破坏了,实验结束。由此可分析出,在来流条件和风洞设备不变的情况下,真空罐的压力是决定风洞实验过程中激波在扩压器中的位置,临界压力pd决定实验段流场破坏及实验运行时间。
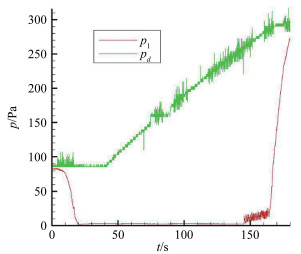
图 7是状态1(Ma16喷管、稳定段总压p0为2.36×106Pa、稳定段总温T0为909K、皮托压力p02为535Pa)实验段环境压力、真空罐压力数据曲线,可以确定临界压力pd为267Pa,由式(1) 得η=0.5。
|
| 图 7 实验段环境压力、真空罐压力数据曲线(状态1) Fig.7 Pressure variation curves of section environment (p1) and vacuum container (pd) (Case 1) |
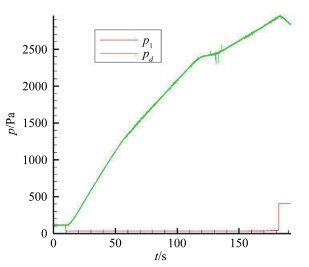
图 8是状态2(Ma12喷管、稳定段总压p0为1.04×107Pa、稳定段总温T0为753K、皮托压力p02为7578Pa)实验段环境压力、真空罐压力数据曲线,可以确定临界压力pd为2631Pa,由式(1) 得η=0.35。
|
| 图 8 实验段环境压力、真空罐压力数据曲线(状态2) Fig.8 Pressure variation curves of section environment (p1) and vacuum container (pd) (Case 2) |
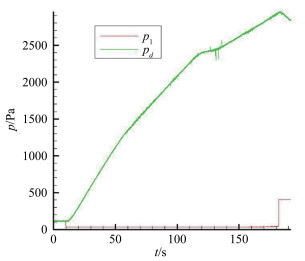
图 9是状态3(Ma10喷管、稳定段总压p0为7.51×106Pa、稳定段总温T0为650K、皮托压力p02为14 409Pa)实验段环境压力、真空罐压力数据曲线,可以确定临界压力pd为4913Pa,由式(1) 得η=0.34。
|
| 图 9 实验段环境压力、真空罐压力数据曲线(状态3) Fig.9 Pressure variation curves of section environment (p1) and vacuum container (pd) (Case 3) |
从图 8~10获得了Φ0.3m高超声速低密度风洞Ma10~16喷管流场所需的真空系统临界压力比,由于风洞扩压器、冷却器等影响,作为大型同类高超声速风洞的真空系统设计而言η取0.3是合适的,既能够满足所有的状态,又比按η取0.1的真空规模缩减2/3。
|
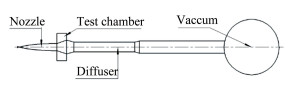
| 图 10 风洞计算用型面图 Fig.10 Wind tunnel sketch for numerical simulation |
近期,1m量级Ma10至16高超声速风洞的初步调试结果表明其临界压力比在0.304~0.312之间,与设计值较为符合。
4 流场模拟结果高超声速风洞冷却器的冷却管位于流场中,前后交错排布,真实外型面三维网格生成复杂,而风洞其余部段均可假设为轴对称,可采用二维网格,若考虑包含冷却管的全流场数值模拟,则需全部采用三维网格计算,给全流场的非定常流动数值模拟带来很大的计算量。为便于开展计算,对风洞计算的内型面进行了简化,在保证喷管型面与扩压器入口直径和等直段内径(Φ0.4m)及相对位置关系与实际一致的前提下,不考虑冷却管,对真空罐和真空管道尺寸进行了适当缩小,整个计算型面如图 10所示。数值模拟采用FASTRAN软件,对3个实验状态的全流场进行了模拟。
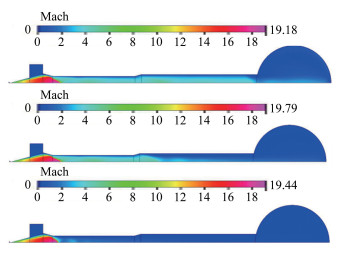
图 11从上往下给出了状态1实验段流场建立、稳定和即将破坏时的全流场马赫数云图,可以看到激波随真空罐压力升高从真空管道向扩压器入口运动的过程,其扩压器内的运动过程与图 6试验结果趋势一致。图 12是对应图 11中激波运动到扩压器入口时的球罐内压力云图,可看出流场即将破坏时,真空球罐内压力分布最大相差4Pa,平均值约为303Pa。
|
| 图 11 风洞全流场马赫数云图(状态1) Fig.11 Mach number contour of wind tunnel flow field(Case 1) |

|
| 图 12 真空球罐压力云图(状态1) Fig.12 Pressure contour of vacuum container(Case 1) |
同理给出了状态2和3的结果,表 1给出3个实验状态的临界压力测量结果和数值模拟的计算结果,可以看出临界压力的计算结果均比实验结果略高,主要是因为计算中未考虑冷却器,压力损失比实际实验中的低。
| 来流状态 | 临界压力实验结果 | 临界压力计算结果 |
| 状态1 | 267 | 303 |
| 状态2 | 2631 | 2700 |
| 状态3 | 4913 | 5600 |
(1) 在来流条件和风洞设备不变的情况下,真空罐的压力是决定风洞实验过程中激波在扩压器中的位置,临界压力pd决定实验段流场破坏及实验运行时间。
(2) Φ0.3m高超声速低密度风洞Ma10~16喷管流场所需的真空系统临界压力比,可类推作为大型同类型高超声速风洞真空系统设计的重要参数,既能够满足所有的状态,又能够控制真空建设规模。从1m量级Ma10~16高超声速风洞的初步调试结果也验证了临界压力比取值的合理性。
(3) Φ0.3m高超声速低密度风洞简化外形的全流场数值模拟结果提供了流场从建立至破坏的过程,临界压力计算结果比实验结果略高,原因是计算中未考虑冷却器。
| [1] | 博普A., 戈因K.L.. 高速风洞试验[M]. 北京: 科学出版社, 1980. |
| [2] | 徐华舫. 空气动力学基础[M]. 北京: 北京航空学院出版社, 1987. |
| [3] | 伍荣林, 王振羽. 风洞设计原理[M]. 北京: 北京航空学院出版社, 1985. |
| [4] | Smelt R, Sivells J C. Design and operation of hypersonic wind tunnels[J]. JAS, 1953. |
| [5] | 徐翔, 伍贻兆, 程克明, 等. 高超声速风洞气动布局设计[J]. 南京航空航天大学学报, 2008, 40(2): 271–274. Xu X, Wu Y Z, Cheng K M, et al. Aerodynamic configuration design of hypersonic wind tunnwls[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(2): 271–274. |
| [6] | 侯峰伟, 吴斌, 齐大伟. 高超声速风洞真空保障系统改造[J]. 真空, 2014, 52(5): 36–38. Hou F W, Wu B, Qi D W. Reformation of vacuum system in hypersonic wind tunnel[J]. Vacuum, 2014, 52(5): 36–38. |
| [7] | 童华, 孙启志, 张绍武. 高超声速风洞扩压器试验研究与分析[J]. 实验流体力学, 2014, 28(3): 78–81. Tong H, Sun Q Z, Zhang S W. Investigation and analyse on the diffuser of hypersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(3): 78–81. DOI:10.11729/syltlx20120201 |
| [8] | Nomura S, Sakakibara S, Hozumi K, et al. NAL new hypersonic wind tunnel system[R]. AIAA-93-5006, 1993. |
| [9] | Koppenwallner G. Low density facilities[M]. Gottingen: , 1995. |
| [10] | 佛兰克K, 陆丹, 马伦E. 先进高超声速试验设备[M]. 北京: 航空工业出版社, 2015. |
| [11] | Anfimov N. Tsniimash capabilities for acrogasdynamical and thermal testing of hypersonic vehicles[R]. AIAA-92-3962, 1992. |
| [12] | Bishop R M. New AEDC wind tunnel capabilities[R]. AIAA-2000-0162, 2000. |
| [13] | Coblish J J, Spring S, Davenport A H. Recent efforts at AEDC's Von karman facility and hypervelocity wind tunnel 9 to enhace facility compatibility[R]. AIAA-2002-2782, 2002. |



