2. 中国科学院力学研究所 非线性力学国家重点实验室, 北京 100190
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
水和气体、固体间的界面问题无处不在,且在生活及大多数工业领域都十分重要[1]。近年来随着流动尺度的进一步减小,纳流控应运而生,在生物芯片技术、新能源领域及微纳尺度化学分析等方面都有广阔的应用前景[2]。溶液中,固体表面会从溶液中选择性地吸附离子或是固体表面的带电基团解离而带电。根据电中性原理,带电表面附近的液体中必有与固体表面电荷数量相等但符号相反的反离子,带电表面和反离子构成双电层。由于电荷分离而造成的液固两相内部的电位差称为表面电势。表面电荷/表面电势引起的双电层会对微纳米尺度的流体流动产生重要影响[1, 3]。因此精确测量双电层内表面电势/表面电荷密度,进而有效调控表面电势/表面电荷密度显得尤为重要。
传统测量液固界面表面电势及表面电荷密度的方法有流动电位法及电渗法[4-5]。Kirby[4]等人通过流动电位法间接测量了硅基表面的zeta电势。在外力驱动下,微通道中液体流动带动带电离子沿流动方向运动,使电荷在下游沉积,产生电位差,即流动电位,从而通过计算得到zeta电势。电渗法则是通过测量电渗流速度间接测量zeta电势。这2种方法都是测量双电层中的扩散层自由电荷相对液固界面的输运,其界面电势是基于剪切滑移面定义的,即zeta电势。DLVO理论[1]描述了液固界面带电表面相互作用力,包括范德华力和静电力。而由静电排斥定义的表面电势直接基于液固界面,不受滑移面位置的影响,是更能代表液固界面的本征属性[1, 6-7]。基于DLVO理论,本文改进了AFM胶体探针测量表面电势ψ的方法。考虑到近年来硅基材料在MEMS传感器上的广泛应用[8],测量硅基材料液固界面作用力、表面电势以及表面电荷密度对MEMS传感器的研究有着重要的实践意义,同时也是实验流体测量技术在微纳尺度的重要发展。
1 实验部分 1.1 实验测量方法本实验基于原子力显微镜胶体探针技术测量表面电势,仪器采用Asylum Research公司的MFP-3DTM原子力显微镜。图 1为AFM液下工作原理示意图。胶体探针由胶体球和无针尖悬臂梁粘结,在实验室自行加工而成(详见下文1.2节)。胶体探针由压电控制器控制以恒定速度接近样品表面,过程中受到静电力、水动力学阻力及范德华力作用,这些力的综合作用使得悬臂梁(Cantilever)产生微小变形。所以当激光(Laser)照射到悬臂梁末端时,其反射光的位置也会发生变化,造成偏移量的产生,悬臂梁的变形可由偏移量在光电位置敏感器件(Position sensitive detector)上的反馈得到。基于胡克定律,通过变形量及悬臂梁弹性系数可测得力。图 1中,Zs为系统基准位置位移,向上为正方向,由AFM中压电传感器测量得出;drect为胶体探针弹性变形,大小可由前述激光反射位移偏移量决定;D由Zs和drect计算得到。基于此测试系统,由Igor Pro软件可直接得胶体探针表面到基底之间距离D与胶体探针所受DLVO力和水动力学阻力关系曲线。在无滑移边界条件下的牛顿流体中,球面接近平面过程中所受水动力学阻力可由公式(1) 描述[9]:
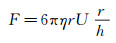 (1)
(1)
|
| 图 1 AFM液下工作原理示意图 Fig.1 AFM work principle sketch maps in fluid |
式中:η为水动力学粘滞系数;r为球半径;U为接近速度;h为球面与平面距离。所以,液体环境下,当胶体探针(直径为20.0±0.5μm)以极低的速度(10nm/s量级)接近样品底面时,在距离壁面10nm左右位置,水动力学阻力最大只有约10-11N,而本实验关注的DLVO力量级在10-9N量级,相比之下水动力学阻力可忽略不计,本实验只考虑静电力与范德华力。
1.2 AFM胶体探针制作及其弹性系数测量实验采用直径为20.0±0.5μm的二氧化硅小球(Duke Scientific,此种微球表面粗糙度最小[10])。取适量小球颗粒放到烧杯中,加入无水乙醇,超声清洗5min,重复此步骤2次。清洗完成后用普通标准探针(Asylum Research)扫描小球工作区域形貌,表面RMS均方根粗糙度在1nm以下(扫描范围5μm×5μm),如图 2所示。

|
| 图 2 AFM扫描小球形貌图 Fig.2 Sphere surface topography obtained from AFM |
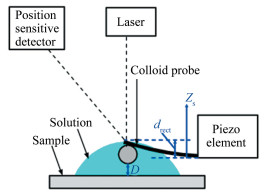
超纯水超声清洗盖玻片30h,烘干备用。AFM胶体探针具体制作步骤如图 3所示:使用移液器量取100μL清洗后小球与乙醇混合液滴在干净的盖玻片上,烘干晾至室温,如图 3(1)和(2)所示;然后将混合均匀的环氧树脂AB胶粘取针尖大小到盖玻片上。将此盖玻片放到实验平台上,利用AFM测试系统使无针尖悬臂梁(Nano Sensors,弹性系数0.12N/m,厚2.0±1μm,长450±10μm, 宽50±7.5μm)接近胶水表面,黏着少量胶水,如图 3(3)和(4)所示;然后上移无针尖悬臂梁,左右移动测试系统水平XY调节平台,找到合适的二氧化硅小球。慢慢使无针尖悬臂梁下降,同时左右移动测试系统XY调节平台,使小球正对悬臂梁下方,悬臂梁下降至接触到小球为止,等待1min左右,上移悬臂梁,等待胶水完全凝结,此时胶体探针制作完成,如图 3(5)和(6)所示。
|
| 图 3 胶体探针制作步骤 Fig.3 The fabrication procedure of colloidal probe |
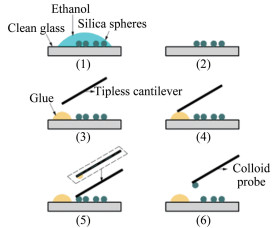
探针弹性系数的测量方法有几何法[11]、热噪声法[12]、水动力学法[13-14]和附加质量法[15]等,本实验采用系统自带热噪声法标定普通探针弹性系数。实验所用普通探针为Bruker公司的探针,热噪声法测得弹性系数为krect=0.15N/m (误差在4%内)。因胶体探针上小球质量比悬臂梁大得多,故不能使用热噪声法测胶体探针弹性系数。本实验欲采用双探针法测胶体探针弹性系数,即用普通探针压迫胶体探针使其形变,测量原理如图 4所示。将胶体探针固定到盖玻片上,普通探针安装在AFM上,普通探针下压胶体探针过程中,2探针产生形变,设变形量分别为drect、dprobe,弹性系数分别为krect、kprobe,弹性力为F。2个探针的受力变形过程可看作是2弹性体的串联,则总弹性系数为k=krect×kprobe/(krect+kprobe),总变形量为d= drect+dprobe。由AFM测试系统可得F与d关系曲线,斜率的绝对值即为k,此时可得到kprobe= krect×k/(k-krect)。实验测得自行粘结胶体探针弹性系数为0.27±0.05N/m。本实验用此双探针法实际测量了胶体探针的弹性系数,比仅仅通过几何法或热噪声法得到的简单估算值更加可靠。由于2探针受力过程可相当于一个两弹簧串联模型,一般认为2探针变形量越接近则测得的弹性系数越接近真值,且不易因探针悬臂梁弯曲过大而受损坏。本实验结果也表明当用来标定的标准探针弹性系数接近胶体探针弹性系数时测量结果的重复性较好。
|
| 图 4 双探针法测胶体探针弹性系数示意图 Fig.4 Schematic of measuring colloidal probe spring constant based on cantilever to cantilever device |
AFM胶体探针是通过测量胶体探针受到带电表面的作用力来测量表面电势及表面电荷密度的。基于DLVO理论,胶体探针与表面之间的相互作用力为范德华力和静电力之和,其相互作用能表达式为:
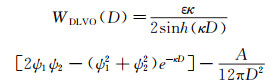 (2)
(2)
(2) 式右侧第一项表示静电力的作用能,第二项表示范德华力作用能。基于Derjaguin近似,相互作用力为[1, 6-7]:
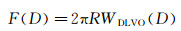 (3)
(3)
由公式(2)、(3) 得:
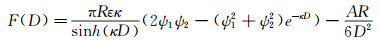 (4)
(4)
(4) 式中,ε为介电常数,к-1为德拜(Debye)长度,ψ1为探针表面电势,ψ2为基底表面电势,D为探针与壁面接触面距壁面距离,R为探针球半径,A为Hamaker常数,取1.2×1020J。此处含有3个未知数;к-1、ψ1和ψ2,由公式(4) 可知,表面电势ψ1和ψ2由静电力部分决定。一般认为,静电力主导的作用范围在距离壁面2к-1~3к-1的范围内,因此,对此范围的力曲线进行线性拟合即可得德拜(Debye)长度к-1的倒数к。理论上,如果确定了ψ1,就可以通过力曲线拟合唯一确定待测表面电势ψ2。因此,表面电势ψ2的确定需要2步:(1) 对称结构测探针表面电势ψ1。选用和探针材质相同的SiO2作基底,即SiO2-SiO2,此时,ψ1=ψ2。通过AFM测试系统可得DLVO力与距离D关系,将此实验数据与公式(4) 中理论曲线在2к-1~3к-1范围内拟合得探针表面电势ψ1;(2) 非对称结构测基底表面电势,例如选用氮化硅表面做基底,即SiO2-Si3N4。将第(1) 步中得到的探针表面电势ψ1代入公式(4),此时只剩一个未知数ψ2。采用同样的方法,将在氮化硅表面所测实验数据与理论力曲线拟合可得氮化硅表面电势ψ2。
此法也为测量表面电荷密度提供新思路。扩散层中,由Grahame方程可得表面电荷密度与表面电势关系,
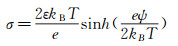 (5)
(5)
式中:ε为介电常数;kB为玻尔兹曼常数;T为温度;e为电子数。基于电中性原理,液固界面的表面电荷密度应与扩散层中的反电荷中和。因此,一定液体环境下,已知表面电势就可以唯一确定表面电荷密度。
1.4 基底制备等离子体辅助化学气相沉积(Plasma Enhanced Chemical Vapor Deposition,PECVD)属于化学气相沉积的一种类型,主要是借助施加一个射频功率产生辉光放电等离子体,使反应气体发生化学反应形成介质薄膜的技术。
本实验采用此技术制备氮化硅和二氧化硅薄膜,步骤如下:(1) 取直径大小为2inch,厚500μm<100>的单面抛光硅片若干片,放入体积比为浓H2SO4: H2O2= 7: 3的混合溶液中,在80℃水浴下加热30min,然后用去离子水清洗,并用烘箱烘干备用;(2) 采用OXFORD-NGP80 DEP薄膜沉积设备,在烘干后的硅片上单面沉积氮化硅薄膜。采用同样的步骤制备二氧化硅薄膜。然后用光谱椭偏仪分别测得沉积氮化硅薄膜厚度为53.4±0.1nm,二氧化硅薄膜厚度为48.5±0.1nm。AFM扫描清洗后硅片表面形貌得表面RMS均方根粗糙度均为1nm以下(扫描范围5μm×5μm)。氮化硅和二氧化硅薄膜表面RMS均方根粗糙度均为2nm以下(扫描范围5μm×5μm)。
2 结果与讨论首先,对称结构SiO2-SiO2确定探针表面电势。本实验采用超纯水与分析纯氯化钠配制0.1、0.3、0.8和1 mM 4种不同浓度氯化钠溶液。电导率仪测得溶液pH为5.5左右,电导率分别为11.2、35.4、60.0和115.2μs/cm,通过电导率与浓度关系计算得溶液实际浓度分别为0.09、0.28、0.48和0.93mM。德拜(Debye)长度可由下式近似计算,
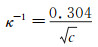 (6)
(6)
式中:c为溶液浓度(mol/L),κ-1为德拜(Debye)长度(nm)。表 1所示为电导率仪(METTLER TOLEDO,SevenMulti S40) 测得上述4种浓度溶液的电导率、实际浓度、德拜(Debye)长度理论值及德拜(Debye)长度实验值对应关系。
| Conductivity(μs·cm-1) | Concentration/mM | Theoretical κ-1/nm | Experimental κ-1/nm |
| 11.2 | 0.09 | 30 | 28 |
| 35.4 | 0.28 | 17 | 19 |
| 94.1 | 0.76 | 11 | 12 |
| 115.2 | 0.93 | 10 | 9 |
AFM接近基底表面过程中主要受静电排斥力和范德华吸引力,将当静电排斥力不足以抵抗范德华吸引力时引起的探针跳变点处作为壁面,也就是距离零点。AFM测得DLVO力曲线如图 5所示:胶体探针距壁面D>100nm时DLVO力主要为0.01~0.1nN的噪音;逐渐靠近壁面,在1.5к-1~3к-1范围内主要是静电力起作用,且以指数衰减;当靠近到距壁面10nm时,范德华力开始显现,随着到壁面距离的进一步减小,影响逐渐明显。在1κ-1范围内,对0.09mM浓度的溶液,DLVO力在6~10nN之间,而0.93mM的在2~5nN之间,主要是因为表面电势及表面电荷密度随着溶液浓度的增大而减小,导致静电排斥力减小。表面电势的求解主要由1.5κ-1~3κ-1范围决定,由图可知此范围内实验数据与理论值拟合较好,也与Ducker[17]及Horn[18]等人的实验结果一致性较好。从图中还可明显看出,DLVO理论拟合曲线在距离壁面1.5κ-1内与实验曲线相比存在一定偏差,此现象在前人实验中也被发现[16]。原因主要是公式(3) 中静电力的理论值是基于Poisson-Boltzmann方程的线性解,会在距离壁面较近的位置存在一定的偏差;同时,在大表面电势的稀浓度溶液中该偏差也明显更大。
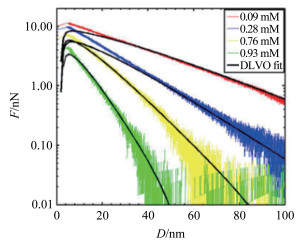
|
| 图 5 二氧化硅基底上胶体探针在4种不同浓度氯化钠溶液下的对数坐标力曲线,黑线为连续电势假设下的PB方程拟合线 Fig.5 Force curves between the colloidal probe and silica in different NaCl concentrations. The black curves are fitted based on PB equation under the assumption of constant potential |
图 6所示为胶体探针表面电势与溶液浓度关系。由图可知,表面电势ψ与pC呈线性关系ψ= -28.98×pC +55.21,与Kirby[4]给出的线性理论相近(pC=-log10C, C为浓度)。本实验在与Ducker[17]及Horn[18]相似的实验条件下,结果与其也较为接近。二氧化硅表面电荷主要是由硅烷醇基电离产生的负电荷,吸附溶液中的阳离子(氢离子和钠离子),中和部分表面电荷,液相剩余的净电荷与固相形成电位差,即表面电势。体溶液中的电势为零电势点,那么样品表面电势为负值。因此,随着溶液浓度的增加(对应pC减小),表面电势绝对值减小。表面电势测量误差通常在±5~10mV以内,一般认为是由胶体探针表面及基底表面粗糙度、胶体探针弹性系数标定误差及AFM系统误差及外界噪声干扰等因素造成。
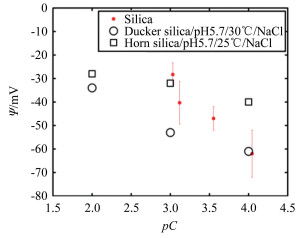
|
| 图 6 二氧化硅表面电势测量结果(红点)及与Ducker(圆圈)和Horn(矩形)在相似测量环境下的结果比较。pC=-lgC(C为溶液浓度) Fig.6 Comparison of the surface potential on silica (red symbols) between Duckers' (circles) and Horns' (squares) under similar experiment conditions. pC=-lgC.(C is concentration) |
图 7所示为硅、二氧化硅及氮化硅表面电势对比图。一般认为,由于硅表面易被氧化,硅与二氧化硅液固表面都是同样排布的硅烷醇基。因此,实验测得硅和二氧化硅在氯化钠溶液中表面电势及表面电荷密度相同。而氮化硅表面电势绝对值比硅和二氧化硅的小10~20mV左右。推测其原因为:硅基样品表面电荷主要是由于硅烷醇基的电离产生。单位面积内氮化硅表面所带硅烷醇基比二氧化硅少[19],浓度等环境一致的条件下,氮化硅表面比二氧化硅表面剩余净电荷少,因此,表面电势绝对值也较小。
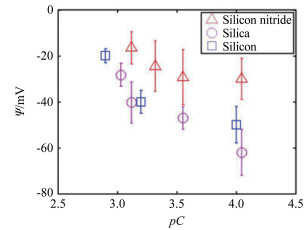
|
| 图 7 硅、二氧化硅和氮化硅表面电势对比 Fig.7 Comparison of surface potentials on silicon, silica and silicon nitride |
本文详细介绍了胶体探针的制作过程及其弹性系数标定方法,通过AFM胶体探针测量系统测量了不同硅基表面液固界面的DLVO力,从而间接测量了表面电势及表面电荷密度,主要结论如下:
(1) AFM胶体探针技术可以很好地测量出静电力的指数衰减段,并可以单独由此段力曲线确定德拜长度,表征静电作用的特征。通过DLVO理论拟合实验曲线可以得到表面电势,表面电荷密度等重要参数。考虑到PB方程的适用性以及静电作用主导的强弱,0.1~1mM浓度是该技术的最优测量范围。
(2) 硅和二氧化硅在条件相同下表面电势绝对值较为接近,而氮化硅要小10~20mV,原因主要是单位面积内氮化硅表面所带硅烷醇基比二氧化硅少,导致在浓度等环境一致的条件下氮化硅表面比二氧化硅表面剩余电荷少,因此,表面电势绝对值也较小。此结果表明,可以通过选取不同硅烷醇基密度的材料来有效调控表面电势,从而在硅基材料的微流控芯片中调控电动流动的强弱。
| [1] | Israelachvili J N. Intermolecular and surface forces[M]. Academic Press, 2011. |
| [2] | 李战华, 吴健康, 胡国庆, 等. 微流控芯片中的流体流动[M]. 北京: 科学出版社, 2012. Li Z H, Wu J K, Hu G Q, et al. Fluid flow in microfluidic chips[M]. Beijing: Science Press, 2012. |
| [3] | 林炳承, 秦建华. 图解微流控芯片实验室[M]. 北京: 科学出版社, 2008. Lin B C, Qin J H. Graphic laboratory on a microfluidic chip[M]. Beijing: Science Press, 2008. |
| [4] | Kirby B J, Hasselbrink E F. Zeta potential of microfluidic substrates:Theory, experimental techniques, and effects on separations[J]. Electrophoresis, 2004, 25(2): 187–202. DOI:10.1002/(ISSN)1522-2683 |
| [5] | Schoch R, Han J, Renaud P. Transport phenomena in nanofluidics[J]. Review of Modern Physics, 2008, 80(3): 839–883. DOI:10.1103/RevModPhys.80.839 |
| [6] | Butt H J, Cappella B, Kappl M. Force measurements with the atomic force microscope:technique, interpretation and applications[J]. Surface Science Reports, 2005, 59(1-6): 1–152. DOI:10.1016/j.surfrep.2005.08.003 |
| [7] | Audry M C, Piednoir A, Joseph P, et al. Amplification of electro-osmotic flows by wall slippage:direct measurements on OTS surfaces[J]. Faraday Discussions, 2010, 146(146): 113–124. |
| [8] | 郝旭欢, 常博, 郝旭丽. MEMS传感器的发展现状及应用综述[J]. 无线互联科技, 2016, 3: 95–96. Hao X H, Chang B, Hao X L. Current development and application of MEMS sensors[J]. Wireless Internet Technology, 2016, 3: 95–96. DOI:10.3969/j.issn.1672-6944.2016.03.042 |
| [9] | Horn R G, Vinogradova O I, Mackay M E, et al. Hydrodynamic slippage inferred from thin film drainage measurements in a solution of nonadsorbing polymer[J]. Journal of Chemical Physics, 2000, 112(14): 6424–6433. DOI:10.1063/1.481274 |
| [10] | Van Zwol P J, Palasantzas G, Van de Schootbrugge M, et al. Roughness of microspheres for force measurements[J]. Langmuir, 2008, 24(14): 7528–7531. DOI:10.1021/la800664f |
| [11] | Sader J E, Larson I, Mulvaney P, et al. Method for the calibration of atomic force microscope cantilevers[J]. Review of Scientific Instruments, 1995, 66(7): 3789–3798. DOI:10.1063/1.1145439 |
| [12] | Butt H J, Jaschke M. Calculation of thermal noise in atomic force microscopy[J]. Nanotechnology, 1995, 6(1): 1–7. DOI:10.1088/0957-4484/6/1/001 |
| [13] | Sader J E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope[J]. Journal of Applied Physics, 1998, 84(1): 64–76. DOI:10.1063/1.368002 |
| [14] | Sader J E, Chon J W M, Mulvaney P. Calibration of rectangular atomic force microscope cantilevers[J]. Review of Scientific Instruments, 1999, 70(10): 3967–3969. DOI:10.1063/1.1150021 |
| [15] | Cleveland J P, Manne S, Bocek S, et al. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy[J]. Review of Scientific Instruments, 1993, 64(2): 403–405. DOI:10.1063/1.1144209 |
| [16] | Kuznetsov V, Papastavrou G. Ion adsorption on modified electrodes as determined by direct force measurements under potentiostatic control[J]. The Journal of Chemical Physics C, 2014, 118(5): 2673–2685. DOI:10.1021/jp500425g |
| [17] | Ducker W A, Senden T J, Pashley R M. Direct measurement of colloidal forces using an atomic force microscope[J]. Nature, 1991, 353(353): 239–241. |
| [18] | Horn R G, Smith D T. Measuring surface forces to explore surface chemistry:Mica, sapphire and silica[J]. Journal of Non-Crystalline Solids, 1990, 120(1-3): 72–81. DOI:10.1016/0022-3093(90)90192-O |
| [19] | Legrand P A. The surface properties of silicas[J]. International Journal of Food Science & Technology, 2015, 50(4): 966–973. |



