2. 中国水利水电科学研究院, 北京 100038
2. China Institute of Water Resources and Hydropower Research, Beijing 100038, China
液滴融合现象广泛存在于自然界及工业生产中,在海洋石油污染处理、微流控技术等领域中起关键作用,深入认识其机理和掌握相关共性规律无疑有着重要的应用价值[1-2]。
准静态液滴融合,即不考虑液滴相互靠近过程对融合过程带来的影响,是目前基础研究的热点[3-10]。当液滴以较快的速度碰并融合时,液滴靠近的过程对融合有着显著的影响,对此国内外亦有很多相关研究[11-12]。确定液滴靠近过程对融合过程的影响,进而准确划分准静态融合与碰并融合的界限,对于深化认识液滴融合的物理机制有着重要的意义。
当两液滴在液体环境中以一定的速度靠近、接触时,液滴会相互挤压产生变形,在接触的区域形成一层微小液膜。液膜逐渐变薄到一定程度时,融合从液膜上一点开始,形成连接两液滴的通道,称为液桥。液桥形成后持续扩张并拉动两液滴融为一体。对液桥扩张规律的研究一直是此前准静态液滴融合研究的重点。根据Paulsen[13-16]等用电测法测量的结果,在液滴准静态融合情况下,融合初期液桥半径与时间t成正比,满足粘性力、惯性力与表面张力共同作用的ILV(Inertially Limited Viscous)机制,融合后期液桥半径与t0.5成正比,且根据液体粘度的高低,分别满足由惯性力或粘性力主导的机制。然而当液滴靠近速度增大到一定程度时,融合中液桥半径的增长规律发生突变,电测法测得的融合初期等效液桥半径与t0.72成正比增长[14]。说明此时融合的物理机制发生了变化,且与融合前的靠近过程有关。因此需要探究准静态融合的条件,即融合规律发生突变的临界靠近速度。这就要求从正面来直接观察液桥的形态,而以目前的电测法或侧视拍摄的方法,都难以直观认识液桥截面的形态。此外,液滴融合过程的时间尺度依赖于液滴半径[16],选取大尺寸的液滴可以延缓液滴融合的进程,更有利于对融合过程的观测。然而受制于传统的悬吊式方法很难产生大尺寸液滴,目前大部分研究仍着眼于半径为毫米量级的小液滴。
基于以上考虑,本文采用一种能产生较大尺寸液滴的实验装置,通过顶视高速阴影法,直接观测液桥截面的形态变化。比较不同靠近速度下融合起始点位置、液桥截面形态的差异,提取融合过程发生突变的临界靠近速度,旨在分析融合前接触变形对融合过程的影响。
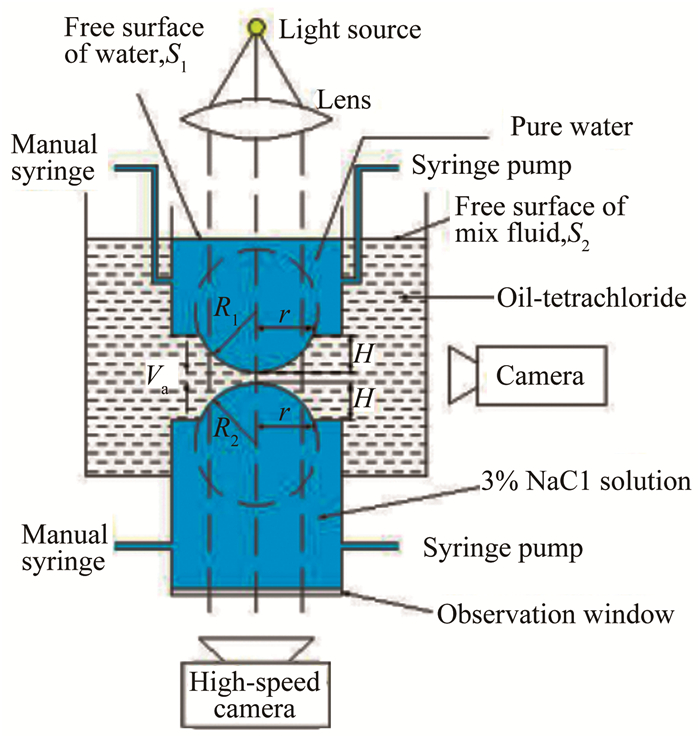
1 实验方法和装置实验装置[17]如图 1所示,分为上圆筒、下圆筒和方形外盒3个部分,分别盛装上层内液、下层内液和外液。3种液体分别使用纯水、3%NaCl水溶液和白油四氯化碳混合溶液,内外液不混溶,调节各部分液体密度使ρ上 < ρ外 < ρ下, 且密度差小于2%,构建准失重环境,使液滴形成近似理想球状。通过注射泵驱动向上下圆筒中注入相应的液体,两圆筒端面圆孔处即可形成局部模拟两液滴靠近的球形冠部,而两“液滴”的另外一侧则分别被上自由面和下透明玻璃板“削平”,从而可采用顶视方法观测上下液滴接触以及发生融合的过程。另外,侧视拍摄仍可采用前人类似方法记录融合前液滴靠近接触形貌。通过控制注射泵的注入量,可以精确控制液滴的靠近速度,液滴靠近速度va与注入流量满足关系[18]:
|
| 图 1 实验装置原理图 Fig.1 Schematic of experimental setup |
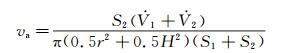 (1)
(1)
式中: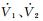
传统的侧视方法受到液滴表面遮挡和散射效果的影响,初期的微小液桥难以捕捉,同时侧视法得到的仅是液桥的圆形外部轮廓,而难以捕捉到真实的截面形态。本文通过高速摄影顶视阴影法(见图 1),可以清晰地观测到融合起始点的位置、融合过程中液桥截面形态的变化和液桥中心的位置,并计算得到融合过程中液桥中心的偏移。
为分离靠近速度和接触变形的影响,一方面通过改变微流泵注入的液体流量来获取不同的液滴靠近速度,直接探究液滴靠近速度对融合的影响。另一方面,通过控制注射器快速注入液体,使液滴产生明显的接触变形后静置待其融合,结合侧视拍摄,记录液滴融合前的接触变形,通过这种方法,直接探究液滴融合前的接触变形对融合的影响。
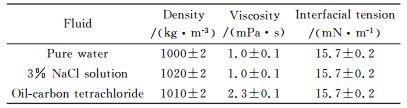
本文采用浮子密度计和毛细管粘度计分别测量液滴和环境液体的密度和粘度,通过悬滴法测得液滴与环境液体之间的界面张力。测量得到的相关物性参数如表 1所示。
进行了一系列不同靠近速度条件下的液滴融合实验,靠近速度变化范围为10-7~10-5m/s。实验中观察到,随着靠近速度的变化,液滴融合过程会出现2种典型模式,本文根据其几何形状的变化特征,暂且称之为圆形融合和形变融合。
图 2和3分别给出了圆形融合和形变融合过程的典型高速摄影图片,液滴等效半径均为R=1.0cm,图中每个像素对应45μm,靠近速度分别为1.8×10-6和5.4×10-6m/s。靠近速度较低时,融合前平行光透过2球形液滴形成光强渐变的区域,如图 2(a)所示。依据液桥边缘的形态,融合可分为初期和后期2个阶段:初期融合从一点开始,图像上只有1条表示液桥边缘的暗环,保持规则圆形向外扩张,如图 2(b)和(c)所示;后期则交替出现多条同心的亮暗圆环,与液桥同步扩张,如图 2(f)、(g)、(h)和(i)所示。两者之间的转变大约出现在t=0.4ms时,此刻表征液桥边缘的1条暗纹开始逐渐向多条转变,如图 2(d)和(e)所示,整个过程液桥截面一直保持圆形向外扩展,即呈现圆形融合的特征。当靠近速度较高时,融合开始前光斑中心存在1个光强均匀的高亮度区域,如图 3(a)所示,这是由于液滴挤压变形形成扁平区域,光线在此区域均匀透射所致。依据液桥截面的形态,融合可分为初期、中期和后期3个阶段:初期融合从靠近高亮区域边缘处开始,在较短时间内液桥以规则圆形扩张,如图 3(b)和(c)所示。大约t=0.4ms时, 融合进入中期阶段,液桥边缘远离接触区域中心的一侧扩张速度显著变慢,液桥截面由规则圆形转变为两圆交集,如图 3(d)、(e)和(f)所示。本文将液桥边缘远离接触区域中心的一侧称为外侧边界,另一侧称为内侧边界。外侧边界扩张时,逐渐由1条暗纹向多条明暗相间的条纹转变,内侧边界则一直保持1条暗纹扩张。在t=2ms时,内外侧边界逐渐重合,构成1个完整的圆形,此后液桥扩张形态与低靠近速度融合后期一致,如图 3(g)、(h)和(i)所示。鉴于该融合过程中液桥截面形状不断改变,暂将其称之为形变融合。

|
| 图 2 较低靠近速度下圆形融合过程 Fig.2 The coalescing process at lower approaching speed |

|
| 图 3 较高靠近速度下形变融合过程 Fig.3 The coalescing process at higher approaching speed |
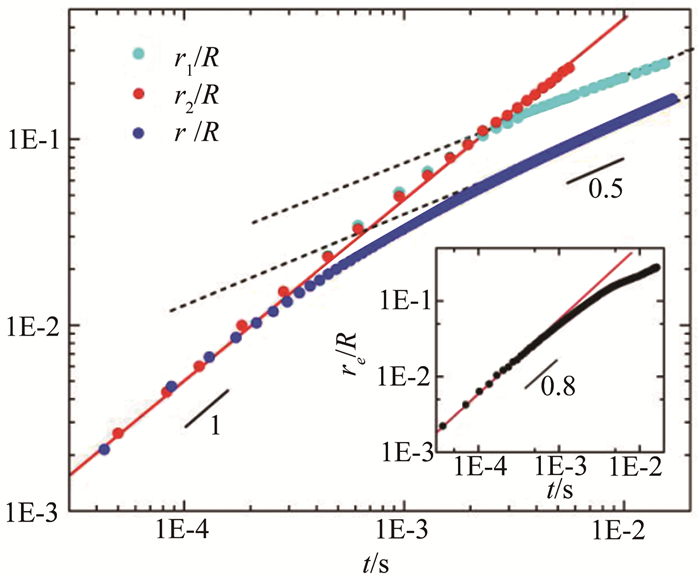
从融合过程图像中提取液桥边缘,分别得到上述2种情况下液桥半径在双对数坐标下随时间增长的曲线,如图 4所示。曲线所示靠近速度分别为1.6×10-7和1.6×10-5m/s,作为圆形融合和形变融合的演变规律示例。r为圆形融合的液桥半径,r1和r2分别为形变融合过程中两圆交集的外侧和内侧边界对应半径,re则为其等效液桥半径。
|
| 图 4 液桥半径随时间变化关系 Fig.4 Liquid bridge radius versus time |
图 4中蓝色线表示圆形融合液桥无量纲半径随时间的变化关系。曲线在双对数坐标下呈现出2个特征段。融合初期,r(t)/R与t成正比,融合后期,与t0.5成正比。此前用光测和电测等方法进行的准静态液滴融合研究已经基本确定了这2个阶段的物理机制和规律[16, 19]。在液桥扩张的最初阶段,上下液滴界面在垂直方向的距离很小,表面张力作用显著,液桥扩张符合表面张力与粘性力、惯性力共同作用的ILV机制,液桥半径与t成正比增长;随着液桥扩张,界面垂直距离增大,表面张力作用减弱,根据外液粘度高低,粘性力或惯性力起主导作用,液桥扩张进入粘性机制或惯性机制(本文工况下为惯性机制),液桥半径与t0.5成正比增长。本文结果与过去已有方法所得结果一致,表明该条件下液滴为准静态融合。
而当靠近速度较高出现形变融合时,融合的机制和过程发生改变。图 4中红色和青色曲线分别表示较高靠近速度下液桥内侧和外侧边界圆弧无量纲半径随时间的增长规律。由于融合中期液桥是两圆交集,因此分别提取液桥内外两侧边界,通过圆弧拟合得到对应半径,其中外侧边界用青色圆r1标记,内侧边界用红色圆r2标记,如图 3(f)所示。融合初期液桥保持规则圆形,内外侧边界难以区分,液桥半径与t成正比增长。融合中期液桥逐渐变为由内外侧边界组成的非规则圆形,两侧边界圆弧半径以不同规律增长, 两曲线逐渐分离。外侧边界对应半径r1与t0.5成正比增长,与低靠近速度下融合后期液桥增长规律一致;内侧边界对应半径r2与t成正比增长,与初期规律一致。后期内侧边界逐渐消失,外侧边界构成完整圆形,增长规律不变。
有意思的是,若取与非规则液桥面积相同的圆的半径为等效液桥半径re,其随时间的变化如图 4中插图所示。对应于融合的初期和中期,曲线在双对数坐标下拟合斜率约为0.8,即re近似与t0.8成正比增长。这与Paulsen等以电测法测得的较高靠近速度下融合等效液桥半径与t0.72成正比增长[14]相近。因此可以说明,由电测法测得的介于0.5和1之间的指数规律,是由于融合中期液桥不是规则圆形,液桥两侧边界扩张遵循不同的机制所致。融合从靠近液膜边缘处一点开始后,在较短的时间内液桥以规则圆形在液膜范围内扩张。由于液膜厚度很小且基本均匀,因此这段时间内液桥扩张遵循ILV机制,液桥半径与t成正比增长。而当液桥边缘远离液膜中心点的一侧(外侧边界)率先到达液膜边缘时,这一侧的液桥扩张速度会显著变慢,不过另一侧(内侧边界)却基本不受影响,仍以原速度扩张,液桥截面形态变为两圆交集。外侧边界超出原液膜范围后,上下液滴界面在垂直方向的距离急剧增加,因此液桥扩张的物理机制由ILV机制转变为惯性机制,外侧边界对应半径从与t成正比转变为与t0.5成正比增长。与此同时,内侧边界仍在液膜范围内扩张,遵循ILV机制。直到内外侧边界逐渐重合后,液桥逐渐恢复轴对称性,最终半径趋于t0.5的规律增长。这就合理地解释了前人所纠结的液桥半径与t0.72成比例增长[14]的疑惑。
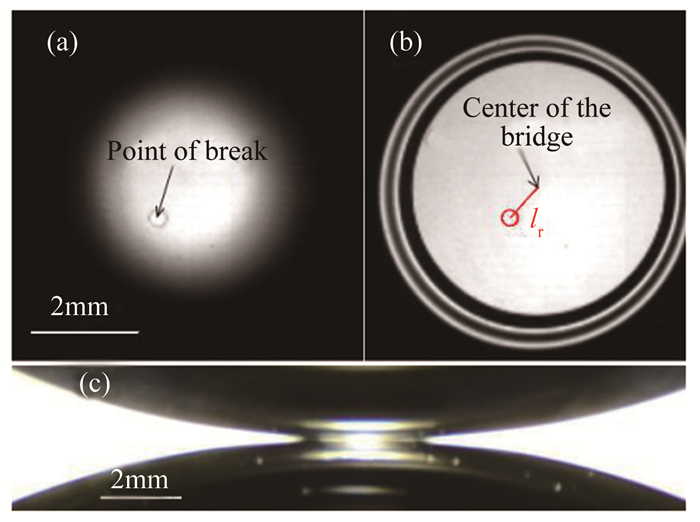
2.2 接触变形对融合过程的影响除了融合规律不同,2种融合过程起始点的位置也有明显区别。圆形融合时,融合起始点与后续过程液桥中心几乎一直重合,即液桥扩张过程中中心位置几乎不变;而形变融合时,融合起始点则在挤压变平形成的高亮区域边缘附近,液桥扩张过程中,其几何中心位置在不断变化,直到最终液桥变为规则圆形后保持不变。为比较靠近速度对融合起始位置的影响,定义融合过程中某时刻液桥中心到融合起始点的距离为该时刻的液桥中心偏移l,而融合后期液桥保持圆对称时的液桥中心位置到融合起始点的距离为液桥最大中心偏移lr,如图 5(a)和(b)所示。
|
| 图 5 液桥中心偏移与融合前接触变形示意图 Fig.5 The displacement of bridge center and drop deformation before coalescence |
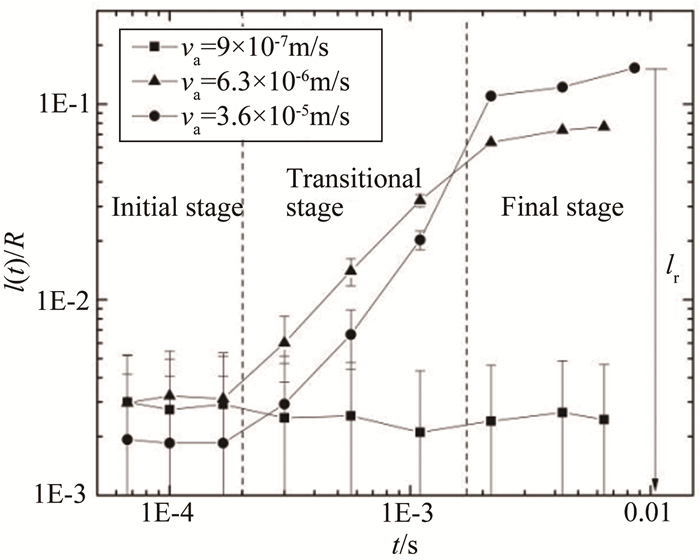
图 6统计了不同靠近速度下液桥中心偏移l随时间t的变化,采用形心作为非规则圆形液桥的中心。当靠近速度较低时,液桥中心偏移l在测量误差范围内波动,可认为融合自液滴接触的正中心开始。当靠近速度较高时,融合前期l基本为0;融合中期l经历一个增长过程,此时,液桥内外两侧圆弧无量纲半径随时间的增长规律产生差异,使液桥形心产生偏移;而融合后期液桥又成为规则的圆形,中心偏移不再继续增大,圆心位置保持稳定。从图 6中也可以提取出不同靠近速度下的液桥中心最大偏移距离lr。
|
| 图 6 不同靠近速度下液桥中心偏移曲线 Fig.6 The displacement of liquid bridge center versus time with different approaching speeds |
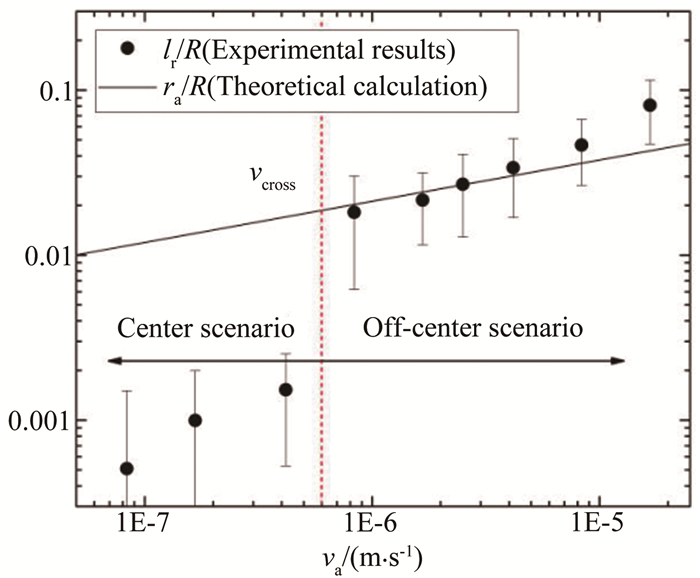
将液桥中心最大偏移lr与根据液滴正碰理论[20]得到的接触变形液膜半径ra进行比较,如图 7所示。其中ra与液滴靠近速度va的关系为:
|
| 图 7 不同靠近速度下液桥最大中心偏移与理论液膜半径关系 Fig.7 The displacement of bridge center and theoretical bridge radius versus approaching speed |
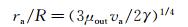 (2)
(2)
式中:μout为环境流体粘性系数;γ为界面张力系数。
从图中可以看出,当靠近速度较高时,lr与ra较为吻合,说明融合起始点在靠近液膜边缘处。而当靠近速度小到一定程度时,lr突然变小,远小于对应的理论液膜半径。本文定义此突变对应的速度为临界靠近速度vcross。当va < vcross时,lr在图像上对应的幅值小于一个像素,与测量误差同量级,且比此时理论预测液膜半径小约一个数量级。因此可以认为液桥中心偏移几乎为0,即融合起始点在接触面中心处,且与靠近速度无关。此临界靠近速度可作为判断准静态融合的依据,也就是说,在有环境流体存在的情况下,当液滴靠近速度小于临界靠近速度时,液滴融合起始位置与靠近速度无关,融合过程不受靠近过程影响。反之,融合的过程则同液滴靠近的过程及其带来的影响相关。
由以上分析,以临界靠近速度为界,可以将融合过程分为2种模式:低靠近速度下的中心融合模式和高靠近速度下的边缘融合模式。2种融合模式的差异如前所述,其中中心融合可以认为是准静态融合。另外,实验中发现,在临界靠近速度附近融合模式呈现一定的随机性[21]。
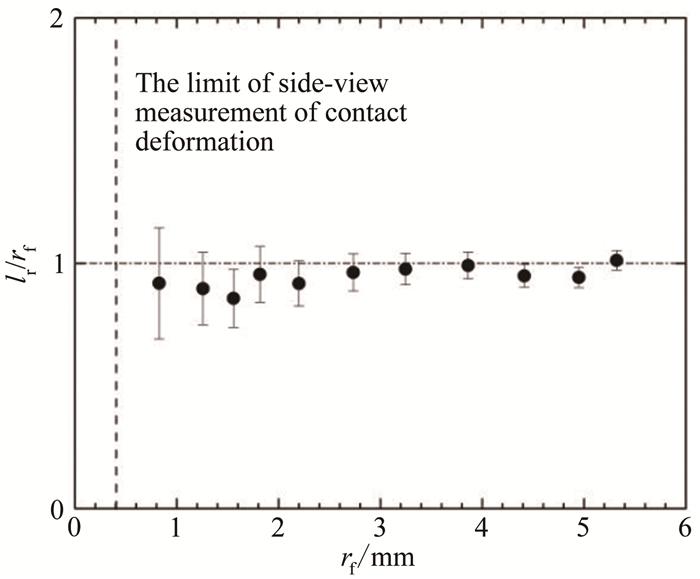
当靠近速度较高时,液滴发生明显变形,并在接触区域形成环境流体液膜。为确定融合前实际液膜大小与融合后液桥中心最大偏移的关系,本文还刻意增加了接触变形的影响实验。具体做法是,大幅提升注射速度使液滴快速靠近并产生某一确定程度的接触变形后静置待其融合,然后同时从侧视和顶视角度进行拍摄。图 5为侧视与顶视照片对比图,侧视为普通相机拍摄,顶视为高速摄影拍摄。从普通相机侧拍的融合前瞬间的照片中提取接触面大小,记为实际液膜半径rf, 以衡量接触变形的程度, 如图 5(c)所示。从高速摄影顶视拍摄照片中提取液桥最大中心偏移lr,将rf与lr进行对比,结果如图 8所示。从图中可以看出,在不同的初始液膜半径下,lr均与rf较为符合。说明液滴有明显接触变形时,融合起始点在靠近液膜边缘处,lr可以在一定程度上衡量融合前挤压变形产生液膜的大小,并且此时液滴融合的形态符合高靠近速度下的边缘融合模式。左端虚线给出了接触面侧面拍摄可分辨的最小液膜半径,约为0.4mm。当接触面半径小于此极限时,侧视手段难以判断液滴是否有变形。
|
| 图 8 实际液膜半径rf与液桥最大中心偏移lr关系 Fig.8 The radius of liquid film rf versus the displacement of bridge center lr |
液滴融合存在边缘融合和中心融合2种典型融合模式。当靠近速度大于某一临界速度时,液滴融合自液滴相互挤压形成的环境流体液膜边缘开始,融合过程中液桥截面并非规则圆形,而是两圆交集,且两部分液桥扩张速度有差异,造成液桥扩展过程中形状的改变和几何中心的偏移。反之,当靠近速度小于相应的临界速度时,融合则从两液滴顶端开始,液桥截面始终保持规则圆形,且融合过程中液桥中心位置恒定,此时融合过程与靠近速度无关,呈准静态融合特征。
| [1] | 陈晓东, 胡国庆. 微流控器件中的多相流动[J]. 力学进展, 2015, 45: 55–110. Chen X D, Hu G Q. Multiphase flow in microfluidic devices[J]. Advances in Mechanics, 2015, 45: 55–110. |
| [2] | 申峰, 李易, 刘赵淼, 等. 基于微流控技术的微液滴融合研究进展[J]. 分析化学, 2015, 43(12): 1942–1954. Shen F, Li Y, Liu Z M, et al. Advances in micro-droplets coalescence using microfluidics[J]. Chinese Journal of Analytical Chemistry, 2015, 43(12): 1942–1954. DOI:10.11895/j.issn.0253-3820.100509 |
| [3] | Sprittles J E, Shikhmurzaev Y D. Coalescence of liquid drops: different models versus experiment[J]. Physics of Fluids, 2012, 24(12): 122105. DOI:10.1063/1.4773067 |
| [4] | Sprittles J E, Shikhmurzaev Y D. Dynamics of liquid drops coalescing in the inertial regime[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2014, 89(6): 063008. DOI:10.1103/PhysRevE.89.063008 |
| [5] | Sprittles J E, Shikhmurzaev Y D. The coalescence of liquid drops in a viscous fluid: interface formation model[J]. Journal of Fluid Mechanics, 2014, 751: 480–499. DOI:10.1017/jfm.2014.313 |
| [6] | Sprittles J E, Shikhmurzaev Y D. A parametric study of the coalescence of liquid drops in a viscous gas[J]. Journal of Fluid Mechanics, 2014, 753: 279–306. DOI:10.1017/jfm.2014.362 |
| [7] | Thoroddsen S, Etoh T, Takehara K. High-speed imaging of drops and bubbles[J]. Annu Rev Fluid Mech, 2008, 40: 257–85. DOI:10.1146/annurev.fluid.40.111406.102215 |
| [8] | Kavehpour H P. Coalescence of drops[J]. Annual Review of Fluid Mechanics, 2015, 47(1): 245–268. DOI:10.1146/annurev-fluid-010814-014720 |
| [9] | Baroudi L, Nagel S R, Morris J F, et al. Dynamics of viscous coalescing droplets in a saturated vapor phase[J]. Physics of Fluids, 2015, 27(12): 121702. DOI:10.1063/1.4936942 |
| [10] | Pothier J C, Lewis L J. Molecular-dynamics study of the viscous to inertial crossover in nanodroplet coalescence[J]. Physical Review B, 2012, 85(11): 115447. DOI:10.1103/PhysRevB.85.115447 |
| [11] | 刘栋. 液滴碰撞及其融合过程的数值模拟研究[D]. 北京: 清华大学, 2013. Liu D. Numerical simulations on collision and coalescence of binary droplets[D]. Beijing: Tsinghua University, 2013. |
| [12] | Tang C, Zhang P, Law C K. Bouncing, coalescence, and separation in head-on collision of unequal-size droplets[J]. Physics of Fluids, 2012, 24(2): 022101. DOI:10.1063/1.3679165 |
| [13] | Paulsen J D, Burton J C, Nagel S R. Viscous to inertial crossover in liquid drop coalescence[J]. Phys Rev Lett, 2011, 106(11): 114501. DOI:10.1103/PhysRevLett.106.114501 |
| [14] | Paulsen J D, Burton J C, Nagel S R, et al. The inexorable resistance of inertia determines the initial regime of drop coalescence[J]. Proc Natl Acad Sci U S A, 2012, 109(18): 6857–6861. DOI:10.1073/pnas.1120775109 |
| [15] | Paulsen J D. Approach and coalescence of liquid drops in air[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2013, 88(6): 063010. DOI:10.1103/PhysRevE.88.063010 |
| [16] | Paulsen J D, Carmigniani R, Kannan A, et al. Coalescence of bubbles and drops in an outer fluid[J]. Nat Commun, 2014, 5: 3182. |
| [17] | Wang L, Zhang G, Wu H, et al. Note: a top-view optical approach for observing the coalescence of liquid drops[J]. Rev Sci Instrum, 2016, 87(2): 026103. DOI:10.1063/1.4941778 |
| [18] | 王鲁海. 复杂管流条件下涡轮流量计响应规律及多相影响研究[D]. 合肥: 中国科学技术大学, 2016. Wang L H. The response characteristics of flowmeter in complex and multiphase flow conditions[D]. Hefei: University of Science and Technology of China, 2016. |
| [19] | Fezzaa K, Wang Y. Ultrafast x-ray phase-contrast imaging of the initial coalescence phase of two water droplets[J]. Phys Rev Lett, 2008, 100(10): 104501. DOI:10.1103/PhysRevLett.100.104501 |
| [20] | Zhang P, Law C K. An analysis of head-on droplet collision with large deformation in gaseous medium[J]. Physics of Fluids, 2011, 23(4): 042102. DOI:10.1063/1.3580754 |
| [21] | Case S C. Coalescence of low-viscosity fluids in air[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2009, 79(2): 026307. DOI:10.1103/PhysRevE.79.026307 |