2. 河海大学 港口海岸与近海工程学院, 南京 210098;
3. 水文水资源与水利工程科学国家重点实验室, 南京 210098;
4. 港口航道泥沙工程交通行业重点实验室, 南京 210024
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. The State Key Laboratory of Hydrology-water Resources and Hydraulic Engineering, Nanjing 210098, China;
4. Key Laboratory of Port, Waterway and Sedimentation Engineering of Ministry of Transport, Nanjing 210024, China
在河口海岸工程的研究与应用中,水下泥沙输移与底部剪应力大小直接相关,因此底部剪应力是研究泥沙运动基础理论的重要途径之一。由于河口海岸工程研究中的水下底部剪应力量级小、测量环境恶劣和水动力条件复杂[1]等原因,其底部剪应力的难以测量在一定程度上制约了泥沙运动理论的发展。随着微机电系统(Microelectromechanical Systems,MEMS)技术的发展,出现了基于MEMS技术的微型壁面剪应力传感器,例如浮动式剪应力传感器[2]、格栅式剪应力传感器[3-4]和柔性热膜式剪应力传感器[5-6]等,其中柔性热膜式剪应力传感器适宜在水下应用。相对于河口海岸工程研究中较多采用的应力板[7-8],热膜式壁面剪应力传感器具有对流场的干扰小、时空分辨率高,以及可以测量微小剪应力等优点,显示了其广阔的应用前景。
传感器的准确标定是传感器特性研究与应用的前提。热式壁面剪应力传感器对环境介质的温度十分敏感[9-11],为了研究环境温度对壁面剪应力传感器工作的影响,开展不同环境温度下的壁面剪应力传感器标定十分重要。目前壁面剪应力传感器的标定与应用大多集中在空气介质中,而水下壁面剪应力传感器标定装置的研究较少[12-14],并且已有的水下标定装置并没有考虑水体温度的可变性。
本文总结已有的水下标定方法,基于宽扁管道内壁面剪应力与沿程压力梯度的关系研制了一种水下壁面剪应力传感器温控标定装置,可以实现不同水温条件下的壁面剪应力传感器静态标定,并进行了MEMS柔性热膜式壁面剪应力传感器在不同水温条件下的标定实验。该装置本质上是一种具有温控功能的水下标准剪应力输出装置,并不限于热式壁面剪应力传感器的标定,可为各种类型的水下壁面剪应力传感器的研究和应用提供基础。
1 水下标定方法壁面剪应力传感器的标定即通过标定装置输出一系列壁面剪应力,再将其与传感器输出的相应电信号进行对比从而建立标定关系供研究和应用。对于热膜式壁面剪应力传感器,一般输出的电信号为电压值E,因此标定即建立标定装置输出的壁面剪应力τ和传感器输出电压值E之间的标定关系。
根据牛顿内摩擦定律,壁面剪应力τ与近壁面流速的法向梯度du/dy存在如下关系:
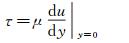 (1)
(1)
式中:μ为动力粘性系数;u为流速。获得壁面剪应力最直接的方法是准确测量获得近壁处流速的法向梯度。对于层流流动,流速的方向梯度可以很容易通过测量获得。对于紊流流动,流速仅在粘性底层内为法向上线性分布,而粘性底层很薄,会导致测量上的困难。因此可通过测量流速、流量和压力损失等量来间接获得壁面剪应力的大小。
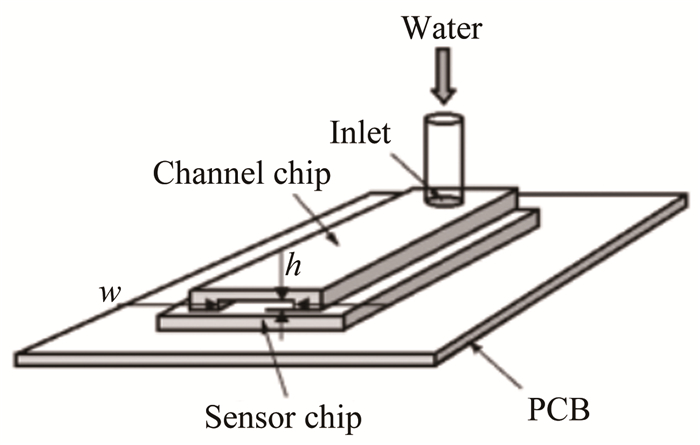
目前水下标定中常用的标定装置是微型宽扁管道层流标定装置[11-13],如图 1所示。在高度为微米至毫米级的微型宽扁管道层流中,流量Q与壁面剪应力τ存在如下关系:
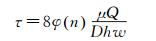 (2)
(2)
式中:D为微型管道水力直径;h为微型宽扁管道高度;w为微型宽扁管道宽度;φ(n)为与h/w相关的形状修正系数。该方法只需测量流量Q即可计算壁面剪应力,但其最大的限制在于壁面剪应力计算公式(2) 仅适用于层流流动,因此该标定装置所能提供的最大剪应力有限。再者,由于微型管道的高度非常小,此时壁面剪应力传感器本身厚度和微型管道的加工精度对流动的影响也需要考虑。
徐华[15]根据矩形宽扁管道内的流速分布公式,推导了断面平均流速U与摩阻流速u*间的关系,再根据τ=ρu*2计算壁面剪应力,由于采用的流速分布公式仅限于紊流的流速分布,因此该方法仍有一定的局限性。宽扁管道内边壁的存在对主流流速分布也存在影响。
对于2块无限宽平行平板间充分发展的二维流动,其沿程的压力梯度不变,壁面剪应力τ与沿程压力梯度Δp/Δx存在如下关系:
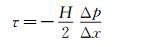 (3)
(3)
式中:H为平板间的间距。由于无限宽的平板在实际中是不存在的,可采用较大宽高比的矩形断面宽扁管道来近似模拟平行平板间的流动,宽扁管道的高度即为H。公式(3) 与流体的性质无关,并且同时适用于层流和紊流状态[16],只需测量沿程压力梯度即可获得壁面剪应力。田于逵等[14]基于该方法研发了一种可在相对较高雷诺数下进行标定的装置,并对阵列式壁面剪应力传感器阵列进行了水下标定。考虑到水温对热式壁面剪应力传感器工作的影响较大,本文在壁面剪应力与沿程压力梯度关系公式(3) 的基础上,研发一种可控温的水下壁面剪应力传感器标定装置。
2 标定装置设计壁面剪应力与沿程压力梯度关系公式(3) 应用的前提是无限宽平行平板间的流动,但实际中所用的水槽均为有限宽的矩形断面管道。管道两侧的边壁上存在部分壁面剪应力,并且边壁的存在会产生影响主流的二次流,从而影响上下壁面剪应力的横向分布。通常当宽高比大于10:1时可以不考虑边壁对主流区的影响[17],Vinuesa等人[18]采用直接数值模拟(DNS)对矩形断面管道边壁的影响进行了研究,认为宽高比大于24:1时可以不考虑边壁影响。Knight等人[19-20]曾对一系列不同宽高比的宽扁管道内壁面剪应力分布进行过研究,并提出了一种修正公式用于计算宽扁管道内上下壁面中心线上的最大壁面剪应力的值:
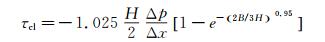 (4)
(4)
式中:τcl为上下壁面中心线上的最大剪应力;B为宽扁管道的宽度;H为宽扁管道的高度。综合考虑到实验场地的大小、水泵提供流量的范围以及量测设备的量程,本标定装置的标定段宽高比为11:1,并采用式(4) 作为标定点处的壁面剪应力计算公式。
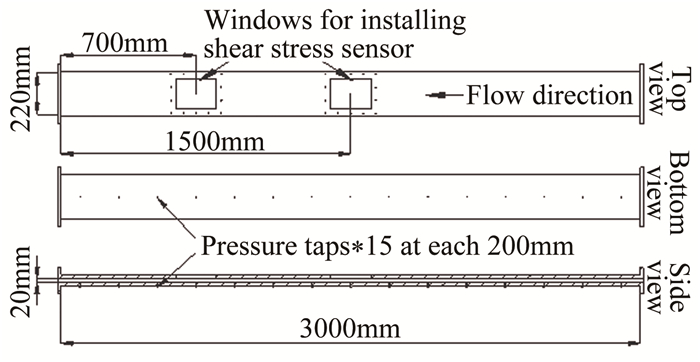
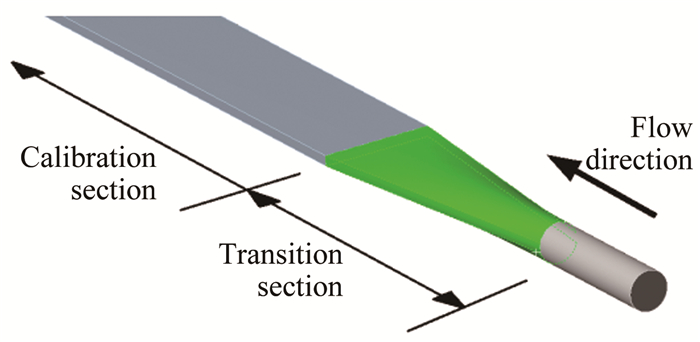
标定装置的标定段宽扁管道长3000mm,宽220mm,高20mm。标定段中心线上沿程每隔200mm开一个测压孔用以测量沿程压力差,共计15个测压孔,可根据压差的大小选择适合的测压孔进行测量,标定段示意图如图 2所示。标定段前后配有长600mm的从圆形截面平滑过渡到矩形截面的过渡段,用于连接水管和标定段,如图 3所示。
|
| 图 2 标定段宽扁管道示意图 Fig.2 Diagrammatic sketch of the calibration section |
|
| 图 3 用于连接水管和标定段的平滑过渡段 Fig.3 Transition section for connecting pipe and calibration section |
管道内的流动需要经过一定距离的发展以后才能变为充分发展的流动,该距离即进口段长度。标定的剪应力传感器安装位置必须位于充分发展段。在进行压差测量时,测点位置也要位于壁面剪应力稳定的位置。矩形截面管道流的进口段长度没有定论[21-22],因此本文采用数值模拟的方法对该设计标定段内的流动进行调查。数值模拟的湍流模式采用k-ω模型,该模型可以较好地模拟近壁处的粘性流动[16],计算网格数为163万。
通过数值模拟,对10、20和30℃这3种水温下4组不同的流量进行计算,获得标定段壁面剪应力τ在标定段内的沿程分布情况,如图 4所示,L表示到入口位置的距离。从模拟结果可以看出,在标定段头部的壁面剪应力沿程分布并不稳定,壁面剪应力需要经过一段距离的发展以后才能达到稳定。在流量为2和10m3/h的情况下壁面剪应力可以很快达到稳定,而在流量为35m3/h时,壁面剪应力在距离入口1.2m以后才能达到稳定。图 4也可为压差测点的选择提供参考。

|
| 图 4 标定段壁面剪应力沿程分布 Fig.4 Distribution of wall shear stress along the calibration section |
根据数值模拟的结果,剪应力传感器的安装窗口设置在距离标定段进口1500mm处,为了提高标定效率,在第1个安装窗口之后800mm还有第2个窗口,可根据需要同时标定2个壁面剪应力传感器。窗口四周预留有密封圈安装槽,可以用硅胶密封圈或者发泡硅胶圈密封,传感器安装在窗口对应的盖板底部,引线从盖板背部引出,引线位置用工业橡皮泥密封,盖板底部与标定段内壁齐平安装。
考虑到后续开展的河口海岸工程应用实验,本次标定装置配置的变频水泵最大流量为35m3/h,对应的最大输出剪应力约为11Pa。标定装置配有电磁流量计和微压差变送器用以监测标定段流量和沿程压力梯度。如果需要进行更大剪应力的标定,只需更换水泵和电磁流量计即可。流量大小可由变频水泵、主管阀门和回水管阀门共同调节。整个标定装置的平面布置图如图 5所示。

|
| 图 5 水下壁面剪应力传感器温控标定装置平面布置图 Fig.5 Layout of the calibration device with temperature control for underwater wall shear stress sensor |
温度控制系统基于PID控制技术,由数据采集器、加热控制器和工控机3部分组成。温度控制系统在实测水温低于设定的标定水温时,会自动控制加热棒进行加热,在实测温度达到设定的标定温度时,会自动停止加热棒加热,温度控制系统继续监测水体温度,如果温度下降超过0.1℃加热棒就继续加热。该温度控制系统可保证水箱内水温不低于设定温度0.1℃内。加热棒共计28根,加热功率分为3组2kW和1组8kW共计14kW,当温差较大时4组加热器同时工作,当快加热到设定温度时,仅3组2kW的加热棒工作。加热棒安装于浮箱底部并通过浮箱悬浮于水箱中(见图 6)。当水泵起动并进行标定实验时,整个标定装置内的水体会循环流动。通过合理布置水箱中进、出水管的位置,使得水箱中加热的水体充分掺混从而达到温度均匀。该标定装置的最大加热水温可达35℃。

|
| 图 6 加热浮箱照片 Fig.6 Photo of floating heater |
本次标定对象为西北工业大学微/纳米系统实验室研制的MEMS柔性热膜式壁面剪应力传感器,如图 7所示。该传感器的热敏元件长3mm,宽50μm,厚1μm,传感器的衬底为聚酰亚胺柔性薄膜,传感器的表面沉积有Parylene保护层。该传感器通过超薄聚酰亚胺胶带贴于安装盖板底部后,再将盖板固定于标定段上,如图 8所示。本次标定同时标定2个壁面剪应力传感器,传感器#1和#2在20℃时的阻值和电阻温度系数TCR分别为12.374Ω、3756ppm/℃和12.848Ω、3708ppm/℃。

|
| 图 7 MEMS柔性热膜式壁面剪应力传感器 Fig.7 MEMS flexible hot-film wall shear stress sensor |

|
| 图 8 安装于标定段的柔性热膜式壁面剪应力传感器 Fig.8 Wall shear stress sensor installed on the calibration section |
热膜式壁面剪应力传感器具有如下形式的标定公式[23]:
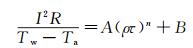 (5)
(5)
式中:I为传感器工作电流;R为热敏元件电阻;Tw为传感器工作温度;Ta为环境温度(即水温);ρ为流体介质密度;τ为壁面剪应力,系数n可取为1/3;A、B为需要通过标定实验来确定的标定系数。在某一温度的水体中,环境温度Ta和水的密度ρ均为常数。当热膜式壁面剪应力传感器工作在恒流驱动模式下时,传感器的工作电流I和工作温度Tw也为常数,根据欧姆定律,工作电压E = IR,式(5) 可简化为:
 (6)
(6)
标定实验时室温在10℃左右,水池中水体的温度分别设置在18.4、21、25和30℃,标定装置提供的最大剪应力在10Pa左右。因为水泵的发热和壁面剪应力做功等原因,标定过程中水温会缓慢上升,本次标定实验中水温上升最大只有0.3℃(对应18.4℃的组次),在30℃的水温下整个标定过程水温没有变化。由于对水体降温比较困难,做低温标定时可以在水箱内预先添加冰块或者在气温较低的时候进行标定。通过标定实验得到的拟合公式中各标定系数如表 1所示,拟合曲线如图 9和10所示。

|
| 图 9 编号1的壁面剪应力传感器在不同水温下的标定曲线 Fig.9 Calibration curves of #1 sensor at different water temperatures |

|
| 图 10 编号2的壁面剪应力传感器在不同水温下的标定曲线 Fig.10 Calibration curves of #2 sensor at different water temperatures |
从2个传感器的标定结果来看,标定公式对各温度下的剪应力与电压的关系均拟合良好,确定系数均大于0.90,不同温度下的标定曲线变化趋势均相似,但是各自的标定系数均不相同。2个传感器本身输出的电压范围也存在差异,这与各探头的基础阻值以及温度电阻系数不同有关。
需要指出的是在恒流驱动模式下工作的热膜式壁面剪应力传感器对环境温度十分敏感。2个传感器在水温18.4℃与30℃时的输出电压差值已经超出了同一温度下剪应力测量量程内的电压变化范围,因此在该仪器的应用中需要采用现场的水温进行标定。从标定系数来看,在标定水温的变化范围内,标定系数B随水温Ta呈线性变化的趋势,并且传感器#1和传感器#2的斜率相近,如图 11所示。该线性关系对应的温度范围在18.4~30℃,足以涵盖后续开展的河口海岸工程应用实验中的水温变化范围。在本次标定实验中,标定系数A与水温的关系并不明确,其具体关系还需要通过该装置进一步深入研究。

|
| 图 11 标定系数B与水温Ta的变化趋势 Fig.11 Variation trend of calibration coefficient B and water temperature Ta |
在恒流驱动模式下工作的热膜式壁面剪应力传感器在小剪应力范围内输出电压变化较大,因而在小剪应力的测量中更为灵敏,但在剪应力较大时容易出现输出饱和的现象,即曲线变得平缓,电压值分辨率降低。所以在应用实验时须提前估算剪应力的范围,进而选择适当规格的热膜式壁面剪应力传感器和工作电流来进行标定。
4 结论基于宽扁管道内壁面剪应力与沿程压力梯度的关系,研制了一种可温控的水下壁面剪应力传感器标定装置,并运用于MEMS柔性热膜式剪应力传感器在不同水温条件下的静态标定,得到了如下结论:
(1) 研制的可温控水下壁面剪应力传感器标定装置与标定方法可实现水下壁面剪应力传感器在不同水温条件下的静态标定。
(2) 标定实验表明恒流驱动模式下工作的热膜式壁面剪应力传感器受水温影响显著,不同基础阻值的热膜式壁面剪应力传感器的标定曲线变化趋势相似,但标定系数各不相同,标定系数B与水温呈线性相关。在水下应用实验中需用现场的水温进行标定。
(3) 恒流驱动模式下工作的热膜式壁面剪应力传感器对小剪应力反映灵敏,当剪应力较大时会出现输出饱和的现象,在水下应用实验前需要选择适当的传感器和工作模式进行标定。
致谢: 西北工业大学微/纳米系统实验室马炳和教授的团队为本文的标定实验提供了MEMS柔性热膜式剪应力传感器和帮助,作者在此感谢。| [1] | Xu H, Xia Y F, Ma B H, et al. Research on measurement of bed shear stress under wave-current interaction[J]. China Ocean Engineering, 2015, 29: 589–598. DOI:10.1007/s13344-015-0041-z |
| [2] | 吕海峰, 姜澄宇, 邓进军, 等. 用于壁面切应力测量的微传感器设计[J]. 机械工程学报, 2010, 46(24): 54–60. Lyu H F, Jiang C Y, Deng J J, et al. Design of micro sensor for wall shear stress measurement[J]. Journal of Mechanical Engineering, 2010, 46(24): 54–60. |
| [3] | Ma B H, Ma C Y. A MEMS surface fence for wall shear stress measurement with high sensitivity[J]. Microsystem Technologies, 2016, 22(2): 239–246. DOI:10.1007/s00542-015-2450-6 |
| [4] | Savelsberg R, Schiffer M, Obermeier E, et al. Calibration and use of a MEMS surface fence for wall shear stress measurements in turbulent flows[J]. Experiments in Fluids, 2012, 53(2): 489–498. DOI:10.1007/s00348-012-1304-6 |
| [5] | 马炳和, 赵建国, 邓进军, 等. 全柔性热膜微传感器阵列制造工艺及性能优化[J]. 光学精密工程, 2009, 17(8): 1971–1977. Ma B H, Zhao J G, Deng J J, et al. Fabrication of flexible hot film sensor array and its optimization[J]. Optics and Precision Engineering, 2009, 17(8): 1971–1977. |
| [6] | Miau J J, Leu T S, Yu J M, et al. MEMS thermal film sensors for unsteady flow measurement[J]. Sensors and Actuators A: Physical, 2015, 235: 1–13. DOI:10.1016/j.sna.2015.09.030 |
| [7] | Pujara N, Liu P L F. Direct measurements of local bed shear stress in the presence of pressure gradients[J]. Experiments in Fluids, 2014, 55(7): 1–13. |
| [8] | Huo G, Wang Y G, Yin B S, et al. A new measure for direct measurement of the bed shear stress of wave boundary layer in wave flume[J]. Journal of Hydrodynamics, Ser B, 2007, 19(4): 517–524. DOI:10.1016/S1001-6058(07)60148-6 |
| [9] | Hultmark M, Smits A J. Temperature corrections for constant temperature and constant current hot-wire anemometers[J]. Measurement Science and Technology, 2010, 21(10): 105404. DOI:10.1088/0957-0233/21/10/105404 |
| [10] | Talluru K M, Kulandaivelu V, Hutchins N, et al. A calibration technique to correct sensor drift issues in hot-wire anemometry[J]. Measurement Science and Technology, 2014, 25(10): 105304. DOI:10.1088/0957-0233/25/10/105304 |
| [11] | 马炳和, 王毅, 姜澄宇, 等. 柔性热膜剪应力传感器水下测量温度修正[J]. 实验流体力学, 2014, 28(2): 39–44. Ma B H, Wang Y, Jiang C Y, et al. Temperature correction of flexible thermal shear stress sensor for underwater measurements[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 39–44. DOI:10.11729/syltlx20140006 |
| [12] | Sumer B M, Arnskov M M, Christiansen N, et al. Two-component hot-film probe for measurements of wall shear stress[J]. Experiments in Fluids, 1993, 15(6): 380–384. DOI:10.1007/BF00191776 |
| [13] | Xu Y, Lin Q, Lin G Y, et al. Micromachined thermal shear-stress sensor for underwater applications[J]. Journal of Microelectromechanical Systems, 2005, 14(5): 1023–1030. DOI:10.1109/JMEMS.2005.856644 |
| [14] | 田于逵, 谢华, 黄欢, 等. MEMS壁面剪应力传感器阵列水下标定实验研究[J]. 实验流体力学, 2015, 29(2): 8–12. Tian Y K, Xie H, Huang H, et al. Calibration of MEMS wall shear-stress-sensor array for underwater applications[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(2): 8–12. |
| [15] | 徐华. 波流作用下床面切应力及挟沙能力研究[D]. 南京: 河海大学, 2016. Xu H. Research on bed shear stress and sediment-carrying capacity under wave-current interaction[D]. Najing: Hohai University, 2016. |
| [16] | Pope S B. Turbulent flows[M]. New York: Cambridge University Press, 2001: 802. |
| [17] | Marusic I, Mckeon B J, Monkewitz P A, et al. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues[J]. Physics of Fluids, 2010, 22(6): 065103.1–24. DOI:10.1063/1.3453711 |
| [18] | Vinuesa R, Schlatter P, Nagib H M. On minimum aspect ratio for duct flow facilities and the role of side walls in generating secondary flows[J]. Journal of Turbulence, 2015, 16(6): 588–606. DOI:10.1080/14685248.2014.996716 |
| [19] | Knight D W, Patel H S. Boundary shear in smooth rectangular ducts[J]. Journal of Hydraulic Engineering, 1985, 111(1): 29–47. DOI:10.1061/(ASCE)0733-9429(1985)111:1(29) |
| [20] | Rhodes D G, Knight D W. Distribution of shear force on boundary of smooth rectangular duct[J]. Journal of Hydraulic Engineering, 1994, 120(7): 787–807. DOI:10.1061/(ASCE)0733-9429(1994)120:7(787) |
| [21] | Monty J P. Developments in smooth wall turbulent duct flows[D]. Melbourne: University of Melbourne, 2005. |
| [22] | Vinuesa R, Bartrons E, Chiu D, et al. New insight into flow development and two dimensionality of turbulent channel flows[J]. Experiments in Fluids, 2014, 55(6): 1–14. |
| [23] | Hanratty T J, Campbell J A. Measurement of wall shear stress[M]//Fluid Mechanics Measurements. Washington D C: Taylor & Francis, 1996: 575-648. |