流体壁面剪应力测量对于流动减阻、湍流结构机理研究等方面都具有重要作用,但是这一物理量较难测得。近年来,MEMS技术的发展推动了传感器尺寸的微小化,MEMS传感器为壁面剪应力的测量提供了一种准确有效的手段。国内外许多研究机构已经开展了各类MEMS壁面剪应力传感器的设计制造。为了关联壁面剪应力和输出信号,评估传感器的工作性能指标,许多研发单位开展了传感器的标定研究工作,但是至今为止尚未有统一的标定方法形成。
Xu Yong[1]等人使用微型扁平水槽对水下MEMS剪应力传感器进行了标定。尽管该方法能够产生稳定可靠的壁面剪应力,但剪应力量级较小。另外,层流底层速度剖面是线性的,而二维泊肃叶流动的主流速度剖面为抛物线,因此该壁面剪应力公式不适用于层流底层。Allan J.Zuckerwar[2]和Khoo B. C.[4]对旋转流道标定方法进行了研究,并就轮子的直径、宽度和安装传感器的位置对标定的影响进行了一系列的公式修正。旋转流道法的标定量程大,但是它只适用于层流标定。L.Löfdahl[5]采用平板试验方法完成了对MEMS热传感器的标定,其使用多项式拟合和修正的King公式2种方法对输出电压和输入剪应力建立了函数关系。国内的项志杰等人[6]也采用平板流动法标定了MEMS传感器。平板方法适用于层流和湍流标定,传感器安装方便,但是粘性底层速度剖面测量具有难度,使用外推法获得的壁面剪应力存在一定的误差。Aravind Padmanabhan等人[7-8]和田于逵等人[9-11]均采用压力梯度法进行了标定研究。压力梯度法的试验装置为扁平槽道,在扁平槽道中不论流动状态是层流还是湍流,压力梯度与壁面剪应力的关系都能成立,且产生壁面剪应力的数值范围较大,因此较多地用于壁面剪应力传感器的标定。
本文针对恒流驱动式热膜型MEMS壁面剪应力传感器进行水中标定及不确定度分析。标定采用压力梯度法,使用扁平校验水槽作为主要的试验装置。通过各个工况下输入壁面剪应力与输出电压的采集与分析获得了传感器的标定曲线,通过系统分析及重复多次测量分析输入及输出信号的不确定度,从而判断MEMS传感器性能的可靠性及壁面剪应力信号的准确性。
1 试验设备和测量仪器标定试验在扁平校验水槽完成,试验段为长×宽×高=2350mm×250mm×20mm的扁平槽道,流速范围为0~5m/s,湍流度小于1%,流场品质优良。扁平水槽的高度远小于水槽宽度和长度,且流场均匀,符合压力梯度法的理论模型。
本文标定对象为热膜型MEMS壁面剪应力传感器阵列,阵列尺寸长×宽×厚=70mm×50mm×0.075mm,包含8个敏感单元,各单元尺寸长×宽=3mm×0.55mm,间距6.3mm,如图 1所示。

|
| 图 1 MEMS壁面剪应力传感器阵列示意图 Fig.1 MEMS wall shear stress sensor array diagram |
热膜型MEMS壁面剪应力传感器采用恒流驱动模式,在恒流模式下,传感器内的电流保持恒定,流动带走热量使得热敏电阻两端电压发生变化,壁面剪应力的大小可通过电压值来判断。本文对图 1中2、5、6和7这4个敏感单元进行标定和应用检验研究(由于制造和安装过程中的磕碰,最后能够正常工作的只有编号为2、5、6和7的4个单元),在20℃下,这4个单元的电气参数分别如表 1所示。
MEMS传感器及信号带用可去除胶粘贴于盖板内侧,信号带通过矩形通孔引出,对引线孔作水密处理,如图 2所示。

|
| 图 2 MEMS传感器安装示意图 Fig.2 MEMS sensor installation instruction |
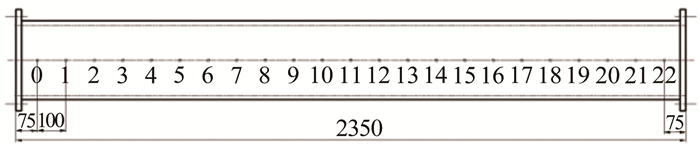
盖板布置在距离试验段前缘1675mm处,如图 3所示。测压孔分布情况如图 4所示。

|
| 图 3 盖板布置图 Fig.3 Diagram of coverplate |
|
| 图 4 测压孔分布图 Fig.4 Diagram of pressure taps |
根据Bellhouse的公式[3],焦耳加热的二维线性层流热边界层可以表示为:
 (1)
(1)
由于强制对流热传输假设受制于传感器的有效长度,同时热边界层也不可能完全是线性的,因此在实际的湍流流动,将Bellhouse公式修正为:
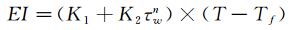 (2)
(2)
若已知热敏元件的电阻温度系数α,温度Tref下的电阻值Rref,则在温度T时,热敏元件的电阻值R为:
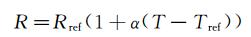 (3)
(3)
当输入壁面剪应力为0时,热敏元件的电阻值为:
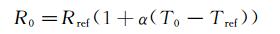 (4)
(4)
由公式(1) 和(2) 可得:
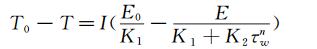 (5)
(5)
由公式(3) 和(4) 可得:
 (6)
(6)
传感器采用恒流供电方式工作,则由公式(5) 和(6) 可得:
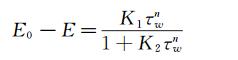 (7)
(7)
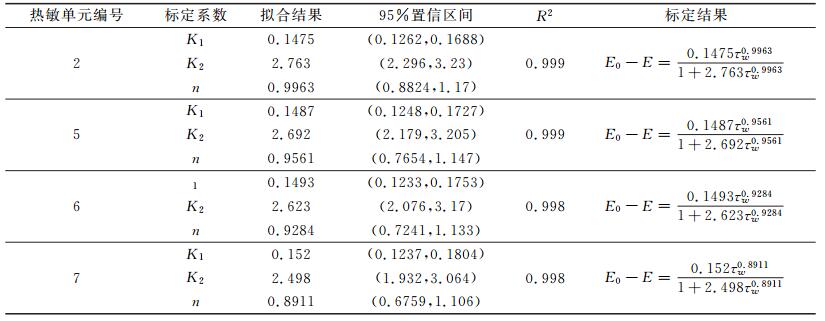
E、E0和τw均为试验测得,K1、K2和n为标定系数,在相同温度下为常值,通过最小二乘法可以获得标定系数的数值[12]。
3 实验结果及其不确定度分析标定需建立输入壁面剪应力和输出电压之间的关系:
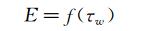 (8)
(8)
壁面剪应力的计算公式为:
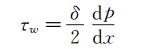 (9)
(9)
根据标定和不确定度分析的要求,需要对标定装置扁平试验段高度、压力梯度和输出电压进行独立重复测量[13-14]。
3.1 电压的测量结果及其不确定度分析MEMS传感器的输出电压由24位NI数据采集卡直接进行采集。在相同温度下进行8次独立重复测量。
E0-E的不确定度分析数学模型为:ΔE=E0-E,以多次测量的平均值作为测量结果。ΔE的不确定度来源于E0和E的不确定度,而E0和E的不确定度来源于:(1) A类标准不确定度,可由多次重复测量评定。一般情况下,当独立重复测量次数n≥6时,GJB3756-99推荐使用贝塞法计算实验标准偏差s(x)。单次测量值作为测量结果时,由重复性引入的测量不确定度uA=s(x),算术平均值作为测量结果时A类标准不确定度的计算公式为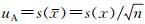
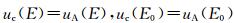
E0和E的测量相互独立,由不确定度合成法则可知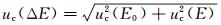

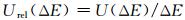
根据壁面剪应力的计算公式(9) 可知,壁面剪应力的测量不确定度来源于试验段槽道高度δ及dp/dx的测量不确定度,因此可分4步来求取τw的不确定度:(1) 计算压力测量结果p的合成标准不确定度uc(p);(2) 求dp/dx的合成标准不确定度uc(dp/dx);(3) 计算δ的合成标准不确定度uc(δ);(4) 获得τw合成标准不确定度uc(τw)及其扩展不确定度U(τw)。
(1) 压力测量结果p的合成标准不确定度uc(p)
压力信号的获取过程如下:压力信号-压力变送器-信号转换器-数据采集系统,因此压力测量结果p的标准不确定度来源于:(1) A类标准不确定度uA(p);(2) 压力传感器引入的B类标准不确定度uB1(p),该压力传感器的测量精度为0.1%;(3) 信号转换器引入的B类标准不确定度uB2(p),其测量精度为0.5%;(4) 数据采集系统引入的B类标准不确定度uB3(p),其设备等级为0.5级。则压力测量结果p的合成标准不确定度为uc(p)= 
(2) dp/dx的合成标准不确定度uc(dp/dx)
uc(dp/dx)的不确定度来源于:(1) 压力p的测量不确定度传递给dp/dx的不确定度uc1(dp/dx);(2) 最小二乘法线性拟合引入的不确定度uc2(dp/dx)。
已知试验数据x1,x2,…xn和y1,y2,…yn,使用最小二乘法进行过原点线性拟合,即要求直线y=bx使得残差平方和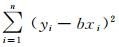
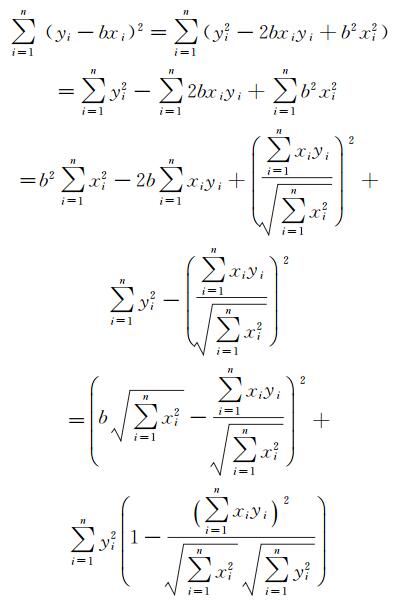 (10)
(10)
显然,当且仅当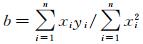
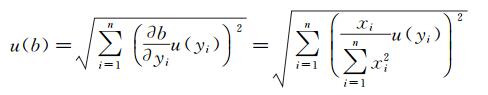 (11)
(11)
对压力测量结果p和位置参数x进行线性拟合,其斜率dp/dx可通过最小二乘法获得,则uc1(dp/dx)的计算可基于公式(10) 和(11)。则根据上述分析,若已知压力在各个测点处的测量不确定度uc(pi)(i=1, 2…,22),则由uc(pi)引起的dp/dx的不确定度可表示为:
 (12)
(12)
由于测压孔的制造安装等造成的随机误差,压力测量值会偏离拟合线。uc2(dp/dx)用于表征该类随机影响因素造成的不确定度。线性模型的矩阵形式可以写成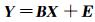

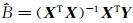

由上述分析可知,对于过原点最小二乘线性拟合,系数矩阵仅含拟合线斜率b,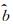
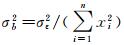
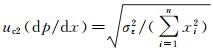
由不确定度合成法则可知,压力梯度的合成标准不确定度为:
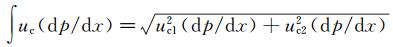 (13)
(13)
(3) δ的合成标准不确定度uc(δ)
取多次测量的平均值作为水槽高度δ的测量结果,其不确定度来源于:(1) A类标准不确定度;(2) 游标卡尺示值误差引入的B类标准不确定度;(3) 游标卡尺分辨力引入的B类标准不确定度。δ的合成标准不确定度为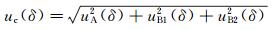
扁平试验段高度δ与沿程压力梯度dp/dx的测量值彼此独立不相关,则根据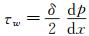
 (14)
(14)
在0.95置信概率下,包含因子k=2,即壁面剪应力的扩展不确定度为U(τw)=2uc(τw),具体计算结果如表 2所示。从表中可以发现,流速越高壁面剪应力的测量不确定度越小,校验水槽在高流速下具有较高的流场品质。
将壁面剪应力数据作为输入信号,电压测量数据作为输出信号,通过标定公式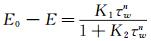
设置偏差函数
在曲线拟合中R2为拟合值和试验值之间相关系数的平方,在所有测量数据等权情况下R2的计算公式为: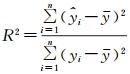
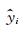
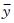
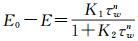

|
| 图 5 2号热敏单元标定曲线 Fig.5 Calibration curve of No.2 sensor element |
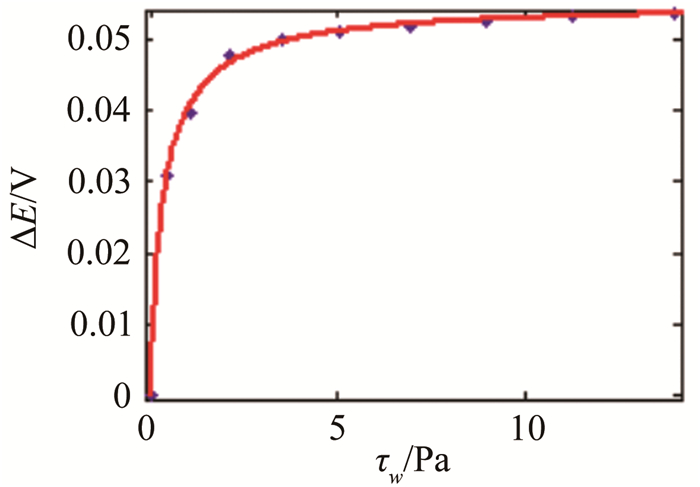
|
| 图 6 5号热敏单元标定曲线 Fig.6 Calibration curve of No.5 sensor element |
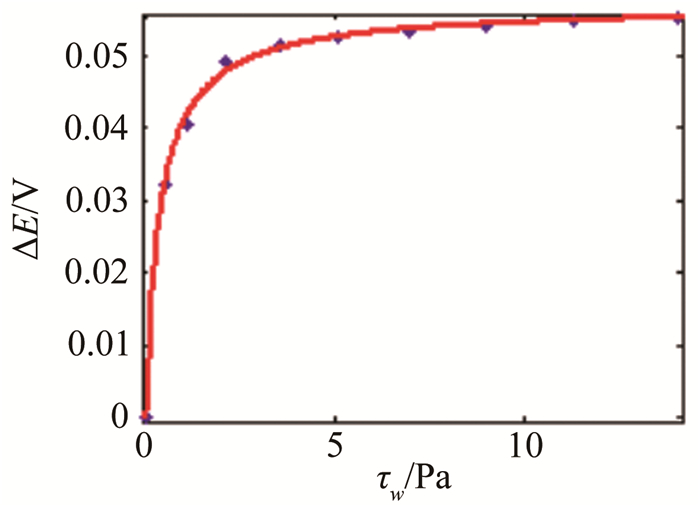
|
| 图 7 6号热敏单元标定曲线 Fig.7 Calibration curve of No.6 sensor element |
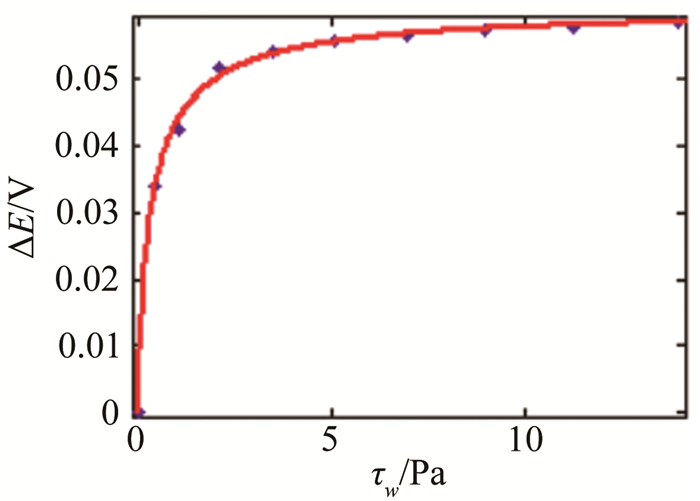
|
| 图 8 7号热敏单元标定曲线 Fig.8 Calibration curve of No.7 sensor element |
针对热膜型MEMS壁面剪应力传感器进行了标定分析工作。标定采用压力梯度法,使用扁平校验水槽作为主要的试验装置。通过各个工况下壁面剪应力信号与输出电压信号的采集与分析获得了传感器的标定曲线;通过重复多次测量数据分析了壁面剪应力测量的不确定度以及电压信号测量的不确定度。
试验结果表明,剪应力测量的相对扩展不确定度小于7%,且外流速度越大,剪应力测量的不确定度越小,因此扁平校验水槽能够提供较高精度的剪应力输入;电压测量的相对扩展不确定度小于7%,且外流速度越大,电压测量的不确定度越小,因此传感器能够可靠地用于流体壁面剪应力的测量;标定系数曲线的相关系数较大,因此标定公式具有较高的可靠性。
| [1] | Xu Y, Lin Q, Lin G, et al. Micromachined thermal shear-stress sensor for underwater applications[J]. Microelectromechanical Systems, 2005, 14(5): 1023–1030. DOI:10.1109/JMEMS.2005.856644 |
| [2] | Zuckerwar A, Michael A S. A rotary flow channel for shear stress sensor calibration[C]//24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, 28 June-1 July, 2004. |
| [3] | Bellhouse B J, Schultz D L. Determination of mean and dynamic skin friction, separation and transition in low-speed flow with a thin-film heated element[J]. Journal of Fluid Mechanics, 1966, 24: 379–400. DOI:10.1017/S0022112066000715 |
| [4] | Khoo B C, Chew Y T, Lim C P, et al. The flow between a rotating and a stationary disc: application to near-wall hot-wire calibration[J]. Measurement Science & Technology, 1998, 9(4): 650–658. |
| [5] | Löfdahl L, Chernoray V, Haasl S, et al. Characteristics of a hot-wire microsensor for time-dependent wall shear stress measurements[J]. Experiments in Fluids, 2003, 35(3): 240–251. DOI:10.1007/s00348-003-0624-y |
| [6] | 项志杰, 马炳和, 邓进军, 等. 浮动式剪应力微传感器的标定[J]. 微纳电子技术, 2014(4): 236–242. Xiang Z J, Ma B H, Deng J J, et al. Calibration of floating-element micro wall shear stress sensor[J]. Micro-nano-electronic Technology, 2014(4): 236–242. |
| [7] | Padmanabhan A. Silicon micromachined sensors and sensor arrays for shear-stress measurements in aerodynamic flows[R]. Aerospace Computational Design Laboratory, Dept of Aeronautics & Astronautics, Massachusetts Institute of Technology, 1997. |
| [8] | De Luca A, Haneef I, Coull J, et al. High sensitivity single thermopile SOI CMOS MEMS thermal wall shear stress sensor[J]. IEEE Xplore, 2015: 1. |
| [9] | 黄欢, 孙海浪, 田于逵, 等. 水下MEMS剪应力标定试验压力监测方案设计[C]. 全国水动力学学术会议暨全国水动力学研讨会, 青岛: 2014. Huang H, Sun H L, Tian Y K, et al. Pressure monitor project design of under water MEMS shear stress cabibration test[C]. Proceedings of National Congress on Hydrodynamics & National Conference on Hydrodynamics, Qingdao: 2014. |
| [10] | 田于逵, 谢华, 黄欢, 等. MEMS壁面剪应力传感器阵列水下标定实验研究[J]. 实验流体力学, 2015, 29(2): 8–12, 25. Tian Y K, Xie H, Huang H, et al. Calibration research of MEMS shear stress sensor array[J]. Experimental Fluid Mechanics, 2015, 29(2): 8–12, 25. |
| [11] | Tian Y K, Xie H, Huang H, et al. Calibration of MEMS wall shear-stress-sensors array for underwater applications[J]. Journal of Experiments in Fluid Mechanics, 2015: 8–12. |
| [12] | 李晓莹, 李雁冰, 马炳和, 等. 微型热膜传感器的水下壁面剪应力标定研究[J]. 传感器与微系统, 2014, 33(10): 11–13. Li X Y, Li Y B, Ma B H, et al. Under water wall shear stress calibration reserch of micro thermal sensor[J]. Transducer and Microsystem Technologies, 2014, 33(10): 11–13. |
| [13] | 国家质量监督检验检疫总局. JJF1059-1999测量不确定度评定与表示[S]. 北京: 中国计量出版社, 1999. JJF1059-1999. Evaluation and expression of measurement uncertainties[S]. Beijing: State Administration for Quality Supervision and Inspection and Quarantine, 1999. http://d.wanfangdata.com.cn/Periodical_gyjl200602015.aspx |
| [14] | 钱绍圣. 测量不确定度[M]. 北京: 清华大学出版社, 2002. Qian S S. Measurement uncertainty[M]. Beijing: Tinghua University Press, 2002. |
| [15] | 林洪桦. 测量误差与不确定度评估[M]. 北京: 机械工业出版社, 2010. Lin H Y. Measurement error and uncertainty evaluation[M]. Beijing: China Machine Press, 2010. |
| [16] | 范影乐. MATLAB仿真应用详解[M]. 北京: 人民邮电出版社, 2001. Fan Y L. MATLAB simulation and application examples[M]. Beijing: Posts and Telecom Press, 2001. |