2. 河海大学 港口海岸与近海工程学院, 南京 210098;
3. 水文水资源与水利工程科学国家重点实验室, 南京 210098;
4. 港口航道泥沙工程交通行业重点实验室, 南京 210024
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. The State Key Laboratory of Hydrology-water Resources and Hydraulic Engineering, Nanjing 210098, China;
4. Key Laboratory of Port, Waterway and Sedimentation Engineering of Ministry of Transport, Nanjing 210024, China
在河口海岸工程基础理论与工程应用中,泥沙起动、推移质输沙以及悬沙底部参考点浓度的估算都离不开床面剪应力。波浪由深海传播到近岸时,波浪开始触底,受水深减小以及底部摩阻的影响,波浪会发生变形直到破碎[1]。破波区是泥沙输运以及地貌演变最活跃的区域,波浪破碎属于复杂的强非线性运动,会带来强烈的紊动和涡旋。研究波浪破碎对床面剪应力的影响对于揭示破波区泥沙输运具有重要意义。
由于波浪边界层内的床面剪应力具有量级小、正负交替和变化快等特点,直接而准确地测量其底部剪应力仍具有挑战性。常用的波浪床面剪应力直接测量仪器为应力板[2-3],通过应力板的位移或者直接测量作用于底板上的力来获得床面剪应力。在波浪作用下,应力板的前沿和后沿之间会存在一个压力梯度,Pujara等[4-5]研制了一种考虑了边缘压力梯度影响的应力板, 并应用于孤立波冲流运动的研究中。除了压力梯度的问题,应力板测得床面剪应力实质上是作用于应力板表面的平均应力,因此其测量的空间分辨率会受到影响。另一种常用的直接测量仪器是嵌平式热膜探针[6-7]。热膜探针较传统的应力板具有高响应度的优势,并且不存在压力梯度的问题,因此常用于波浪边界层的研究[8-9]之中。
目前,还出现了其他一些新型测量仪器用于波浪边界层内的床面剪应力测量。Musumeci等[10]采用磁流体微刺的位移来测量波浪底部剪应力。随着微机电系统(MEMS)技术的发展,MEMS柔性热膜式壁面剪应力传感器也为波浪边界层内的床面剪应力测量提供了新的手段。梁婷等[11]验证了该传感器在波浪作用下床面剪应力测量中的可行性,Xu等[12]则采用该传感器研究了波流相互作用下床面剪应力情况。
有关破碎波作用下的床面剪应力直接测量的报道较少。Boers[13]采用应力板测量了带沙坝地形上的破波区床面剪应力,Deiggard等[14]、Yüksel等[15]和Sumer等[16-17]均采用嵌平式热膜探针对破碎波下的床面剪应力进行了研究。嵌平式热膜探针进行安装时可能会存在边壁对齐问题,加上探针尺寸较小,会给测量的准确性带来影响。与MEMS柔性热膜式壁面剪应力传感器相比,该探针安装于弯曲表面时会存在接缝处间断的问题。另外一种间接测量的方法是测量波浪边界层内的流速分布,进而计算得到床面剪应力的大小。当波浪破碎剧烈时,破碎波产生的紊动和涡旋可能会侵入到波浪边界层内,在这种情形下使用间接测量方法会存在一定的不确定性。
本文延续Xu等[12]的工作,采用新型的MEMS热膜式壁面剪应力传感器对破碎波作用下的床面剪应力进行了应用测试。根据实验结果讨论了该传感器在破碎波作用下的工作情况,并初步探明了破碎波作用下床面剪应力的变化规律。
1 柔性热膜式壁面剪应力传感器实验所用的壁面剪应力传感器为西北工业大学微/纳米系统实验室研制的MEMS柔性热膜式壁面剪应力传感器,如图 1所示。该传感器的热敏元件长3mm,宽50μm,厚1μm。传感器的衬底为聚酰亚胺柔性薄膜,传感器表面沉积有Parylene保护层。

|
| 图 1 MEMS柔性热膜式壁面剪应力传感器 Fig.1 MEMS flexible hot-film wall shear stress sensor |
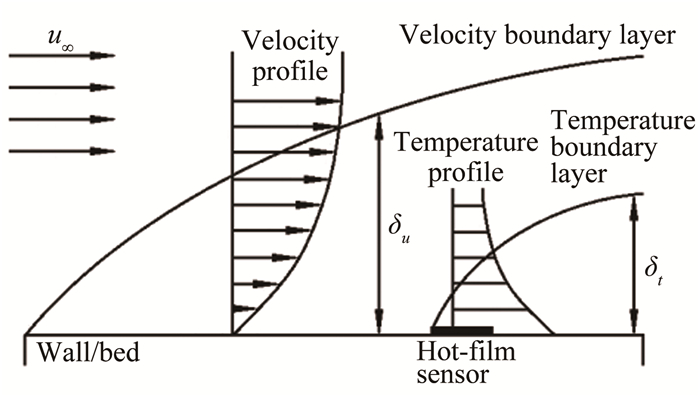
该剪应力传感器的水下工作原理如图 2所示。传感器的热敏元件通过一定电流后产生热量,当热敏元件表面的流体流动时会发生强迫对流换热从而带走热量。元件本身具有热敏电阻特性,通过电桥检测热敏元件电阻的变化可获得元件温度的变化,再根据热平衡关系和强迫对流换热关系可以得到流速以及与流速相关的流量、壁面剪应力等信息。普朗特数Pr是流体固有的物性参数,反映了速度边界层厚度δu和温度边界层厚度δt之间关系。室温下液态水的Pr>1,其速度边界层厚于温度边界层[18],热敏元件的热平衡变化仅反映速度边界层内的信息,因此热膜式剪应力传感器可以用于测量水下壁面剪应力。
|
| 图 2 柔性热膜式壁面剪应力传感器工作原理 Fig.2 Operating principle of flexible hot-film shear stress sensor |
热敏元件电阻的变化通过电压信号变化反映。根据对热敏元件加热的方式不同,该传感器的驱动模式分为恒流、恒压和恒温式。本文采用的驱动模式为恒流式驱动。该热膜式剪应力传感器在测试应用前需进行标定,以建立传感器输出电压E与壁面剪应力τb的标定关系。热膜式壁面剪应力传感器对环境温度的变化敏感[19],对恒流驱动模式下工作的传感器还没有很好的水下温度校正方法,因此需要对现场不同的水温条件进行标定。
破碎波实验所用的传感器由具有温控功能的水下壁面剪应力传感器标定装置标定,该装置可实现不同水温条件下的传感器标定。该装置的标定段为矩形截面的宽扁管道,管道长3000mm、宽220mm、高20mm。考虑到管道边壁的影响,标定段内壁面剪应力与沿程压力梯度的关系可由下式计算[20]:
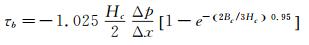 (1)
(1)
式中:τb为上下壁面中心线上的最大剪应力;Bc为宽扁管道的宽度;Hc为宽扁管道的高度。
恒流驱动膜式下的MEMS柔性热膜式壁面剪应力传感器具有如下形式的标定公式[12]:
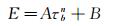 (2)
(2)
式中:A、B、n为需要通过标定实验来确定的标定系数。本次应用研究即采用标定公式换算测量的底部剪应力。在破碎波实验前,需根据波浪水槽内的水体温度对实验所用的传感器分别进行标定。如果水温变化过大,则需要在波浪实验之后进行补充标定。
2 破碎波实验布置破碎波实验在南京水利科学研究院的波浪水槽中进行,波浪水槽工作段长40m,宽0.8m,深1m(见图 3)。水槽头部配有具有主动吸收功能的推板式造波机,可产生各种波浪要素的规则波和不规则波。实验中的波高由南京水利科学研究院研制的NH型电导式波高仪测量,采样频率为50Hz。水槽侧壁安装有高清摄像机,用以记录波浪破碎过程。流速由Nortek Vectrino三维声学多普勒点式流速仪(ADV)测量,流速测点距探头5cm,采样频率25Hz。流速测量主要用于辅助判别剪应力的方向,ADV的流速测点距离传感器上方5mm处,采样点高度为4.6mm。

|
| 图 3 波浪实验水槽 Fig.3 Wave flume used for the test |
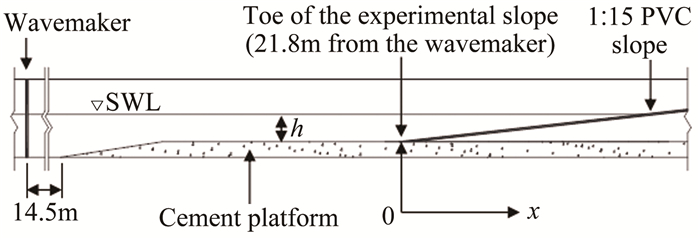
波浪水槽的实验布置如图 4所示。斜坡的坡度为1:15,斜坡坡脚距离造波机21.8m。实验斜坡采用厚度为8mm的光面PVC塑料板拼接而成,接缝处用玻璃胶密封,玻璃胶用小刀刮平以后表面再用厚度为0.05mm的PET聚酯薄膜胶带覆盖以保证接缝处平整光滑。实验斜坡底部采用桁架支撑,并用螺栓固定于波浪水槽底部的水泥平台上。实验斜坡与波浪水槽侧壁的接缝处用玻璃胶密封。
|
| 图 4 波浪水槽实验布置图 Fig.4 Setup of the experimental wave flume |
斜坡上每间隔一段距离安装剪应力传感器。剪应力传感器连同标定时使用的有机玻璃底板一起安装于斜坡上(见图 5)。剪应力传感器与斜坡接缝处用工业橡皮泥填充密封后再用小刀刮平。剪应力传感器在实验斜坡上的布置位置如表 1所示。剪应力传感器的采样频率为500Hz,采样时间为60s。实验过程中波浪水槽内水温范围为21~21.5℃。

|
| 图 5 安装于实验斜坡上的剪应力传感器 Fig.5 Wall shear stress sensor installed on the experimental slope |
测试应用实验采用的入射波浪为规则波,波浪的破碎形式可由破波相似系数区分,当以深水的波浪要素表示时,破波相似系数ξ0定义如下:
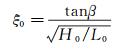 (3)
(3)
式中:tanβ为实验斜坡的坡度;H0为深水波高;L0为深水波长。当ξ0 < 0.5时为崩破波;当0.5 < ξ0 < 3.3时为卷破波;当3.3 < ξ0为激破波。当忽略波浪在浅化过程中的能量损失时,根据波能流守恒和线性波理论,深水波高H0可由下式计算:
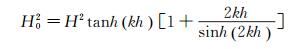 (4)
(4)
式中:H为斜坡坡脚处的波高;h为斜坡坡脚处的水深;波数k=2π/L;L为斜坡坡脚处的波长。其中k可根据波浪色散关系公式,由波浪周期T和h计算得到。
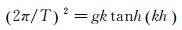 (5)
(5)
式中:g为重力加速度。深水波长L0 = gT2/(2π)。
本次破碎波测试应用采用的波浪要素汇总于表 2。波浪水槽中实际观测到的波浪破碎形式为卷破波,与根据深水破波相似参数ξ0区分的相一致。
由于该剪应力传感器无法识别方向,因此需要通过ADV测量的流速辅助判断方向。方向判断的依据主要有2点:一是波浪边界层内的床面剪应力与主流存在小于45°的相位超前[9],并且在越接近床面的地方相位差越小;二是根据近底流速在向岸和离岸方向的极值大小以及持续时间来判断。
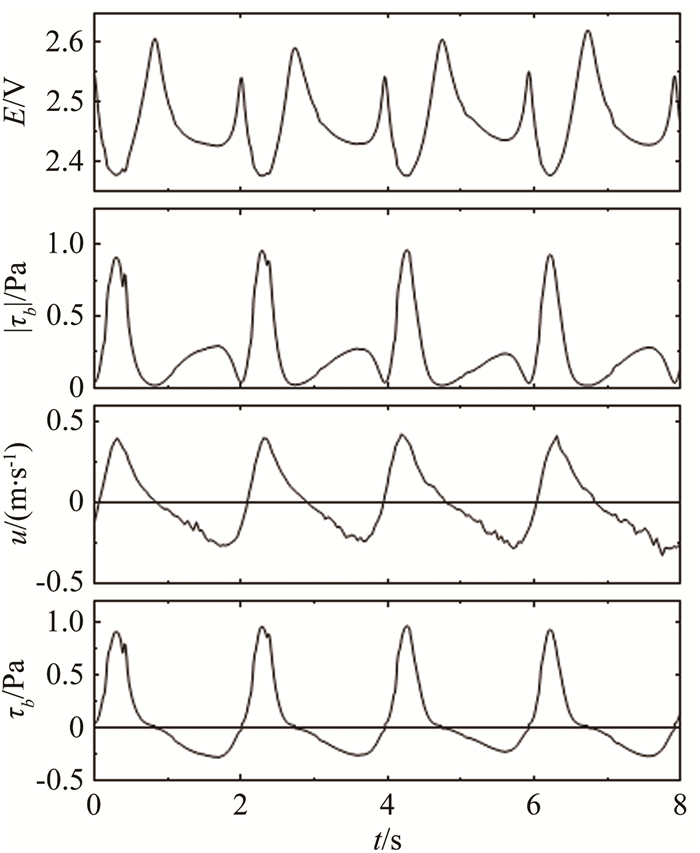
图 6为测量断面H2处床面剪应力与流速对比图。传感器可以直接测量出床面剪应力的连续变化情况。在规则波作用情况下,传感器输出电压也呈现周期性变化。在一个周期内(2s),输出电压会出现2个峰值和2个谷值,分别对应的是床面剪应力发生转向和达到最大值的位置。图中第2行为标定公式计算得到的床面剪应力|τb|。标定公式为幂函数的形式,因此计算得到最小床面剪应力只会趋近于0。图中第4行为根据同步测量的近底流速u进行方向判断以后得到的床面剪应力τb, 正值表示向岸方向,负值表示离岸方向。
|
| 图 6 测量断面H2处床面剪应力与流速对比图 Fig.6 Bed shear stress and measured velocity at Section H2 |
需要指出的是ADV在近壁处的流速测量上还存在一定的不确定性。Koca等[21]认为测点距离床面1.7~5mm高度的范围内会受到床面的干扰,其影响程度取决于床面的材料特性。本研究中ADV的流速采样点高度为4.6mm,接近于流速测点距剪应力传感器的距离,但从实验结果来看,剪应力传感器上方5mm处同步测量的流速可以用于在波浪未破碎情况下的床面剪应力方向判断。
在波浪剧烈破碎的地方存在很强的掺气现象(见图 7),此时ADV和剪应力传感器的信号都会受到气泡的干扰。波浪破碎以后带来的紊动和涡旋也会对方向的判断带来不确定性。在ADV信号被干扰的测量断面,只记录床面剪应力的绝对值|τb|。

|
| 图 7 H5断面波浪破碎过程 Fig.7 Snapshot of breaking process at Section H5 |
大部分水下测量仪器都会受掺气的影响,例如ADV、LDV(激光多普勒流速仪)等,这里掺气现象会对传感器的输出和壁面剪应力的大小同时产生一定的影响。空气的换热效率较水要低,当气泡经过传感器时,热敏元件的温度会突然升高,该传感器的输出电压也会升高,与没有气泡的情形相比,此时会短暂地输出一个较小的壁面剪应力。这与实际情形也是相对应的,因为掺气会使壁面剪应力减小[22]。由于标定公式是在水下情况得到的,空气产生的壁面剪应力虽然较相同情况下的水介质要小,但减小的具体大小并不能通过水下标定公式得到。对于河口海岸泥沙问题的研究,一般只关心床面剪应力极大值的大小,并且根据视频记录,本次实验中气泡主要集中于水体上部,少部分触底的气泡也很快会因为浮力而脱离床面。因此,结合该传感器的工作原理和应用目标,掺气现象不影响对床面剪应力极大值的研究。
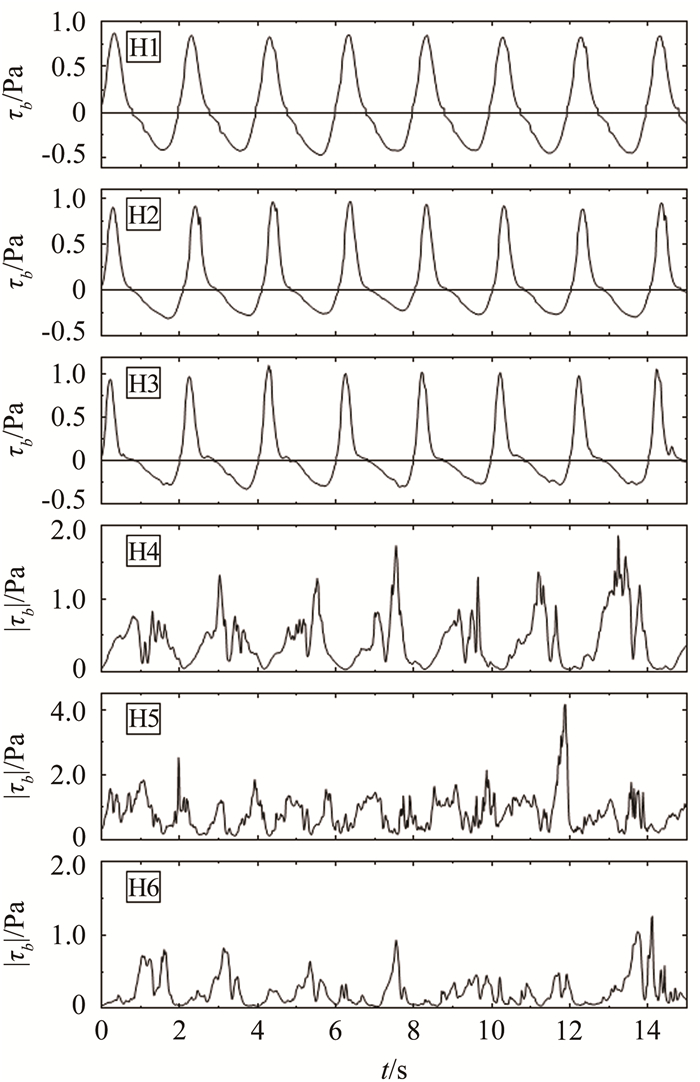
图 8为斜坡上沿程各测量断面的床面剪应力随时间变化的情况。其中断面H4~H6由于前面提到的方向判别问题,只给出床面剪应力的绝对值。波浪在破碎前(见图 8中断面H1~H3),床面剪应力呈周期性变化,向岸方向的最大床面剪应力大于离岸方向的最大剪应力,但是床面剪应力在向岸方向的持续时间要比离岸方向短。这与波浪在斜坡上浅化时波浪形状变为不对称有关。此时,床面剪应力仍由波浪边界层主导。当波浪破碎以后(见图 8中断面H4~H6),床面剪应力信号的变化在破碎以后仍然呈现一定的周期性变化,但部分周期存在一定的偏移。这是波浪在破碎以后产生的强非线性积累的结果。波浪破碎产生的紊动和涡旋侵入到波浪边界层,对床面剪应力的信号产生显著的影响,与波浪破碎前相比,床面剪应力的波动变得剧烈。
|
| 图 8 斜坡沿程各断面的床面剪应力时间序列 Fig.8 Time series of bed shear stress along the slope |
各测量断面的最大床面剪应力均值|τm|通过下式计算:
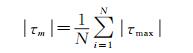 (6)
(6)
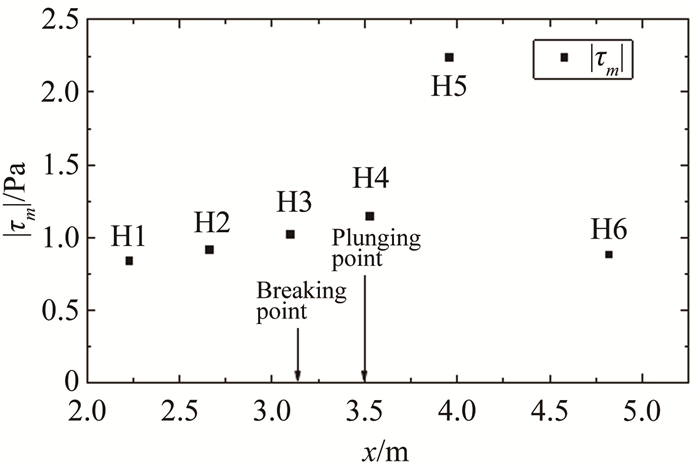
式中:|τmax|为每个波周期内出现的最大床面剪应力值,N为波浪的采样个数。图 9为斜坡沿程各断面最大床面剪应力均值的分布情况。从图中可以看出,沿程最大床面剪应力均值有向岸增大的趋势,在波浪破碎之前变化趋势较为平缓。最大床面剪应力均值在卷破水舌入射点之后的位置(H5) 会出现显著的增大,较破波点位置处(H3) 出现了约2倍的放大效应。由于缺少床面剪应力方向的信息,此极值对应的方向并不明确。
|
| 图 9 最大底部剪应力均值沿斜坡分布 Fig.9 Distribution of average maximum bed shear stress along the slope |
对于河口海岸工程中泥沙输移的问题,剪应力的方向关系到泥沙输移的方向,在波浪水槽实验中一般只需要考虑床面剪应力的正负变化,对于波浪港池中的实验,则需要对平面360°进行全向识别,因此在该传感器未来的开发中亟需解决剪应力方向识别的问题。
4 结论在波浪破碎情况下,对MEMS柔性热膜式剪应力传感器进行了测试应用实验,讨论了该传感器在破碎波作用下的工作情况,并初步探明了破碎波作用下的床面剪应力变化特征,得出如下结论:
(1) MEMS柔性热膜式剪应力传感器可以应用于破碎波作用下的床面剪应力测量。
(2) 在破波点之前可以通过ADV测得的近底流速来判断床面剪应力的方向。当波浪破碎以后,底部剪应力方向的准确判断仍然困难。
(3) 在波浪破碎之前床面剪应力变化较为平缓,在波浪破碎之后床面剪应力的波动和极值都会增大。斜坡上沿程最大床面剪应力均值的极值出现于卷破水舌入射点之后。
致谢: 西北工业大学微/纳米系统实验室马炳和教授的团队为本文的研究提供了MEMS柔性热膜式剪应力传感器和帮助,作者在此表示感谢。| [1] | 邹志利. 海岸动力学[M]. 第四版.北京: 人民交通出版社, 2009. Zou Z L. Coastal hydrodynamics[M]. 4th ed. Bejing: China Communications Press, 2009. |
| [2] | Mirfenderesk H, Young I R. Direct measurements of the bottom friction factor beneath surface gravity waves[J]. Applied Ocean Research, 2003, 25(5): 269–287. DOI:10.1016/j.apor.2004.02.002 |
| [3] | Huo G, Wang Y G, Yin B S, et al. A new measure for direct measurement of the bed shear stress of wave boundary layer in wave flume[J]. Journal of Hydrodynamics, Ser B, 2007, 19(4): 517–524. DOI:10.1016/S1001-6058(07)60148-6 |
| [4] | Pujara N, Liu P L F. Direct measurements of local bed shear stress in the presence of pressure gradients[J]. Experiments in Fluids, 2014, 55(7): 1–13. |
| [5] | Pujara N, Liu P L F, Yeh H. The swash of solitary waves on a plane beach: flow evolution, bed shear stress and run-up[J]. Journal of Fluid Mechanics, 2015, 779: 556–597. DOI:10.1017/jfm.2015.435 |
| [6] | Arnskov M M, Fredsøe J, Sumer B M. Bed shear stress measurements over a smooth bed in three-dimensional wave-current motion[J]. Coastal Engineering, 1993, 20(3): 277–316. |
| [7] | Sumer B M, Arnskov M M, Christiansen N, et al. Two-com-ponent hot-film probe for measurements of wall shear stress[J]. Experiments in Fluids, 1993, 15(6): 380–384. |
| [8] | Jensen B L, Sumer B M, Fredsøe J. Turbulent oscillatory boundary layers at high Reynolds numbers[J]. Journal of Fluid Mechanics, 1989, 206: 265–297. DOI:10.1017/S0022112089002302 |
| [9] | Carstensen S, Sumer B M, Fredsøe J. Coherent structures in wave boundary layers. part 1. oscillatory motion[J]. Journal of Fluid Mechanics, 2010, 646: 169–206. DOI:10.1017/S0022112009992825 |
| [10] | Musumeci R E, Marletta V, Andò B, et al. Measurement of wave near-bed velocity and bottom shear stress by ferrofluids[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(5): 1224–1231. DOI:10.1109/TIM.2014.2359521 |
| [11] | 梁婷, 夏云峰, 徐华, 等. 波浪作用下床面切应力测量初探[J]. 水道港口, 2010, 31(5): 425–428. Liang T, Xia Y F, Xu H, et al. Preliminary study of bed shear stress measurement under wave action[J]. Journal of Waterway and Harbor, 2010, 31(5): 425–428. |
| [12] | Xu H, Xia Y F, Ma B H, et al. Research on measurement of bed shear stress under wave-current interaction[J]. China Ocean Engineering, 2015, 29(4): 589–598. DOI:10.1007/s13344-015-0041-z |
| [13] | Boers M. Surf zone turbulence[D]. Netherlands: Delft University of Technology, 2005. |
| [14] | Deigaard R, Fredsøe J, Mikkelsen M B.Measurements of the bed shear stress in a surf zone[R]. Progress Report 73, Lyngby: Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark, 1991: 21-30. http://www.academia.edu/10624279/Beach_Stratigraphy |
| [15] | Yüksel Y, Çevik E Ö, Kapdanşli S. Bed shear stress distribution over beach profiles[J]. Journal of Coastal Research, 1998, 14(3): 1044–1053. |
| [16] | Sumer B M, Sen M B, Karagali I, et al. Flow and sediment transport induced by a plunging solitary wave[J]. Journal of Geophysical Research: Oceans, 2011, 116(C1): C01008. |
| [17] | Sumer B M, Guner H, Hansen N M, et al. Laboratory observations of flow and sediment transport induced by plunging regular waves[J]. Journal of Geophysical Research: Oceans, 2013, 118(11): 6161–6182. DOI:10.1002/2013JC009324 |
| [18] | Schlichting H, Gersten K. Boundary-layer theory[M]. 9th ed. Berlin: Springer, 2016. |
| [19] | 马炳和, 王毅, 姜澄宇, 等. 柔性热膜剪应力传感器水下测量温度修正[J]. 实验流体力学, 2014, 28(2): 39–44. Ma B H, Wang Y, Jiang C Y, et al. Temperature correction of flexible thermal shear stress sensor for underwater measurements[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 39–44. DOI:10.11729/syltlx20140006 |
| [20] | Knight D W, Patel H S. Boundary shear in smooth rectangular ducts[J]. Journal of Hydraulic Engineering, 1985, 111(1): 29–47. DOI:10.1061/(ASCE)0733-9429(1985)111:1(29) |
| [21] | Koca K, Noss C, Anlanger C, et al. Performance of the Vectrino Profiler at the sediment-water interface[J]. Journal of Hydraulic Research, 2017: 1–9. DOI:10.1080/00221686.2016.1275049.) |
| [22] | Murai Y. Frictional drag reduction by bubble injection[J]. Experiments in Fluids, 2014, 55(7): 1773. DOI:10.1007/s00348-014-1773-x |





