流体壁面剪应力(Wall Shear Stress)又被称为摩阻应力,其有效测量是精确掌握摩擦阻力的基础。同时,作为基本流动力学参量之一,其精确测量为判断边界层分离和转捩等流动状态提供了重要参考依据,对于飞行器、发动机和航行器等结构设计优化以及减阻降噪有重要指导意义[1-2]。
基于MEMS(Micro Electro -Mechanical Systems, MEMS)技术的剪应力微传感器结构尺寸小,具有高的时间和空间分辨率,能够对流体壁面剪应力进行定点精确测量,对流体壁面剪应力测量技术的发展具有重要意义。
目前,流体壁面剪应力的测量方法有直接法和间接法2种[3-4]。热膜式微传感器是一种间接的测量方法[5]。直接法测量剪应力的微传感器一般具有力敏感的浮动单元或弹性结构,根据测量原理可分为电容式、压阻式和光学式[6-13]等。压阻式剪应力微传感器受温度影响较大,需要进行温度补偿。光学式剪应力微传感器测量精度高,但整个系统相对复杂。电容式剪应力微传感器具有线性特性、测量分辨率高、动态响应快和温度影响小等优点,应用前景广阔。
Schmidt首次开展了浮动电容式剪应力微传感器的研究工作,给出了微传感器的设计制造方法和实验测试结果[14]。Pan等采用折叠梁、交叉排布梳齿结构对传感器结构进行优化,有效提高了传感器的灵敏度[15],但没有进行微传感器敏感结构设计研究。Vijay Chandrasekharan对微传感器探头结构进行了详细设计[7],但由于考虑因素繁多,导致其设计过程非常复杂,很难系统地掌握传感器探头结构与传感器性能指标之间的相互关系,设计难度较大。此外,Zhao Zhengxin和Lyu Haifeng分别对浮动电容式剪应力微传感器进行了研究[8, 16],但缺乏对传感器性能与结构间的关系研究分析。
浮动电容式剪应力微传感器探头采用经典梳齿电容敏感结构,在一定程度上与微加速度计、微机械陀螺等相似,因此可借鉴其设计方法。然而,这些MEMS微传感器敏感结构往往通过经验或试错的方法,借助计算仿真软件如ANSYS、CoventorWare、Comsol等进行结构设计[17-19]。设计过程无法明晰传感器结构参数对其性能的直接影响,而且每个设计案例必须建立各自三维模型、划分网格、有限元或边界元运算求解等,限制了设计效率。
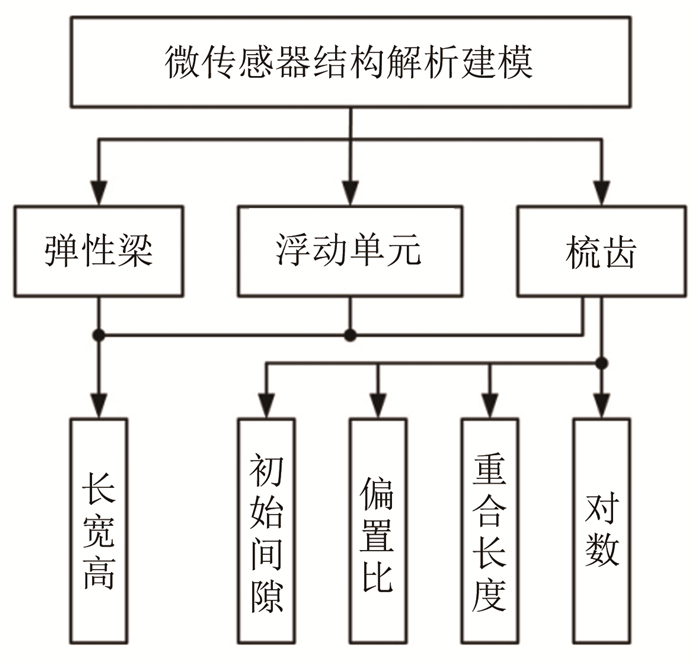
尽管前人对浮动电容式剪应力微传感器开展了大量的研究工作,但是仍没有形成系统的设计方法,缺乏对传感器综合性能与传感器探头结构间关系的详细研究。本文对浮动电容式剪应力微传感器探头结构特点和工作原理进行了研究,建立了该微传感器的结构设计的解析模型。给出了一种面向应用需求的设计方法,使该微传感器敏感探头结构的设计变得简便、高效。
1 工作原理浮动电容式剪应力微传感器在流体壁面剪应力的作用下,其浮动单元带动可动梳齿相对固定梳齿产生微小位移,使得输出电容值发生变化。通过外部电路检测电容变化量就可以直接得出剪应力的大小。
传感器探头结构主要包括悬置弹性梁、浮动单元及可动梳齿,与基体固连的固定梳齿、锚点等,如图 1所示。弹性梁支撑连接悬置的浮动单元及其两侧的可动梳齿结构,可动梳齿与固定梳齿构成多组相对的微小平板电容器,其电容值与相邻梳齿间隙大小有关。

|
| 图 1 浮动电容式剪应力微传感器结构 Fig.1 Structure of the floating element wall shear stress sensor with capacitive sensing |
微传感器设计时经常指向量程、固有频率、灵敏度、线性度和分辨率等性能指标。本文结构解析建模主要是建立弹性梁、浮动单元和梳齿等主要结构面向这些性能参数的解析解,以增加设计过程的指向性和透明性。微传感器探头主要结构及参数如图 2所示。
|
| 图 2 浮动电容式剪应力微传感器结构设计 Fig.2 Structure design forthe floating element wall shear stress sensor with capacitive sensing |
微传感器的量程和固有频率指标主要取决于弹性梁和浮动单元的结构参数,而非线性度、灵敏度和分辨率则主要取决于梳齿结构参数。
2.1 浮动单元浮动单元是传感器的敏感单元,用于“感受”流场作用在探头上表面的剪应力。该剪应力在浮动单元表面积分后,可以等效成集中力作用在弹性梁的活动端。因此,积分面积Ae是浮动单元设计的关键尺寸。一般浮动单元面积为1mm2左右,Ae太大会降低传感器的动态特性,甚至导致其失效[20]。
2.2 弹性梁微机械结构中弹性梁的设计常采用折叠梁结构,以降低刚度和提高灵敏度[21-22]。浮动电容式剪应力微传感器采用的折叠梁总刚度k可以表示为:
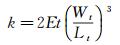 (1)
(1)
公式(1) 中E表示微传感器敏感芯片制造材料(Si)的弹性模量,Wt、Lt和t分别表示弹性梁的宽度、长度和厚度,弹性梁结构尺寸特征如图 3所示。

|
| 图 3 弹性梁结构特征尺寸 Fig.3 Dimension of folded tether |
相比于浮动单元,弹性梁上表面剪应力的影响可以忽略不计。因此,作用在传感探头上的合力可以表示为F=τAe,根据Euler-Bernoulli弯曲方程,可以得出剪应力τ与浮动单元位移δ的关系:
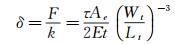 (2)
(2)
将公式(2) 变形可以得到传感器量程指标的表达式为:
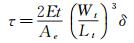 (3)
(3)
传感器固有频率由浮动单元和弹性梁共同决定:
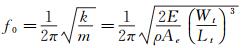 (4)
(4)
式中:ρ表示微传感器敏感探头芯片制造材料(Si)的密度。
由公式(3) 和(4) 看出,影响微传感器的量程和固有频率的主要参数是弹性梁的宽长比。固有频率解析公式(4) 中具有更少的可变参数,通过该指标要求确定弹性梁的宽长比(Wt/Lt)范围之后,然后结合量程解析公式(3) 确定微传感器探头结构厚度(t)的尺寸大小。这些已经确定的结构参数将作为已知量,用于其他结构参数的设计。
2.3 梳齿结构可动梳齿和固定梳齿分布于浮动单元两侧,构成差动电容器。差动形式可以提高器件灵敏度、改善非线性。图 4为梳齿排布示意图。
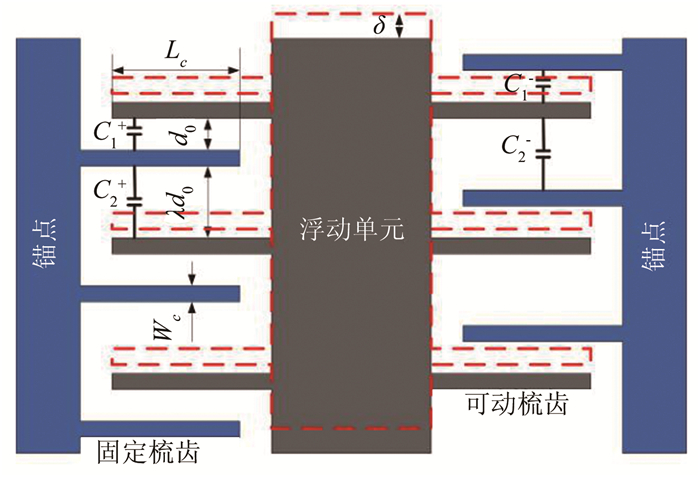
|
| 图 4 浮动电容式剪应力微传感器梳齿结构排布方式 Fig.4 Comb fingers' arrangement of the floating element wall shear stress sensor with capacitive sensing |
采用电荷放大电路对传感器电容进行检测,其原理如图 5所示。在微传感器敏感芯片探头上加载一个高频正弦载波,对梳齿电容信号进行调制。调制信号在表头经电路电荷放大、差分和滤波处理后,输入到外部电路。最终通过相干解调和低通滤波,将其还原成与输入剪应力成正比关系的直流电压信号。
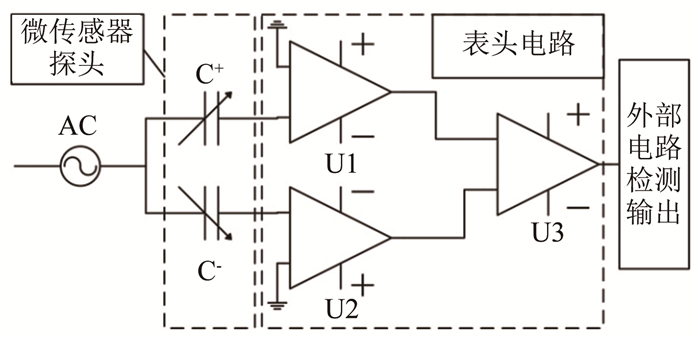
|
| 图 5 浮动电容式剪应力微传感器检测电路 Fig.5 Detection circuit of the floating element wall shear stress sensor with capacitive sensing |
当剪应力为τ时,浮动单元沿着传感器敏感方向产生位移δ,如图 4中红色虚线所示。此时梳齿电容值可以表示为:
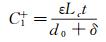 (5)
(5)
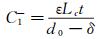 (6)
(6)
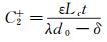 (7)
(7)
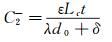 (8)
(8)
式中:ε表示空气介质的介电常数,Wc、Lc、t和d0分别表示梳齿结构的宽度、长度、高度和相邻梳齿的初始间隙,λ表示梳齿排布的偏置比,一般取值为λ=2.5~3。假设梳齿排布对数为N,容易得出浮动单元两侧电容差值可以表示为:
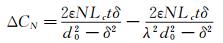 (9)
(9)
当浮动单元位移δ远小于相邻梳齿间隙d0时,将ΔCN变换后进行Taylor展开,然后忽略高阶无穷小量O(h2),可以得出:
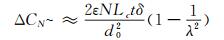 (10)
(10)
梳齿电容差值大小与浮动单元位移变化成线性关系,但截断误差引入了非线性因素。用截断误差与实际梳齿电容差值比值的百分数表示传感器的非线性度(γ),即:
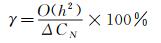 (11)
(11)
通过公式(9) 和(10) 进行求解得出微传感器的非线性度表达式为:
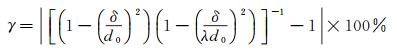 (12)
(12)
影响微传感器非线性度的参数只有δ、d0和λ。计算表明,当δ=0.1d0时,微传感器的非线性度γ约为1.2%左右。
为了增加传感器的灵敏度,在设计梳齿结构时要尽可能增加ΔCN~的值。一对梳齿沿敏感方向的排布长度为2Wc+(1+λ)d0,单排梳齿总的排布长度等于浮动单元长度Le,因此每排梳齿对数N可以表示为:
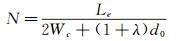 (13)
(13)
结合公式(10),在剪应力τ的作用下微传感器探头输出的电容差值变化量为:
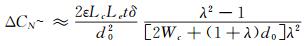 (14)
(14)
ΔCN~随λ的变化趋势是一个存在最大值的单峰连续曲线。因此一定会存在λ值,使得ΔCN~达到最大。求解得出λ的表达式为:
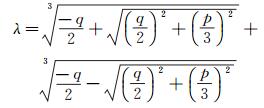 (15)
(15)
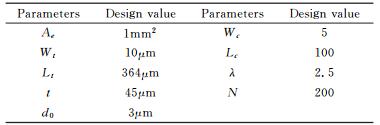
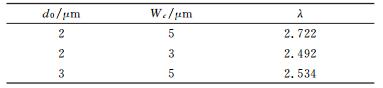
公式(15) 中p=-3,q=-(4Wc+d0)/d0,该结果是利用卡丹公式求解一元三次方程得到。表 1是常用梳齿结构参数对应的最佳偏置比。
|
用单位位移变化引起的电容差值变化量表示传感器的灵敏度(S),单位为F/m。根据公式(13) 可以得出微传感器灵敏度S的表达式为:
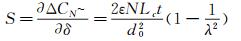 (16)
(16)
用传感器能够检测的最小剪应力值表示其分辨率(τmin),单位为Pa。微传感器分辨率很大程度上取决于电路的检测能力,用Cmin表示电路能够检测的最小电容值,联合公式(3) 和(10) 消去δ可以得出微传感器的分辨率为:
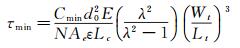 (17)
(17)
传感器结构设计解析模型建立了其结构参数与性能指标之间的相互关系,可以看出:
(1) 弹性梁的宽长比Wt/Lt和相邻梳齿初始间隙d0对微传感器性能指标的影响成高次幂函数关系,是微传感器结构设计中的重要参数。
(2) 传感器性能指标之间相互制约,应对含有结构变量最少的性能指标优先设计,在保证性能需求前提下,完成传感器设计的最佳方案。
3 设计案例下文结合具体设计案例,阐述微传感器敏感芯片探头结构设计的方法。设计过程中需要考虑传感器的指标需求、材料特性和工艺水平等因素。图 6是微传感器敏感探头结构设计过程。
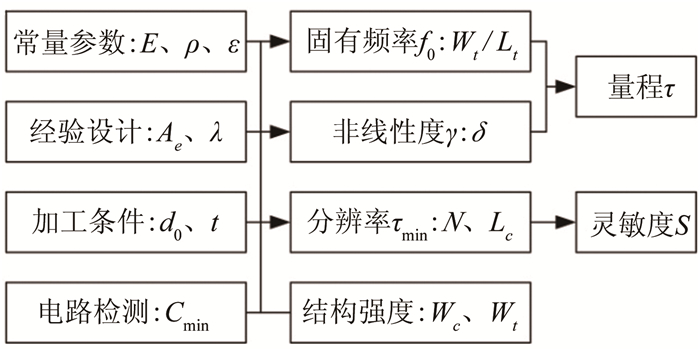
|
| 图 6 利用解析模型设计浮动电容式剪应力微传感器探头的流程 Fig.6 Design flow for the floating element wall shear stress sensor with capacitive sensing by the analytical model |
(1) 传感器的性能指标需求。
量程:60Pa
固有频率:7.2kHz
非线性度:1.2%
(2) 材料特性
选用Si材料对微传感器进行加工制造。弹性模量E=130GPa,密度ρ=2330kg/m3。
(3) 确定参数
空气的介电常数ε=8.86×10-12F/m;
浮动单元面积Ae=1mm2;
ICP刻蚀的最小线宽决定梳齿间隙d0=3μm;
在保证强度的前提下尽量增加梳齿对数,一般设定梳齿宽度和重合长度分别为5和100μm。
(4) 确定结构参数少的指标
根据公式(15) 确定最佳偏置比为λ≈2.5;
根据非线性度指标和公式(12) 确定浮动单元位移δ≤0.3μm;
根据公式(4) 确定弹性梁的宽长比Wt/Lt≥0.027;
根据公式(3) 确定器件层厚度t≥40μm。
(5) 优化传感器方案
传感器的灵敏度和分辨率一般受后端检测电路影响较大,根据梳齿排布方式给定梳齿数N=200。
微传感器探头结构设计结果如表 2所示。
图 7为微传感器探头的SEM照片。由于实际ICP加工过程中存在横向刻蚀的现象,使得弹性梁刚度降低,梳齿间隙变大,对传感器性能会造成一定的影响。
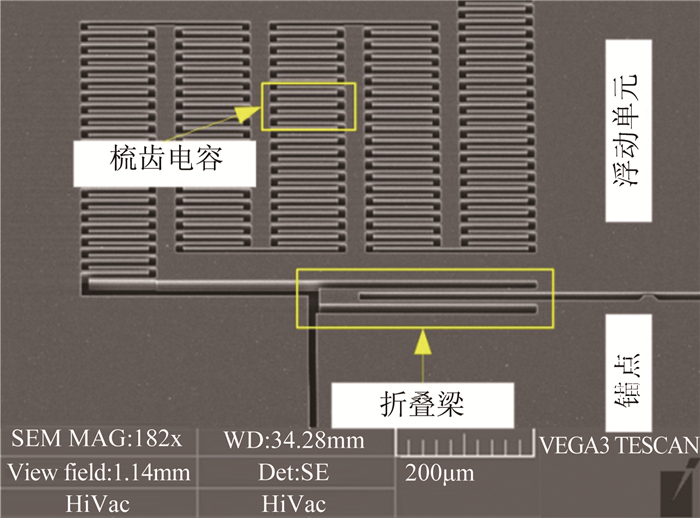
|
| 图 7 浮动电容式剪应力微传感器结构SEM照片(1/4视图) Fig.7 SEM picture of the floating element wall shear stress sensor with capacitive sensing (a quarter view) |
实验测试包括静态测试和动态测试,是在中国空气动力研究与发展中心高速所完成的。
4.1 静态测试静态测试装置如图 8所示。该装置流场控制精度高,来流速度范围0~0.67Ma,可产生最大剪应力达60Pa以上,满足浮动电容式剪应力微传感器静态测试需求。实验过程中设置马赫数变化范围0.3~0.65,剪应力最大达到65Pa左右,对实验数据进行处理后的结果如图 9所示。

|
| 图 8 MEMS壁面剪应力传感器静态标定装置 Fig.8 Static calibration apparatus for MEMS wall shear stress sensor |
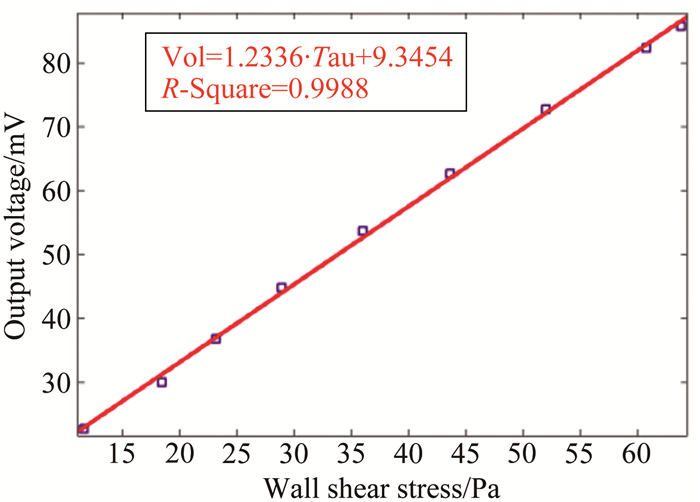
|
| 图 9 浮动电容式剪应力微传感器静态标定曲线 Fig.9 Static calibration curve of the floating element wall shear stress sensor with capacitive sensing |
可以看出,微传感器量程达到60Pa以上,实验数据线性拟合的确定系数R2=0.9988,表明微传感器具有高的线性度。通过分析计算,微传感器输出的非线性度约为1.57%,与理论结果基本相符。
4.2 动态标定采用平波管法对浮动电容式剪应力微传感器进行动态标定,标定系统如图 10所示。
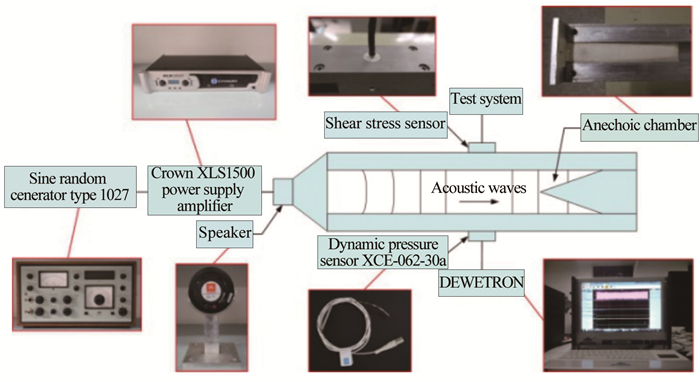
|
| 图 10 MEMS壁面剪应力传感器动态标定系统 Fig.10 Dynamic calibration system for MEMS wall shear stress sensor |
该系统主要由函数发生器、功率放大器、扬声器和脉动压力传感器等部分组成。函数发生器产生一定频率的正弦激励信号,该信号通过功率放大器驱动扬声器,进而在标定管道内产生振荡的平面声波;采用脉动压力传感器采集作用于剪应力微传感器探头的声压大小,然后计算出施加在微传感器探头上的剪应力数值。平波管中剪应力计算公式为[23]:
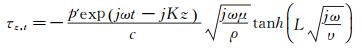 (21)
(21)
公式(21) 中p′为压力脉动量,ρ、μ、ν分别表示介质密度、动力粘度运动粘度,ω、c表示平面声波在介质中传播的频率和速度,K=ω/c为轴向波数,L表示管道中心与壁面的距离。
为了得出浮动电容式剪应力微传感器的固有频率,在不同激励频率下对传感器进行动态测试,得出相应的动态灵敏度。图 11表示微传感器动态灵敏度与激励频率之间的关系。
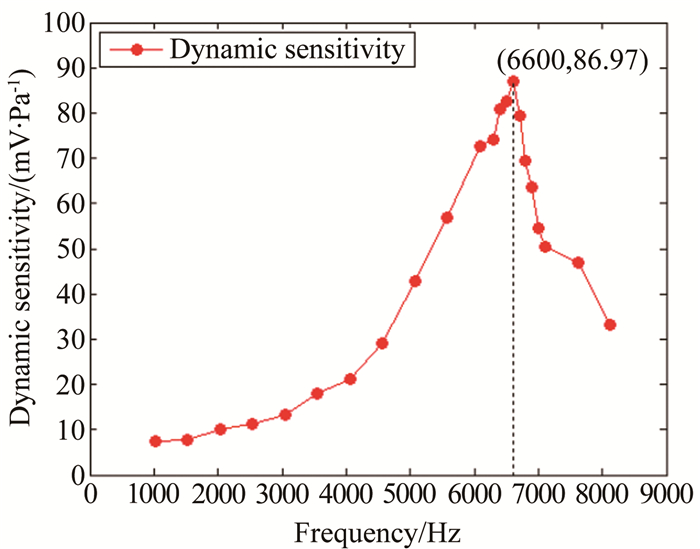
|
| 图 11 微传感器动态灵敏度与激励频率的关系 Fig.11 Relationship between dynamic sensitivity and excitation frequency of the sensor |
计算得出, 微传感器的固有频率f0=6.6kHz,小于其设计值7.2kHz,通过测量微传感器敏感芯片探头加工的实际尺寸,利用解析模型再次计算的理论固有频率约为6.8kHz,与实验结果相差在2.4%左右。
5 结论(1) 浮动电容式剪应力微传感器在流体壁面剪应力测量方面具有巨大应用潜力,测量精度高、动态性能好等特点使得其在流体边界层流动,尤其是在瞬态流场测量中具有优势。
(2) 微传感器结构设计解析模型清晰地表达了敏感芯片探头结构参数与性能指标之间的关系,可以克服传统有限元仿真法过程复杂、效率低和不透明等缺点。
(3) 设计研发案例的测试结果与理论设计基本符合,证明了该方法的有效性。
致谢: 本文由国家重大科学仪器设备开发专项流体壁面剪应力测试仪开发与应用(2013YQ040911) 资助。特别致谢中国空气动力研究与发展中心高速空气动力研究所李建强、梁锦敏等的指导与帮助。| [1] | Johansson T G, Medhi F, Naughton J W. Some problems with near-wall measurements and the determination of wall shear stress[J]. AIAA Aerodyn Meas Technol Gr Test Conf, 2006, 2: 1179–1563478110. |
| [2] | 屠恒章, 李建强, 明晓, 等. 基于MEMS传感器的高速风洞壁面剪切应力直接测量技术[J]. 实验流体力学, 2008, 22(3): 94–98. Tu H Z, Li J Q, Ming X, et al. Direct measurement technique of wall shear stress using MEMS sensors in a high-speed wind tunnel[J]. Journal of Experiemnts in Fluid Mechanics, 2008, 22(3): 94–98. |
| [3] | Naughton J W, Sheplak M. Modern developments in shear stress measurement[J]. Prog Aerosp Sci, 2002, 38: 515–570. DOI:10.1016/S0376-0421(02)00031-3 |
| [4] | Onsrud G, Persen L N, Saetran L R. On the measurement of wall shear stress[J]. Expt Fluids, 1987, 5: 11–16. |
| [5] | Ma B, Li Y, Wang L, et al. Modelling and calibration of microthermal sensor for underwater wall shear stress measurement[J]. Micro & amp; Nano Lett, 2014, 9(7): 486–489. |
| [6] | Chandrasekharan V, Sells J, Meloy J, et al. A microscale di-fferential capacitive direct wall-shear-stress sensor[J]. J Microelectromechanical Syst, 2011, 20(3): 622–635. DOI:10.1109/JMEMS.2011.2140356 |
| [7] | Chandrasekharan V, Sells J, Arnold D P, et al. Characterization of a MEMS-based floating element shear stress sensor[J]. AIAA Aerosp Sci Meet, 2009: 1–11. |
| [8] | Lyu H, Jiang C, Xiang Z, et al. Design of a micro floating element shear stress sensor[J]. Flow Meas Instrum, 2013, 30: 66–74. DOI:10.1016/j.flowmeasinst.2012.11.004 |
| [9] | Seo D, Kwon S, Bae N, et al. MEMS wall shear stress sensor for real time onboard monitoring of flow separation over a wing surface[C]. 51st AIAA Aerosp Sci Meet Incl New Horizons Forum Aerosp Expo, 2013: 1-8. |
| [10] | Ma B H, Ma C Y. A MEMS surface fence for wall shear stress measurement with high sensitivity[J]. Microsyst Technol, 2016, 22(2): 239–246. DOI:10.1007/s00542-015-2450-6 |
| [11] | Sullivan D J, Kline J F, Salamon M. An optically interrogated, microfabricated pillar array for wall shear stress sensing[C]. 50th AIAA Aerosp Sci Meet Incl New Horizons Forum Aerosp Expo, 2012: 1-12. |
| [12] | Chen T A, Mills D, Chandrasekharan V, et al. A miniaturized optical package for wall shear stress measurements in harsh environments[C]//Proceedings of SPIE-The International Society for Optical Engineering, 2014, 6113: 91130G. |
| [13] | Ayaz U K, Ioppolo T, Ötügen V. High resolution micro-optical wall shear stress sensor[J]. AIAA Aerosp Sci Meet, 2011: 1–9. |
| [14] | Schmidt A. Design and calibration of a microfabricated floating-element shear-stress sensor[J]. IEEE Trans Electron Devices, 1988, 35(6): 750–757. DOI:10.1109/16.2527 |
| [15] | Pan T, Hyman D, Mehregany M, et al. Microfabricated shear stress sensors, Part 1: design and fabrication shear stress and its measurement[J]. AIAA J, 1999, 37(1): 66–72. DOI:10.2514/2.665 |
| [16] | Zhao Z, Shin M, Gallman J M, et al. A microfabricated shear sensor array on a chip with pressure gradient calibration[J]. Sensors Actuators, A Phys, 2014, 205: 133–142. DOI:10.1016/j.sna.2013.11.002 |
| [17] | Desai A V, Haque M A. Design and fabrication of a direction sensitive MEMS shear stress sensor with high spatial and temporal resolution[J]. J Micromechanics Microengineering, 2004, 14: 1718–1725. DOI:10.1088/0960-1317/14/12/017 |
| [18] | Khankhua S, Ashraf M W, Tayyaba S, et al. Simulation of MEMS based Micro-Gyroscope using coventor ware[J]. Circuits Syst Adv Technol, 2011: 22–25. |
| [19] | Anadkat N, Rangachar J S. Simulation based analysis of capacitive pressure sensor with COMSOL multiphysics[J]. Int J Eng Res Technol. (IJERT), 2015, 4(4): 848–852. |
| [20] | 吕海峰, 姜澄宇, 邓进军, 等. 用于壁面切应力测量的微传感器设计[J]. 机械工程学报, 2010, 46(24): 54–60. Lyu H F, Jiang C Y, Deng J J, et al. Design of micro sensor for wall shear stress measurement[J]. Journal of Mechanical Engineering, 2010, 46(24): 54–60. |
| [21] | Legtenberg R, Groeneveld A W, Elwenspoek M. Comb-drive actuators for large displacements[J]. J Micromechanics Microengineering, 1996, 6(3): 320–329. DOI:10.1088/0960-1317/6/3/004 |
| [22] | Zhou G, Dowd P. Tilted folded-beam suspension for extending the stable travel range of comb-drive actuators[J]. J Micromechanics Microengineering, 2002, 13(2): 178–183. |
| [23] | Sheplak M, Padmanabhan A, Schmidt M A, et al. Dynamic calibration of a shear-stress sensor using stokes-layer excitation[J]. AIAA J, 2001, 39(5): 819–823. DOI:10.2514/2.1415 |