城市化建设过程中,城市郊区兴建大量的工业厂房等低矮建筑物。对于来自于城市中心方向的强风,这些低矮建筑所处的地貌将由城市中心的粗糙地貌转变为郊区的平坦地貌,若建筑物所处地距离2种地貌变化点较近,处于过渡边界层内时,建筑物表面风压将受到2种地貌的复合影响。
国内外学者已对非均匀地貌大气边界层进行了较为深入的研究,Logan[1]指出当地貌由粗糙地貌转变为平坦地貌时,大气边界层会随着下游平坦地貌的发展逐渐分为3个子边界层,依次为外边界层、过渡边界层和平衡边界层,其中过渡边界层受到上下游地貌共同影响。文献[2-4]分别提出了非均匀地貌下平均风速剖面模型,并不断得到完善。文献[5]利用边界层梯度高度随地貌发展距离公式[6-7]提出多种复合地貌下的风速剖面及湍流度剖面模型。文献[8]采用风速实测方法,对比分析了临海地区在不同风向下形成的多种地貌的地貌粗糙长度及平均风速剖面。文献[9-10]利用风洞试验方法,研究了二维山体地貌分布下的平均风速与湍流强度,指出山后气流分离区域的风场特性与山体坡度直接相关,同时还受山体表面粗糙度和来流湍流影响。文献[11]对目前非均匀大气边界层的研究进展和问题进行了探讨,指出地表的非均匀性会以多种方式对大气边界层产生影响,引起地表湍流变化。
与此同时,少量学者开展了不同地貌和非均匀地貌下低矮建筑物风荷载特性研究。文献[12]指出在不同地貌类型下,单个鞍形屋盖结构的平均风压系数和风压系数均方根存在较大差异,地貌越粗糙屋面平均风压系数幅值越小,风压系数均方根越大。文献[5]通过风洞试验,研究了在上游4km范围内,多种地貌类型组合下,单个双坡屋面风压特性变化规律,指出模型上游300~400m长度范围内的粗糙元对双坡屋面风压值影响最大。文献[13]通过风洞试验指出,在上游均匀地貌风场中布置棱柱体群,来流沿风向发展15倍的模型宽度后,棱柱体表面风压系数达到稳定。中国《建筑结构荷载规范》[14]和美国ASCE-7[15]给出了局部地貌(山峰或山坡)引起的来流风速修正方法。美国ASCE-7[15]对于非均匀地貌,仅对来流风压的高度系数进行了初略考虑,建议取两类地貌中的较大值,而未考虑非均匀地貌对建筑物风压分布的可能影响。
鉴于目前对非均匀地貌下的低矮建筑物风荷载特性研究较少,本文选取应用较为广泛的平屋面建筑物作为研究对象,利用风洞试验,模拟由粗糙地貌变为平坦地貌的非均匀地貌大气边界层,并通过测压试验,研究建筑物距地貌变化点不同距离时,非均匀地貌边界层内单个平屋面建筑屋面的风压变化规律。
1 风洞试验及数据处理方法 1.1 风洞试验概况风洞试验在北京交通大学回流式风洞进行,试验段尺寸为长15.0m×宽3.0m×高2.0m。风洞试验时,利用尖劈、粗糙元和挡板模拟大气边界层,上游和下游采用不同高度和密度的粗糙元模拟非均匀地貌。
测压试验对象为平屋面建筑,风场和几何模型缩尺比为1:200,模型尺寸为30cm(长)×20cm(宽)× 10cm(高),本文主要研究屋面风压特性,屋面测点59个,各墙面测点48个,共计测点107个,在屋面边缘处测压点加密,屋面测压点和风向角定义如图 1所示。试验风向角在0°~90°内以10°为间隔,并加测45°风向角,共计11个风向角。测压试验的采样频率为312Hz,测压结果按照文献[16]所述方法修正测压管道系统引起的信号畸变。图 2为风洞试验照片。图 3为非均匀地貌边界层和测压试验模型布置图,在非均匀地貌下,不断地改变建筑物的位置,建筑物中心离地貌改变点的距离S分别取0.7、0.9、1.1、1.3、1.5、1.9、2.3、2.7和3.1m。整个试验共计121个工况。
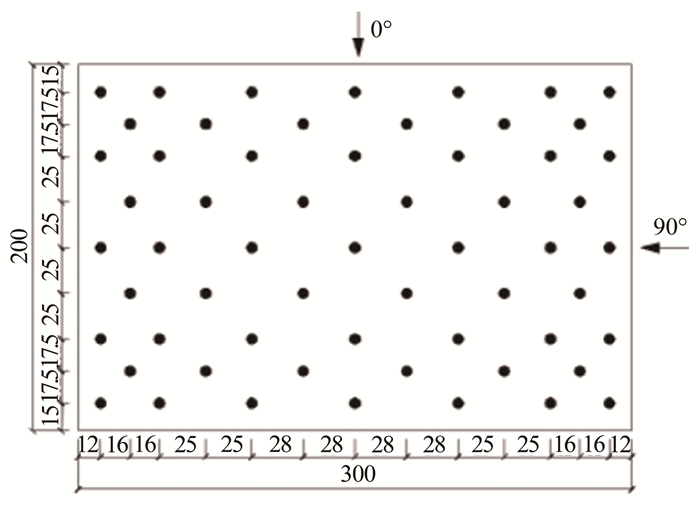
|
| 图 1 屋面测压点布置 Fig.1 Arrangement of pressure taps |

|
| 图 2 试验照片 Fig.2 Experimental photo |
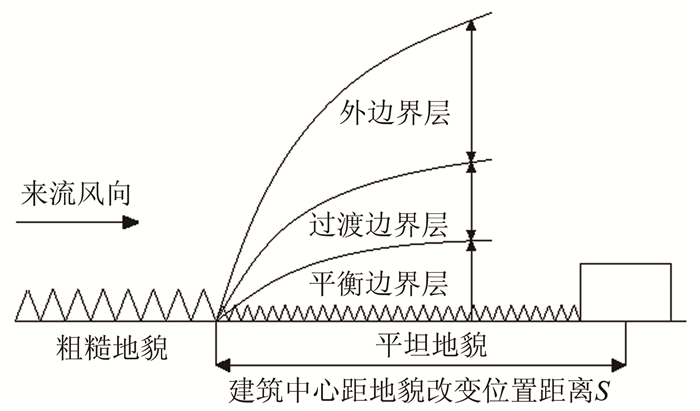
|
| 图 3 地貌和模型布置 Fig.3 Arrangement of building and terrain |
为综合评价过渡边界层内单体平屋面风压特性,定义两类测点风压系数,分别为Cpi0(t)、Cpi0′(t):
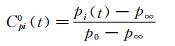 (1)
(1)
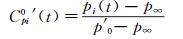 (2)
(2)
式中:pi(t)为t时刻测点i处的风压值;p0为模型位置参考高度处的总压;p′0为上游粗糙地貌风场充分发展(可取地貌变化点处,不是模型位置)位置参考高度处的总压;p∞为参考高度处的静压。两类风压系数的参考高度均为屋檐高度处。
第一类风压系数即为传统方法定义的风压系数,主要评价非均匀地貌对屋面风压分布的影响,剔除了地貌变化对来流动压的影响。第二类风压系数的定义方式,相当于在第一类风压系数的基础上,同时考虑了地貌对来流动压的影响,适合工程评价,综合反映非均匀地貌对屋面实际所受风荷载的影响。
同时,考虑到非均匀地貌对屋面不同区域风压的影响不同,为了定量评价地貌变换对屋面整体风荷载的影响,定义屋面整体平均风压系数比例系数:
 (3)
(3)
式中: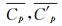
文献[1]指出,当来流风由粗糙地貌经过平坦地貌时,大气边界层会发展为3个子边界层,如图 3所示。最下层为平衡边界层,仅受到下游平坦地貌影响;中间层为过渡边界层,受到粗糙地貌和平坦地貌的共同影响;最外层为外边界层,仅受到粗糙地貌影响。平衡及过渡边界层高度均随着下游地貌发展逐渐增大。当下游地貌发展距离足够大时,则地貌已发展完全,大气边界层内的风场特性仅由该地貌决定。
风洞试验过程中,利用尖劈,挡板及粗糙元模拟了均匀粗糙地貌风场和均匀平坦地貌风场,它们的平均风速剖面指数律指数分别为0.228和0.108。
非均匀地貌模拟的工程背景是建设在城市郊区的低矮建筑,地貌由市区的粗糙地貌变化为郊区的平坦地貌。在模拟过程中,应确保地貌改变点位置处,上游粗糙地貌风场已充分发展,即平均风速剖面及湍流度剖面保持稳定。图 4给出了粗糙均匀地貌下从尖劈位置后7.2~11.8m范围内,7个位置的平均风速剖面及湍流度剖面。可以看出,自尖劈位置后8.8m处之后,平均风速剖面及湍流剖面趋于稳定,即粗糙均匀地貌风场发展完全,可将该位置作为地貌变化的改变点,布置下游平坦地貌。
|
| 图 4 粗糙地貌平均风速和湍流度 Fig.4 Mean velocity and turbulence intensity in rough terrain |
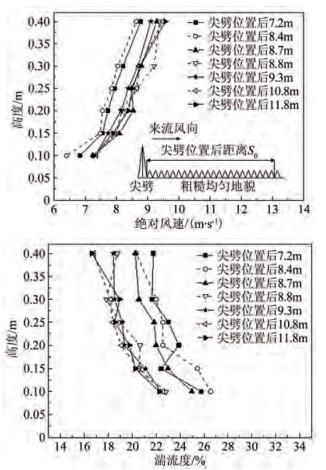
图 5给出了非均匀地貌条件下,距离地貌改变点0~3.4m范围内,7个位置的平均风速剖面和湍流度剖面变化图,可以看出:在所研究的距离范围内,上部高度范围一直主要受上游粗糙地貌影响,风速和湍流度基本保持不变,下部高度范围(约0.2m高度以下)呈现了从受上游地貌向受下游地貌影响的发展过程,平均风速逐渐增大,湍流度逐渐减小。
|
| 图 5 非均匀地貌平均风速和湍流度 Fig.5 Mean velocity and turbulence intensity in heterogeneous terrain |
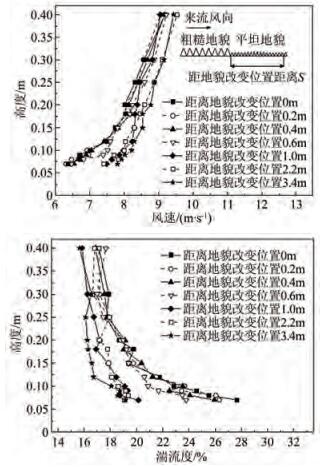
建筑物模型高度为0.1m,图 6给出了高度0.1和0.4m这2个代表性高度处平均风速和湍流度随着地貌发展的变化规律,图中给出的是与上游均匀粗糙地貌下对应高度处的比值,可以看出:0.4m高度处的平均风速及湍流度变化率基本在1.0左右,不受下游新地貌影响,即此高度始终位于外边界层范围内。在0.1m高度处,在距离地貌改变点0.4m之内,平均风速及湍流度变化较小,与上游地貌数值相近,说明处于外边界层范围内;距地貌变化点0.4~1.2m范围内,平均风速及湍流度随着离地貌变化点的距离改变发生明显变化,说明处于非均匀风场过渡边界层内;距地貌变化点距离大于1.2m之后,平均风速和湍流度变化缓慢并趋于稳定,说明处于由下游地貌决定的平衡边界层内。以上结果相当于说明:换算到原形地貌,对于高度20m处,距离地貌变化点约80m范围内,主要受上游地貌控制,处于外边界层范围;距离地貌变化点约80~240m范围内,受2种地貌共同作用,处于过渡边界层范围;但距离地貌变化点大于240m时,主要受下游地貌影响,处于平衡边界层范围。
|
| 图 6 典型高度处平均风速和湍流度 Fig.6 Mean velocity and turbulence intensity at typical heights |
下文主要针对0°风向,分析两类均匀地貌和非均匀地貌条件下,平屋面建筑的屋面平均风压系数、均方根风压系数和整体平均风压系数的变化规律。
3.1 两类均匀地貌下的屋面风压分布图 7给出了粗糙均匀地貌下,屋面的平均风压系数和均方根风压系数分布图,图 8为两均匀地貌下屋面各测点风压系数对比图,可以看出:平均风压系数的变化趋势和均方根风压系数相似,均是屋面迎风分离区最大,沿着顺风向幅值逐渐减小,平均风压系数变化梯度明显大于均方根风压系数;除屋面迎风下游区粗糙地貌下的平均风压系数幅值略小于平坦地貌,屋面其它位置平均风压系数幅值和脉动风压系数都是粗糙地貌明显大于平坦地貌;地貌对脉动风压系数的影响明显大于对平均风压系数的影响,并且在均方根风压系数大的气动分离位置影响更大。

|
| 图 7 粗糙均匀地貌下的风压系数 Fig.7 Wind pressure coefficients in rough terrain |
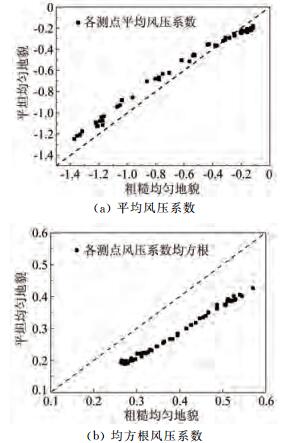
|
| 图 8 两类均匀地貌下的风压系数 Fig.8 Pressure coefficients of two uniform terrains |
图 9给出了在0°~90°风向范围内,两类均匀地貌下的屋面整体平均风压系数,可以看出:两类均匀地貌屋面整体平均风压系数幅值随着风向角的增大而减小,粗糙均匀地貌屋面整体风压系数最小值为-0.60;在0°~45°风向范围内,粗糙地貌条件下的屋面整体风压系数幅值明显大于平坦地貌,两者相差约10%,当风向大于45°,不同地貌产生的风压系数值差别较小。
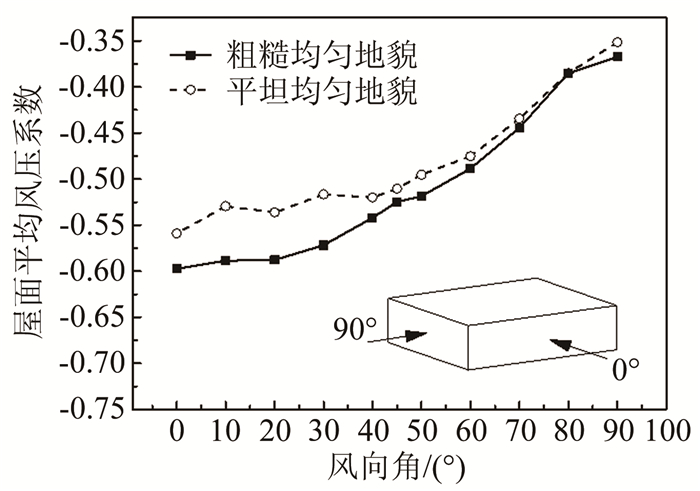
|
| 图 9 屋面整体平均风压系数 Fig.9 Mean pressure coefficient of the whole roof |
图 10和11为0°风向下,建筑中心距地貌改变点6个不同位置处,屋面中心断面测点分别按照式(1) 和(2) 两类定义方式的平均风压系数和均方根风压系数的变化规律,其中当距离大于1.9m时,屋面风压系数已经趋于稳定,图中未给出该部分结果。从以建筑物位置动压为无量纲化的风压系数结果,可以看出:地貌变化对均方根风压系数有较大影响,随着距地貌变化点距离的增大,屋面均方根风压系数逐渐减小,当离地貌改变点距离大于1.3m后,趋于稳定;地貌对平均风压系数的影响小于均方根风压系数,从上游粗糙地貌变化到过渡边界层范围内,屋面迎风分离区平均风压系数幅值显著减小,屋面迎风下游区负压幅值减小,迅速接近于由下游地貌决定的平衡边界层的风压试验结果,在过渡边界层范围内(建筑中心离地貌改变点0.7~1.3m范围内)变化较小,随着距离地貌变化点的增大,平均风压系数幅值略有减小。从以上游粗糙地貌的动压无量纲化得到的风压系数,可以看出:从粗糙地貌变化到平坦地貌,来流动压增大,但是以来流为参考的风压系数幅值减小,两者共同作用导致从受上游影响的外边界层变化到非均匀地貌过渡边界层和平衡边界层的过程中,迎风气动分离负压区平均风压系数值变化很小,在屋面迎风下游负压区幅值增加,均方根风压系数在迎风负压区幅值减小,从粗糙地貌到刚进入过渡边界层范围内,风压系数值变化显著,但进入过渡边界层范围后,随着离地貌变化点的距离增大,风压系数值变化很小。这一结论对工程中评估地貌变化对建筑物屋面风荷载的影响十分重要,即在上游基本风压相同的条件下,从粗糙地貌变化为平坦地貌,与均匀粗糙地貌相比,建筑物屋面迎风负压分离区平均风荷载变化较小,而脉动风荷载变化稍大且数值变小。

|
| 图 10 屋面中心断面测点平均风压系数 Fig.10 Mean pressure coefficients of roof center section |

|
| 图 11 屋面中心断面测点均方根风压系数 Fig.11 RMS pressure coefficients of roof center section |
图 12给出了离地貌改变点6个不同位置处,0°~90°风向范围内,屋面整体平均风压系数比例系数Rmean及R′mean,可以看出:各风向角下,屋面风压系数比例系数Rmean基本保持不变,其主要原因如图 10(a)所示,随着离地貌变化点的距离增大,屋面迎风分离区负压幅值减小,但迎风下游区域幅值增大,导致整个屋面数值变化不大,而且在过渡边界层范围内,平均风压系数变化较小;各风向下,屋面整体平均风压系数比例系数R′mean在过渡边界层内(建筑中心离地貌改变点0.7~1.3m范围内)增长较快,建筑中心离地貌改变点距离大于1.3m的范围,R′mean基本保持稳定,为1.17左右,且R′mean随风向角变化并不敏感,结合图 12(a)和非均匀边界层模拟结果图 5,说明非均匀地貌对屋面整体平均风荷载的主要影响因素是来流动压变化。
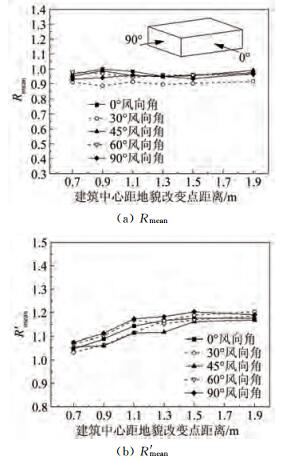
|
| 图 12 非均匀地貌屋面整体平均风压系数 Fig.12 Mean pressure coefficient of whole roof in heterogeneous terrain |
本文利用风洞试验,模拟了非均匀地貌大气边界层,采用刚性模型测压试验,研究了两类均匀地貌和非均匀地貌下,单个平屋面建筑(长:宽:高=3 :2 :1) 的屋面风压特性,得到以下主要结论:
(1) 在均匀粗糙地貌下,平屋面绝大多数位置平均风压系数幅值和脉动风压系数大于均匀平坦地貌,且脉动风压系数差别更大。
(2) 从粗糙地貌变化为平坦地貌的非均匀地貌中,以建筑物位置处动压为参考,随着距地貌变化点的距离增大,脉动风压系数逐渐减小且变化显著,但平均风压系数变化较小。
(3) 从粗糙地貌变化为平坦地貌的非均匀地貌中,以上游粗糙地貌动压为参考,随着距地貌变化点的距离增大,屋面迎风分离区平均风压变化较小,迎风下游风压幅值增大,脉动风压幅值略有减小,但在过渡边界层范围内变化较小。屋面整体平均风荷载的主要影响因素是来流动压变化。
| [1] | Logan E, Fichtl G H. Rough-to-smooth transition of an equilibrium neutral constant stress layer[J]. Boundary-Layer Meteorology, 1975, 8(3): 525–528. |
| [2] | Deaves D M. Terrain-dependence of longitudinal R. M. S. velocities in the neutral atmosphere[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8(3): 259–274. DOI:10.1016/0167-6105(81)90025-8 |
| [3] | Porté-Agel M A F. A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions[J]. Journal of Turbulence, 2012, 13(23): 1–18. |
| [4] | Bradley E F. A micrometeorological study of velocity profiles and surface drag in the region modified by a change in surface roughness[J]. Quarterly Journal of the Royal Meteorological Society, 1968, 94(401): 361–379. DOI:10.1002/(ISSN)1477-870X |
| [5] | Wang K. Modeling terrain effects and application to the wind loading of low buildings[D]. Montreal: Concordia University, 2005. |
| [6] | Lettau H. Note on aerodynamic roughness-parameter estimation on the basis of roughness-element description[J]. Journal of Applied Meteorology and Climatology, 1969, 8(5): 828–832. DOI:10.1175/1520-0450(1969)008<0828:NOARPE>2.0.CO;2 |
| [7] | Sill B L, Fang C. Effect of upstream roughness element distribution on wind loads on low rise structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 36: 1289–1297. DOI:10.1016/0167-6105(90)90125-V |
| [8] | Panofsky H A, Petersen E L. Wind profiles and change of terrain roughness at Risø[J]. Quarterly Journal of the Royal Meteorological Society, 1972, 98(418): 845–854. |
| [9] | Cao S, Tamura T. Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(1): 1–19. DOI:10.1016/j.jweia.2005.10.001 |
| [10] | Cao S, Tamura T. Effects of roughness blocks on atmospheric boundary layer flow over a two-dimensional low hill with/without sudden roughness change[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 679–695. DOI:10.1016/j.jweia.2007.01.002 |
| [11] | 刘熙明, 胡非. 大气边界层的研究——从均匀到非均匀[J]. 气象与减灾研究, 2007, 30(2): 44–51. Liu X M, Hu F. Atmospheric Boundary Layer(ABL) research: from homogeneous to heterogeneous[J]. Meteorology and Disaster Reduction Research, 2007, 30(2): 44–51. |
| [12] | Liu M, Chen X, Yang Q. Characteristics of dynamic pressures on a saddle type roof in various boundary layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 150: 1–14. DOI:10.1016/j.jweia.2015.11.012 |
| [13] | Yong C K, Yoshida A, Tamura Y. Characteristics of surface wind pressures on low-rise building located among large group of surrounding buildings[J]. Engineering Structures, 2012, 35: 18–28. DOI:10.1016/j.engstruct.2011.10.024 |
| [14] | 中国建筑科学研究院. GB 50009—2012建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012: 31-33. China Academy of Building Research. GB 50009—2012 load code for the design of building structures[S]. Beijing: China Architecture and Building Press, 2012: 31-33. |
| [15] | ASCE Standard. ASCE 7-10 Minimum design loads for buildings and other structures[S]. American Society of Civil Engineers, 2010: 246-254. |
| [16] | 陈波, 骆盼育, 杨庆山. 测压管道系统频响函数及对风效应的影响[J]. 振动与冲击, 2014, 33(3): 130–134. Chen B, Luo P Y, Yang Q S. Frequency response function of a pressure measurement pipe system and its effect on structural wind effects[J]. Journal of Vibration and Shock, 2014, 33(3): 130–134. |



