2. 风工程四川省重点实验室, 成都 610031
2. Key Laboratory for Wind Engineering of Sichuan Province, Chengdu 610031, China
Scanlan引入颤振导数[1]的概念建立了桥梁线性颤振分析框架,其基于线性化假设,将桥梁断面的自激气动力表达为运动状态向量的线性函数。由于Scanlan颤振理论物理意义明确,现广泛应用于桥梁的气动弹性分析。随着技术的进步,桥梁正朝向超大跨度发展,其在强风下的振幅也显著增加,因此在小振幅下提出的线性自激气动力假设在大振幅条件下可能存在一定的局限性。
Bocciolone[2]通过试验证明,在大迎角大幅振动条件下,自激气动力的线性化假设可能会与实际情况存在较大差异。Falco[3]在利用强迫振动装置对墨西拿海峡大桥一号断面进行节段模型试验研究时,观测到明显的非线性高阶自激气动力项。Matsunmoto[11]研究了2种矩形断面气动自激力受运动模态的影响,发现了气动力的不可叠加非线性。Diana对墨西拿海峡大桥节段模型的非线性气动力进行了研究[4],提出了描述非线性气动迟滞效应的数学模型[5-7]。陈政清[8]在利用强迫振动装置进行3种桥梁断面的颤振导数识别研究时,观察到自激气动力中存在明显的高阶谐波分量,尤其对于钝体断面,高阶谐波分量所占比例接近20%。廖海黎和王骑[9-10]在流线型箱梁节段模型的风洞试验研究时发现,在大振幅、大迎角条件下,高阶谐波分量显著。陈政清[8]对平板、钝体断面颤振导数的影响因素进行了研究,结果显示在一定折算风速范围内,颤振导数受振幅和频率的影响不大。Noda[12]采用分状态强迫振动测压方法,研究了振幅对矩形断面颤振导数的影响,表明扭转振幅对A2*的影响较大,这种影响主要是由流动分离点的不同引起的。
对于实际超大跨度桥梁而言,主梁往往采用流线型箱梁断面形式。这种流线型箱梁断面在不同振幅、不同迎角条件下的气动弹性行为对大跨度桥梁的颤振研究至关重要[13]。目前,关于振幅对流线型箱梁断面自激气动力的影响研究相对较少。本文利用强迫振动设备和节段模型风洞试验,研究了流线型箱梁断面自激气动力随迎角、振幅的变化规律,明确了线性气动力适用的振幅和迎角范围。
1 强迫振动测压试验桥梁节段模型强迫振动系统具有4套伺服电机驱动系统,可单独驱动节段模型作单自由度竖向或扭转运动,也可联合运动模拟弯扭耦合振动。驱动时可实现固定振幅、固定频率的稳态振动,也可实现变振幅、变频率的任意运动。该装置安装在西南交通大学XNJD-1风洞高速试验段内,如图 1所示,强迫振动装置分别安放在风洞外侧,模型的有效长度为1.5m,以保证模型的整体刚度。

|
| 图 1 强迫振动法测压风洞试验 Fig.1 Wind tunnel measuring pressure test based on forced vibration method |
试验模型选取南京长江四桥的流线型箱梁断面,缩尺比为1:70,高0.05m,宽0.554m,长1.5m,采用玻璃钢纤维和碳纤维制作。模型断面上布置60个测压点,具体尺寸如图 2所示。压力测试系统包括DSM3400主机和ZOC33压力扫描模块,可对测点进行压力测量,采样频率设置为256Hz,采样时间为32s。气动力在不同时刻对应的位移由强迫振动装置的测量系统采集。试验中,通过设置不同的振幅和迎角来研究这些因素对流线型箱梁自激气动力的影响。

|
| 图 2 断面测点布置图(单位:mm) Fig.2 Layout of section measuring points (unit: mm) |
由南京长江四桥全桥气弹模型颤振稳定性试验结果可知[14],南京长江四桥的颤振风速为74.1m/s,相应的折算风速为7.42m/s。因此本次试验选取颤振风速附近的一个折算风速(7.37m/s)进行。以下章节中数据图若不做特别说明,均为在此折算风速条件下的结果。
2 自激气动力分析方法试验中,当桥梁断面单自由度简谐运动时,若断面产生的自激气动力效应不显著,那么自激气动力会表现为与激振频率一致的单一谐波。若存在非线性自激气动力分量,那么自激气动力将包含整数倍的高次谐波分量。该过程中,其自激气动力可以统一表示为以下谐波模型[10]:
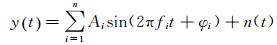 (1)
(1)
式中:Ai、fi、φi分别为各谐波信号的幅值、频率和相位;n(t)为噪声。
根据自激气动力信号的这种谐波特性,在对其进行分析时,可以利用快速傅里叶变换(FFT)初步确定自激气动力的频谱特性。然后,通过非线性最小二乘法识别出谐波参数(振幅、频率和相位),以重构气动力。在此基础之上,计算了各阶次谐波分量的比例,明确了非线性谐波分量存在的振幅和迎角范围。最后分别讨论了扭转和竖向振动振幅对颤振导数的影响。
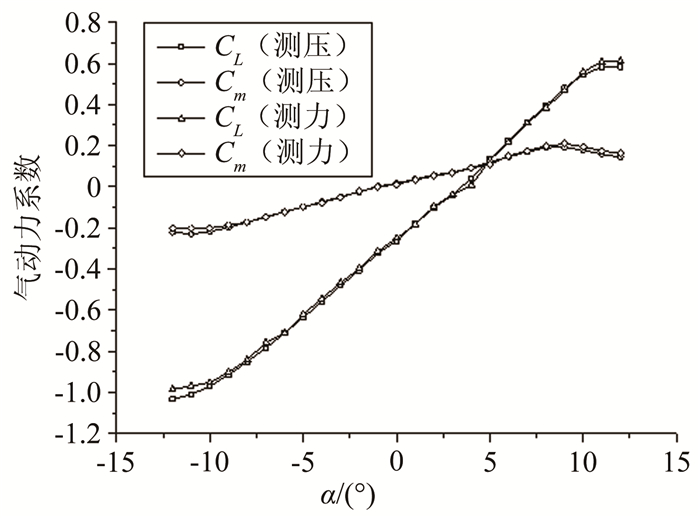
3 试验结果及分析 3.1 模型静风系数正式试验前为检验模型及测试系统性能,进行了不同风迎角下模型静风力系数的测试。图 3为模型的升力系数CL和力矩系数Cm在不同风迎角下的测试结果。从图中可以看出,在风迎角-12°~12°范围内,升力系数的斜率一直为正(∂CL/∂α>0)。升力在α=12°时开始出现转折,可认为升力失速的风迎角应该在12°左右。力矩在α=0°时开始变为正值,并在风迎角达到9°时升力矩达到最大,随后开始下降,此时力矩失速。图 3的对比结果表明,通过测压积分获得的升力和力矩系数与采用动态天平直接测试的结果保持一致[15]。因此本试验测试系统输出数据是可信的。
|
| 图 3 不同迎角对应的静风系数 Fig.3 Static aerodynamic force coefficients at different angles |
在迎角α=0°,试验风速U=10m/s条件下,对7种不同振幅进行研究。振幅分别设置为At=2°、4°、6°、8°、10°、12°和14°。振动频率设置为ft=2.45Hz,模型相应的无量纲折算风速为Vt*=7.37。此外,为研究迎角的影响,对At=10°,在α=±5°条件下也进行了试验。
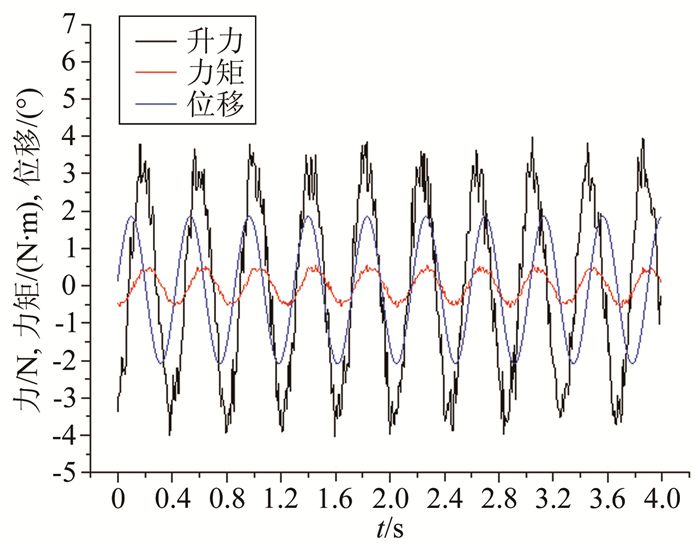
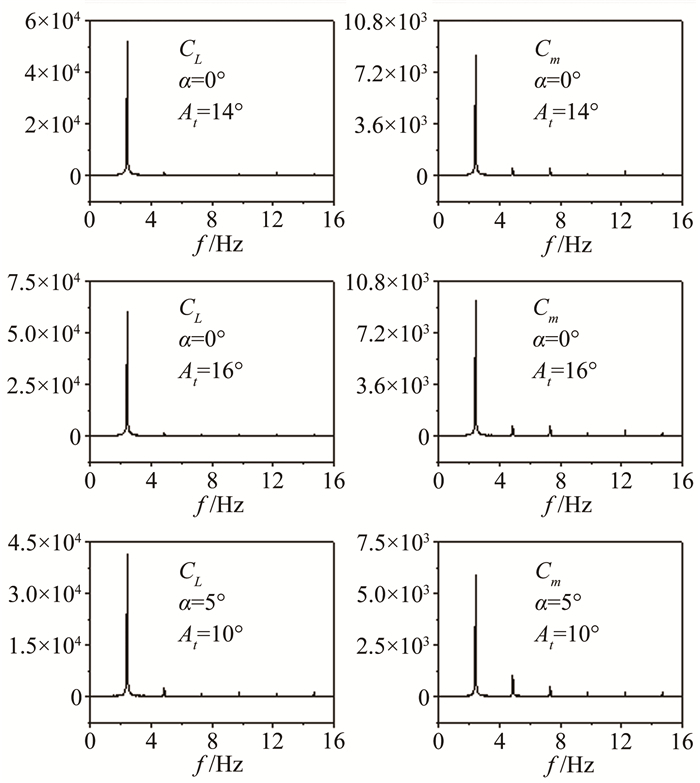
图 4为2°振幅下力和位移的同步测试时程曲线。对不同测试工况获得的自激气动力时程进行频谱分析显示,小振幅下模型自激气动力主要以基波为主;大振幅、大迎角下,自激气动力具有明显的非线性特性,谐波分量基本以1~3阶为主。图 5为非线性特性较强的气动力频谱(振幅较大)。采用最小二乘法对自激气动力的前3阶谐波幅值比例进行定量分析,不同试验条件下自激气动力基波幅值比例如图 6所示。
|
| 图 4 升力、力矩和位移时程曲线(α=0°, At=2°) Fig.4 History of lift/moment/displacement(α=0°, At=2°) |
|
| 图 5 单自由度扭转振动中自激气动力频谱 Fig.5 Frequency spectrum of motion-induced aerodynamic force in single-freedom torsional vibration |
|
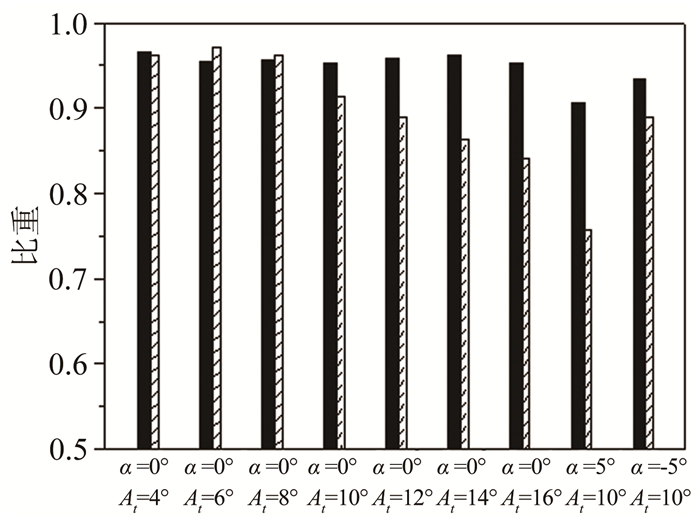
| 图 6 单自由度扭转振动中自激气动力基波幅值比例 Fig.6 First harmonic amplitude proportion of self-excited force in single-freedom torsional vibration 注:“黑色阴影”代表升力,“斜划线”代表力矩 |
迎角α=0°时,对于所有测试工况,升力的基波幅值所占比例均在95%以上,然而对于力矩,情况则不同。At=2°、5°和8°时,力矩基波幅值比例均在95%以上,而随着振幅的增大,其比例逐渐减小,非线性谐波比例逐渐增加。在At=10°时,力矩的高阶谐波幅值比例为9%,At=16°时,力矩的高阶谐波幅值比例已达到16%。此结果表明,对于流线型箱梁,单自由度大扭转振幅对其自激气动力非线性特性影响显著。为方便表述,此处定义自激气动力中基波幅值比例占95%的扭转振幅为“线性振幅”,则α=0°时,At=4°、6°和8°均处于“线性振幅”范围内(2°也在此范围内,未具体列出,其代表性时程曲线如图 4所示)。
+5°迎角对自激气动力也有较大影响。随着迎角的增大,自激气动力的基波幅值比例减小,高次谐波比例增大。在迎角α=5°时,升力和力矩的高阶谐波幅值比例分别达到10%和25%。α=-5°时,升力和力矩的高阶谐波幅值比例分别达到7%和12%。由此可知,大迎角和大振幅会显著增大流线型箱梁自激气动力中非线性谐波分量的比例。同时,在+5°迎角和8°扭转振幅以内,气动力中高次谐波分量不明显,故文中未具体列出相应结果。
3.3 单自由度竖向振动单自由度竖向振动试验,在α=0°,U=10m/s条件下,对7种不同振幅进行研究。振幅分别设置为Av=5、8、11、14、17、20和23mm。振动频率设置为fv=2.45Hz,模型相应的无量纲折算风速为Vv*=7.37。同样,为研究迎角的影响,取Av=11mm,在α=±5°条件下进行了对应的试验。
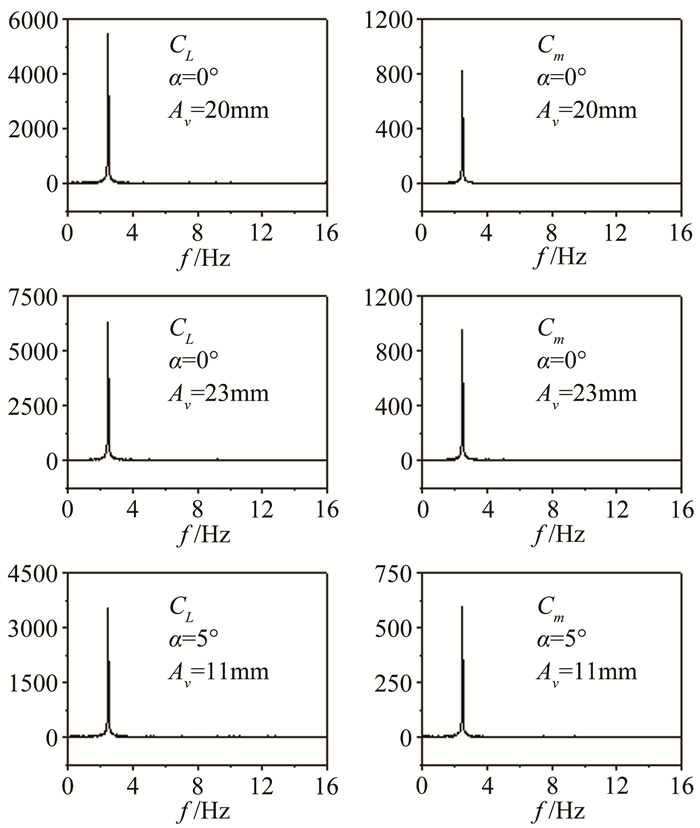
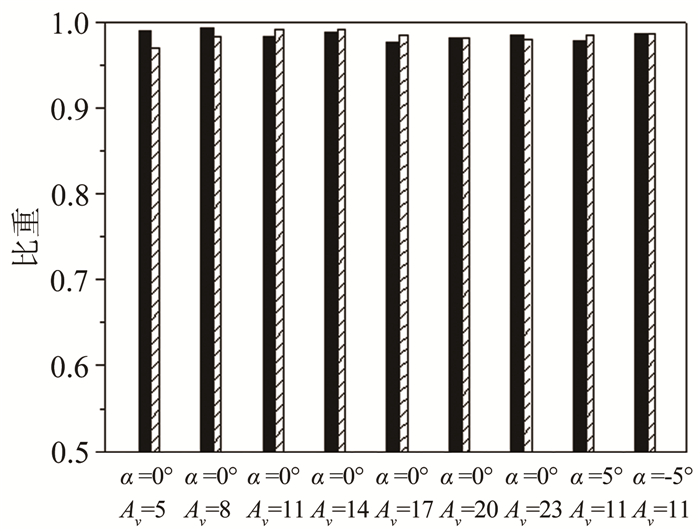
对试验得到的自激气动力信号进行频谱分析(见图 7)。分析结果显示,对所有工况,几乎观测不到高阶谐波的存在。同样对前3阶自激气动力谐波幅值比例进行定量分析发现(见图 8),自激气动力中的基波幅值比例均在95%以上。可以认为,试验所涉及的振幅和迎角,几乎不会影响自激气动力中线性成分所占比例。试验也表明,单自由度竖向振动,α=0°时,竖向振幅Av≤23mm(约化振幅Av/D=0.46) 的条件下,气动力中基本未发现明显高次谐波分量,基波幅值在气动力中占有的比例接近100%。
|
| 图 7 单自由度竖向振动中自激气动力频谱分析 Fig.7 Frequency spectrum of motion-induced aerodynamic force in single-freedom vertical vibration |
|
| 图 8 单自由度竖向振动中模型自激气动力基波幅值比例 Fig.8 First harmonic amplitude proportion of motion-induced aerodynamic force in single-freedom vertical vibration 注:“黑色阴影”代表升力,“斜划线”代表力矩 |
自激气动力的非线性高阶项对断面的运动状态或运动稳定都会有较大的影响[16],在进行非线性振动分析时不能随意简化,否则可能引起较大的误差。本文采用非线性最小二乘法对试验自激气动力信号进行拟合,并将拟合结果与原始信号进行比较,进而判断自激气动力非线性高阶项取舍的合理性。
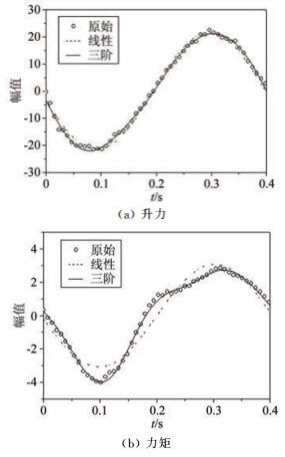
图 9为单自由度扭转振动、风迎角α=5°、振幅At=10°模型自激气动力拟合图,可以看出线性拟合与原始值有较大差别,而自激气动力的前3阶拟合数据和原始数据拟合基本重合。因此,对于流线型箱梁而言,对于高阶谐波幅值比例在5%以上的自激气动力,采用前3阶谐波进行拟合已经具有足够的精度。
|
| 图 9 单自由度振动中自激气动力曲线拟合 Fig.9 Fitting curve of motion-induced aerodynamic force in single-freedom torsional vibration |
以模型作单自由度竖向振动为例,自激气动力可以表示为:
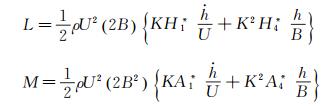 (2)
(2)
式中:ρ为空气密度;B为断面顺风向尺寸;K为折算频率,K=ωB/U,ω为振动圆频率。
由强迫振动装置的测量系统采集的同步位移数据,可获得相应的速度数据。根据线性自激气动力在不同时刻对应的位移值和速度值,可利用最小二乘法识别出断面的8个颤振导数。
图 10为单自由度振动不同振幅对应的颤振导数曲线图。从图中可以看出,单自由度扭转振动时,振幅的不同,颤振导数存在一定的波动:A2*随着振幅的增大而增大(气动阻尼减小),幅度接近20%,但没有快速接近0,这表明流线型箱梁断面在大振幅下的气动特性趋向钝体断面(A2*恒为正);A3*起初随振幅的增大而增大,在扭转振幅超过10°时,基本趋于稳定;H2*随扭转振幅增大波动幅度较大,接近30%;H3*基本不受扭转振幅的影响。单自由度竖向振动时,A1*、A4*、H1*基本不受竖向振幅的影响,但是H4*对竖向振幅相对敏感。图 10中的结果进一步表明,单自由度的扭转振幅仅影响非耦合的气动阻尼和气动刚度项,对于耦合项影响不明显;而试验范围内的竖向振幅则对相应的颤振导数值不产生实质影响。
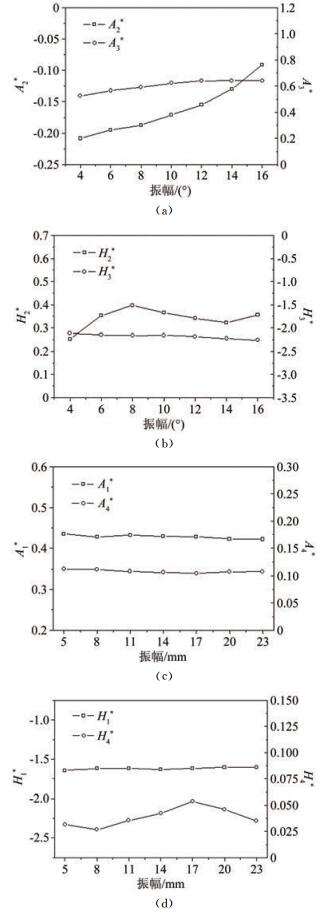
|
| 图 10 单自由度振动中不同振幅对应的颤振导数 Fig.10 Amplitude vs flutter derivative in single-freedom vibration |
结合强迫振动测压试验,对流线型箱梁断面自激气动力的影响因素进行了详细研究,主要结论如下:
(1) 当模型振幅处于“线性振幅”(扭转振幅≤8°,坚向约化振幅≤0.46) 范围时,自激气动力中基波幅值比例大致为95%,符合Scanlan的自激气动力线性假定。
(2) 对于流线型箱梁而言,单自由度扭转振动试验表明,大迎角、大振幅下,自激气动力的非线性特性显著。当自激气动力高阶谐波幅值比例较大时,采用前3阶谐波分量进行拟合能够满足精度要求。
(3) 单自由度扭转振动振幅对A2*、A3*、H2*均存在一定的影响,其中对A2*影响最大,而H3*基本不受扭转振幅的影响;单自由度竖向振动振幅仅对H4*有一定的影响。
需要指出的是,本文中的试验模型为没有栏杆等附属构件的裸梁断面。考虑栏杆后流线型断面的气动力特性将在后续研究工作中开展。
| [1] | Scanlan R H, Tomko J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, ASCE, 1971, 97(6): 1717–1737. |
| [2] | Bocciolone M, Cheli F, Curami A, et al. Wind measurements on the humber bridge and numerical simulations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41-44: 165–173. |
| [3] | Falco M, Curami A, Zasso A. Nonlinear effects in sectional model aeroelastic parameters identification[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41-44: 1321–1332. |
| [4] | Diana G, Resta F, Zasso A, et al. Forced motion and free motion aeroelastic tests on a new concept dynamometric section model of the messina suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92: 441–462. DOI:10.1016/j.jweia.2004.01.005 |
| [5] | Diana G, Resta F, Rocchi D. A new numerical approach to reproduce bridge aerodynamic non-linearities in time domain[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 1871–1884. DOI:10.1016/j.jweia.2008.02.052 |
| [6] | Diana G, Rocchi D, Argentini T, et al. Aerodynamic instability of a bridge deck section model: Linear and nonlinear approach to force modeling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98: 363–374. DOI:10.1016/j.jweia.2010.01.003 |
| [7] | Diana G, Rocchi D, Argentini T. An experimental validation of a band superposition model of the aerodynamic forces acting on multi-box deck sections[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 113: 40–58. DOI:10.1016/j.jweia.2012.12.005 |
| [8] | 陈政清, 于向东. 大跨桥梁颤振自激力的强迫振动法研究[J]. 土木工程学报, 2002, 35(5): 34–41. Chen Z Q, Yu X D. A new method for measuring flutter self-excited forces of long-span bridges[J]. China Civil Engineering Journal, 2002, 35(5): 34–41. |
| [9] | Liao H L, Wang Q, Li M S, et al. Aerodynamic hysteresis effects of thin airfoil and streamline box girder under large amplitude oscillation[C]//Proceedings of the ICWE 13, Amsterdam: Multi-Science Publishing Co Ltd, 2011. |
| [10] | 王骑, 廖海黎, 李明水, 等. 桥梁断面非线性自激气动力经验模型[J]. 西南交通大学学报, 2013, 48(2): 271–277. Wang Q, Liao H L, Li M S, et al. Empirical mathematical model for nonlinear motion-induced aerodynamic force of bridge girder[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 271–277. |
| [11] | Matsunmoto M, Shiraishi N, Shirato H, et al. Aerodynamic derivatives of coupled/hybrid flutter of fundamental structural sections[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49: 575–584. DOI:10.1016/0167-6105(93)90051-O |
| [12] | Noda M, Utsunomiya H, Nagao F, et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 101–111. DOI:10.1016/S0167-6105(02)00338-0 |
| [13] | Kareem A, Wu T. Wind induced effects on bluff bodies in turbulent flows: nonstationary, non-Gaussian and nonlinear features[C]. The 7th International Colloquium on Bluff-Body Aerodynamics and Its Application (BBAAVII Keynote), Shanghai, 2012. |
| [14] | 李文涛. 架设方法对大跨度悬索桥施工阶段颤振稳定性影响研究[D]. 成都: 西南交通大学, 2010. Li W T. Study on the influence of construction methods on flutter instability of long span suspension bridges under erection[D]. Chengdu: Southwest Jiaotong University, 2010. |
| [15] | 王骑, 廖海黎, 李明水, 等. 大振幅下薄翼和流线型箱梁的气动迟滞研究[J]. 实验流体力学, 2013, 27(1): 32–37. Wang Q, Liao H L, Li M S, et al. Aerodynamic hysteresis of thin airfoil and streamline box girder under large amplitude oscillation[J]. Journal of Experiment in Fluid Mechanics, 2013, 27(1): 32–37. |
| [16] | 王骑, 廖海黎, 李明水, 等. 大跨度桥梁颤振后稳定性[J]. 西南交通大学学报, 2013, 48(6): 983–988. Wang Q, Liao H L, Li M S, et al. Aerodynamic stability of long-span bridges in post flutter[J]. Journal of Southwest Jiaotong University, 2013, 48(6): 983–988. |



