2. 中国电子科技集团公司第二十一研究所, 上海 200233
2. The 21 th Research Institute of China Electronics Technology Group Corporation, Shanghai 200233, China
临近空间是指距地面20~100km高度之间的空间范围。临近空间介于常规航空器的最高飞行高度和航天器的最低轨道高度之间,是跨接航空与航天的新兴领域。在早期的航空航天飞行器研究中,对临近空间飞行器的军事和民用价值认识不足,随着科学技术的迅猛发展,人类对临近空间的认识逐步深化,其特有的应用价值和战略意义日益凸显,目前已是各航天航空大国关注的焦点[1-3]。
临近空间低速飞行器是指能够在临近空间区域飞行并执行特定任务的低速飞行器,主要包括高空气球、平流层飞艇、高空长航时无人机等,可广泛应用于侦察监视、通信中继、区域导航、环境监测、应急救灾和科学探测等领域[3]。与传统低空飞机相比,临近空间飞行器具有驻空时间长,侦查/通信覆盖范围广、载荷量大、隐身性能好、生存能力强等优点;与卫星相比,临近空间飞行器具有制造成本低、通信/侦查覆盖区域灵活、发射过程简单、可重复使用等诸多优点[4-6]。
临近空间低速飞行器在工作期间有姿态保持、位置机动、巡航跟踪和二次平台稳定等几种飞行控制模式。为保持控制鲁棒性、实现放飞和返回控制、高精度姿态和位置保持控制、姿态和位置机动控制,需要获取飞行时的风速信息[7]。因此,开展临近空间低速飞行器风速测量技术研究,对于飞行器飞行控制系统设计极为重要。但是截止目前,临近空间低速飞行器的风速测量一直是飞行器研究中的难点之一。这是因为在20km处的临近空间,大气静压仅为地面大气压的1/20,环境温度为-60℃左右。此外,临近空间低速飞行器的飞行速度较低,通常小于30m/s,飞行时来流动压约为5~40Pa,常规飞机上使用的风速管无法在如此低的动压下工作,而其他风速仪,诸如热线式风速仪、超声波风速仪均存在大气密度低导致测量精度差等问题。目前,临近空间低速飞行器的飞行试验是通过提前放飞探空气球测量高空风场,飞行试验时假定高空风场不变,以探空气球测量风速近似试验风速,或采用试飞场往年风场资料估计试验时的风速[8-9],上述方法无法获得飞行时的实时风速,可能存在较大的误差。
基于对临近空间低速飞行器的飞行速度测量的迫切需求,研究团队设计了一套旋转增压式风速仪系统,其特点是通过旋转旋杆,增加两端测压探头动压的原理,显著提高测量到的来流动压信号,从而有效提高风速的测量精度。系统搭载在临近空间低速飞行器上后,可实现飞行试验风速的实时测量。
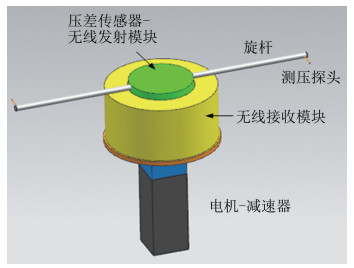
1 旋转增压式风速仪原理旋转增压式风速仪系统示意图如图 1所示,系统主要由电机、减速器组成的动力装置,压差传感器、无线通讯系统组构成的压差采集-发射-接收装置,以及旋杆、测压探头组成的流场感应装置构成。
|
| 图 1 旋转增压式风速仪三维示意图 Fig.1 3-D model of rotation anemometer |
如图 1所示,无线信号接收模块与电机-减速器外壳固联;压差传感器和无线信号发射模块安装于电机减速器转子上,随转子转动;旋杆穿过无线信号发射模块外壳,并采用螺钉紧固的方式与外壳固联。系统工作时,在电机-减速器带动下,旋杆与压差传感器-无线信号发射模块以恒定转速在水平面旋转,并通过旋杆两端压力探头实时测量当地的动压。其旋转增压测风速的原理如下所述。
当旋杆以恒定旋转角速率ω转动时,旋杆两端的测压探头相对转轴的线速度V为:
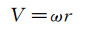 (1)
(1)
式中:r为旋杆的旋转半径。
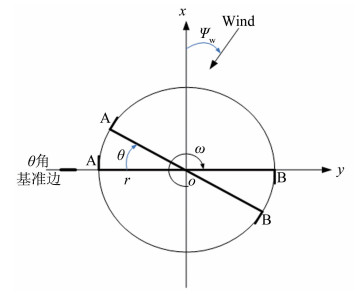
当刚性旋杆的转角与方位角的位置如图 2所示时,测压探头A和测压探头B相对于来流的速度VA和VB分别为:
|
| 图 2 风速仪风速测量原理图 Fig.2 Sketch of the wind speed measuring theory |
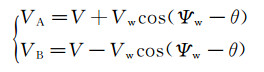 (2)
(2)
式 (2) 中,Vw为风速,Ψw为来流的风向角,θ为旋杆相对于基准位置的转角。此时,在A、B处的气流动压QA和QB分别为:
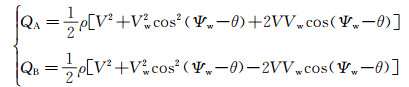 (3)
(3)
式中:ρ是来流密度。
此时,A、B处的动压差为:
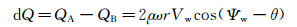 (4)
(4)
由式 (4) 可知,旋杆两端A、B的动压差为一周期性正/余弦信号。该信号的幅值与风速大小成正比。通过该式,可从压差信号中提取出风速信息,风速的解算式如式 (5) 所示。
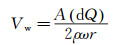 (5)
(5)
式中:A(dQ)表示压差信号的幅值。上式表明,当大气密度ρ、旋杆转速和长度不变时,来流速度与压差幅值成正比,其理论比值为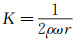
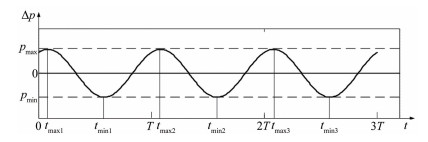
压差信号的理论仿真曲线如图 3所示,在多个周期内对测量曲线进行正/余弦函数拟合,可获得压差幅值,进而获得风速。
|
| 图 3 压差信号随时间变化仿真曲线 Fig.3 Simulation curve of the differential dependent on time dynamic pressure |
试验在中国电子集团公司第二十一研究所 (中电21所) 低温低压风洞中完成[10-11]。该风洞可模拟0~30km高空的大气压力;压力数值从室压 (101kPa) 到4kPa。当气压≥40kPa时,气压偏差≤±2kPa;当气压为4~40kPa时,气压偏差≤±5%。模拟温度范围:-70~85℃;温度波动度 (空载/常压下测试):≤±1℃;温度均匀性 (空载/常压下测试):≤±2℃;温度偏差 (空载/常压下测试):≤±2℃。

|
| 图 4 低温低压风洞 Fig.4 The near-space-environment wind tunnel |
内部设有的试验测试风道,气压为4~10kPa时 (对应10~30km高空),可以实现模拟0~30m/s的风速,对应不同温度,有标定理论风速。
2.2 旋转增压式风速仪图 5为风速仪在中电21所的低温低压风洞中的照片,风速仪由旋杆、信号发射模块、信号接收模块和伺服电机组成。

|
| 图 5 风速仪试验现场照片 Fig.5 Picture of rotation anemometer in test section of the wind tunnel |

|
| 图 6 旋杆与信号发射模块内部连接图 Fig.6 Inner structure of the rotation anemometer |
旋杆为系统的传压通道,同时通过旋转增加旋杆两端测量到的压差值,旋杆两端在旋转平面的迎风方向分别安装有2个测压探头;信号发射模块中安装有压差传感器、光电传感器和信号发射芯片,压差传感器的测压头通过软管与旋杆的连接接头相连,形成完整的传压通路;信号接收模块接收来自信号发射模块的压差和光电传感器信号。此外,旋杆和信号发射模块通过顶丝固连,并一起安装于电机转轴上,随转轴一起转动。
风速仪旋杆长度为0.6m,直径为8mm;测压孔直径为1.5mm,为了降低旋杆扰流对测压孔的流场干扰,测压探头的长度设计为大于旋杆直径的3倍,为30mm。
系统工作时,电机带动旋杆和信号发射模块在来流平面内转动,通过压差传感器测量旋杆两端测压探头的动压差,之后,信号发射模块采用射频传输的方式将动压差信号发送给信号接收模块,随后通过信号电缆将压差信号传输给上位机。
3 试验结果及分析 3.1 压差数据处理在近似临近空间环境 (大气温度为-60℃、大气静压为7kPa) 的状态下开展了风速仪的风速测量试验,试验风速范围为5~14m/s。此外,为了验证风速仪的相对测量精度,分别在大气温度为10和-60℃时开展了风速仪旋杆转速为600和500r/min的风速测量试验。
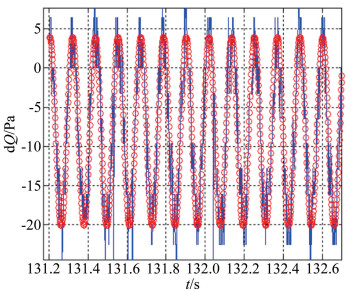
|
| 图 7 压差测量数据与正弦/余弦拟合结果对比图 (来流温度10℃,旋杆转速500r/min,理论风速10.36m/s) Fig.7 Comparison of measurements and sine fit results (with inflow temperature of 10℃, pressure-measuring arms rotating rates of 500r/min, and wind speed of 10.36m/s) |
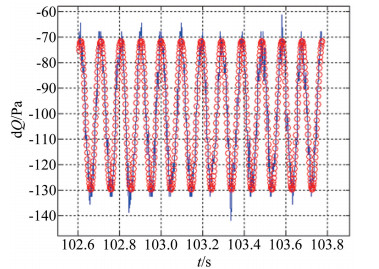
|
| 图 8 压差测量数据与正弦/余弦拟合结果对比图 (来流温度-60℃,旋杆转速600r/min,理论风速8.7 m/s) Fig.8 Comparison of measurements and sine fit results (with inflow temperature of-60℃, pressure-measuring arms rotating rates of 600r/min, and wind speed of 8.7m/s) |
由压差数据的正弦/余弦拟合结果可得如下结论:
(1) 正弦/余弦拟合结果与测量值拟合度很高,说明压差测量数据满足正弦/余弦规律,符合第1节中的理论分析和仿真结果。
(2) 此外,可以看到多个周期内压差幅值波动较小,说明测量数据比较稳定,测量误差被控制在较合理的范围内,试验结果可信度较高。
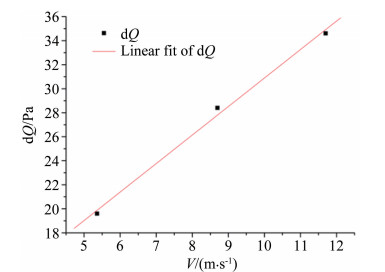
3.2 压差幅值与风速线性相关性分析对多个风速下的压差测量数据分别进行正弦/余弦拟合,获得不同风速下的压差幅值dQ。以理论风速为横坐标,压差幅值为纵坐标,可进一步获得理论风速-压差幅值关系曲线。当来流温度-60℃、来流静压为7kPa、旋杆转速600r/min时的理论风速-压差幅值关系曲线如图 9所示。
|
| 图 9 理论风速-压差幅值测量值及线性拟合曲线 (来流温度-60℃,旋杆转速600r/min) Fig.9 Amplitude of differential dynamic pressure data and linear fit results from wind speed (with inflow temperature of-60℃, and pressure-measuring arms rotating rates of 600r/min) |
由理论风速-压差曲线可知,dQ和V呈线性关系,符合公式 (5) 的分析结果,即:当外界大气密度恒定 (温度、压力不变)、旋杆转速恒定时,风速仪测量压差的幅值与来流速度成正比,可拟合为如下线性曲线:
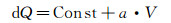 (6)
(6)
式中:Const为拟合的常数项,其物理意义是风速仪的压差传感器的测量误差;a为风速-压差幅值线性关系斜率。不同温度、不同旋杆转速下的风速-压差幅值线性拟合结果如表 1所示。
| 来流 温度/℃ |
理论风速 /(m·s-1) |
旋杆转速 /(r·min-1) |
斜率 a |
斜率 比 |
转速比 |
| 10 | 6.3、10.4、13.8 | 600 | 1.1261 | 1.184 | 1.2 |
| 500 | 0.9513 | ||||
| -60 | 5.4、8.7、11.6 | 600 | 2.3710 | 1.209 | 1.2 |
| 500 | 1.9596 |
由上表可知,拟合斜率比与旋杆转速比误差小于1.5%,可近似认为:
斜率比≈旋杆转速比
该结果与理论分析结果相同,即相同风速下,斜率比与旋杆转速成正比。此结论表明,风速仪压差测量的相对量可信度较高。
3.3 风速测量模型由上一节分析结果可知,风速仪的压差相对测量量符合理论分析结果,可信度较高。因此,可采用测量压差幅值与理论风速来标定当前的风速仪,获得风速仪在临近空间环境下的风速测量模型。
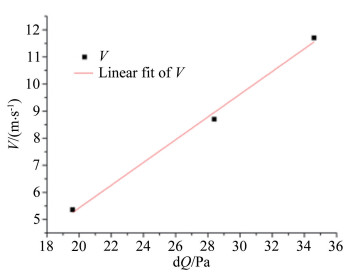
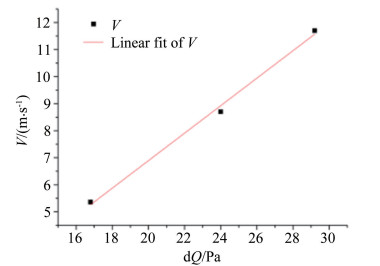
来流温度为-60℃、压力为7kPa时,不同旋杆转速下的风速仪标定曲线如图 10和11所示。
|
| 图 10 旋杆转速600r/min时的风速仪标定曲线 (来流温度-60℃,静压7kPa) Fig.10 Calibration curve of anemometer at rotation rate of 600r/min (with inflow temperature of-60℃, and static pressure of 7kPa) |
|
| 图 11 旋杆转速500r/min时的风速仪标定曲线 (来流温度-60℃,静压7kPa) Fig.11 Calibration curve of anemometer at rotation rate of 500r/min (with inflow temperature of-60℃, and static pressure of 7kPa) |
标定系数及标定误差如表 2所示。由标定系数可得,在临近空间环境下,旋转增压式风速仪的测量模型为:
| 风速标定表 | |||
| 转速600r/min | Pearson相关性系数 | 0.997 | |
| 数值 | 标准差 | ||
| 常数项 | -2.97107 | 0.81596 | |
| 斜率 | 0.41977 | 0.02892 | |
| 转速500r/min | Pearson相关性系数 | 0.998 | |
| 数值 | 标准差 | ||
| 常数项 | -3.27498 | 0.75244 | |
| 斜率 | 0.50836 | 0.03151 | |
旋杆转速:600r/min
V=-2.971+0.4198·dQ
旋杆转速:500r/min
V=-3.275+0.5084·dQ
4 结论本文开展了一种新型的旋转增压式风速仪的低温低压风洞风速测量试验,试验结果表明:
(1) 压差的测量值与正弦/余弦拟合结果一致性很高,说明压差测量数据满足正弦/余弦规律,符合理论分析结果;(2) 压差幅值波动较小,说明测量数据比较稳定,测量误差被控制在较合理的范围内,试验结果可信度较高;(3) 相同来流风速下,压差幅值与旋杆转速成正比,表明风速仪测量压差的相对量可信度较高;(4) 获得了风速仪在临近空间环境下、不同转速时的标定模型。
通过本文的研究,成功验证了当来流在风速仪旋转平面内时风速仪的测量能力,下一步研究重点是来流与风速仪旋转平面存在一定夹角时的风速测量模型。此外,如何精确测量风向角是目前尚未解决的难题。
| [1] | Young M, Keith L S, Pancotti A. An overview of advanced concepts for nearspace systems[C]//Proceedings of AIAA Joint Propulsion Conference and Exhibit, Colorado, USA, 2009. |
| [2] | Kurkcu C, Erhan H, Umut S. Unmanned aerial systems' near space operation concept[C]//Proceedings of 5th International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 2011. |
| [3] | 杨跃能. 平流层飞艇动力学建模与控制方法研究[D]. 长沙: 国防科学技术大学, 2013. Yang Y N. Dynamics modeling and flight control for a stratospheric airship[D]. Changsha:National University of Defense Technology, 2013. |
| [4] | 刘刚, 张玉军. 平流层飞艇定点驻留控制分析与仿真[J]. 自动控制与测量, 2008, 27(12): 64–66. Liu G, Zhang Y J. Analysis and simulation of stratospheric airship's fixed-point resident control[J]. Automatic Measurement and Control, 2008, 27(12): 64–66. |
| [5] | 李峰, 叶正寅. 平流层飞艇空气动力学研究进展[J]. 华东交通大学学报, 2008, 25(1): 24–27. Li F, Ye Z Y. Advances in aerodynamics research of stratospheric airship[J]. Journal of East China Jiaotong University, 2008, 25(1): 24–27. |
| [6] | 胡国昌, 吴美平. 平流层飞艇运动分析与仿真[J]. 哈尔滨工程大学学报, 2011, 32(11): 1501–1508. He G C, Wu M P. Motion analysis and simulation of a strotospheric airship[J]. Journal of Harbin Engineering University, 2011, 32(11): 1501–1508. DOI:10.3969/j.issn.1006-7043.2011.11.019 |
| [7] | 杨乐天, 张石玉, 张卫民. 高空驻空飞行器空速测量研究[C]. 第三届高分辨率对地观测学术年会, 2014: 284-290. Yang L T, Zhang S Y, Zhang W M. Research of anemometer applied in near space aircraft[C]. The 3rd China High Resolution Earth Observation Conference, 2014:284-290. |
| [8] | 张成. 临近空间大气认知建模及无人机飞行仿真[D]. 上海: 上海交通大学, 2008. Zhang C. The cognition and modeling of near space atmosphere and unmanned air vehicle flight simulation in variable wind field[D]. Shanghai:Shanghai Jiao Tong University, 2008. |
| [9] | 苗景刚, 周江华, 杨新. 基于Matlab/Simulink的飞艇全数字仿真系统[J]. 系统仿真学报, 2009, 21(9): 2658–2661. Miao J G, Zhou J H, Yang X. Airship digital simulation system based on Matlab/Simulink[J]. Journal of System Simulation, 2009, 21(9): 2658–2661. |
| [10] | 殷文华, 柳建华, 张良, 等. 模拟平流层环境的加载试验风洞测试与控制系统设计[J]. 航天器环境工程, 2015, 21(1): 49–52. |
| [11] | 张东宁, 王洪武, 赛庆毅, 等. 电机用平流层环境模拟实验装置[C]. 第二届高分辨率对地观测学术年会, 2013. Zhang D N, Wang H W, Sai Q Y, et al. An equipment for test motors used in stratosphere[C]. The 2nd China High Resoluation Earth Observation Conference, 2013. |



