流体壁面剪应力的精确测量是流体力学领域的难题[1]。随着MEMS技术的发展,硅基[2-3]和柔性聚合物基[4]的壁面剪应力微传感器研究发展受到重视,而传感器标定是其测量的基础和前提。根据不同应用需求初步形成了不同类型的动、静态壁面剪应力标定方法和装置[5-9]。本文介绍了平板流动、管道流动和旋转流动等静态标定方法,以及平面波振动、阶梯圆盘旋转运动等动态标定方法,介绍了工作原理和典型结构装置,可为壁面剪应力传感器标定方法的选定提供参考。
1 壁面剪应力静态标定方法壁面剪应力传感器的静态标定需要施加稳定已知量值的剪应力,读取对应输出。采用流体力学经典模型,通过测量其他物理量从而换算得到对应壁面剪应力值是常用方法。由于之前长期缺乏有效的流体壁面剪应力传感器,相关标定研究不系统,尚未形成统一的标准[10-11]。
目前,常见标定方法主要有平板模型标定法、管道流动标定法[12]和旋转运动标定法[13]。
1.1 平板模型标定法早在20世纪上叶就有学者和机构对平板模型边界层进行了大量理论和实验研究,并得到平板表面层流和湍流边界层壁面剪应力的理论计算模型。
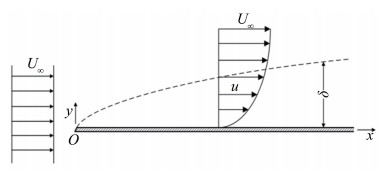
在空气中,均匀来流绕过一个厚度很薄的平板时,如果平板迎角为0,可以应用普朗特边界层微分方程解决粘性流动问题,平板边界层如图 1所示[14]。
|
| 图 1 平板边界层 Fig.1 The boundary layer along a flat plate |
理论上,由于平板绕流压强顺流不变,即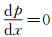
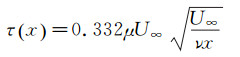 (1)
(1)
式中:μ表示流体的动力粘度,ν表示流体的运动粘度,U∞表示平板前端均匀来流流速,x表示距平板前缘的距离。
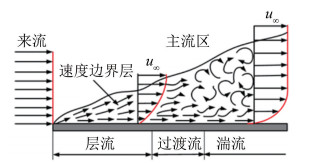
随着来流速度增大,雷诺数也将增大。当平板表面雷诺数大于临界雷诺数,绕流场可能由层流状态转变为湍流[15],如图 2所示。
|
| 图 2 平板边界层转捩 Fig.2 Laminar-turbulent transition on a flat plate |
通过动量积分方程可以得到湍流边界层中壁面剪应力的计算公式:
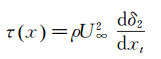 (2)
(2)
式中:xt为湍流边界层前沿到测量点的距离,ρ为空气密度,δ2为动量厚度,可通过下式计算得到:
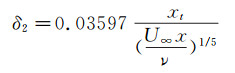 (3)
(3)
通过确定测量点到转捩位置的距离xt,就可以得到来流速度U∞与剪应力τ的函数关系。
由于平板表面发生转捩的位置不易测得,常常采用强制转捩的方法获得全湍流状态的平板边界层。Tani对转捩带粗糙体高度进行了研究,并得出粗糙体的极限高度计算公式[16]:
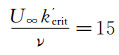 (4)
(4)
式中:k′ crit为粗糙体的极限高度。
平板模型标定法能产生数百帕量级的壁面剪应力,标定精度受风洞 (或水道) 来流速度测量误差、测试点距前缘距离测量误差及环境温度测量误差等因素的影响。然而,平板边界层的流场状态不易控制,可结合实验方法 (如升华法、油流法等) 初步判断平板表面流动转捩与分离情况。
1.2 管道流动标定法管道流动因其运动受到管壁约束,管道内的流动参数 (如流量、温度和壁面静压等) 较易测量,也是常见的剪应力标定方法。
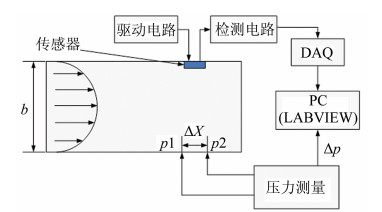
1.2.1 管道流动动量损失标定法当方形管道的宽高比较大时[17],入口处来流稳定的通道内流体运动可近似为二维流动。管道内流体的动量平衡与壁面剪应力作用相关[18]。通过测量管壁沿程压力损失,可以得到壁面剪应力的大小,标定装置如图 3所示。
|
| 图 3 动量损失剪应力传感器标定系统 Fig.3 The calibration system of wall shear stress sensors |
定义pinlet/poutlet为管道内入口处压力和出口处压力的比值。对于压力比pinlet/poutlet≤1.1,可忽略管道内流体的压缩性,完全发展的不可压缩层流管道内的压力分布是线性的,剪应力表达式可以简单表示为:
 (5)
(5)
式中:h为管道高度,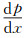
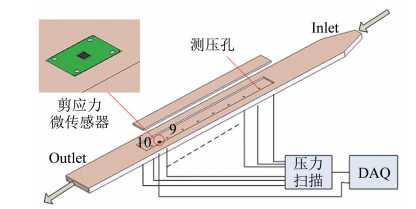
|
| 图 4 管道流动剪应力发生装置 Fig.4 Wall shear stress calibration device |
马赫数大于0.3的流动问题要考虑流体压缩性。对于压力比pinlet/poutlet≥1.1,管道内压力分布不再是线性变化[19]。通过非线性压力Π=p(x)/poutlet与非线性距离X之间的关系,代入公式 (5) 可以得到大压力比下的管道剪应力计算公式:
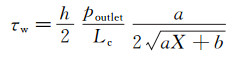 (6)
(6)
式中:Lc为管道的长度,poutlet为管道出口处的压力,X为沿管道方向x位置与管道长度Lc的比值。常数a和b能够从Π2=aX+b的曲线计算得到[20]。
1997年,美国麻省理工学院研发了一种基于动量损失原理的空气介质剪应力标定装置[21],量程0~1Pa,如图 5所示。在微型气槽内壁面开凿压力检测孔,由于流体在槽腔运动产生摩擦阻力引起流体动量的损失,导致沿气流运动方向有着不同的壁面压力分布,换算可得压差中点剪应力值。此外,还考虑了空气压缩性,给出了不同压差范围的剪应力计算方法并用此装置对自主研发的浮动元件式剪应力传感器进行了标定。
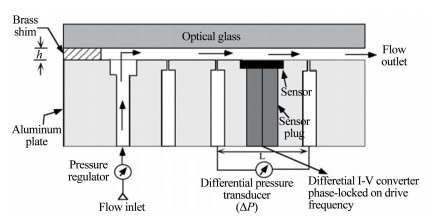
|
| 图 5 空气介质的剪应力标定装置示意图 Fig.5 Air static wall shear stress calibration device |
2002年,美国凯斯西储大学Patel等在研究壁面剪应力传感器时采用了此原理搭建起一套小型的扁平管道标定装置,并对浮动式剪应力传感器进行了标定,标定最大剪应力达到80Pa[18]。
2015年,中国空气动力研究与发展中心李建强等研究建立了管道流动动量损失原理的空气介质剪应力标定装置,增设了精密温控系统,可实现从环境温度到55℃的温度控制[22]。
2014年,中国船舶科学研究中心建立了水介质的动量损失管流标定装置,并利用LDV、PIV等对MEMS热膜剪应力传感器进行了测试标定[7]。
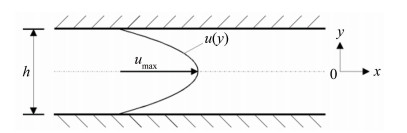
1.2.2 微型层流管道标定法流体在通过极低雷诺数的微型扁薄矩形水道 (具有较大宽高比w/h),可获得可控的槽内纯剪切流[23],如图 6所示。
|
| 图 6 扁形水槽内流体纯剪切流示意图 Fig.6 The boundary layer in a thin tunnel |
当管道内的流场形态为均匀层流时,其速度剖面曲线为二次曲线,管道体积流量Q与流动中心处最大流速相关,根据二维定常流动流体壁面剪应力的定义式[24],可以导出管道内壁面剪应力与体积流量之间的关系:
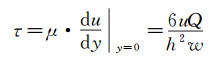 (7)
(7)
因矩形通道横截面宽度w无法实现远大于截面高度h,在剪应力计算时引入矩形通道的形状修正因子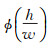
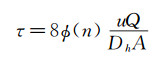 (8)
(8)
式中:Dh为水力学半径,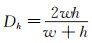
Φ(n) 为矩形通道的修正因子,该修正因子的引入可降低扁薄矩形水道侧壁对中心流速的影响效应[17],
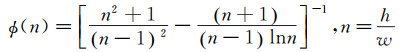 (9)
(9)
2005年,美国加州理工学院的Xu Y.等人根据该流动原理搭建起适用于MEMS剪应力传感器标定的微型管道测试平台,管道高度仅0.3mm,并实现对传感器0~5Pa范围内的剪应力标定[23]。
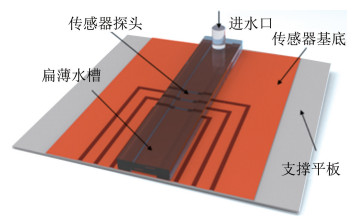
2009年,中国西北工业大学依此原理建立了微型扁薄标定水槽。2014年,李雁冰等根据该装置原理,对恒流驱动的热膜剪应力传感器进行了水下标定实验[25],并给出标定模型。王雷涛、严宇超等增加了溢流系统和温度控制系统,并对系统误差进行了分析。
|
| 图 7 微型扁薄水槽剪应力发生装置 Fig.7 The micro calibration tunnel of wall shear stress |
平板模型和管道流动标定装置均需要有气源或者水压动力源作为介质流动的动力,尤其搭建专门风洞较为困难,因此有研究者采用圆盘或者圆筒的旋转运动带动周边流场流动从而形成一定的壁面剪切应力。
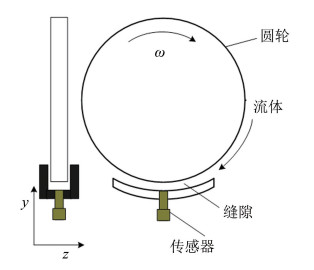
2004年,美国国家航空航天局 (NASA) Zuckerwar等采用旋转圆轮建立了标定装置[26],如图 8所示。1个电机速度可控的圆形旋转轮和1个与其同轴心的固定圆弧槽,传感器平齐安装在槽上且靠近轮的边缘。当旋转圆轮与传感器之间的间隙h极小时,圆轮与圆弧槽间的流体形成简单库艾特流动,产生的剪应力为:
|
| 图 8 旋转圆轮标定法示意图 Fig.8 Rotating wheel wall shear stress calibration device |
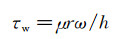 (10)
(10)
式中:r为轮子半径,ω为电机带动的旋转轮的转速,通过调节转速的大小可以获得需要的剪应力。
Zuckerwar通过对圆轮的精确安装,控制圆轮和同轴圆弧槽之间的缝隙最小达50μm,实现最大发生剪应力达到234.49Pa。
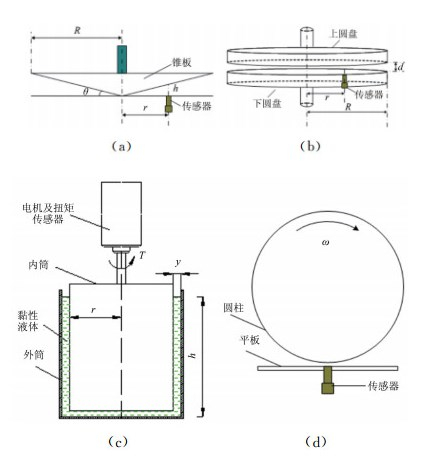
1992年,美国麻省理工学院的Shajii J[27]等采用锥板式[28-30]的剪应力标定装置对浮动式剪应力传感器标定进行过相关研究,如图 9(a)所示。2006年,韩国浦项科技大学机械工程系的Kim[31]等采用2个平行放置的圆盘建立了壁面剪应力标定装置,如图 9(b)所示,并对热膜剪应力传感器实现0~0.8Pa范围内的标定。另外,美国加州理工学院的Brown G. L.[32]等采用圆筒式粘度计[33-34]的构造,如图 9(c)所示,搭建了剪应力标定装置。2012年,日本名古屋大学的Terashima O.[35]等对圆筒剪应力发生装置进行了改进,将外圆筒改为平板,如图 9(d)所示,更便于传感器的安装。
|
| 图 9 (a) 锥板式标定装置原理图; (b) 静态标定的圆盘示意图; (c) 圆筒式旋转黏度计测量原理; (d) 旋转圆筒-平板标定法示意图 Fig.9 (a) Cone-plate wall shear stress calibration device. (b) Disk static calibration device.(c) Coaxial cylinder viscometers measurement device. (d) Rotating cylinder-plat wall shear stress calibration device |
旋转运动剪应力标定装置的搭建较为简单,但要保证产生剪应力的精度,对旋转装置偏心度要求较高,且若要产生较大范围的剪应力,圆盘或圆筒的直径和旋转速度要求很大。通常,此类方法仅用于0~2Pa范围内的剪应力标定。此外,该标定方法流场状态复杂,主要是利用其平均效应。
2 动态剪应力标定方法动态剪应力标定需要加载一个周期性变化的剪应力。通常动态标定是为了研究传感器在中频或者高频激励下的响应情况,因此需要动态标定装置能产生较高频率的激励信号。
2.1 平波管标定方法平波管实现动态测量原理为用扬声器产生声波,声波驱动流体产生动态剪应力信号,利用麦克风测量产生信号的频率实现对剪应力传感器的动态测量。管道尾部加入消声装置以消除回声对测量的影响。
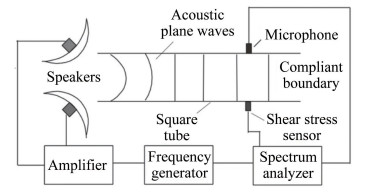
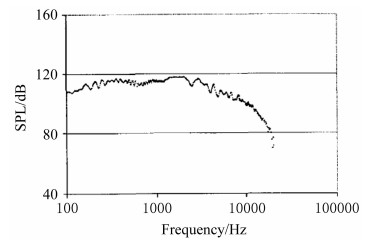
2000年,美国佛罗里达大学的Chandrasekaran等建立了以平面声波驱动的动态剪应力标定装置,如图 10所示,该装置可产生最大0.1Pa,频率范围100Hz到20kHz的动态剪应力信号,如图 11所示。利用该装置对带有隔热空腔的硅基热敏传感器进行了动态测试[9]。
|
| 图 10 佛罗里达大学动态标定装置示意图 Fig.10 Dynamic wall shear stress calibration device designed by university of Florida |
|
| 图 11 佛罗里达大学动态标定装置在恒定振幅激励下的频率响应 Fig.11 Plot of the frequency response of the PWT for constant voltage amplitude of speaker excitation |
2001年,美国麻省理工学院的Sheplak等采用相同原理的平波管动态标定装置,并对浮动式剪应力传感器动态性能进行了标定测试[11]。
平面声波将引起振荡的压力梯度,通过测量压力波动,可以换算得到壁面动态变化的剪应力[11]:
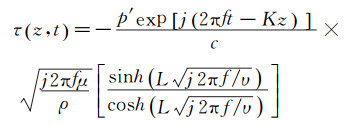 (11)
(11)
式中:p′为压力波动的幅值。
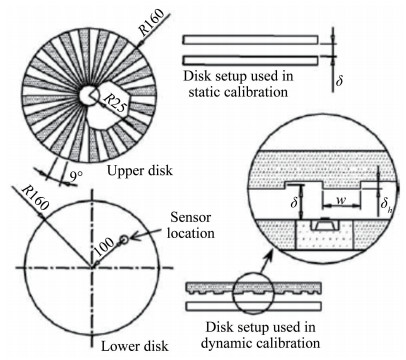
2.2 圆盘动态标定法2006年,韩国浦项科技大学机械工程系的Kim等在研究静态圆盘旋转标定法的同时对转动圆盘进行了改造,采用阶梯式转动圆盘,得到最高激励频率400Hz动态变化的剪应力,其结构如图 12所示。阶梯厚度为δh,2个圆盘的间隙的改变为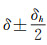
|
| 图 12 动态标定圆盘示意图 Fig.12 Disk dynamic calibration device |
介绍了国内外流体壁面剪应力标定方法及其原理和装置。通过对比分析,可以得到以下几点启示:
(1) 采用平板模型标定方法可以依托现成风洞或者水道,可以获得较大发生范围的剪应力 (从0帕到上百帕),实验系统可以适配多种类型的剪应力传感器;
(2) 微型管道流槽标定是一种紧凑便捷的专用标定装置,截面尺寸及雷诺数很小,水槽高度经常在毫米级以下 (百微米量级)。发生的剪应力范围通常在10Pa以内;
(3) 动量损失剪应力标定装置也属于专用定制,使用比较方便,剪应力发生范围极大 (可达上百帕);
(4) 旋转运动标定方法的装置较易搭建,对机械装置及装配等精度要求较高,发生的剪应力范围较小,其流场状态复杂,主要取用平均效应;
(5) 动态标定方法中研究及使用较多的是平波管法。
综上,可根据各类流体壁面剪应力传感器的工作要求、尺寸、安装条件 (贴附面为平面或曲面、安装高度等) 和应用环境的不同,选用不同的标定方法或装置。
目前,不同标定方法流场状态及品质影响,误差和不确定度及精度分析等研究较少,尚需关注。
| [1] | Xu Y, Jiang F, Newbern S, et al. Flexible shear-stress sensor skin and its application to unmanned aerial vehicles[J]. Sensors & Actuators A:Physical, 2003, 105(3): 321–329. |
| [2] | Sells J, Chandrasekharan V, Meloy J, et al. Microfabricated silicon-on-Pyrex passive wireless wall shear stress sensor[J]. Sensors, 2011: 77–80. |
| [3] | Chandrasekharan V, Sells J, Meloy J, et al. A microscale di-fferential capacitive direct wall-shear-stress sensor[J]. Journal of Microelectromechanical Systems, 2011, 20(3): 622–635. DOI:10.1109/JMEMS.2011.2140356 |
| [4] | Ma B H, Ren J Z, Deng J J, et al. Flexible thermal sensor array on PI film substrate for underwater applications[C]. Micro Electro Mechanical Systems (MEMS), IEEE 23rd International Conference, 2010:679-682. |
| [5] | Osorio O D, Silin N. Wall shear stress hot film sensor for use in gases[J]. Journal of Physics:Conference Series. IOP Publishing, 2011, 296(1): 012002. |
| [6] | Xiang D, Yang Y, Xu Y, et al. MEMS-based shear-stress sensor for skin-friction measurements[C]. Instrumentation and Measurement Technology Conference (I2MTC), IEEE, 2010:656-661. |
| [7] | 黄欢, 孙海浪, 田于逵, 等. 水下MEMS壁面剪应力传感器标定方案仿真分析与实验验证[J]. 实验流体力学, 2016, 30(2): 79–83. Huang H, Sun H L, Tian Y K, et al. CFD analysis and experimental validation on the scheme of calibration for MEMS wall shear stress sensors array for underwater applications[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 79–83. |
| [8] | Zhe J, Modi V, Farmer K R. A microfabricated wall shear-stress sensor with capacitative sensing[J]. Journal of Microelectromechanical Systems, 2005, 14(1): 167–175. DOI:10.1109/JMEMS.2004.839001 |
| [9] | Chandrasekaran V, Cain A, Nishida T, et al. Dynamic calibration technique for thermal shear stress sensors with variable mean flow[C]. Aerospace Sciences Meeting and Exhibit, 2000:56-65. |
| [10] | Scott M. The need for a shear stress calibration standard[C]. 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, 2004:28. |
| [11] | Sheplak M, Padmanabhan A, Schmidt M A, et al. Dynamic calibration of a shear-stress sensor using stokes-layer excitation[J]. AIAA Journal, 2001, 39(5): 819–823. DOI:10.2514/2.1415 |
| [12] | Ng K Y, Shajii J, Schmidt M A. A liquid shear-stress sensor fabricated using wafer bonding technology[C]. International Conference on Solid-State Sensors and Actuators, 1991:931-934. |
| [13] | Hyman D, Pan T, Reshotko E, et al. Microfabricated shear stress sensors, part 2:testing and calibration[J]. AIAA Journal, 1999, 37(1): 73–78. DOI:10.2514/2.666 |
| [14] | 章梓雄, 董曾南. 粘性流体力学[M]. , 2011. Zhang Z X, Dong Z N. Viscous fluid mechanics[M]. Beijing: Tsinghua University Press, 2011. |
| [15] | Ludwig P. Applied hydro-and aeromechanics[M]. , 1957. |
| [16] | Tani I, Hama R, Mituisi S. On the permissible roughness in the laminar boundary layer[J]. Report of the Aeronautical Research Institute Tokyo Imperial University, 1940, 15: 417–428. |
| [17] | Schetz J A, Fuhs A E. Handbook of fluid dynamics and fluid machinery:fundamentals of fluid dynamics, Volume Ⅰ[J]. Journal of Fluids Engineering, 1996, 118(2): 218. DOI:10.1115/1.2817366 |
| [18] | Patel M P, Reshotko E, Hyman D. Microfabricated shear-stress sensors, part 3:reducing calibration uncertainty[J]. AIAA Journal, 2002, 40(8): 1582–1588. DOI:10.2514/2.1827 |
| [19] | Zucrow M J, Hoffman J D. Gas dynamics (vol1)[M]. , 1976. |
| [20] | Arkillic E B, Breuer K S. Gaseous flow in small channels[C]. AIAA, Shear Flow Conference, Orlando, FL, 1993. |
| [21] | Padmanabhan A, Goldberg H, Breuer K D, et al. A wafer-bonded floating-element shear stress microsensor with optical position sensing by photodiodes[J]. Journal of Microelectromechanical Systems, 1997, 5(4): 307–315. |
| [22] | Liang J M, Yang D G, Li J Q, et al. Calibration of a thermal MEMS shear stress sensor array[J]. Arabian Journal of Geosciences, 2015, 8(10): 8089–8105. DOI:10.1007/s12517-015-1781-z |
| [23] | Xu Y, Lin Q, Lin G, et al. Micromachined thermal shear-stress sensor for underwater applications[J]. Journal of Microelectromechanical Systems, 2005, 14(5): 1023–1030. DOI:10.1109/JMEMS.2005.856644 |
| [24] | Liu C, Huang J B, Zhu Z, et al. A micromachined flow shear-stress sensor based on thermal transfer principles[J]. Journal of Microelectromechanical Systems, 1999, 8(1): 90–99. DOI:10.1109/84.749408 |
| [25] | Li X Y, Li Y B, Ma B H, et al. Modelling and calibration of microthermal sensor for underwater wall shear stress measurement[J]. Micro & Nano Letters, 2014, 9(7): 486–489. |
| [26] | Zuckerwar A, Scott M. A rotary flow channel for shear stress sensor calibration[C]. 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2004:2303. |
| [27] | Shajii J, Ng K Y, Schmidt M A. A microfabricated floating-element shear stress sensor using wafer-bonding technology[J]. Journal of Microelectromechanical Systems, 1992, 1(2): 89–94. DOI:10.1109/84.157363 |
| [28] | 陈惠钊. 粘度测量[M]. 第二版. 北京: 中国计量出版社, 2002: 56-103 Chen H Z. Viscosity measurement[M]. 2nd ed. Beijing:China Metrology Press, 2002:56-103 |
| [29] | Bindzus W, Fayard G, Van Lengerich B, et al. Application of an in-line viscometer to determine the shear stress of plasticised wheat starch[J]. Starch-Stärke, 2002, 54(6): 243–251. DOI:10.1002/(ISSN)1521-379X |
| [30] | Buschmann M H, Dieterich P, Adams N A, et al. Analysis of flow in a cone-and-plate apparatus with respect to spatial and temporal effects on endothelial cells[J]. Biotechnology and Bioengineering, 2005, 89(5): 493–502. DOI:10.1002/(ISSN)1097-0290 |
| [31] | Kim I C, Sang J L. Characterization of a miniature thermal shear-stress sensor with backside connections[J]. Sensors & Actuators A:Physical, 2006, 128(2): 305–311. |
| [32] | Brown G L, Davey R F. The calibration of hot films for skin friction measurement[J]. Review of Scientific Instruments, 1971, 42(1): 1729–1731. |
| [33] | 肖文涛, 张国忠, 刘坤, 等. 同轴圆筒旋转粘度计测量误差的分析与修正[J]. 现代科学仪器, 2012(2): 114–118. Xiao W T, Zhang G Z, Liu K, et al. Analysis and correction for measurement errors of coaxial cylinder viscometers[J]. Modern Scientific Instruments, 2012(2): 114–118. |
| [34] | 谢尧生, 夏桂清. 旋转粘度计圆筒尺寸对粘度测试的影响[J]. 硅酸盐通报, 1984(1): 44–51. Xie Y S, Xia G Q. Rotational viscometer cylinder size effect on viscosity test[J]. Bulletin of the Chinese Ceramic Society, 1984(1): 44–51. |
| [35] | Terashima O, Sawada T, Sakai Y, et al. Measurement of wall shear stress by using micro-fabricated sensor[C]//Proceedings of ISEM, Japan, Nagoya University, 2012. |



