2. 先进航空发动机协同创新中心, 北京 100191
2. Collaborative Innovation Center of Advanced Aero-Engines, Beijing 100191, China
边界层转捩与飞行器的气动特性紧密关联,理解边界层转捩过程对飞行器设计具有重要意义。一般来说边界层转捩过程可以大致分为感受性、线性增长、非线性饱和、二次失稳和破碎等5个发展阶段[1]。这种理想化分法并不代表每个阶段都会在转捩过程中清晰地出现,但其为更好地理解复杂流动提供了一个很好的框架。根据不同的雷诺数、来流扰动、曲率和粗糙元等,不同的稳定性机制将单独或者综合地导致某一路径的转捩过程。按照Morkovin[2]提出的旁路转捩概念 (bypass),可以将转捩路径简单地分为传统转捩路径和旁路转捩路径。关于旁路转捩的文献很多,这里不赘述,感兴趣的读者可参见Durbin & Wu的综述[3]。传统的路径即T-S波路径。T-S波是指线性稳定性理论预测的边界层内的不稳定波,其最早由Tollmien和Schilichting先后对O-S方程的求解得到,并在1947年得到了Schubauer和Skramstad的实验验证。传统转捩的具体过程参见Kachanov[4]、Lee[5]等综述。
低速稳定性理论及转捩预测方法不能简单推广到高超声速情况。Mack[6]利用线性稳定性理论 (LST) 发现除了第一模态不稳定波外,当马赫数大于2.2时,还存在一族在声速线和壁面来回反射的声波,其中最不稳定的模态被称为Mack第二模态。Mack第一模态又被称为涡模态,类似不可压缩流动中的T-S波;而Mack第二模态波又被称为声模态,它在高超声速边界层转捩过程中扮演着十分重要的角色。Stetson等[7-11]在普通高超声速风洞中 (Ma8) 用热线较为系统地研究了7°半锥角的尖锥和钝锥的边界层稳定性,包括迎角、雷诺数、噪声和冷热壁面等影响,他们观察到了Mack第二模态,并认为其对转捩起主导作用。但这一结论并非普适规律。Bountin等[12]用热线实验研究了Ma6尖锥边界层扰动演化规律,发现在转捩过程中起决定作用的是Mack第一模态。相似结论的还有Dong和Luo[13]用数值模拟的方法研究Ma6尖锥边界层转捩,他们也发现在转捩中起主导作用的是Mack第一模态波。高超声速边界层破碎机制也和低速边界层破碎机制不尽相同。Pruett[14]通过DNS研究Ma8圆锥边界层转捩,发现一对Mack第二模态斜波可以非线性相互作用产生很强的流向涡和展向速度脉动,从而导致破碎。Fezer等[15]发现斜波破碎比亚谐破碎更有可能主导高超声速边界层破碎。然而,高超声速边界层转捩及破碎机制目前仍未被充分理解,尤其是不同模态之间的相互作用、转捩后期强非线性过程以及旁路转捩机制等。
不论是低速边界层还是高超声速边界层,上述工作是基于边界层内已有不稳定波的发展,均未回答边界层内不稳定波 (T-S波、Mack不稳定模态波等) 是如何产生的,即感受性问题。感受性指的是外界特定扰动进入边界层的方式及其在扰动流中的信号特征[16],从某种意义上讲感受性问题即边界层内不稳定波的起源和激发问题,它为层流最终破碎时的幅值、频率和相位等参数提供了重要的初始条件。与稳定性问题不同,感受性强调的是边界层对外界扰动的响应。外界扰动如湍流度不同,转捩的位置和机理也会不同,如何确定转捩与扰动之间的定量关系,是感受性研究需要解决的问题[17]。之所以至今仍未有预测转捩雷诺数的统一数学模型,除了对转捩非线性过程理解的局限性外,另一方面则是影响转捩的因素众多,如来流湍流度、声扰动、熵扰动、表面几何形状和粗糙元等,它们均与感受性问题紧密相关。根据扰动源的不同,可将感受性分为自由流扰动的感受性 (如声波、涡波以及熵波等) 和壁源扰动感受性 (如粗糙元、壁面振动、壁面吹吸以及壁面加热等)[18]。感受性作为边界层转捩预测和控制的关键,在不可压边界层中已被广泛地研究[19-20],早期对低速感受性研究一般致力于尺度转化问题,即外界扰动的特征长度如何发展成边界层内不稳定波的波长,可以参考Saric的综述[21]。
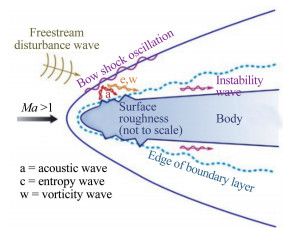
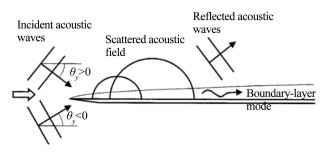
近几年在高超声速飞行器的研究热点下,国际上越来越意识到高超声速边界层感受性的重要,但相关工作大多限于理论和数值计算方面,具体可参见Zhong & Wang[22]、Fedorov[23]及Balacumar[24]的综述。高超声速流动中感受性问题如图 1所示。自由流中的声波、涡波和熵波等进入边界层前均需穿过激波,并和激波相互作用。不论什么形式的扰动波,它们和激波相互作用后均能产生上述3种波[25]。Ma & Zhong[26]考虑了在高超声速边界层研究中容易被忽略的因素即声波和斜激波的相互作用。他们发现在前缘附近激波和边界层之间存在强烈的声波反射,其能影响边界层感受性过程,同时该过程也偏离了McKenzie & Westphal的线性预测[25]。另外,由于边界层转捩控制往往通过壁面条件实现,因此壁源扰动的感受性也至关重要。
感受性研究的主要理论工具是渐近方法[27-28] (Asymptotic methods)、多模态法[29](Multiple-mode methods) 以及抛物化方程法[30](PSE) 等,这些方法计算代价较小,易于进行参数化研究来解释较为普遍的规律,但每种方法都采用了一些特定的假设条件,这些假设条件所带来的影响仍有待实验的检验。相对而言,直接数值模拟[22](DNS) 的假设较少,数据丰富,但是其计算代价较大,尤其是高雷诺数时,系统的研究工作还较少见。风洞实验对高超声速边界层感受性研究的必要性和重要性毋庸置疑,其不仅具有很强的工程意义,而且能够检验理论和计算的可靠性,甚至揭示新的机理。目前,关于高超声速边界层感受性实验的数据十分有限,主要是Maslov小组在2001年前后的研究[31]。导致实验困难的重要原因是实验条件的限制和测量手段的困难。普通高超声速风洞的噪声水平要比飞行器飞行环境的噪声高1到2个数量级[32],因而其并不能模拟实际飞行环境。而感受性研究需要严格的扰动控制,对于高超声速边界层来说,尤其需要控制噪声水平,避免风洞喷管壁面的湍流边界层产生的马赫波造成实验干扰,尽可能地维持喷管壁面为层流边界层。这就对风洞提出了苛刻的要求,即尽可能采用静风洞进行研究。然而,历经近50年的探索,静风洞实验仍未普及,其建造和调试不仅昂贵而且十分复杂,目前世界上也仅有4座真正意义上的静风洞 (美国普渡大学2006年调试成功,德克萨斯农工大学于2010年调试成功,另外2座不同喷管喉径的Ma6静风洞由北京大学于2013年先后调试成功,它们的噪声水平在1‰左右,比普通高超声速风洞低一个量级[33])。此外,高超声速边界层实验具有典型的“四高”特性 (高温、高压、高速、高频),高响应频率的热线容易被吹断使实验成本较高,而基于PIV技术的场测量手段因频率响应较低、近壁剪切应力大及粒子播撒困难而难以得到广泛应用,压力传感器因无法有效捕捉空间场信息,使得其系统测量受到限制。因而高超声速边界层的感受性实验研究依然十分匮乏,也亟待应用静风洞和新的实验技术开展系列实验。
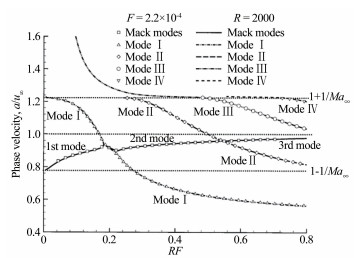
高超声速边界层中含不稳定模态 (Mack第一模态和Mack第二模态等) 和稳定模态 (Mode Ⅰ,Mode Ⅱ等),如图 2所示。其中Mack第二模态在实验中观察到的图像可参见最新的流动显示实验[34]。在感受性过程中,线性稳定模态在感受性问题中的地位不能忽略,它可以和扰动波及不稳定模态共振,从而将能量从扰动波传递到不稳定模态波。为了研究高超声速边界层感受性问题,Fedorov & Khokhlov[27-28, 35-36]分别采用了渐近方法和多模态法详细描述了扰动的动力学过程,并以此发展出了前缘感受性理论 (Leading-edge receptivity theory) 和模态转化理论 (Inter-modal exchange theory),奠定了其在该研究领域的重要地位。前缘感受性理论主要讨论前缘附近的声波衍射和散射过程,该理论与Maslov等人的部分实验结果[31]相吻合。而模态转化理论则结合了Ma & Zhong的DNS结果[37],是该领域理论研究的创新工作,详见其2001和2003年的文章[36, 38-39]。本文通过对目前高超声速边界层感受性的已有认识进行梳理,以期对开展该方向的实验研究有所启发和指导。
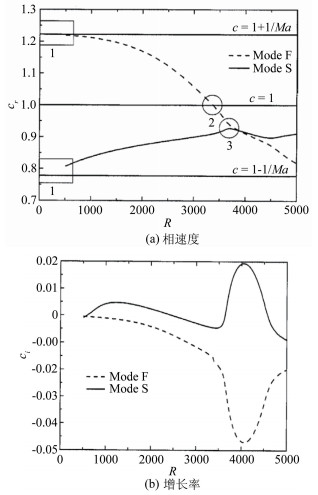
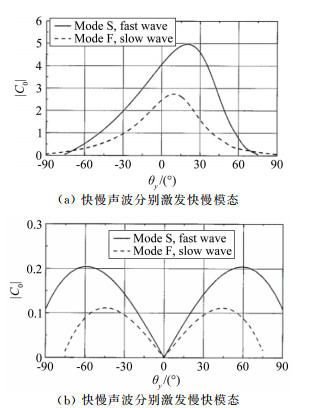
Fedorov & Khokhlov[38]提出在前缘附近存在2个边界层模态,分别为“Mode S”和“Mode F”(下文称“慢模态”和“快模态”)。慢模态是指在前缘处相速度趋向于慢声波的模态 (c→1-1/Ma);快模态是指在前缘相速度趋于快声波的模态 (c→1+1/Ma),如图 3(a)所示。快慢模态从前缘向下游发展过程中将经过3个区域 (见图 3(a)中的区域1、2和3)。在前缘区域1附近,快、慢模态分别与快、慢声波同步。快慢模态对声波的感受性通过耦合系数来表示,如图 4所示,快声波和慢声波分别能有效地激发快、慢模态 (见图 4(a)),同样,慢声波可以激发快模态、快声波也可以激发慢模态,但它们耦合系数比前者小很多,见图 4(b)。沿着下游发展,快模态的相速度达到熵波/涡波的相速度 (c=1),即区域2。由于非平行效应,快模态将和熵波/涡波相互作用。当快模态穿过cr=1时,理论上其相速度的虚部将有一个跳跃,其详细的扰动过程分析参见Fedorov 2001年和2003年文章[36, 39]。但该过程仍待实验验证。再往下游发展,快模态将与慢模态在区域3同步,然后其中一个模态将变成不稳定模态。在图 3(b)所示的情况下,慢模态的增长率为正,逐渐发展为Mack不稳定模态。在R=1000和4000附近有2个增长率最大值,它们分别代表Mack第一模态与Mack第二模态。
前缘声波感受性不论在可压缩还是不可压缩边界层中都得到了许多学者的关注。声波在遇到尖前缘时将会发生反射、衍射或者散射过程,如图 5所示。不同的入射角会有不同的主导过程。当θy=0时,由于此时散射可以忽略不计,衍射成了主要过程。当θy < 0时,散射和衍射同时影响扰动场,而θy>0时,还需要考虑反射声波对感受性过程的影响。Fedorov通过引入小参数ε=Δ1/2F1/4建立渐近结构来分析前缘感受性,其中Δ是位移厚度的度量,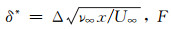
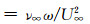
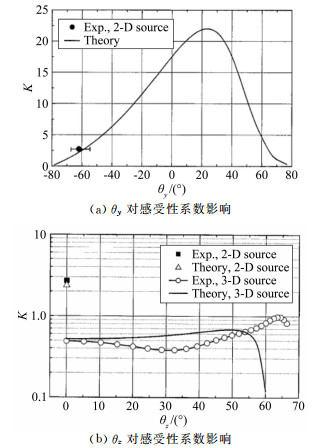
Maslov[31]利用辉光放电产生声波并通过测量流量幅值来获得感受性系数。图 6显示慢模态对声波角度变化的感受性系数的幅值演化,迎角θy的实验结果很好地吻合理论预测, 如图 6(a)所示。对于声波扫掠角在范围为0 < θz < 50°时,实验结果虽然也能大致符合理论结果,但当θz太大时,理论预测和实验相差较大,如图 6(b)所示。Fedorov解释[38]大扫掠角时实验与理论分歧较大的原因可能是实验数据不确定导致,另外他认为此时的扰动场改变了渐近结构,因此需要新的渐近结构 (他认为一种可能的渐近结构是三层结构理论)。在周恒的书中[41]指出这些具有较强三维性的Mack第一模态 (慢模态) 的激发机理与亚声速边界层类似,包括涡波/声波相互作用、声波/涡波与壁面粗糙元相互作用。
2 模态转化机制Ma & Zhong的DNS结果[37]显示在0°迎角时,快声波能够产生慢模态,这和Fedrov渐近理论模型的预测结果 (见图 4(b)) 不一致,表明离开前缘向下游发展过程中存在某种机制将能量传递到慢模态。Fedorov在2001年用模态转化机制来解释该现象[36]。根据之前介绍,快慢模态可以直接由快慢声波激发,也可以由前缘散射的声场激发。慢模态逐渐演变成Mack第一模态,并最终变成Mack第二模态,而快模态逐渐消减。但是Mack第二模态并非总是来源于慢模态,这还取决于快慢模态在前缘下游的同步过程。Fedorov采用多模态分析方法发现[36],快模态在感受性过程中的作用十分重要,其可能在同步点附近激发Mack第二模态,并实现快慢模态之间的能量传递。在同步点处,由于2个模态的相速度非常接近,使得它们很容易因基本流的弱非平行效应而相互作用,从而导致模态转化。吴雪松在周恒等专著中指出[41]一个模态在非平行流中传播时,其形状会偏离局部特征函数,由此产生的畸变在另一模态的特征函数上的投影一般不是零,这样的散射效应将一个模态的部分能量转化到另一个模态。Balakumar[24]通过数值计算发现涡波可以直接激发Mack第二模态,也能先激发快模态,通过快模态将能量转换至慢模态。其结果很好地证实了Fedorov关于模态转化的理论。另外,Fedorov & Khokhlov在2002年指出[18],在同步点附近,边界层对壁源扰动 (如壁面振动或者吹吸) 非常敏感。Ma & Zhong的DNS结果[42]也证实了快模态是近前缘的主要成分。
前缘感受性机制和模态转化机制谁成为主导机制,需要根据具体情况而定。扰动位置靠近前缘时,若扰动频率较高且由慢声波直接激发慢模态的情况时,前缘感受性更强,在较低扰动频率和绝热壁面时,慢声波的感受性是快声波的50~70倍。若慢模态主要由快声波通过模态转化机制激发的情况时,模态转化机制将起着主导作用,尤其是壁面温度足够低的时候,此时初始扰动点位置对感受性过程有较大影响。对于绝热壁面前缘感受性要强于模态转化机制,但对于冷却壁面情况相反[38],这是因为冷壁面能够抑制Mack第一模态 (慢模态),强化快慢模态的相互作用,此时初始扰动只有距同步点上游较远位置时才具有较强的感受性。最后需要指出的是,前缘感受性和模态转化机制之间的关系强烈依赖于同步点的位置,即与主流参数及扰动频率密切相关。
近来,Gao等[43]发现关于快慢声波感受性过程的新机制。他们指出快慢声波存在非线性相互作用,进而产生和频 (Sum-frequency) 扰动,从而激发Mack第二模态。
3 感受性的影响因素前文主要讨论了高超声速边界层对声波的感受性机制。下文将介绍影响感受性过程的主要因素。
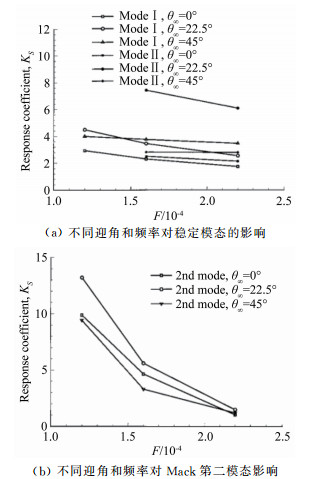
3.1 扰动频率的影响Ma & Zhong[26]采用DNS系统地研究了入射波的角度和频率对感受性的影响,他们发现Mode Ⅰ(含快模态) 和Mode Ⅱ对迎角变化十分敏感,但对频率变化不敏感;而Mack第二模态则相反,如图 7所示。
张玉东等[44]用激波装配法对钝锥的感受性计算表明随着扰动频率的减小, 边界层内Mack第一模态区范围变大,Mack第一模态的衰减和第二模态的增强向下游延迟;扰动的振幅随着扰动频率的减小逐渐增大,超过某一临界点后随着扰动频率的减小逐渐减小,这与最近Shi等[45]用DNS计算的结果类似。
3.2 几何形状的影响目前对高超声速边界层感受性研究的模型往往是圆锥、楔形体和平板等。其中圆锥又分为直锥、裙锥及其结合体。根据前缘钝度来分,又可以分为钝锥、尖锥等。Kara等[46]采用数值模拟的方法计算圆锥 (5°钝头) 和楔形体在高超声速边界层中的感受性,发现绝热壁面的情况下 (F=1.4×10-4),圆锥前缘对慢声波的感受性是快声波的67倍,因而他们认为慢模态比快模态更容易在高超声速边界层内激发出不稳定波。而楔形体对声波的感受性比圆锥要小5倍左右。Balakumar等[47]分别计算了直圆锥、裙锥以及它们的组合体对声扰动和涡扰动的感受性,并考虑了不同钝度的影响。通过与静风洞实验进行对比,他们发现裙锥因逆压梯度的存在将使Mack第二模态波的频率变高;圆锥前缘钝度增大能使Mack第一模态稳定,并降低前缘感受性;钝锥的感受性系数比尖锥要小近3个数量级。这是因为钝锥的前缘往往需要考虑熵层的影响,外界扰动进入边界层前需先进入熵层,从而降低了对声波的感受性。另外,张玉东等[44]发现钝度减小,边界层内不稳定波的扰动幅值增大,但存在一个临界值,超过临界值之后反而减小。但钝度较小的时候,虽然提高钝度能够延迟转捩,但是钝度超过一定值后又将使转捩提前,这就是所谓的“钝体悖论”[48],其原因仍待探索。
3.3 壁面温度的影响由于热防护对高超声速飞行器再入的重要性,很多学者研究了壁面温度对转捩的影响。
3.3.1 不同壁面条件的影响一直以来,壁面冷却对转捩的影响有不同的观点[49-50]。有的学者认为冷却壁面能够使转捩延迟,如图 8所示。但有的学者通过实验发现冷却壁面也能够使转捩提前[51-53]或者不影响[54],壁面对转捩及感受性的影响总结如表 1所示。
| 研究者 | 模型 | Ma | 方法 | 壁面条件 | 结论 |
| Fedrov et al.2003 | 平板 | 6 | 理论 | 绝热 | 感受性:慢声波/快声波≈50 |
| 冷壁 | 快模态可能失稳 | ||||
| Ma & Zhong2001 | 平板 | 4.5 | 计算 DNS |
绝热 | 等温比 绝热对声波的感受性小 |
| 等温 | |||||
| Balakumar2015 | 楔形圆锥 | 6 | 计算 | 绝热 | 感受性:慢声波/快声波≈20 |
| 冷却 | 冷却 (尖锥):转捩提前 | ||||
| Kara et al.2007,2008 | 楔形直锥 | 6 | 计算 | 绝热 | 感受性:慢声波/快声波≈67 |
| 冷却 | 冷却时转捩提前 | ||||
| Blanchard 1995 | 裙锥 | 6 | 实验 | 绝热/冷却 | 冷却时转捩提前 |
| Demetriades 1978 | 直锥 | 8 | 实验 | Tw: 0.41~0.8 | 冷却时转捩提前 |
| Lysenko & Maslov 1984 | 平板 | 2/4/6 | 实验 | Tw: 0.3~1 | 冷却对声波没影响Mack第一模态稳定第二模态失稳 |
| Stetson et al. 1989 | 直锥 | 8 | 实验 | Tw=0.42 | 冷却时转捩提前Mack第二模态频率变高,增长率变大 |
| Polivanov2011 | 平板 | 5.4 | 理论计算 | 冷却加热 | 冷却时转捩提前冷却位置影响转捩 |
| Sidorenko et al. 2015 | 直锥 | 6 | 实验计算 | 局部冷却 | 抑制第二模态转捩延迟 |
| 局部加热 | 与局部冷却结果相反 | ||||
| Soudakov et al.2009 | 平板 | 6 | 计算DNS | 温度跳跃 | 温度跳跃影响感受性 |
| Sanator et al. 1965 | 尖锥 | 8.8 | 实验 | Tw: 0.08~0.4 | 没有明显影响 |
| 注:Tw指壁面温度/绝热温度 | |||||
事实上,根据表 1中不同学者的研究发现,壁面温度对转捩的影响需要考虑转捩过程由谁主导 (Mack第一模态与第二模态的竞争)、冷却或加热的位置 (离前缘或同步点的位置) 与方式 (局部冷却或全局冷却) 等。关于感受性过程,由第一节可以知道,快、慢模态在区域3(见图 3) 附近相互作用,其中一个模态会将能量传递给另一个,并使其发展为Mack第二模态。这个模态转化过程就和壁面温度有关。一般绝热壁面[26, 31]情况下,慢模态失稳,发展为Mack不稳定模态;但对于冷却壁面的情况 (在一定频率下),则快模态失稳[38]。由于一般实验的壁面温度条件介于绝热和等温之间,所以Ma & Zhong[26]用直接数值模拟研究了绝热与等温2种特殊壁温条件对感受性的影响。他们发现一般在等温壁面条件时对快声波的感受性要比绝热条件下小 (θy=0, F=2.2×10-4),如图 9所示。另外,他们发现在等温壁面时,Mack第二模态的的幅值比绝热壁面要小得多。改变频率和迎角,上述结论同样成立。
Kara等[51]研究冷却壁面对感受性系数的影响,发现冷却壁面时,边界层对快声波感受性更强,对Mack第一模态有稳定作用,并且使转捩位置提前。同Kara的结果类似,Balakumar等[47]通过数值计算考虑了绝热壁面和冷却壁面对高超声速边界层感受性的影响。对于尖锥,冷却壁面时前缘对声波的感受性是绝热壁面时的1/100。冷却壁面使Mack第一模态趋于稳定,但使Mack第二模态变得更不稳定,该结果与线性稳定性理论预测及Demetriades[53]、Lysenko & Maslov[55]以及Blanchard[52]等关于冷却壁面的实验结果一致。但是壁面局部冷却和全局冷却对不稳定模态的影响不同,根据Sidorenko等[56]的实验和计算发现,局部冷却时,Mack第二模态被抑制,边界层转捩延迟;局部加热时结果相反,转捩位置向上游移动。Polivanov等[57]采用线性稳定性分析及数值模拟方法分别研究了不同的冷却/加热单元对高超声速边界层稳定性的影响。他们发现冷却可以延迟转捩,但是冷却源的位置很重要,不能太靠后 (边界层太厚则冷却源位置上方的扰动放大很明显,导致提前转捩)。Soudakov等[58]发现高超声速飞行器表面热防护层间的温度跳跃将会影响边界层的感受性过程。综上可知,壁面温度对感受性的影响并没有统一的规律,需要考虑模型几何形状的不同、Mack第一模态与Mack第二模态谁是主导等问题。
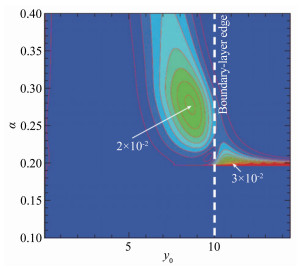
3.3.2 温斑感受性Fedorov等[18, 39, 59-60]详细研究了壁源扰动的感受性问题,包括振动、吹吸、粗糙元以及温斑扰动等。关于壁源温斑扰动的感受性[39, 59],其研究结果显示存在2个快模态对温斑高度敏感的区域,如图 10所示。
第1个区域位于边界层上沿 (见图 3(a)中的区域2),即涡扰动和熵扰动高度集中的区域。在静风洞或者自由飞行中,由于自由声场的忽略不计,涡波、熵波的感受性将在其中起主导作用。第2个区域是在α=0.28, y0≈8.5附近。这个位置和初始温度扰动在边界层内的情况对应,在由激光束[62]或者辉光放电[31, 63]产生扰动的情况中常见。进一步地,他们发现温斑要么可能在区域2产生快模态,进而通过模态转化机制激发Mack第二模态,要么与弓形激波相互作用产生声场进入边界层从而激发Mack第二模态。
之后,Fedorov[64]又发现在Mack第二模态波主导的时候用加热的方法控制层流时,加热源的位置 (离前缘距离及离壁面距离) 不同将产生不同的效果,这和Polivanov等[57]计算结果相吻合。若其在中性点上游且靠近边界层外缘时具有稳定效应;若其在中性点下游且在边界层内部,则稳定效益变弱。在临界层和中性点附近存在最大稳定效应加热点。
3.4 粗糙元感受性实际飞行环境中,为了实现转捩控制或者热防护要求,高超声速飞行器往往有特殊的壁面条件,它们大多可以看成粗糙元。关于低速边界层对粗糙元的感受性研究较多,包括局部粗糙元、分布式粗糙元等[17, 65]。在高超声速边界层方向,粗糙元对转捩的影响是一个热点,但其影响机制仍未清晰[66-73]。高超声速边界层对粗糙元的感受性比低速边界层要复杂得多,其包含了粗糙元和来流声波、涡波的相互作用,涉及横流转捩、尾迹和瞬态增长等过程。Egorov等[74]采用线性稳定性理论 (LST) 和直接数值模拟 (DNS) 方法研究了声场在壁面有多孔敷层 (Porous coating) 的高超声速边界层中的感受性问题,其指出在快声波以0°迎角进入平板时,该敷层能够大幅降低快模态和慢模态的幅值;而慢声波以0°迎角进入平板时,只有慢模态被激发,而且在其初始阶段 (Mack第一模态阶段),多孔敷层对慢模态有轻微的失稳效应,但对Mack第二模态则有稳定作用。当快声波从上表面以45°迎角入射时,由于没有与声场同步,边界层模态未被激发。所有情况均表明多孔敷层对声场仅有微弱影响,也并未因超反射而产生负面效应。Duan等[75]计算高超声速平板边界层在有无表面粗糙元时的感受性,发现扰动幅值的放大或抑制和频率有关。Fong等[76]计算圆锥上粗糙元对边界层稳定性的影响,发现将粗糙元适当地放在同步点后面能够抑制Mack第二模态。Balakumar[77]研究尖锥上二维分布式粗糙元对声波的感受性,发现靠近前缘处的分布式粗糙元能够降低慢声波的感受性,且在粗糙元后的边界层比光滑圆锥时更稳定;而将分布式粗糙元置于同步点附近,则能够提高Mack第二模态对涡波的感受性,但是对快慢声波的感受性则没有影响。通过分析可以发现粗糙元距离同步点的位置、其相对边界层厚度的高度比例等是影响感受性过程的重要因素。
3.5 壁面吹吸感受性Fedorov等[18]通过渐近分析及数值模拟,发现在靠近Mack第二模态的下分支中性曲线附近,边界层对壁面振动和吹吸十分敏感,他们同Wang & Zhong的DNS结果[78]均证实,高超声速边界层对壁面吹吸扰动的感受性要大于对壁面振动及温斑扰动的感受性。
3.6 粒子感受性不论在可压缩还是不可压缩边界层中,粒子诱导转捩是一个不可忽略的因素[79-81]。Fedorov在2013年重点考虑了超声速边界层对粒子的感受性[82],并发现微粒能够在激波层中产生声波进而激发以T-S波主导的转捩机制。而粒子密度似乎对感受性影响不大 (至少对于密度ρ≥1g/cm3时),但是粒径在较低浓度时对感受性影响较为明显。
4 结论感受性问题研究对高超声速边界层的转捩预测至关重要。国际上关于高超声速边界层转捩预测的工具有eN法则[17, 83]、NASP的经验公式[84]等。eN转捩预测准则是结合流动稳定性理论和实验的预测方法。该方法简单描述如下:给定频率的小扰动在边界层内传播,可以用线性化的扰动方程描述。其中扰动的增长率用波数的虚部来描述,N就是扰动幅值的放大倍数:
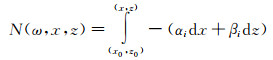 (1)
(1)
式中:(x0, z0) 表示扰动发展的初始位置,αi和βi指流向与展向的增长率,ω表示扰动频率。假定AXN是扰动在不稳定模态下分支中性曲线处 (XN) 的幅值,则下游的扰动幅值可以表示为:
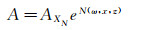 (2)
(2)
在可压缩流实验中,若采用热线测量,由于密度和速度难以解耦,A值需要通过测量边界层内与主流的质量流量脉动M′ b和M′ ∞获得,即A=M′ b/M′ ∞。一般认为当A达到1%~2%时发生转捩,此时A=At, 对应的N记为Nt。工程上一般将Nt取8~11,具体的Nt依赖于AXN的取值。AXN的确定涉及感受性问题,一般由静风洞实验或飞行试验得到。感受性研究最重要的是确定感受性系数。基于来流扰动幅值很小的假设,可以视前缘对外界扰动的感受性过程是线性的,从而定义边界层对扰动的感受性系数[31]如下:
 (3)
(3)
式中:AX0对应前缘扰动幅值。将 (3) 代入 (2) 可以得到:
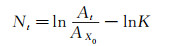 (4)
(4)
从 (4) 中可以看出感受性系数提高10倍,则相同初始扰动幅值下的N-factor减小2.3,可见感受性对eN判据的重要性。因此通过研究感受性问题,获得飞行器在不同的壁面特征 (粗糙元、温度等) 及不同的扰动形式和扰动频率下扰动增长的初始幅值,能更好地预测高超声速飞行器的边界层转捩位置,为飞行器气动设计、热防护等工程应用提供指导。
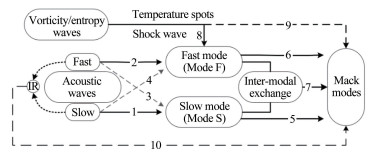
最后,为了更好地理解高超声速边界层感受性问题,总结边界层不稳定波激发的不同路径,如图 11所示。路径1、2、3和4是前缘对声波的感受性,一般1、2路径比3、4路径要强。慢模态向下游发展可能激发Mack不稳定模态,即路径5,但在某些情况如特定频率扰动下对壁面进行冷却时慢模态也可能逐渐衰减。快模态一般会衰减为稳定模态,但有时它也可能发展为Mack不稳定模态,即路径6;快模态还可以通过模态转化机制在同步点附近激发慢模态进而发展成Mack第二模态波即路径7。熵波、涡波可以激发快模态也可以和激波相互作用产生快声波进而激发快模态,即路径8,温斑的感受性过程主要也符合该路径。涡波、熵波进入边界层内,在Mack第二模态下分支中性曲线附近可激发Mack第二模态波 (路径9)。路径10即上文提到的快慢声波非线性相互作用而发展为Mack不稳定模态的情况。上述感受性发展路径可能同时存在并共同导致了边界层内不稳定波的产生,也可能由某一路径主导,需要根据具体的情况而定。当然,由于高超声速边界层感受性过程尚未被充分了解,并不排除存在更本质的机制使得上述某些路径得以统一。最后针对图 11需要指出2点:其一,图中大多数路径依然有待理论的进一步论证,特别是区域2和3的“同步”问题[41],此时快慢模态在上、下游尽管有相同的相速度,但是增长率和特征函数并不相同,需要深入研究其定量关系。其二,图中大多数路径仍待实验的验证。高超声速边界层感受性实验,需要充分考虑模型几何尺寸、噪声水平、扰动频率、扰动位置 (离同步点相对位置)、壁面温度等影响。同时,发展适用于高超声速流动“四高”特点的测量技术,对我国高超声速边界层转捩认识与工程应用将大有裨益。
|
| 图 11 高超声速边界层不稳定波激发的路径 Fig.11 Possible roadmap to unstable mode in hypersonic boundary layer (IR-ineraction) |
| [1] | Schmid P J, Henningson D S. Stability and transition in shear flows[M]. New York: Springer-Verlag, 2001. |
| [2] | Morkovin M V. Bypass transition to turbulence and research desiderata[R]. NASA Lewis Research Center Transition in Turbines, 1985. |
| [3] | Durbin P, Wu X. Transition beneath vortical disturbances[J]. Annual Review of Fluid Mechanics, 2007, 39(1): 107–128. DOI:10.1146/annurev.fluid.39.050905.110135 |
| [4] | Kachanov Y S. Physical mechanisms of laminar-boundary-layer transition[J]. Annual Review of Fluid Mechanics, 1994, 26(1): 411–482. DOI:10.1146/annurev.fl.26.010194.002211 |
| [5] | Lee C B, Wu J Z. Transition in wall-bounded flows[J]. Applied Mechanics Reviews, 2008, 61(3): 030802. DOI:10.1115/1.2909605 |
| [6] | Mack L M. Boundary-layer stability theory[R]. AGRAD-R-709, 1984. |
| [7] | Stetson K, Thompson E, Donaldson J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. Ⅴ-tests with a cooled model[R]. AIAA-89-1895, 1989. |
| [8] | Stetson K, Thompson E, Donaldson J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. Ⅰ-Sharp cone[C]. 16th Fluid and Plasmadynamics Conference, Massachusetts, 1983. |
| [9] | Stetson K, Thompson E, Donaldson J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. Ⅱ-Blunt cone[C]. 22nd Aerospace Sciences Meeting, 1984. |
| [10] | Stetson K, Thompson E, Donaldson J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. Ⅲ-Sharp cone at angle of attack[C]. 23rd Aerospace Sciences Meeting, 1985. |
| [11] | Stetson K, Thompson E, Donaldson J, et al. Laminar boundary layer stability experiments on a cone at Mach 8. Ⅳ-On unit Reynolds number and environmental effects[C]. 4th Joint Fluid Mechanics, Plasma Dynamics and Lasers Conference, 1986. |
| [12] | Bountin D, Sidorenko A, Shiplyuk A. Development of natural disturbances in a hypersonic boundary layer on a sharp cone[J]. Journal of Applied Mechanics and Technical Physics, 2001, 42(1): 57–62. DOI:10.1023/A:1018852410488 |
| [13] | Dong M, Luo J S. Mechanism of transition in a hypersonic sharp cone boundary layer with zero angle of attack[J]. Applied Mathematics and Mechanics, 2007, 28(8): 1019–1028. DOI:10.1007/s10483-007-0804-2 |
| [14] | Pruett C D, Chang C L. Direct numerical simulation of hypersonic boundary-layer flow on a flared cone[J]. Theoretical and Computational Fluid Dynamics, 1998, 11(1): 49–67. DOI:10.1007/s001620050080 |
| [15] | Fezer A, Kloker M. Spatial direct numerical simulation of transition phenomena in supersonic flat-plate boundary layers[M]. Springer Berlin Heidelberg, 2000. |
| [16] | Reshotko E. Boundary-layer stability and transition[J]. Annual Review of Fluid Mechanics, 1976, 8(1): 311–349. |
| [17] | 罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357–372. Luo J S. Transition and prediction for hypersonic boundary layers[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357–372. |
| [18] | Fedorov A V, Khokhlov A P. Receptivity of hypersonic boundary layer to wall disturbances[J]. Theoretical and Computational Fluid Dynamics, 2002, 15(4): 231–254. DOI:10.1007/s001620100052 |
| [19] | Westin K J A, Bakchinov A A, Kozlov V V, et al. Experiments on localized disturbances in a flat plate boundary layer. Part 1. The receptivity and evolution of a localized free stream disturbance[J]. European Journal of Mechanics B-Fluids, 1998, 17(6): 823–846. DOI:10.1016/S0997-7546(99)80016-8 |
| [20] | Borodulin V I, Ivanov A V, Kachanov Y S, et al. Receptivity coefficients at excitation of cross-flow waves by free-stream vortices in the presence of surface roughness[J]. Journal of Fluid Mechanics, 2013, 716: 487–527. DOI:10.1017/jfm.2012.555 |
| [21] | Saric W S, Reed H L, Kerschen E J. Boundary-layer receptivity to freestream disturbances[J]. Annual Review of Fluid Mechanics, 2002, 34: 291–319. |
| [22] | Zhong X L, Wang X W. Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers[J]. Annual Review of Fluid Mechanics, 2012, 44: 527–561. DOI:10.1146/annurev-fluid-120710-101208 |
| [23] | Fedorov A V. Transition and stability of high-speed boundary layers[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 79–95. DOI:10.1146/annurev-fluid-122109-160750 |
| [24] | Balakumar P. Receptivity of hypersonic boundary layers to acoustic and vortical disturbances (invited)[C]. 45th AIAA Fluid Dynamics Conference, 2015. |
| [25] | McKenzie J F, Westphal K O. Interaction of linear waves with oblique shock waves[J]. Physics of Fluids, 1968, 11(11): 2350–2362. DOI:10.1063/1.1691825 |
| [26] | Ma Y B, Zhong X L. Receptivity of a supersonic boundary layer over a flat plate. Part 2. Receptivity to free-stream sound[J]. Journal of Fluid Mechanics, 2003, 488: 79–121. DOI:10.1017/S0022112003004798 |
| [27] | Fedorov A V, Khokhlov A P. Excitation of unstable modes in a supersonic boundary layer by acoustic waves[J]. Fluid Dyna-mics, 1991, 26(4): 531–537. |
| [28] | Fedorov A V, Khokhlov A P. Excitation and evolution of unstable disturbances in supersonic boundary layer[C]. Proceedings of ASME Fluid Engineering Conference, 1993, 151:1-13. |
| [29] | Fedorov A V, Tumin A. Initial value problem for hypersonic boundary layer flows[C]. 15th AIAA Computational Fluid Dynamics Conference, 2001. |
| [30] | Herbert T, Lin N A Y. Studies of boundary-layer receptivity with parabolized stability equations[C]. 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, 1993. |
| [31] | Maslov A A, Shiplyuk A N, Sidorenko A A, et al. Leading-edge receptivity of a hypersonic boundary layer on a flat plate[J]. Journal of Fluid Mechanics, 2001, 426: 73–94. DOI:10.1017/S0022112000002147 |
| [32] | Schneider S P. Development of hypersonic quiet tunnels[J]. Journal of Spacecraft & Rockets, 2008, 45(45): 641–664. |
| [33] | 张传鸿. 高超声速静风洞的调试及圆锥边界层转捩的实验研究[D]. 北京: 北京大学, 2014. Zhang C H. The development of hypersonic quiet wind tunnel and experimental investigation of hypersonic boundary-layer transition on a flared cone[D]. Beijing:Peking University, 2014. |
| [34] | Zhang C, Lee C. Rayleigh-scattering visualization of the deve-lopment of second-mode waves[J]. Journal of Visualization, 2016: 1–6. |
| [35] | Fedorov A V, Khokhlov A P. Sensitivity of a supersonic boundary layer to acoustic disturbances[J]. Fluid Dynamics, 1992, 27(1): 29–34. DOI:10.1007/BF01054169 |
| [36] | Fedorov A V, Khokhlov A P, Khokhlov P. Prehistory of instability in a hypersonic boundary layer[J]. Theoretical and Computational Fluid Dynamics, 2001, 14(6): 359–375. DOI:10.1007/s001620100038 |
| [37] | Ma Y B, Zhong X L. Numerical simulation of receptivity and stability of nonequilibrium reacting hypersonic boundary layers[C]. 39th Aerospace Sciences Meeting and Exhibit, 2001. |
| [38] | Fedorov A V. Receptivity of a high-speed boundary layer to acoustic disturbances[J]. Journal of Fluid Mechanics, 2003, 491: 101–129. DOI:10.1017/S0022112003005263 |
| [39] | Fedorov A V, Tumin A. Initial-value problem for hypersonic boundary-layer flows[J]. AIAA Journal, 2003, 41(3): 379–389. DOI:10.2514/2.1988 |
| [40] | Ma Y B, Zhong X L. Receptivity of a supersonic boundary layer over a flat plate. Part 1:Wave structures and interactions[J]. Journal of Fluid Mechanics, 2003, 488: 31–78. DOI:10.1017/S0022112003004786 |
| [41] | 周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M]. 北京: 科学出版社, 2015. Zhou H, Su C H, Zhang Y M. Transition mechanism and prediction of supersonic/hypersonic boundary layers[M]. Beijing: Science Press, 2015. |
| [42] | Ma Y B, Zhong X L. Receptivity of a supersonic boundary layer over a flat plate. Part 3. Effects of different types of free-stream disturbances[J]. Journal of Fluid Mechanics, 2005, 532: 63–109. DOI:10.1017/S0022112005003836 |
| [43] | Gao J, Luo J S, Wu X S. Receptivity of hypersonic boundary layer due to fast-slow acoustics interaction[J]. Acta Mechanica Sinica, 2015, 31(6): 899–909. DOI:10.1007/s10409-015-0504-8 |
| [44] | 张玉东, 傅德薰, 马延文, 等. 钝锥高超声速边界层来流感受性数值研究[J]. 中国科学, 2008, 38(9): 1246–1254. Zhang Y D, Fu D X, Ma Y W, et al. Receptivity to free-stream disturbance waves for hypersonic flow over a blunt cone[J]. Science in China, Series G:Physics, Mechanics and Astronomy, 2008, 38(9): 1246–1254. |
| [45] | Shi J, Tang X, Wang Z, et al. Receptivity of boundary layer over a blunt wedge due to freestream pulse disturbances at Mach 6[J]. International Journal of Aerospace Engineering, 2016(1): 1–14. |
| [46] | Kara K, Balakumar P, Kandil O. Receptivity of hypersonic boundary layers due to acoustic disturbances over blunt cone[C]. AIAA Aerospace Sciences Meeting and Exhibit, 2007. |
| [47] | Balakumar P, Kegerise M A. Receptivity of hypersonic boundary layers over straight and flared cones[J]. AIAA Journal, 2015, 53(8): 2097–2109. DOI:10.2514/1.J053432 |
| [48] | Zhong X L, Lei J. Numerical simulation of nose bluntness effects on hypersonic boundary layer receptivity to freestream disturbances[R]. AIAA-2011-30379. |
| [49] | Potter J L. Review of the influence of cooled walls on boundary-layer transition[J]. AIAA Journal, 1980, 18(8): 1010–1012. DOI:10.2514/3.7703 |
| [50] | Stetson K F, Kimmel R L. Surface temperature effects on boundary-layer transition[J]. AIAA Journal, 1992, 30(11): 2782–2783. DOI:10.2514/3.11300 |
| [51] | Kara K, Balakumar P, Kandil O. Effects of wall cooling on hypersonic boundary layer receptivity over a cone[C]. 38th Fluid Dynamics Conference and Exhibit, 2008. |
| [52] | Blanchard A E. Investigation of wall-cooling effects on hypersonic boundary-layer stability in a quiet wind tunnel[D]. Norfolk, VA:Old Dominion University, 1995. |
| [53] | Demetriades A. New experiments on hypersonic boundary layer stability including wall temperature effects[C]//Proceedings of the 1978 Heat Transfer and Fluid Mechanics Institute, 1978:39-54. |
| [54] | Decarlo J P, Sanator R J, Torrillo D T. Hypersonic boundary-layer transition data for a cold-wall slender cone[J]. AIAA Journal, 1965, 3(4): 758–760. DOI:10.2514/3.2969 |
| [55] | Lysenko V I, Maslov A A. The effect of cooling on supersonic boundary-layer stability[J]. Journal of Fluid Mechanics, 1984, 147: 39–52. DOI:10.1017/S002211208400197X |
| [56] | Sidorenko A, Gromyko Y, Bountin D, et al. Effect of the local wall cooling/heating on the hypersonic boundary layer stability and transition[J]. EUCASS Proceedings Series-Advances in AeroSpace Sciences, 2015, 7: 549–568. |
| [57] | Polivanov B P, Gromyko Y, Sidorenko A, et al. Effects of local wall heating and cooling on hypersonic boundary-layer stability[C]. Proceedings of the Summer Program 2011, 2011. |
| [58] | Soudakov V, Egorov I, Fedorov A. Numerical simulation of receptivity of a hypersonic boundary layer over a surface with temperature jump[C]. ESA Special Publication, 2009, 659. |
| [59] | Fedorov A V, Ryzhov A A, Soudakov V G, et al. Receptivity of a high-speed boundary layer to temperature spottiness[J]. Journal of Fluid Mechanics, 2013, 722: 533–553. DOI:10.1017/jfm.2013.111 |
| [60] | Egorov I V, Sudakov V G, Fedorov A V. Numerical modeling of the stabilization of a supersonic flat-plate boundary layer by a porous coating[J]. Fluid Dynamics, 2006, 41(3): 356–365. DOI:10.1007/s10697-006-0051-x |
| [61] | Fedorov A. Transition and stability of high-speed boundary layers[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 79–95. DOI:10.1146/annurev-fluid-122109-160750 |
| [62] | Schmisseur J D, Schneider S P, Collicott S H. Supersonic boundary-layer response to optically generated freestream disturbances[J]. Experiments in Fluids, 2002, 33(2): 225–232. DOI:10.1007/s00348-001-0392-5 |
| [63] | Kosinov A D, Maslov A A, Shevelkov S G. Experiments on the stability of supersonic laminar boundary-layers[J]. Journal of Fluid Mechanics, 1990, 219: 621–633. DOI:10.1017/S0022112090003111 |
| [64] | Fedorov A V, Ryzhov A A, Soudakov V G, et al. Numerical simulation of the effect of local volume energy supply on high-speed boundary layer stability[J]. Computers & Fluids, 2014, 100: 130–137. |
| [65] | Kuester M S, White E B. Roughness receptivity and shielding in a flat plate boundary layer[J]. Journal of Fluid Mechanics, 2015, 777: 430–460. DOI:10.1017/jfm.2015.267 |
| [66] | Balakumar P. Boundary layer receptivity due to roughness and freestream sound for supersonic flows over axisymmetric cones[C]. 38th Fluid Dynamics Conference and Exhibit, Seattle, Washington, 2008. |
| [67] | Iyer P S, Muppidi S, Mahesh K. Roughness-induced transition in high speed flows[C]. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, 2011. |
| [68] | Reda D C. Review and synthesis of roughness-dominated transition correlations for reentry applications[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 161–167. DOI:10.2514/2.3803 |
| [69] | Schneider S P. Effects of roughness on hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 193–209. DOI:10.2514/1.29713 |
| [70] | Schneider S P. Summary of hypersonic boundary-layer transition experiments on blunt bodies with roughness[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1090–1105. DOI:10.2514/1.37431 |
| [71] | Wang X, Zhong X. Receptivity of a hypersonic flat-plate boundary layer to three-dimensional surface roughness[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1165–1175. DOI:10.2514/1.37766 |
| [72] | Mistry V I, Page G J, McGuirk J J. Simulation of receptivity and induced transition from discrete roughness elements[J]. Flow, Turbulence and Combustion, 2015, 95(2): 301–334. |
| [73] | Tang Q, Zhu Y D, Chen X, et al. Development of second-mode instability in a Mach 6 flat plate boundary layer with two-dimensional roughness[J]. Physics of Fluids, 2015, 27(6): 064105. DOI:10.1063/1.4922389 |
| [74] | Egorov I V, Fedorov A V, Soudakov V G. Receptivity of a hypersonic boundary layer over a flat plate with a porous coating[J]. Journal of Fluid Mechanics, 2008, 601: 165–187. |
| [75] | Duan L, Wang X W, Zhong X L. A high-order cut-cell method for numerical simulation of hypersonic boundary-layer instability with surface roughness[J]. Journal of Computational Phy-sics, 2010, 229(19): 7207–7237. DOI:10.1016/j.jcp.2010.06.008 |
| [76] | Fong K D, Wang X W, Huang Y T, et al. Second mode suppression in hypersonic boundary layer by roughness:design and experiments[J]. AIAA Journal, 2015, 53(10): 3138–3143. DOI:10.2514/1.J054100 |
| [77] | Balakumar P. Receptivity of hypersonic boundary layers to distributed roughness and acoustic disturbances[C]. 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2013. |
| [78] | Wang X W, Zhong X L. Effect of wall perturbations on the receptivity of a hypersonic boundary layer[J]. Physics of Fluids, 2009, 21(4): 044101. DOI:10.1063/1.3103880 |
| [79] | Ladd D M, Hendricks E W. The effect of background particulates on the delayed transition of a heated 9-1 ellipsoid[J]. Experiments in Fluids, 1985, 3(2): 113–119. |
| [80] | Lauchle G C, Petrie H L, Stinebring D R. Laminar-flow performance of a heated body in particle-laden water[J]. Experiments in Fluids, 1995, 19(5): 305–312. |
| [81] | Holden M S. Studies of transitional flow, unsteady separation phenomena and particle induced augmentation heating on ablated nose tips[R]. AFOSR-TR-76-1066, 1975. |
| [82] | Fedorov A V, Tumin A. High-speed boundary-layer instability:old terminology and a new framework[J]. AIAA Journal, 2011, 49(8): 1647–1657. DOI:10.2514/1.J050835 |
| [83] | Van Ingen J L. The eN method for transition prediction:historical review of work at TU delft[C]. 38th Fluid Dynamics Conference and Exhibit, 2008. |
| [84] | Lau K Y. Hypersonic boundary-layer transition:application to high-speed vehicle design[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 176–183. DOI:10.2514/1.31134 |