2. 北京交通大学 土木建筑工程学院, 北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
近30年来,应用图像处理技术观测推移质运动取得了丰富的成果,有力推动了河流动力学研究的进展。目前,基于高频摄像机的图像测量系统已经在明渠水槽试验测量中得到成功应用。在室内水槽试验中,常常采取侧面拍摄[1-2]和俯视拍摄[2-3]2种方式来记录推移质颗粒的运动图像。俯视拍摄能够获得群体颗粒在床面附近的运动特征,观测效率大大提高,但由于背景复杂,图像处理难度也增大。不论采取侧面拍摄还是俯视拍摄,由于推移质在时空尺度上的间歇性与随机性,使得图像测量参数的选取对推移质运动结果产生不可忽略的影响。
由于推移质运动具有非连续的特点,若使用不同的采样间隔(Δt),测得的运动参数并不一致。在理论上,提高时间分辨率,采用较小的Δt进行测量,可以获取更精细的推移质运动信息;但在实际试验中,若采用很小Δt,颗粒在2帧之间的位移可能太小以至于无法有效识别。Radice等[5]指出,Δt的合理值应该对应于Nikora等[6]提出的推移质运动的中间尺度,但未对中间尺度内的Δt对推移质输沙结果的影响进行定量研究。
床面推移质运动在空间上也呈现出显著的非均匀性。文献[3-7]发现,运动颗粒的位置在空间上的分布存在各项异性。这种不均匀的空间分布被认为可能与水流相干结构有关[8-9]。因此若对推移质运动结果进行空间平均,需要考虑运动颗粒分布的空间特性,选择合理的采样面积。同时,由于推移质运动在时间尺度上具有随机性,根据统计理论可知,若采用时间平均的方法获取推移质运动结果,则结果能否收敛取决于相互独立的样本数量或者连续采样的样本时长。文献[3]研究发现随着采样面积的增大,运动颗粒数量的变异系数越低,即波动性越弱,但未分析合理的采样面积值。
在俯视拍摄方法的研究中,研究者[3-5, 10-13]采用不同的采样间隔Δt、采样床面范围A、采样时长Rt和颗粒直径D等。在上述文献中,采样间隔的范围为1/25~1/250s,采样面积范围为0.015~0.46m2,采样时长的范围0.5~1800s,颗粒直径从0.5mm到8mm不等。不同研究者使用的参数有很大差别,但对试验参数如何影响推移质测量结果尚缺乏定量研究,对如何选取合适的参数远未达成共识。
本文利用高速摄像机俯视拍摄封闭槽道中推移质的运动图像,采用图像处理的方法获取颗粒的运动比例和运动速度,定量分析不同参数(样本数量、采样时长、采样间隔、采样面积)对测量结果(运动比例、运动速度及输沙率)的影响,对试验参数选取提出初步建议并对本文的试验方法进行讨论。
1 研究方法本文试验选择在有压槽道中进行,文献研究[14]发现在弗汝德数小于0.5的封闭槽道中推移质起动与输移规律与明渠中是基本一致的,因此本文的结果对明渠输沙研究也有参考价值。
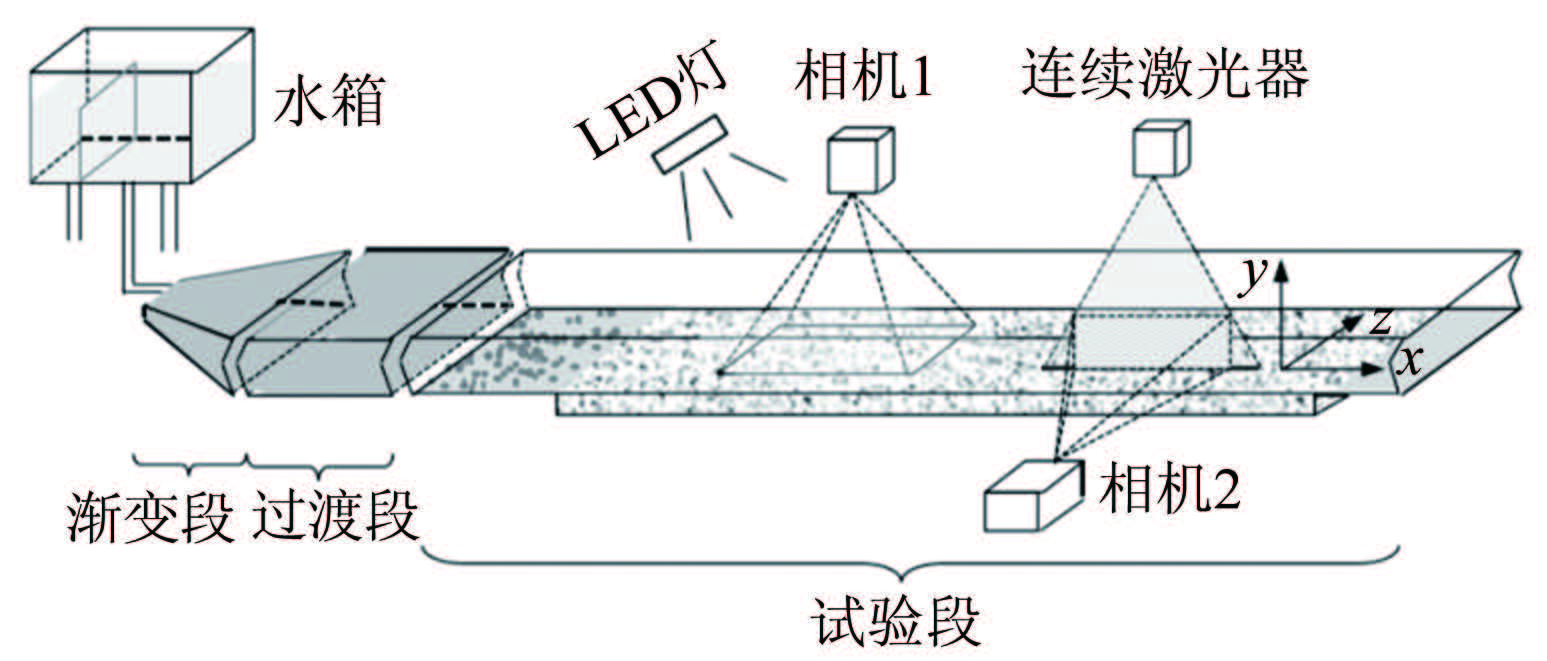
1.1 槽道系统有压槽道长、宽、高分别为6.4、0.25和0.2m,见图 1。槽道由可升降水箱(最大提升高度为8m)提供压力水头(水箱内放置薄壁堰以保证压力水头稳定),槽道入口与水箱通过软管和渐变段连接,槽道出口同样连接渐变段和排水软管,保证水流平稳。流量测量和控制通过安装在出口排水软管上的电磁流量计(0~90m3/h)和蝶形电动阀门(0~0.3MPa)实现。槽道可分为上、下游过渡段和中部试验段,长度分别为2.2、2.2和2m。过渡段材料为不锈钢,而试验段则由钢化玻璃制成,可从各个侧面进行观测。观测段的底板比上下游过渡段底板低5cm。试验时观测段平整铺满推移质天然沙(5cm厚),在进口段粘一层同样粒径的沙粒,保持整个槽道底板平齐及糙率一致。
|
| 图 1 试验布置示意图 Fig.1 Sketch of experimental setup |
试验开始时,为避免扰动试验段床面的平整铺沙,先将槽道进出口的阀门关闭,从进水软管缓慢地注水至灌满槽道,然后开启阀门,由水箱提供压力驱动,调节水流至试验设计条件。本文仅研究低强度输沙,在槽道进口不提供泥沙补给,试验观测需要在床面出现明显的形态变化之前结束。
定义沿水流方向为x轴,沿水深竖直向上为y轴,沿展向为z轴,坐标原点位于床面中心线。试验使用的推移质泥沙为均匀粒径天然砂,粒径D为1mm,密度ρs为2650kg/m3,对应的临界起动Shields数Θc=0.036[15]。试验中压力水头保持5.4m不变,通过改变阀门开度控制流量,研究了3种流量情况,分别为:67.8、71.6和75m3/h。
1.2 流速测量采用时序粒子图像测速系统(TR-PIV)测量观测段槽道中心线的流场分布(见图 1)。连续激光器(8W)置于槽道正上方,激光片光源垂直向下照亮槽道中心线上的xy平面,水流示踪粒子(直径为10μm的空心玻璃珠)的运动图像由置于侧面的高频相机(相机2)拍摄,满帧画幅为2336pixel×1728pixel,PIV采样频率设定为符合四分之一法则的要求。为降低粒子拖尾的影响,所有试验组次的曝光频率均采用250μs。关于图像测速(TR-PIV)系统测量的详细参数可以参考文献[16]。
对于每一试验组次,拍摄4000帧图片,通过图像分析处理,获得2000个瞬时速度流场样本,对瞬时流场进行统计可以得到时均流场和雷诺应力分布。
关于摩阻流速u*的获取,选取适应于有压粗糙床面槽道流的雷诺应力外延法获取。在0.2<y/h<0.8的区间(y为距理论床面的高度,h为槽道半高),水流切应力中的粘性应力部分可以忽略不计,切应力沿水深线性变化,因此将此区间的雷诺应力延长至y/h=0处,则可以得床面切应力τ,从而可计算出u*。
对于动床试验,对于理论床面(y=0)的选取尚有争议。本文的简化做法是:选取床面颗粒最高点以下0.2D的位置作为理论零点[17]。
1.3 推移质运动测量推移质运动图像的获取采用俯视拍摄法,CCD相机拍摄最大画幅为640pixel×l480pixel(相机1),相应的采样频率为245帧/s。可以通过减小画幅来提高采样频率,本试验采用最大拍摄频率Fmax为315帧/s,即最小采样间隔Δt约为0.003s,相应的拍摄画幅为640pixel×300pixel,图像分辨率R=7.7pixel/mm。 采用立体均匀的打光方式为床沙补光(见图 1),以增加图像亮度,相机曝光时间控制在100μs以内以避免粒子拖尾造成误差。
对图像首先采取顶帽变换、均衡化及高斯滤波进行预处理,消除不均匀的背景、较大的气泡和杂质,并整体提高图片亮度。其后,采用图像相减法获取推移质运动颗粒的位置,该方法基于泥沙运动导致的2帧图像中相应位置的灰度值发生变化的原理,通过统计图像相减后为负值或正值的区域个数,标记出运动颗粒的中心点位置,该方法详细介绍参见文献[18]。最后,采用PIV算法方法计算运动颗粒的位移。选取以单颗粒椭圆长轴为边长的正方形作为计算窗口,进行连续2帧图像一定范围内的互相关计算,将互相关系数峰值点与颗粒原点的距离做为运动颗粒的位移。
获取运动颗粒数目及颗粒运动速度的具体操作步骤如下:
(1) 用g1(i,j)和g2(i,j)标记2帧图片的灰度值矩阵,通过图像相减得到灰度值发生变化区域的初始位置(I,J);
(2) 通过统计图像相减后为正值(或负值)的区域个数,得到运动颗粒数目的估计值N1;
(3) 设定(ΔI,ΔJ)为颗粒运动位移的可变参数,应用式(1)计算互相关系数:
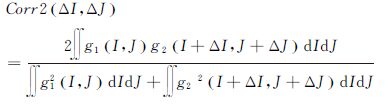 (1)
(1)
(4) 采用亚像素精度拟合寻找互相关系数峰值点,峰值点对应的(ΔIp,ΔJp)即为颗粒位移。若位移峰值大于给定的阈值,则可计算颗粒运动速度Ub;若实际峰值小于阈值,则认为该峰值位移可能是由某种扰动引起,并不代表实际颗粒运动,进而得到运动颗粒数目的实际值N。
峰值点位移的阈值选择对结果有重要影响,阈值过低会导致颗粒的错误匹配,过高则会使较暗的运动颗粒匹配失败。在本试验的图像质量下,经反复检验,位移阈值取0.4~0.6pixel之间时匹配的正确率最高,最终选取位移阈值为0.5pixel。这相当于定义位移大于0.5pixel的颗粒为有效运动颗粒。上述方法在处理标准颗粒位移图片时其正确率为100%(标准图片的生成方法见文献[19])。
获得整个床面拍摄范围(面积记为A)内推移质运动的个数N之后,可以计算床面推移质运动的比例:
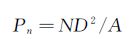 (2)
(2)
显然式(2)仅适用于床沙无间隙排列的情况,本试验条件与此相近。
在低强度输沙(表层输移)条件下,无量纲推移质单宽输沙率(推移质运动强度)可直接计算得出:
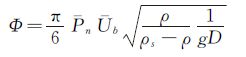 (3)
(3)
其中Ub和Pn为得到的推移质运动流向速度平均值和运动比例的平均值,ρ=1000kg/m3表示水密度,g=9.81m/s2为重力加速度。
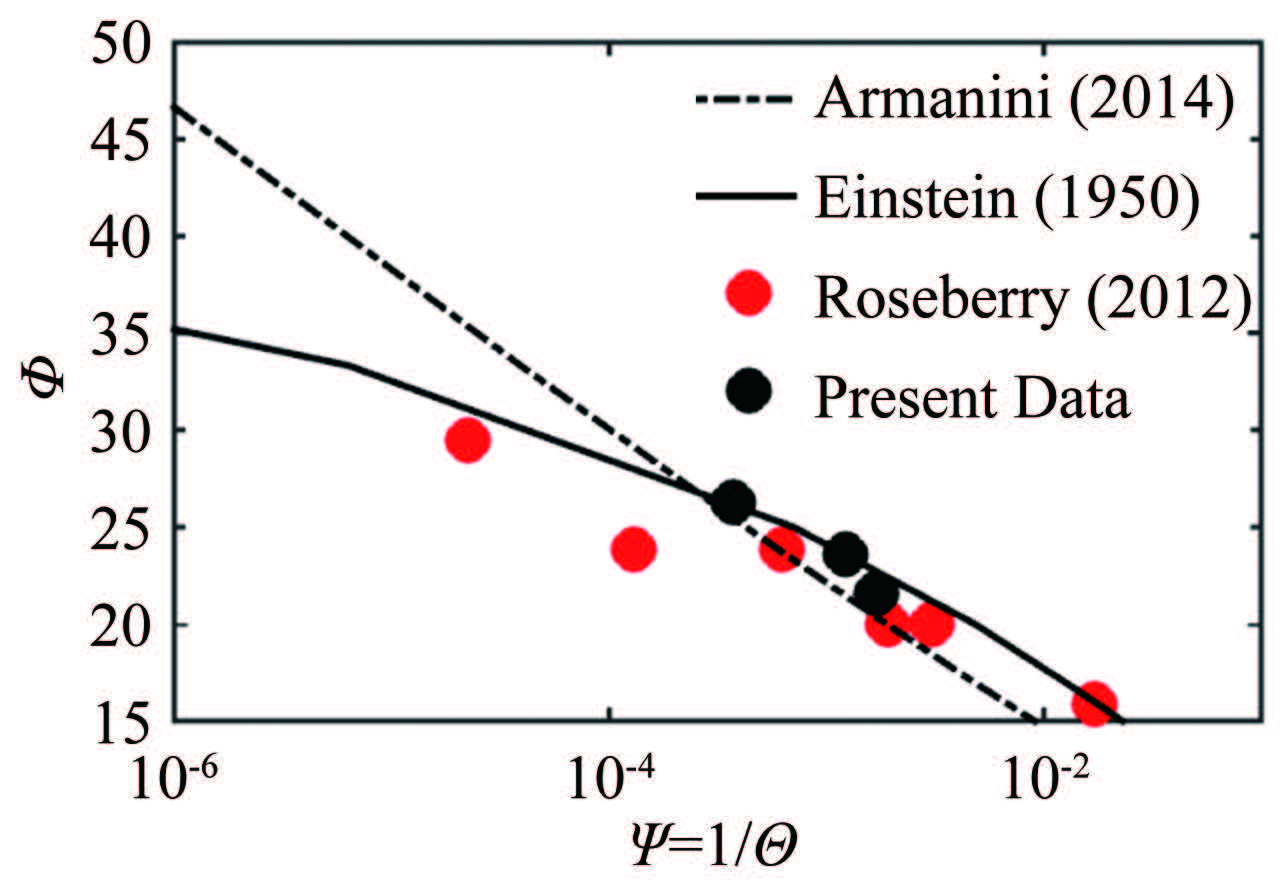
1.4 试验组次共进行了3组试验,试验条件在表 1中列出。各组试验的压力水头均为5.4m。对于每一组次的试验,将改变样本容量、采样时长、采样间隔和采样区域,观察这些参数对测量结果的影响。表 1中出的Ub、Pn和Φ值,对应的是本试验采用的最高频最大画幅及最长时间序列下进行时空平均的结果。将此结果绘制在图 2中,与Armanini[20]和Einstein[21]的经典公式,以及Roseberry[3]发表的实验数据进行对比,发现本文在高频大画幅及长时间序列下获取的数据与经典公式吻合,这也说明利用本文的实验方法获取推移质输沙的可靠性。
|
组 次 | U /(cm·s-1) | u* /(cm·s-1) | Re* | Θ /10-2 | Pn /% | Ub /(cm·s-1) | Φ /10-2 |
| C1 | 37.67 | 2.48 | 25.83 | 3.80 | 0.097 | 9.26 | 0.037 |
| C2 | 39.78 | 2.62 | 28.58 | 4.24 | 0.320 | 9.34 | 0.123 |
| C3 | 41.67 | 2.74 | 29.89 | 4.64 | 0.440 | 9.39 | 0.170 |
|
| 图 2 推移质输沙率随Shields数的变化规律 Fig.2 Variations of Φ with 1/Θ |
其中颗粒雷诺数Re**=u*D/υ,υ为水流运动粘滞系数;Shields数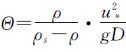
如引言中所述,本试验采取时空双平均的方法获取推移质运动的统计结果,因此需获取使结果收敛的独立样本容量Sz及采样历时Rt。
试验中选择在最小间隔(1/315s)下采样,共采集100 000对图片,历时315s。通过分析拍摄的100 000对图片,得到99 999个原始样本数据(瞬时欧拉场)。在实际分析时,首先选定要研究的样本容量,采取从原始流场序列中等距抽取样本的方法。样本容量与采样历时组合的选取方法如表 2所示。以Sz=5000为例,若隔1取1来抽样,对应的采样历时为Rt=5000×2/315≈31.75s;若隔10取1,则对应的采样历时扩大到153.73s,为原始流场采样历时的一半。采样历时反映了样本的相互独立性,一般认为抽样的间隔越大即采样历时越长,样本之间的关联性越弱。
| 序号 | Sz | Rt/s |
| 1 | 100 | 100n/315,n= 2,3,4,…,1000 |
| 2 | 1000 | 1000n/315,n= 2,3,4,…,100 |
| 3 | 5000 | 5000n/315,n= 2,3,4,…,20 |
| 4 | 10 000 | 10 000n/315,n=2,3,4,…,10 |
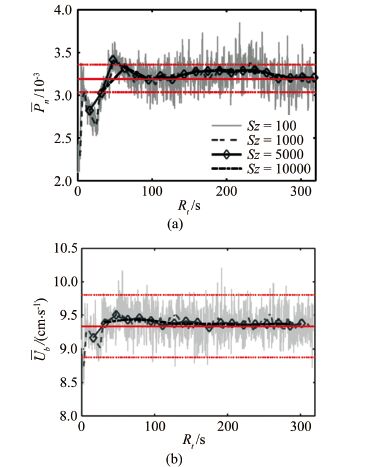
计算不同Sz和Rt组合下推移质运动的Pn和Ub数值,可以定量观察统计参数随样本容量和采样历时的变化特点。图 3给出了C2组次试验的具体结果,其中红色实线和虚线分别代表真实值及95%的置信范围。
|
| 图 3 Pn及Ub随样本容量及采样历时的变化规律 Fig.3 Variations of Pn and Ub with Sz as well as Rt |
从图 3可以看出如下基本特点:
(1) Pn和Ub随采样历时的收敛速度有明显差异。Pn收敛到95%置信水平需要的采样历时约为80s,而Ub在最小采样历时下(12.7s)已经达到该置信水平,这是由于以图片对为样本容量时,每对图片仅有1个Pn值,但存在多个Ub值,因此Ub更易收敛。
(2)从整个趋势上看,随着Sz和Rt的增大,Pn和Ub的离散程度降低。但当样本容量比较小时(以Sz=100为例),即使增大采样历时,计算结果仍呈现出相对较大的离散度;当采样历时比较短时(以Rt<10s为例),即使增大样本容量也并不能有效提高结果的可靠性,即样本之间的关联性较强。
(3)当Sz=1000和Rt=80,即隔25取1时,样本之间独立性较强且结果基本收敛。就本文的试验条件而言,取Sz=5000和Rt=100s的组合,结果可以达到98%~99%的置信水平。
2.2 采样间隔的影响采样间隔会影响推移质运动参数的测量结果,而这种影响与两方面的因素有关。一方面,采样间隔会影响图像处理中位移相关算法和粒子匹配算法;另一方面,推移质运动的间歇性导致在不同的采样间隔下得到的结果有所差异。
为保证位移相关计算的精度要求,推移质颗粒在2帧图片之间的位移应大于1个像素[5],由此可反算出采样间隔的最小值,即:
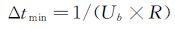 (4)
(4)
按照本文R=7.7pixel/mm及Ub=9.39cm/s(C3组次,见表 1),对应的最小采样间隔约为1/723s。
本试验中分析C2组次在不同采样间隔下测得的推移质运动参数变化情况,采样面积选取最大值。不同采样频率的获取方法为:从原始图片序列中以固定间隔抽取图像得到一系列子图像序列。本文采取的固定间隔图片为0,1,3,5,7,9和15,从而得到采样间隔为1/315,2/315,3/315,5/315,7/315,9/315和15/315s这7种间隔的图像序列,对应的采样时长均为315s,最大样本容量为100 000,最小样本容量约为6666(100 000/15)。按照前述分析,所采用的采样历时和样本容量是合适的。
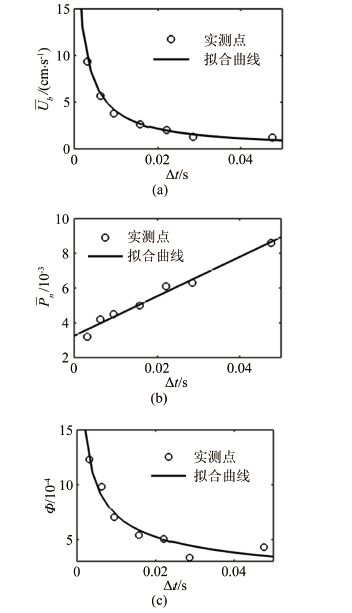
实际结果如图 4所示。由图可见,Ub与Δt大致呈反比关系;Pn随Δt线性增加,二者随Δt变化的趋势与引言中分析一致。需要指出的是,随Δt的增大,对Pn进行拟合的直线斜率减小,这可能是由于大时间间隔下颗粒相互覆盖的情况多有发生,计算分析错误率增加,因此得到的Pn和Ub可信度要低一些。图 4(c)显示的推移质输沙率根据公式3计算得到,随Δt的增加而明显减小。在本文的条件下,输沙率最大值约为最小值的3倍左右。
|
| 图 4 Pn、Ub及Φ随采样间隔的变化规律 Fig.4 Variations of Pn,Ub and Φ with Δt |
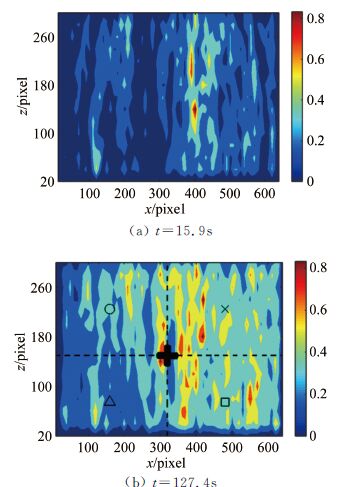
已有研究表明[3, 7],在低强度水流条件下,推移质运动在空间分布不均。在低强度输沙条件下,床面形态变化较小,直接观测床面高程变化存在较大的相对误差。本文采用另外一种简单方法来直观展示推移质运动空间分布特点,该方法将一定时长内床面各局部区域发生运动的推移质颗粒数量进行对比。本文对C2试验组次2个典型时长进行了对比分析,分别为15.9和127.4s(对应的样本容量分别5000和40 000),采样间隔均为1/315s,结果如图 5所示。从图中可以看出,床面局部区域运动颗粒数量较多,相邻部分区域颗粒运动较少,2种类型的区域沿展向(z轴)间隔分布,形成类似条带状的分布特征,且随采样时间的增长,条带位置基本不变。需要指出的是,图中沿展向除条带状分布特征外,还出现中间运动个数多、两侧少的现象,这主要是由边壁效应所致,在已有的试验[7]中同样出现由边壁效应引发的此类现象。
|
| 图 5 运动颗粒在空间上分布 Fig.5 Spatial distribution of moving particles |
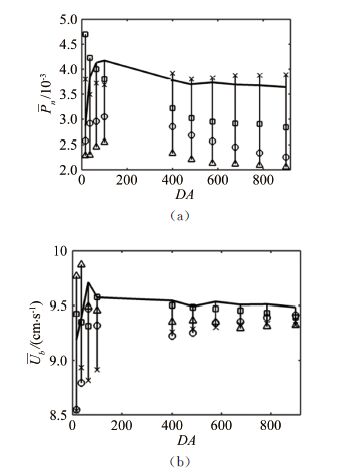
为对采样面积的影响进行定量分析,本试验选取不同采样面积来分析C2组次下推移质运动测量结果,选取的采样间隔为1/315s,在100s采样时间内间隔选取5000个样本进行统计。采用颗粒直径的平方对面积进行无量纲化,即DA=A/D2。首先,以图片中心点为固定中心点(如图 5(b)中心处黑色十字点),按正方形划定采样区间,研究10种尺寸情况,对应的面积为DA=16,36,64,100,400,484,576,676,784和900。在各种采样面积下,统计分析推移质运动比例及速度的均值。如图 6所示,其中黑色实线代表 10种采样空间尺寸下Pn与Ub的值,结果表明,在DA<100时,Ub与Pn随采样面积增大而增大,这是由于基准点恰好选在推移质运动数量少的位置,当扩大采样面积,将最先取到运动数量多的部分,因此呈现一种陡增的趋势;随着采样面积的增大,边壁效应逐渐显现,将导致Pn缓慢地减小。本文以最大面积下的统计值作为统计真实值,认为在不同采样面积下Pn达到统计真实值的90%置信水平时,其结果具有代表性,根据此种判定方法,DA≥400时,结果收敛且能够代表统计真实值。
|
| 图 6 Pn及Ub随无量纲采样区间的变化规律 Fig.6 Variations of Pnand Ubwith dimensionless sampling area |
由于运动颗粒在空间的分布不均,从图 5(b)中可以看出,在相同的采样面积下,若选取的基准点不同,其统计结果也会有所差别。为将此种差别定量化,将最大采样面积均匀地分为4个部分,选取每个部分的中心点作为基准点(如图 5(b)中黑色圆圈、方框、三角及叉点),以此统计不同基准点下正方形采样面积内的Ub与Pn的值(采用与基准点相同的标志展示结果)。由图 6可见,Pn在中心点及右上基准点的取值较大(图 6(a)),在左下方基准点(三角)的值较小,与图 5(b)的分布相符;而Ub的取值随基准点位置变化没有明显的规律(图 6(b)),在DA≥400时,Ub随基准点的位置变化较小,在中心点处的运动速度最大。从运动颗粒在空间的分布可知,Pn受基准点位置的影响较大,为使得结果具有代表性,尽量选择水槽中心的位置为基准点。
3 结论与讨论在有压封闭槽道中采用高频图像测量手段进行了多组试验,研究了试验参数对推移质测量结果的影响。通过具体分析得到以下结论:
(1) 样本容量及采样时长均会影响推移质运动测量结果,在本试验条件下取样本容量5000、采样时长100s的组合,能够满足统计需求。
(2) 采样间隔的极值受图像处理手段的限制,最小采样间隔对应位移大于1个像素,在本文试验条件下对应的采样间隔最小值为1/723s。
(3) 实际测量结果则表明:颗粒平均运动速度与采样间隔成反比,推移质平均运动比例与采样间隔为线性正比关系,而由二者计算得到的推移质输沙率随采样间隔增加而减小。
(4) 运动颗粒在平面上的分布沿展向呈现条带状结构,为保证统计结果具有代表性,要求无量纲的采样面积大于400,且选择水槽中心为图片中心点。
值得指出的是,本文的推移质输沙率是根据颗粒运动比例与速度计算得到,并非直接测量结果。若试验采用水槽尾部称重的方法直接测量推移质平衡输沙率,其结果必不随采样间隔变化。之所以出现本文的结论,可能是由于图像处理方法导致。虽然本文采用的方法通过标准图片进行验证,但仍存在2个重要问题:一是极小间隔的图片对易获取发生晃动而非运动的颗粒,二是处理大间隔下的图片对时,颗粒的运动距离较长容易发生形变及相互覆盖,从而使匹配错误率增加。这2个问题有可能导致小间隔下的颗粒运动个数较实际多,大间隔下的颗粒运动个数较实际少。从这种角度出发,若图像处理方法能够获取单颗粒的运动轨迹,即对运动颗粒进行目标追踪,则有可能减弱上述问题的影响。但是由于已有文献中采取与本文相同的图像处理方法,因此仍将输沙率随采样间隔的变化作为在此种试验方法下的结论。
| [1] | Ancey C, Bigillon F, Frey P, et al. Rolling motion of a bead in a rapid water stream[J]. Physical review E, 2003, 67(1): 011303. DOI:10.1103/PhysRevE.67.011303 |
| [2] | 胡春宏, 惠遇甲. 水流中颗粒跃移参数的试验研究[J]. 水动力学研究与进展, 1991, 6: 71–81. Hu C H, Hui Y J. Experimental study of saltation of solid grains in open channel flow[J]. Journal of Hydrodynamics, 1991, 6: 71–81. |
| [3] | Roseberry J C, Schmeeckle M W, Furbish D J. A probabilistic description of the bed load sediment flux: 2. Particle activity and motions[J]. Journal of Geophysical Research: Earth Surface (2003-2012), 2012, 117(F3). |
| [4] | Lajeunesse E, Malverti L, Charru F. Bed load transport in turbulent flow at the grain scale: Experiments and modeling[J]. Journal of Geophysical Research: Earth Surface (2003-2012), 2010, 115(F4). |
| [5] | Radice A, Malavasi S, Ballio F. Solid transport measurements through image processing[J]. Experiments in Fluids, 2006, 41(5): 721–734. DOI:10.1007/s00348-006-0195-9 |
| [6] | Nikora V, Habersack H, Huber T, et al. On bed particle diffusion in gravel bed flows under weak bed load transport[J]. Water Resources Research, 2002, 38(6): 17–1. |
| [7] | Radice A, Ballio F. Coherent particle motion in bed load[C]//Proceedings of the First Congress of the European Section of IAHR,2010. |
| [8] | Drake T G, Shreve R L, Dietrich W E, et al. Bedload transport of fine gravel observed by motion-picture photography[J]. Journal of Fluid Mechanics, 1988, 192: 193–217. DOI:10.1017/S0022112088001831 |
| [9] | Séchet P, Le Guennec B. Bursting phenomenon and incipient motion of solid particles in bed-load transport[J]. Journal of Hydraulic Research, 1999, 37(5): 683–696. DOI:10.1080/00221689909498523 |
| [10] | Frey P, Ducottet C, Jay J. Fluctuations of bed load solid discharge and grain size distribution on steep slopes with image analysis[J]. Experiments in Fluids, 2003, 35(6): 589–597. DOI:10.1007/s00348-003-0707-9 |
| [11] | Keshavarzy A, Ball J E. An application of image processing in the study of sediment motion[J]. Journal of Hydraulic Research, 1999, 37(4): 559–576. |
| [12] | Papanicolaou A N, Diplas P, Balakrishnan M, et al. Computer vision technique for tracking bed load movement[J]. Journal of Computing in Civil Engineering, 1999, 13(2): 71–79. DOI:10.1061/(ASCE)0887-3801(1999)13:2(71) |
| [13] | Zimmermann A E, Church M, Hassan M A. Video-based gravel transport measurements with a flume mounted light table[J]. Earth Surface Processes and Landforms, 2008, 33(14): 2285–2296. DOI:10.1002/esp.1675 |
| [14] | Smith B T, Ettema R. Flow resistance in ice-covered alluvial channels[J]. Journal of Hydraulic Engineering, 1997, 123(7): 592–599. DOI:10.1061/(ASCE)0733-9429(1997)123:7(592) |
| [15] | Cao Z, Pender G, Meng J. Explicit formulation of the Shields diagram for incipient motion of sediment[J]. Journal of Hydraulic Engineering, 2006, 132(10): 1097–1099. DOI:10.1061/(ASCE)0733-9429(2006)132:10(1097) |
| [16] | Zhong Q, Li D, Chen Q, et al. Coherent structures and their interactions in smooth open channel flows[J]. Environmental Fluid Mechanics, 2015, 15(3): 653–672. DOI:10.1007/s10652-014-9390-z |
| [17] | Einstein H A, El-Samni E S A. Hydrodynamic forces on a rough wall[J]. Reviews of Modern Physics, 1949, 21(3): 520–524. DOI:10.1103/RevModPhys.21.520 |
| [18] | 苗蔚, 陈启刚, 李丹勋, 等. 泥沙起动概率的高速摄影测量方法[J]. 水科学进展, 2015, 05: 1–10. Miao W, Chen Q G, Li D X, et al. Imaging-based measurement of pickup probability for sediment entrainment[J]. Advances in Water Science, 2015, 05: 1–10. DOI:10.1007/s13201-014-0163-0 |
| [19] | 李丹勋, 曲兆松, 禹明忠, 等. 粒子示踪测速技术原理与应用[M]. 北京: 科学出版社, 2012. Li D X, Qu Z S, Yu M Z, et al. Particle tracking velocimetry: principles and applications[M]. Beijing: Science Press, 2012. |
| [20] | Armanini A, Cavedon V, Righetti M. A probabilistic/deterministic approach for the prediction of the sediment transport rate[J]. Advances in Water Resources, 2015, 81: 10–18. DOI:10.1016/j.advwatres.2014.09.008 |
| [21] | Einstein H A. The bed-load function for sediment transportation in open channel flows[M]. , 1950. |



