2. 中国空气动力研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
由于风洞自由飞试验数据采集的特殊性,即测量数据只包含模型位置和姿态角信息,无法获取线加速度、角速率及角加速度的测量量[1],导致气动力系数的辨识准度受位置信息等测量精度影响很大[2],故待估气动参数的散布较大,正确评价待估参数的辨识准度十分重要。目前,广泛采用Cramér-Rao界作为参数估计准度的度量,但通常情况下,Cramér-Rao界过于乐观[3-4]。文献[4]的方法通过对残差进行频谱分析来对Cramér-Rao界进行修正,这需要分析者工程经验十足,且工作量较大。文献[5]首先提出一种方法来处理传统的最大似然估计残差,以便计算出有色残差情况下精确的Cramér-Rao下界,并将其应用于F-18飞行器的纵向机动飞行中[6]。针对风洞自由飞试验中测量数据被有色噪声污染的实际情况,本文采用一种新的修正协方差方法替代传统方法计算Cramér-Rao界,通过对多次Monte Carlo仿真试验和风洞试验实测数据进行气动参数辨识结果的准度评价,验证了修正协方差方法计算Cramér-Rao界的有效性,其客观反映了参数辨识结果的精准度。
1 气动参数辨识准度评价方法 1.1 气动参数辨识原理目前工程上应用最为广泛的气动力参数辨识方法是最大似然法(MLE:Maximum Likelihood Estimation),该方法将参数辨识问题转化为一优化问题,通过优化选取气动力模型参数值,使模型输出与实测值间的偏差达极小[7],其形式如下[8]:
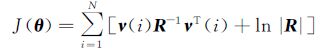 (1)
(1)
式中:ν(i)为输出误差向量:
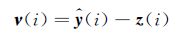 (2)
(2)
式中: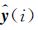
 (3)
(3)
气动参数辨识问题就是寻求待辨识参数θ的最大似然估计值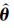
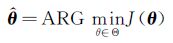 (4)
(4)
本文采用修正Newton-Raphson迭代算法求解此优化问题。其迭代公式为:
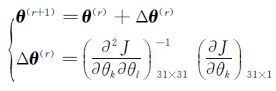 (5)
(5)
式中:
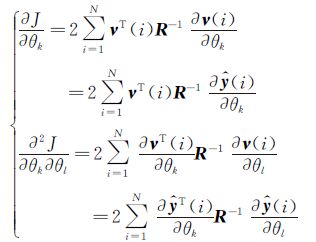 (6)
(6)
其中,定义灵敏度矩阵S,表示观测量对待辨识参数的灵敏度,其表达式为:
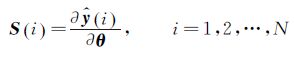 (7)
(7)
Cramér-Rao不等式是准度估计理论中最重要的结果,它给出参数估计准度可达到的理论极限。在某种意义上,Cramér-Rao不等式给出了数据中所含信息量的度量。对于有偏估计,Cramér-Rao不等式为:
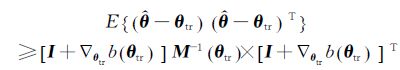 (8)
(8)
式中:▽θtrb(θtr)表示估计的偏差对参数真值的一阶梯度,M为信息矩阵。
对于无偏估计,b(θtr)=0,式(8)化为:
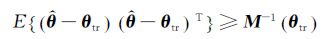 (9)
(9)
式(9)表明,参数估计值与真值的方差总是大于信息矩阵之逆,只有当信息矩阵无穷大时,才能充分接近真值,即当试验的数据足够多时,式(9)的等式成立。经验证明,只要数据含有系统的最大固有周期的几倍长的数据,式(9)的等号就接近成立[9-11]。因此式(9)是最大似然参数估计准度的最好度量。在参数估计时,θtr是未知的,故以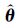
对于飞行器动力学系统模型,当过程噪声分布矩阵为零,观测噪声分布矩阵已知时,信息矩阵M的表达式为:
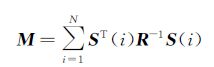 (10)
(10)
定义信息矩阵M的逆矩阵为散布矩阵D:
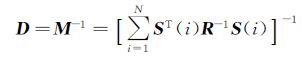 (11)
(11)
那么,矩阵D的对角线元素djj给出第j个参数估计值方差的下界,Cramér-Rao不等式及Cramér-Rao下界表达式为:
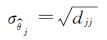 (13)
(13)
Cramér-Rao界是预测准度的方法,这已被气动参数辨识的大量数字仿真所证实。但是对于飞行试验实测数据的参数辨识实践却表明,重复多次飞行试验所得参数估计结果的标准差比Cramér-Rao界高5~10倍[12-14]。原因在于,采用式(13)估算Cramér-Rao界时,假定了系统噪声是平均分布于直至Nyquist频率的白噪声,而对气动参数辨识有重要影响的噪声却是局限于低频区域的有色噪声。噪声特性的差异导致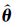
在有色测量噪声下,参数估计的协方差为[15]:
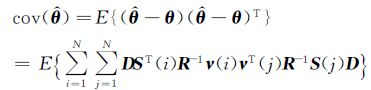 (14)
(14)
当最大似然估计算法收敛时,离散噪声协方差阵和观测灵敏度独立于参数估计,于是上式可改写为:
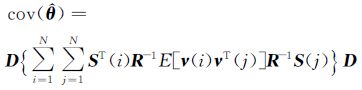 (15)
(15)
对于有色残差,有:
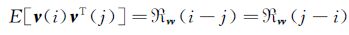 (16)
(16)
式中:Rνν(i-j)为输出残差的自相关函数[16]。其无偏估计为:
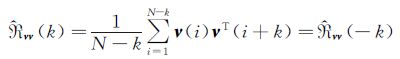 (17)
(17)
将式(16)代入式(15),得:
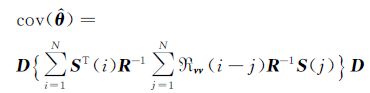 (18)
(18)
式(18)给出了有色测量噪声情况下参数估计的协方差阵,其中,Rνν(i-j)和R均采用式(17)进行估计。
参数估计的标准差为:
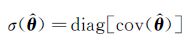 (19)
(19)
本节以某10°半锥角尖锥模型为例,具体说明气动参数辨识算法在高超声速风洞自由飞试验中的应用。模型及试验工况的基本参数为:m=0.2217kg,l=0.168 96m,底部直径D=0.06m,总压p0=514 520Pa,总温T0=410K,来流马赫数Ma=5,采样频率f=2000Hz。给定模型仿真初始条件:V=7m/s、θ=5°、ψ=5°、γ=0°和1组气动参数,在6个观测量上添加白噪声,其中,位置坐标、俯仰角、偏航角和滚转角的噪声标准差分别为1mm、0.1°、0.1°和0.02°。进行300次Monte Carlo仿真试验,采用最大似然法对其进行气动参数辨识,待辨识参数为。
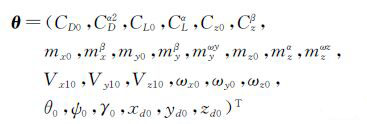 (20)
(20)
表 1列出了Monte Carlo试验气动参数估计的统计结果,文中涉及到的角度单位以弧度计。表 1中,第2列“真值”为仿真时所用参数值,第3~4列为300次试验的参数估计值的均值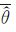
|
气动 参数 | 真值 | 估计值 | 传统 | 修正 | |||
| $\overline{{\hat{\theta }}}$ | s | σ | s/σ | σc | s/σc | ||
| CD0 | 0.13500 | 0.13500 | 0.00022 | 0.00021 | 1.06 | 0.00013 | 1.69 |
| CDα2 | 2.57020 | 2.56932 | 0.02244 | 0.02126 | 1.06 | 0.01385 | 1.62 |
| CLα | 2.15624 | 2.15877 | 0.06208 | 0.06107 | 1.02 | 0.04049 | 1.53 |
| Czβ | -2.15624 | -2.15587 | 0.04092 | 0.04191 | 0.98 | 0.03054 | 1.34 |
| mxβ | -0.01000 | -0.01000 | 0.00002 | 0.00001 | 1.07 | 0.00001 | 1.69 |
| myβ | -0.16616 | -0.16616 | 0.00002 | 0.00002 | 1.00 | 0.00001 | 1.91 |
| myωy | -0.50000 | -0.49994 | 0.00150 | 0.00141 | 1.06 | 0.00088 | 1.70 |
| mzα | -0.16616 | -0.16616 | 0.00003 | 0.00003 | 1.00 | 0.00002 | 1.77 |
| mzωz | -0.50000 | -0.49999 | 0.00246 | 0.00238 | 1.04 | 0.00144 | 1.71 |
由表 1可见,参数估计的统计标准差s与Cramér-Rao界方法、修正协方差方法给出的标准差均值一致。结果表明,在测量噪声为白噪声情况下,2种方法均较好地反映了辨识结果的分布,均可以作为参数估计准度的有效度量。
2.2 有色噪声对辨识结果的影响由于对气动参数辨识有重要影响的噪声主要是低频区域的有色噪声,故在6个观测量上添加不同水平的有色噪声。下面简要介绍以气动参数辨识为目的添加的有色测量噪声的生成过程。由于高超声速风洞自由飞试验空间较小,试验时间较短等固有特点,故本文采用的轴对称尖锥模型的纵向短周期运动为主要运动模态,有色噪声的主要功率谱应分布于[0,ωn]上,大于Nyquist频率的区间上功率谱为0,其余部分采用高斯白噪声描述。ωn为纵向短周期模态近似频率[17],表达式如下:
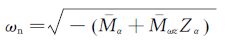 (21)
(21)
式中:
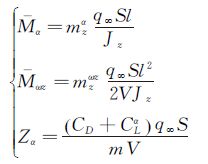 (22)
(22)
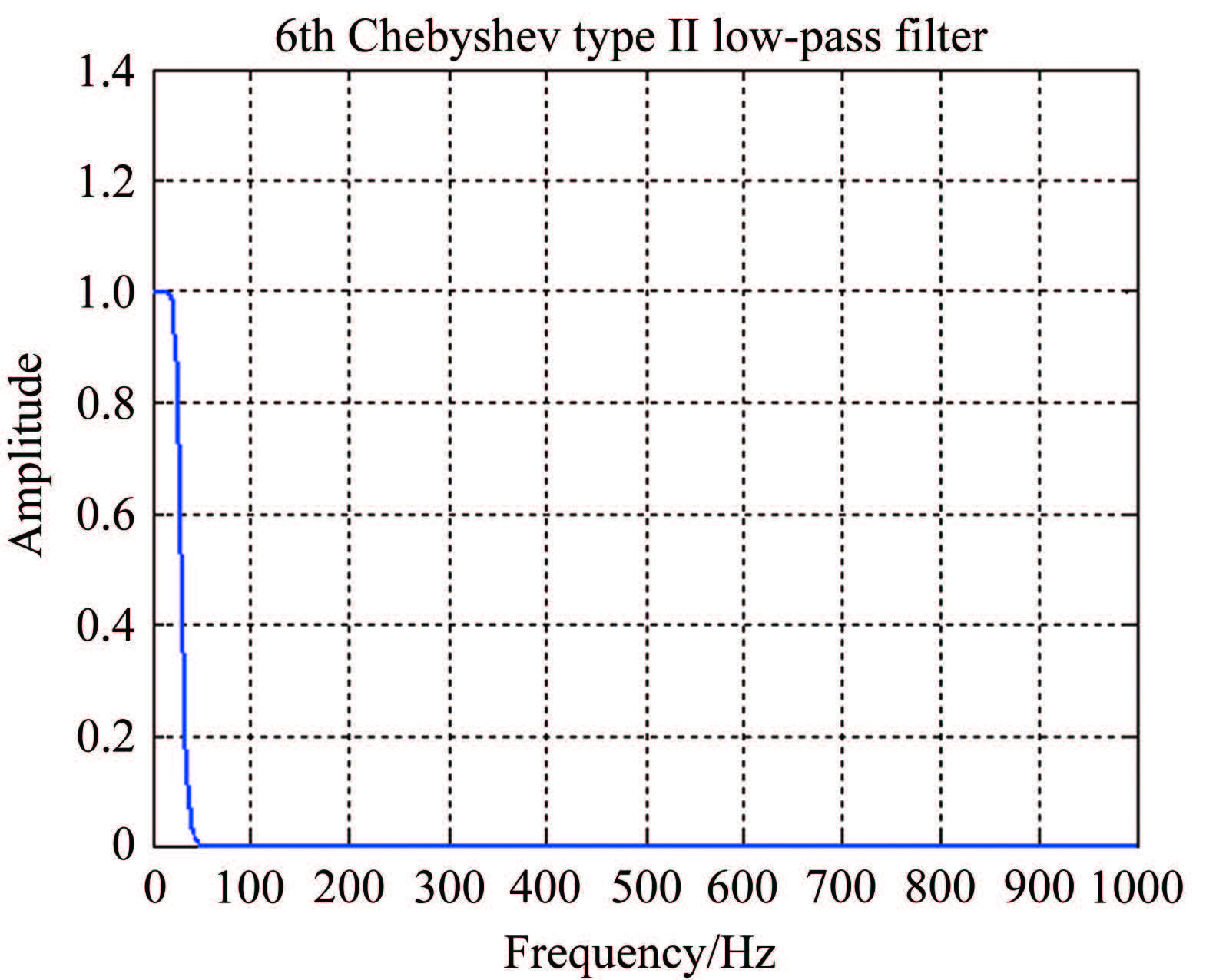
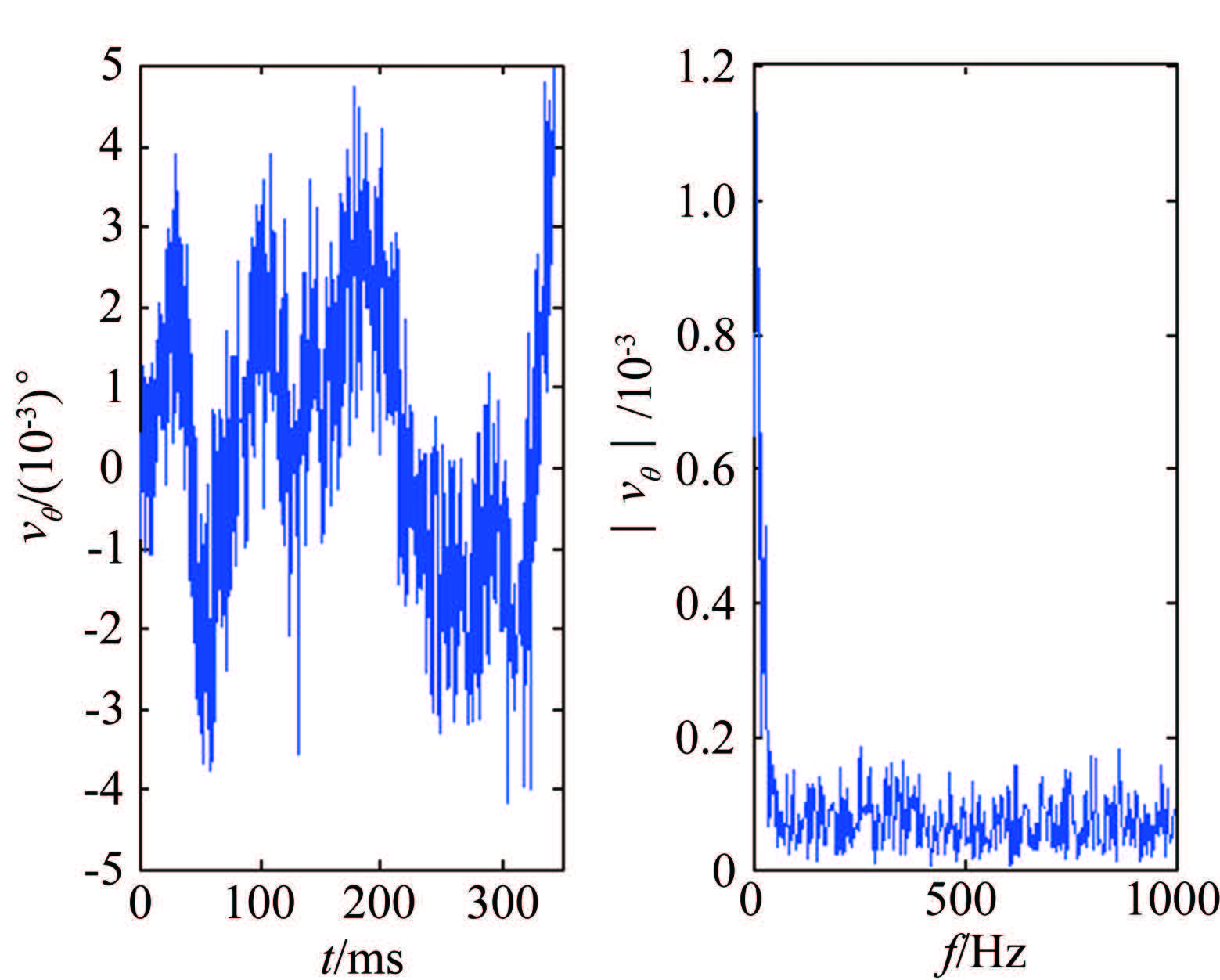
根据式(21)计算得出ωn约为25Hz。有色噪声的窄带部分先由零均值高斯白噪声通过一个如图 1所示的通带边界频率为25Hz、阻带截止频率为50Hz的6阶Chebyshev II型低通滤波器生成,再与一个独立的宽带零均值高斯白噪声相叠加。通过对噪声幅值进行调节,达到所需信噪比。在进行Monte Carlo仿真时,对所有仿真输出量均采用此种方式独立地添加噪声。图 2给出了第300次仿真中叠加到θ上的有色噪声时间序列和频谱图。采用此种方法生成的有色噪声较好地模拟了真实飞行试验数据残差序列的特点,这也是本文采用此有色噪声模型的原因所在。
|
| 图 1 6阶Chebyshev II型低通滤波器 Fig.1 Sixth-order Chebyshev type II low-pass filter |
|
| 图 2 有色噪声时间历程和频谱图(θ,RUN=300) Fig.2 Time history curve and power spectrum of example simulated colored noise (θ,RUN=300) |
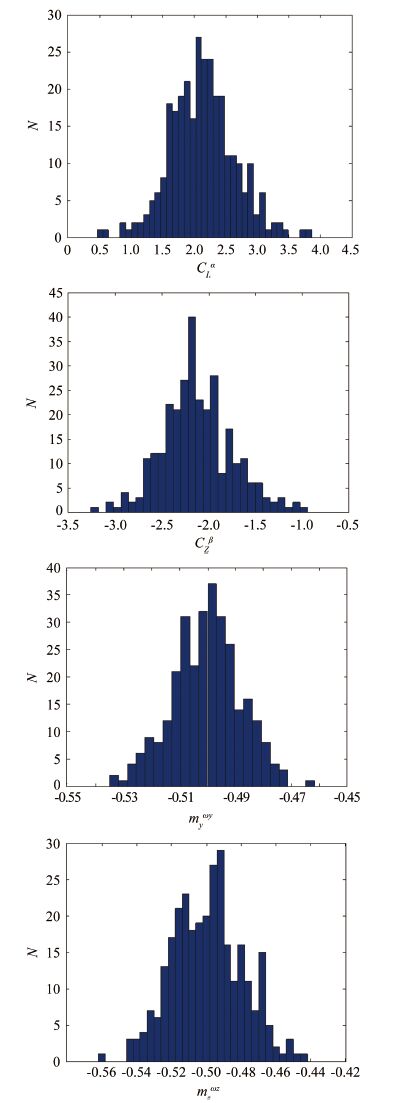
在6个观测量上添加上文所述形式的有色噪声,噪声水平与2.1节白噪声水平一致,进行300次Monte Carlo仿真试验,并对其进行参数辨识。图 3示出了CLα、Czβ、myωy和mzωz的估计结果分布,可见对于最大似然估计,当试验次数足够多时,参数估计值的概率分布趋近于以真值为中心的高斯正态分布。
|
| 图 3 Monte Carlo仿真试验的参数估计值分布图 Fig.3 Aerodynamic parameter estimation results from Monte Carlo simulation |
表 2列出了Monte Carlo试验气动参数估计的统计结果。由表 2可见,参数估计的统计标准差s约为传统的Cramér-Rao界方法给出的标准差均值σ-的5倍,表明传统的Cramér-Rao界方法过于乐观。而参数估计的统计标准差s与修正协方差方法给出的标准差均值σc大致相当,表明修正协方差方法较为合理,可以作为参数估计准度的度量。
|
气动 参数 | 真值 | 估计值 | 传统 | 修正 | |||
| $\overline{{\hat{\theta }}}$ | s | σ | s/σ | σc | s/σc | ||
| CD0 | 0.13500 | 0.13485 | 0.00185 | 0.00034 | 5.52 | 0.00102 | 1.83 |
| CDα2 | 2.57020 | 2.58595 | 0.17831 | 0.03430 | 5.20 | 0.10691 | 1.67 |
| CLα | 2.15624 | 2.13110 | 0.51014 | 0.10124 | 5.04 | 0.35518 | 1.44 |
| Czβ | -2.15624 | -2.11901 | 0.37293 | 0.07006 | 5.32 | 0.24308 | 1.53 |
| mxβ | -0.01000 | -0.01001 | 0.00012 | 0.00002 | 4.94 | 0.00008 | 1.53 |
| myβ | -0.16616 | -0.16616 | 0.00014 | 0.00003 | 5.34 | 0.00006 | 2.32 |
| myωy | -0.50000 | -0.50028 | 0.01210 | 0.00230 | 5.26 | 0.00666 | 1.82 |
| mzα | -0.16616 | -0.16616 | 0.00024 | 0.00005 | 4.75 | 0.00012 | 2.03 |
| mzωz | -0.50000 | -0.49938 | 0.01999 | 0.00390 | 5.13 | 0.01140 | 1.75 |
上文中仿真算例是将各观测量的仿真时间历程作为实测值,即使对仿真值叠加白噪声或有色噪声,也并不能完全反映真实试验飞行历程,所以本节针对10°半锥角尖锥模型的风洞自由飞试验实测数据开展气动参数辨识研究。
试验是在中国空气动力研究与发展中心超高速空气动力研究所Φ1m高超声速风洞中进行的。共进行5次试验,试验模型构型及工况与2.1节近似,各具体参数如表 3所示。观测量与待辨识气动参数的选取与2.1节一致,主要气动参数的估计结果及其Cramér-Rao界如表 4和图 4所示。图 4中符号“○”表 示参数估计值,分别将采用传统方法和修正协方差方法计算的待估参数的标准差σ和σc作为误差带,以红色(左侧)和蓝色(右侧)实线表示。
| 参数 | 1 | 2 | 3 | 4 | 5 |
| m/kg | 0.2215 | 0.2217 | 0.2222 | 0.2215 | 0.2210 |
| l/m | 0.16918 | 0.16896 | 0.16932 | 0.16908 | 0.16922 |
| D/m | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 |
| 质心位置 | 0.597 | 0.596 | 0.596 | 0.600 | 0.600 |
| Jx/(10-5kg·m2) | 2.696 | 2.777 | 2.547 | 2.561 | 2.622 |
| Jy/(10-5kg·m2) | 6.685 | 6.489 | 6.889 | 6.476 | 6.513 |
| Jz/(10-5kg·m2) | 6.685 | 6.489 | 6.889 | 6.476 | 6.513 |
| Jxy/(10-5kg·m2) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| p0/Pa | 518010 | 514520 | 510070 | 511870 | 521640 |
| T0/K | 410 | 410 | 400 | 400 | 400 |
|
气动 参数 | 估计值 | 传统 | 修正 | |||
| $\overline{{\hat{\theta }}}$ | s | σ | s/σ | σc | s/σc | |
| CD0 | 0.16390 | 0.03828 | 0.00587 | 6.52 | 0.01968 | 1.95 |
| CDα2 | 1.00599 | 4.92853 | 0.89312 | 5.52 | 3.36375 | 1.47 |
| CLα | 2.76598 | 2.28743 | 0.15281 | 14.97 | 0.87767 | 2.61 |
| Czβ | 1.70980 | 2.54756 | 0.11755 | 21.67 | 0.60956 | 4.18 |
| mxβ | 0.00645 | 0.01744 | 0.00360 | 4.84 | 0.01135 | 1.54 |
| myβ | -0.19268 | 0.00972 | 0.00101 | 9.62 | 0.00269 | 3.61 |
| myωy | -0.71302 | 0.31171 | 0.06064 | 5.14 | 0.17015 | 1.83 |
| mzα | -0.18509 | 0.01369 | 0.00049 | 28.07 | 0.00170 | 8.06 |
| mzωz | -0.26206 | 0.36579 | 0.03127 | 11.70 | 0.11581 | 3.16 |
由图 4可见,各参数采用修正协方差方法计算的标准差σc远大于传统方法计算结果σ,说明采用传统方法计算的Cramér-Rao界过于乐观。图 4中,CDα2、CLα和CZβ的散布较大,相应地,表 4中对应气动参数的标准差亦很大,这是由力系数对位置坐标的测量准度十分敏感造成的,与文献[18]中的计算结果一致。实际上,由于力矩导数主要影响短周期运动,力导数影响长周期运动[19],而风洞自由飞试验的空间较小,试验时间较短,长周期运动体现不充分,位置坐标随迎角、侧滑角的变化不明显,因此,力导数的辨识存在一定难度。只有在模型上安装过载测量设备的情况下,风洞自由飞试验才能对力导数进行有效辨识。

|
| 图 4 5次风洞试验主要气动参数辨识结果 Fig.4 Aerodynamic parameter estimation results from 5 wind tunnel free-flight tests |
由图 4可见,第3、4次风洞试验中,动导数mzωz的辨识结果均大于0,与文献[18]中近似解析解和近似牛顿解不符。造成的原因可能是流场中产生不稳定绕流,使气动参数发散,进而产生动不稳定锥运动,俯仰阻尼导数mzωz的估计值大于0,这种简单细长锥体在小迎角情况下可能会产生锥动失稳的现象,与文献[20-22]一致。因此,在进行辨识结果的统计计算时,不予采纳。则第1、2和5次风洞试验得到的动导数mzωz的估计结果为: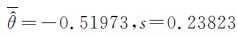
从表 4可见,采用传统方法计算的Cramér-Rao界过于乐观,远小于由5次飞行试验得到的待估气动参数的标准差,而采用修正协方差方法计算的Cramér-Rao界是传统方法计算结果的3~5倍,且与5次飞行试验得到参数的标准差接近。因此,在测量数据被有色噪声污染情况下,采用修正协方差方法计算得到的Cramér-Rao界是待估气动参数准度的一个有效度量。
可注意到,表 4中部分气动参数采用修正协方差方法计算的Cramér-Rao界虽然优于传统方法计算结果,但仍与参数估计的统计标准差略有差别,这是由于本文中高超声速风洞自由飞试验仅进行了5次,样本量较少,且每次试验所用模型及试验工况等各项条件不可能做到完全一致造成的,故可通过增加风洞试验次数和提高样本量来修正。
4 结 论本文将基于最大似然理论的气动参数辨识方法推广应用于高超声速风洞自由飞试验中。多次Monte Carlo仿真试验和风洞实测数据的辨识结果表明:
(1) 在风洞试验测量数据被白噪声污染情况下,传统方法和修正协方差方法计算的Cramér-Rao界接近,与多次重复试验的参数估计的统计标准差一致,2种方法均较好地反映了辨识结果的散布程度,均可以作为参数估计准度的有效度量。
(2) 当试验测量数据被有色噪声污染情况下,传统方法计算的Cramér-Rao界远小于参数估计的统计标准差,将其作为参数估计准度的度量过于乐观,而采用修正协方差方法计算的Cramér-Rao界与参数估计的统计标准差十分接近,将其作为辨识参数结果的准度评价,更能准确地反映试验中待估气动参数的散布程度。
(3) 采用Chebyshev II型低通滤波器生成的有色噪声信号能量主要集中于低频段,而在高频段能量较低,此种有色噪声信号较好地仿真了真实的高超声速风洞试验测量噪声,并将其应用于Monte Carlo仿真试验中。
(4) 采用修正协方差方法的Cramér-Rao界的全部计算在时域上进行,避免了对有色残差进行频域分析,因此该方法适用范围广,对使用者的工程经验不作要求。
| [1] | 张守言. 模型自由飞试验[M]. 北京: 国防工业出版社, 2002. |
| [2] | Prislin R H. High amplitude dynamic stability characteristics of a blunt 10-degree cones[R]. AIAA-66-465, 1966. |
| [3] | Klein V. Determination of stability and control parameters of a light airplane from flight data two estimation methods[R]. NASA TP-1306, 1979. |
| [4] | Maine R E, Iliff K W. The theory and practice of estimating the accuracy of dynamic flight-determined coefficients[R]. NASA RP-1077, 1981. |
| [5] | Morelli E A, Klein V. Determining the accuracy of maximum likelihood parameter estimates with colored residuals[R]. NASA CR-194893, 1994. |
| [6] | Morelli E A, Klein V. Accuracy of aerodynamic model parameters estimated from flight test data[J]. Journal of Guidance, Control and Dynamics, 1997, 20(1): 74–80. DOI:10.2514/2.3997 |
| [7] | 蔡金狮. 飞行器系统辨识学[M]. 北京: 国防工业出版社, 2003. |
| [8] | 汪清, 钱炜祺, 何开锋. 导弹气动参数辨识与优化输入设计[J]. 宇航学报, 2008, 29(3): 789–793. Wang Q, Qian W Q, He K F. Aerodynamic parameter identification and optimal input design for missile[J]. Journal of Astrinautics, 2008, 29(3): 789–793. |
| [9] | Murphy P C. A methodology for airplane parameter estimation and confidence interval determination in nonlinear estimation problems[R]. NASA RP-1077, 1981. |
| [10] | Murphy P C, Klein V. Maximum likelihood algorithm using an efficient scheme for computing sensitivities and parameter confidence intervals[R]. AIAA-84-2084, 1984. |
| [11] | Murphy P C. Efficient computation of confidence intervals of parameters[R]. AIAA-87-2624, 1987. |
| [12] | Iliff K W, Maine R E. Further observations on maximum likelihood estimates of stability and control characteristics obtained from flight data[R]. AIAA-77-1133, 1977. |
| [13] | Maine R E, Iliff K W. Use of Cramér-Rao bounds on flight data with colored residuals[J]. Journal of Guidance, Control and Dynamics, 1981, 4(2): 207–213. DOI:10.2514/3.56073 |
| [14] | Balakrishnan A V, Maine R E. Improvements in aircraft extraction programs[R]. NASA CR-145090, 1975. |
| [15] | Morelli E A, Klein V. Determing the accuracy of aerodynamic model parameters estimated from flight test data[R]. NASA CR-203351, 1995. |
| [16] | Bendat J S, Piersol A G. Random data analysis and measurement procedures[M]. New York: Wiley, 1986. |
| [17] | 方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2005. |
| [18] | 张天姣, 钱炜祺, 何开锋, 等. 基于最大似然法的风洞自由飞试验气动力参数辨识技术研究[J]. 实验流体力学, 2015, 29(5): 8–14. Zhang T J, Qian W Q, He K F, et al. Research on aerodynamic parameter identification technology in wind tunnel free-flight test based on Maximum Likelihood Estimation[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 8–14. |
| [19] | 顾均晓. 飞行稳定性和自动控制[M]. 北京: 国防工业出版社, 2008. |
| [20] | 贾区耀, 杨益农, 陈农. 风洞自由飞实验测量M=5, 10°半锥角尖锥、钝锥气动动稳特性[J]. 空气动力学学报, 2007, 25(2): 24–28. Jia Q Y, Yang Y N, Chen N. Measurement of aerodynamic dynamic stability characters of M=5 pointed and blunted cones with semi-cone angles equal 10° in wind tunnel free flight experiment[J]. Acta Aerodynamica Sinica, 2007, 25(2): 24–28. |
| [21] | 贾区耀, 杨益农. 锥动失稳与无控飞行器弹着点精度[J]. 气动物理—理论与应用, 2007, 2(2): 183–186. Jia Q Y, Yang Y N. Conical lose of stability and unguided aircraft impact accuracy[J]. Physics of Gases: Theory and Applications, 2007, 2(2): 183–186. |
| [22] | 陈农, 杨益农, 贾区耀. 小迎角下钝锥气动动态稳定性[C]//全国第九届分离流, 旋涡和流动控制会议论文集, 2002: 74-83. |
| [23] | 马家驩, 潘文欣, 翟曼玲, 等. 10°尖锥标模高超声速动导数的实验测量[J]. 空气动力学学报, 1997, 15(4): 452–457. Ma J H, Pan W X, Zhai M L, et al. 10° Cone model free flight experiment in hypersonic impulse type wind tunnel for dynamic stability measurement[J]. Acta Aerodynamica Sinica, 1997, 15(4): 452–457. |



