边界层是自然界和工程界中典型的流动形态之一,工程技术中大量的流动问题(如失速、减阻等)和边界层密切相关[1],而边界层流动参数的准确测量是对边界层进行机理研究的基础。
对于水下平板湍流边界层而言,壁面摩擦速度的测量一直是一个难点,早期测量水下壁面摩擦速度主要使用Preston管法,该方法是将Preston管固定在湍流边界层的壁面上依据壁面律测量壁面的剪应力[2],但由于需要在壁面上插管,破坏了原有的流场结构,从而影响测量的真实性和可靠性。后来随着热线测速技术(HWA)、激光测速技术(LDV)和粒子图像测速技术(PIV)的成熟与发展[1],边界层速度剖面法成为了测量壁面摩擦速度新的选项。热线测速法的时空分辨率高,信号连续,在测量微观流场方面具有较大的优越性,但热线仪对环境温度敏感,多用在空气介质中,具体在测量水下平板边界层近壁区速度剖面时,热线仪与平板壁面之间还存在热传导效应,测量精度受到影响。LDV[3] 测量技术为单点无接触式,具有测速精度高、动态响应快、无需标定等优势,不存在热线法所面临的导热问题。相比HWA和LDV的单点测量,PIV[4-6]则能够在瞬间测出成千上万点的速度,并具有流场动态显示的能力。但PIV的分辨率相对不高(在帧率提高的情况下其分辨率还会降低),同时PIV测得的数据还存在噪声问题。因此对于水下平板边界层参数的测量使用LDV能获得更好的精度。LDV测量法[7]通常是测得近壁区的平均速度剖面,再将测得的数据进行对数律层的非线性迭代拟合求得壁面摩擦速度,但该方法存在的问题是需要在测得的数据中选取对数律层的起始点和最终点,这会给测量结果带来主观误差。Niederschulte M. A.等人[8]通过LDV测得了近壁区深入到粘性底层的速度剖面数据,并基于在粘性底层速度沿法线方向呈线性分布的假设求出速度梯度和壁面摩擦速度。但此方法需要激光控制体完全贴近壁面,以获得y+<2.5区域的速度数据,且对粘性底层速度测量的精度提出了很高的要求,而实际上由于粘性底层贴近壁面速度梯度很大,示踪粒子少,粒子在剪切层中不均匀的分布也可能会引起信号的不连续及偏差[9]。这给水下平板近壁区的速度测量带来了很大的挑战。
本文利用激光多普勒测速技术(LDV)在小型水槽中对光滑平板边界层平均速度剖面进行实验测量,通过对测得的速度数据进行从壁面到对数律层尾区的拟合获得壁面摩擦速度及相关流动参数(无需激光控制体完全贴近壁面和对对数律层的速度数据进行仔细挑选),并与经验公式和数值计算结果相比较,实验结果可用作水中MEMS壁面剪应力传感器标定的输入。
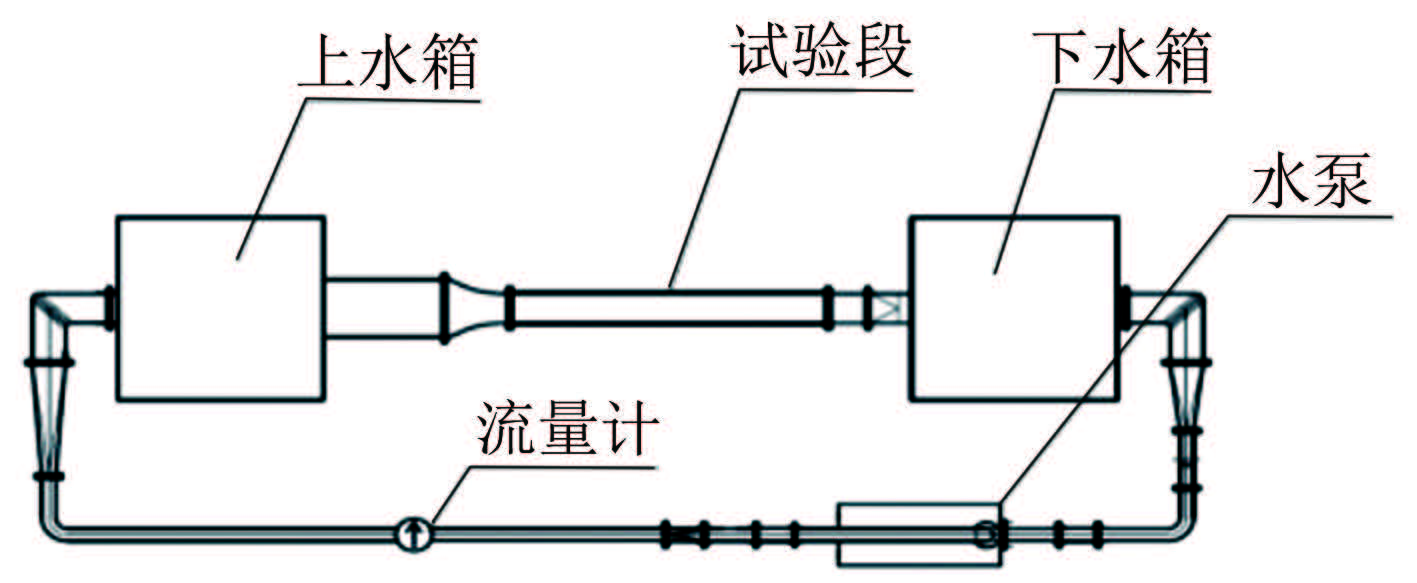
1 水下平板边界层LDV测量实验 1.1 实验设备实验在中国船舶科学研究中心(中船重工第702研究所)小型精密水槽完成,该水槽为串联回流式,结构如图 1所示。实验段为矩形槽道,尺寸为2350mm×250mm×150mm(长×宽×高)。实验段流速为0.1~1m/s无级可调,湍流度和均匀度均小于1%。
|
| 图 1 精密水槽结构示意图 Fig.1 Precision water flume structural diagram |
测速系统包括DANTEC高能版FlowExplorer系统,DANTEC高精度专用坐标架,BSA F60信号处理系统等。LDV镜头焦距为500mm,为了保证良好的光学特性和跟随性,选用示踪粒子为5μm的PSP粒子。实验过程中采用标准铂电阻温度计监测温度变化,保证其波动不超过0.5℃。
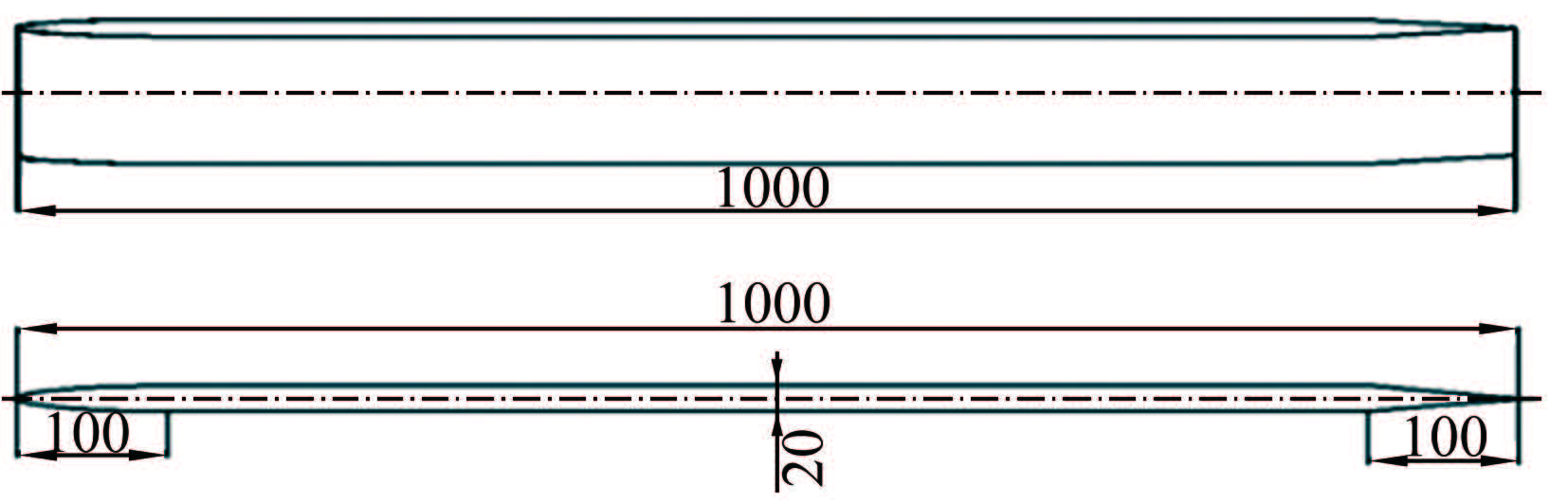
1.2 实验模型与方法实验模型为一块光滑的抗锈铝平板(板面喷有黑色亚光漆),板长1000mm,宽度150mm,厚度为20mm。平板模型的进流段设计成半椭圆状,其长短轴比为10∶1,去流段设计成对称斜面,尖削比为10∶1,平板模型尺寸如图 2所示。
|
| 图 2 平板模型示意图 Fig.2 Flat plate model diagram |
平板模型垂直安装在水槽实验段中,在进行平板速度剖面测量之前需要先进行平板沿程流速测量以检测平板的零压力梯度。沿程流速测量如图 3所示。

|
| 图 3 沿程流速测量实验照片 Fig.3 Measurement of velocity along flowing direction |
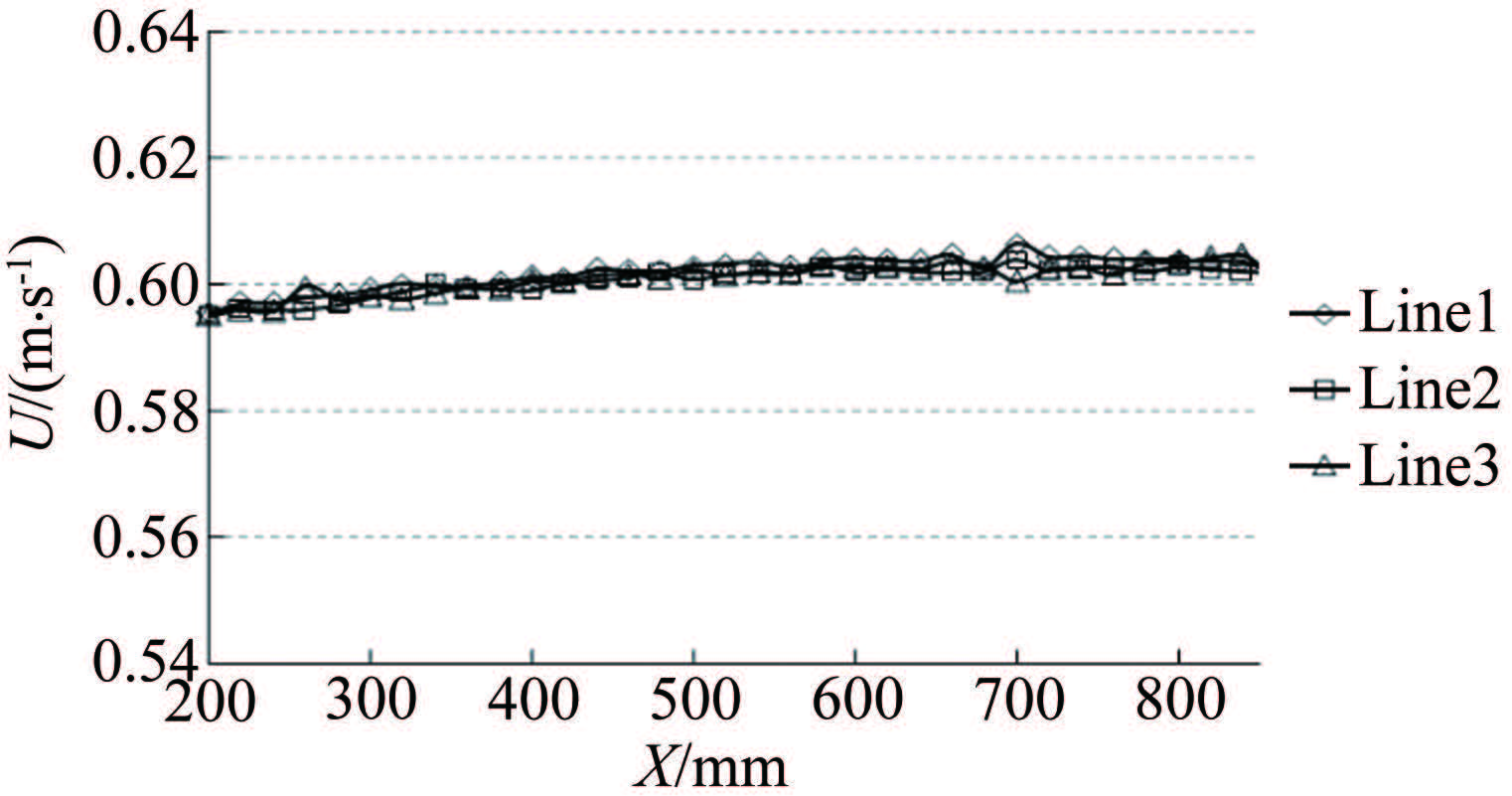
本文分别沿3条槽道中线Line1,Line2,Line3测量了外流速度(U=0.6m/s)沿流向的发展情况,这3条槽道中线距平板表面分别为65,55和45mm,每条线上相邻2个测点之间相距20mm,测量结果如图 4所示,图中横坐标表示测点距前缘的距离。
|
| 图 4 外流速度0.6m/s时的沿程流速分布 Fig.4 Velocity distribution along flowing direction (freestream velocity =0.6m/s) |
其中同一条流线上流速相对差异都在1.3%以内,不同流线差异在2%以内,表明外流速度沿流向基本没有变化,可以认为是零压力梯度。
LDV在测量流速时参数设置如下:数据率(Date Rate)为1000Hz以上,数据有效率(Validation)为90%以上,采样样本数(Samples)N为20000个。LDV的测点距离平板前缘800mm,测量速度剖面时平板外流速度为0.2~0.7m/s,间隔为0.1m/s,速度剖面测量采用LDV结合DANTEC高精度坐标架进行,测量实验照片如图 5所示。

|
| 图 5 速度剖面测量实验照片 Fig.5 Mean velocity profile measurement |
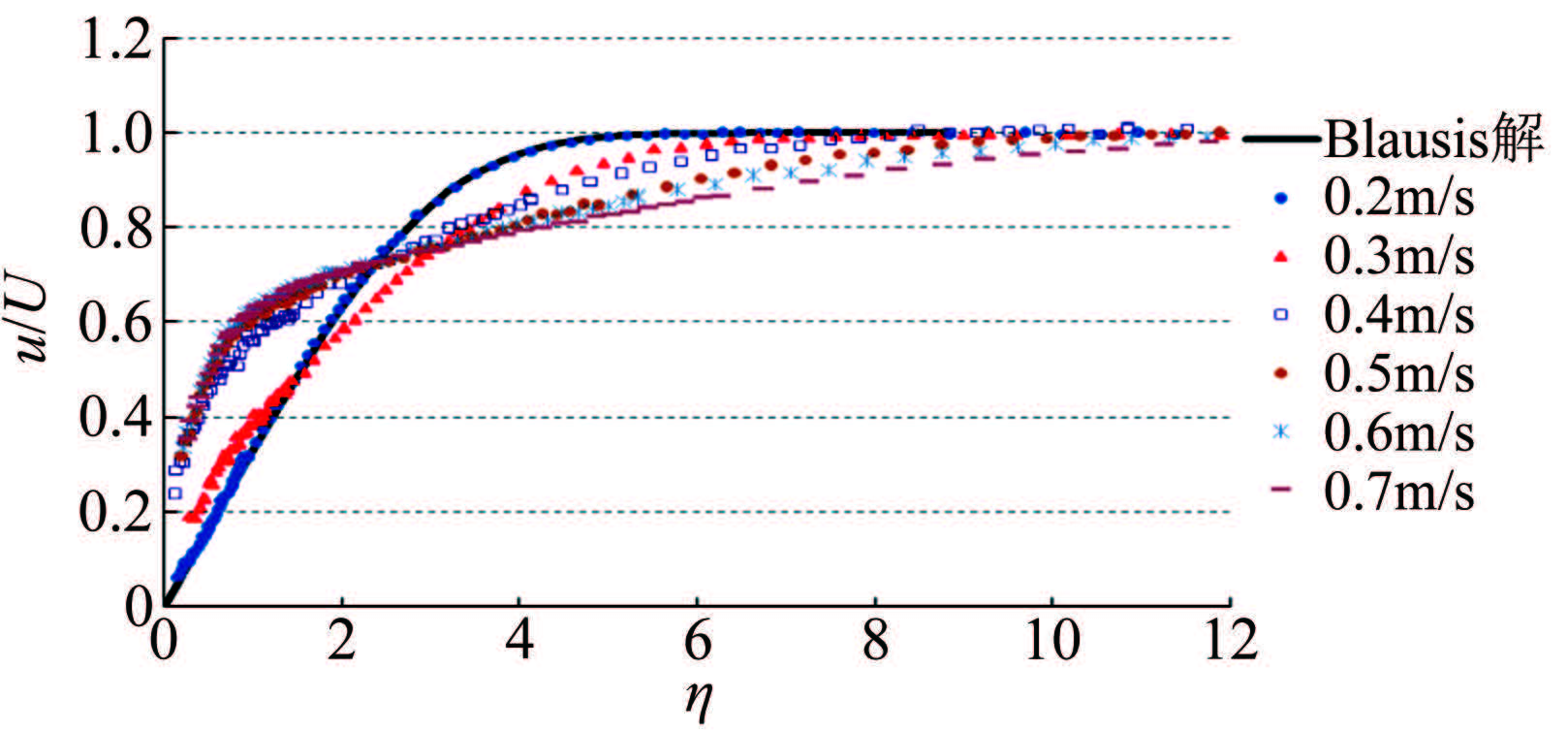
本文选取的测点为后期测量实验贴MEMS传感器区域的中间点(距平板前缘800mm),通过LDV测速系统测量不同来流速度下测点处的平均速度剖面,测量结果如图 6所示。
|
| 图 6 不同外流速度下的速度剖面 Fig.6 Mean velocity profile of different freestream velocities |
为了方便比较,图中分别对横纵坐标进行了无量纲化处理(横坐标为无量纲的高度参数η=y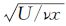
由流体力学相关理论可知,边界层厚度通常取流速由0逐渐增至自由来流速度的99%的位置处与壁面间的距离。因此边界层厚度可由速度剖面获得,相关边界层流动特性参数计算结果如表 1所示。其中δ、δ*和θ分别表示边界层厚度、位移厚度和动量厚度,H=δ*/θ为形状因子。从形状因子来看,0.2m/s的形状因子为2.58,与理想的Blasius解的形状因子2.59很接近,0.3和0.4m/s 的形状因子介于层流湍流之间,0.5~0.7m/s的形状因子接近湍流的形状因子。因此可判断0.2m/s时边界层流动为层流状态,0.3和0.4m/s时边界层流动为转捩状态,0.5~0.7m/s时边界层流动为湍流状态。
 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| δ/mm | 10.35 | 11.50 | 12.17 | 22.76 | 21.86 | 21.25 |
| δ*/mm | 3.43 | 2.32 | 1.95 | 3.06 | 2.87 | 2.79 |
| θ/mm | 1.33 | 1.24 | 1.06 | 2.11 | 2.01 | 1.96 |
| H | 2.58 | 1.98 | 1.84 | 1.45 | 1.43 | 1.42 |
当不可压缩粘性流体在零压力梯度条件下沿板面方向作湍流运动时,根据Clauser的湍流边界层理论[11],湍流边界层内的速度分布是:
壁面附近的粘性底层(0<y+<5),粘性力起主要作用,速度沿壁面法线方向呈线性分布。
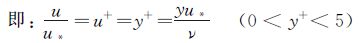 (1)
(1)
对数律层(30<y+<300),湍流切应力起主要作用,速度沿壁面法向方向呈对数律分布,湍流边界层近壁区域的对数律平均速度剖面表达式为:
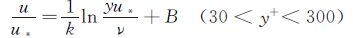 (2)
(2)
此外中间还有一个过渡层,在此层中,粘性力和湍流作用力相当,流动较复杂,很难用定律来表述,在实际应用中,因过渡层厚度极小,可直接用对数律方法处理。
由于本实验中LDV的激光控制体是一个椭球状的光斑,激光控制体无法移到平板壁面上,即不能恰好位于壁面的原点,虚拟原点y0未知。在实际的测量中由于测得的速度信息所处的无量纲位置并不能提前知道(这取决于流动雷诺数),其可能处在粘性底层、对数律层和过渡层中的任意位置上。因此不能直接将测得的实验数据与经典的边界层各子层表达式对应比较。目前确定虚拟原点和摩擦速度的方法通常是用速度剖面的对数律层公式(2)来拟合求解,但该方法的缺点是对数律层的数据起始点和最终点选择存在主观误差,同时国内外对公式(2)在低雷诺数湍流边界层下是否有效也存在争议[12],而且由于目前水槽性能所限也不能通过提高雷诺数使其达到无可争议地满足公式(2)的使用条件,因此本文采用全壁面律公式来求解虚拟原点和摩擦速度。
湍流边界层各个子层都有各自独立的表达式,对此,Spalding经过研究给出了一个全壁面律的速度分布式,见式(3):
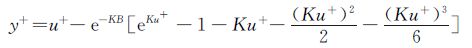 (3)
(3)
其中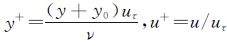
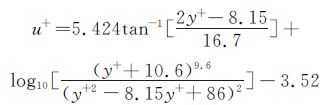 (4)
(4)
该公式0≤y+≤40的范围内与Spalding公式及经典实验数据符合较好,但随着y+继续增大误差增加很快,达到5%以上。国内学者崔杰[14]在前人的基础上推导出了Spalding公式的显式,见式(5):
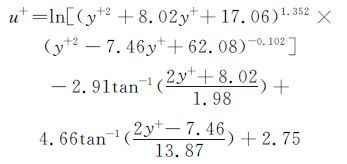 (5)
(5)
式(5)与Spalding公式(3)在0≤y+≤350误差小于0.5%,从应用角度来说,能很好地替代Spalding公式,所以本文使用式(5)来求取u*和y0。
对上面的公式(5)进行整理,可以得函数关系式
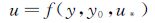 (6)
(6)
u为Spalding公式拟合得到的平均速度,y为测量点垂直方向的坐标,ν为水的运动粘性系数,y0和u*为待求参数。
壁面摩擦速度与剪应力的关系:
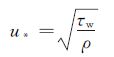 (7)
(7)
设置偏差函数[15]:
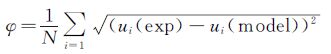 (8)
(8)
偏差函数中的实验数据为湍流边界层内层(取y+≤300,从壁面到对数律层尾区)的测量数据,将其代入偏差函数中,通过求解偏差函数φ的最小二乘解得到y0和u*值。最后用求得的壁面摩擦速度u*求解出壁面剪应力τw。
2.4 结果分析比较由于外流速度为0.5~0.7m/s时,平板测点处处于湍流流动状态,因此本文选取0.5~0.7m/s的实验数据进行湍流速度剖面Spalding公式拟合求解得到τw。为了验证LDV测量边界层参数的准确性,本文将由速度剖面得到的剪切应力与经验公式计算结果进行了比较。结果如表 2所示。
 | 0.5 | 0.6 | 0.7 |
| u* | 0.0233 | 0.0276 | 0.0321 |
| y0/mm | 0.26 | 0.26 | 0.25 |
| τw/Pa (LDV速度剖面) | 0.5419 | 0.7632 | 1.0313 |
| τw/Pa(经验公式) | 0.5463 | 0.7610 | 1.0058 |
在进行经验公式计算时,由于本文的平板模型存在椭圆头前端,当地雷诺数Rex中的下游距离x较难确定,因此这里使用基于边界层厚度的雷诺数Reδ来代替Rex。在湍流边界层中Reδ和Rex有如下关系[16]:
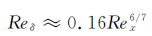 (9)
(9)
Prandtl摩擦阻力系数经验公式:
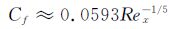 (10)
(10)
式中,Reδ=U×δx/ν,δx为测点处的边界层厚度(m),见表 1中0.5~0.7m/s对应的δ,U为外流速度(m/s),ν为运动粘性系数(m2/s)。
剪切应力与摩擦阻力系数的关系:
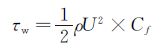 (11)
(11)
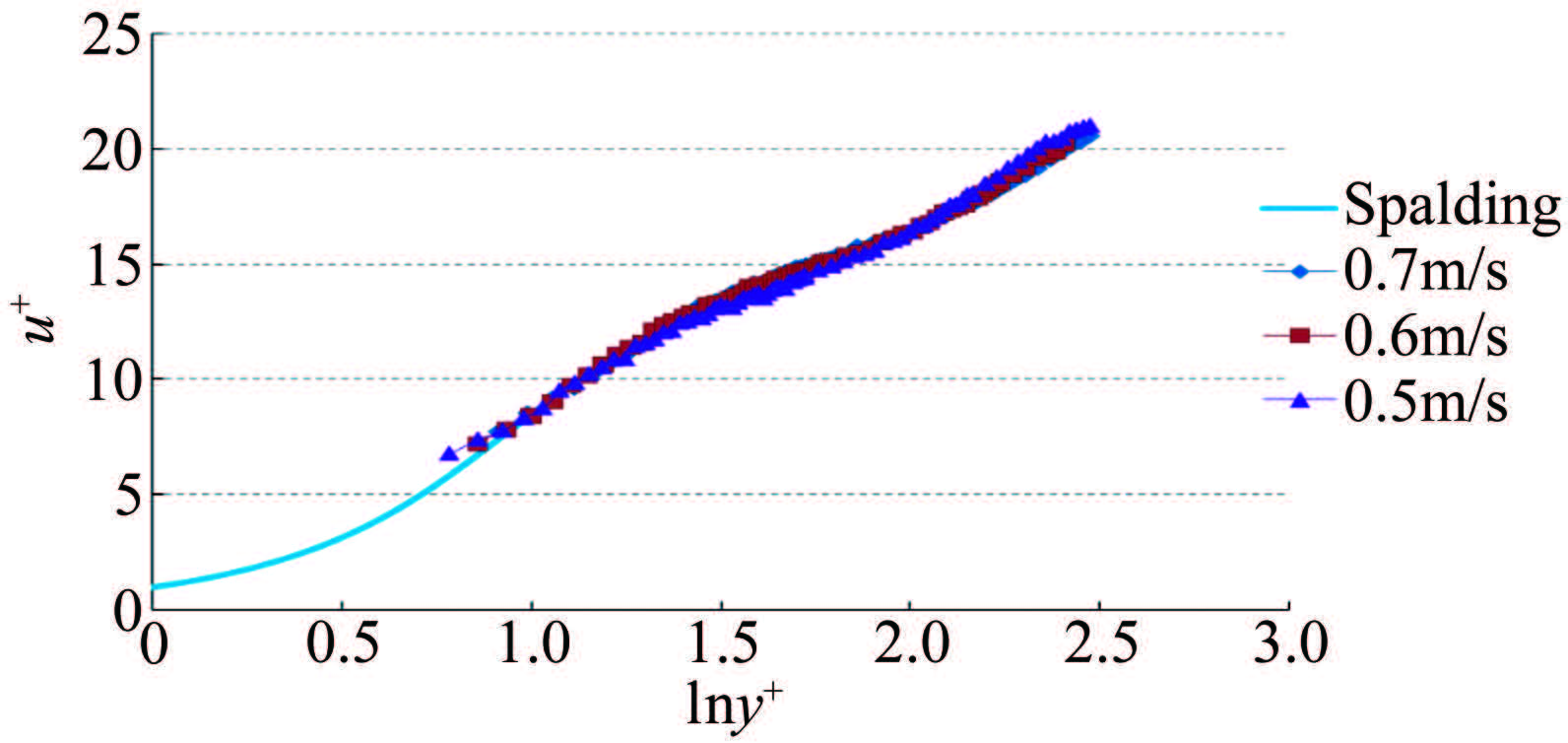
利用求得的虚拟原点及壁面摩擦速度u*,可以将测量数据无量纲化。图 7为0.5~0.7m/s无量纲化后与Spalding经验公式的比较图。
|
| 图 7 实验值与Spalding经验公式结果对比 Fig.7 Comparison of Spalding empirical formula and measured results |
从图 7中可以看出,0.5~0.7m/s的速度剖面与Spalding公式吻合较好(在y+<10的区域,由于靠近壁面区粒子较少且分布会不均匀,与Spalding公式的偏差稍大,但落在此区域的数据点非常少,对全壁面律拟合的结果影响很小,可以忽略),进一步证实其为充分发展的湍流状态。从表 2和图 7中可以看出使用LDV测速度剖面求壁面剪应力具有较好的精度,可以为MEMS传感器标定提供理想的输入。
3 数值计算 3.1 控制方程不可压缩流动控制方程包括连续性方程和雷诺平均N-S方程:
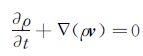 (12)
(12)
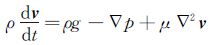 (13)
(13)
式中:v是速度矢量,p、g、ρ、μ分别为压强、重力加速度、密度、动力粘性系数。
3.2 湍流模型湍流模型选用RNG k-ε模型,在RNG k-ε模型中,通过大尺度运动和粘性项修正来体现小尺度的影响,从而使这些小尺度运动有系统地从控制方程中去除。RNG k-ε模型通过修正湍动粘度,考虑了平均流动中的旋转及旋流流动情况,可以更好地处理高应变率及流线弯曲程度较大的流动[17]。
3.3 边界条件和求解参数设置(1) 进口和出口分别为速度入口和压力出口边界条件,壁面采用无滑移边界条件,流动对称面设置为对称边界条件。残差设置为1e-6以下不再变化为收敛。
(2) 动量方程采用二阶迎风差分格式,压力速度耦合方法选用SIMPLE算法。
3.4 物理模型与网格划分(1) 物理模型
计算模拟的物理模型为图 8中所示的水下平板绕流模型,考虑到节省计算资源和绕流平板流场的对称性,本文仅对平板绕流流场的一半进行数值计算,计算域宽度为实验段宽度的一半,计算域长度和高度与实验段保持一致。

|
| 图 8 物理模型示意图 Fig.8 Computational model diagram |
(2) 网格划分
本次数值计算网格为结构化网格,总网格数为40万左右,计算网格及边界条件设置如图 9所示。计算时y+取30,第1层网格由经验公式[18]估算可得:
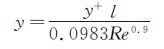 (14)
(14)
式中,l为平板长度(m);Re=U×l/ν,U为来流速度(m/s),ν为运动粘性系数(m2/s)。
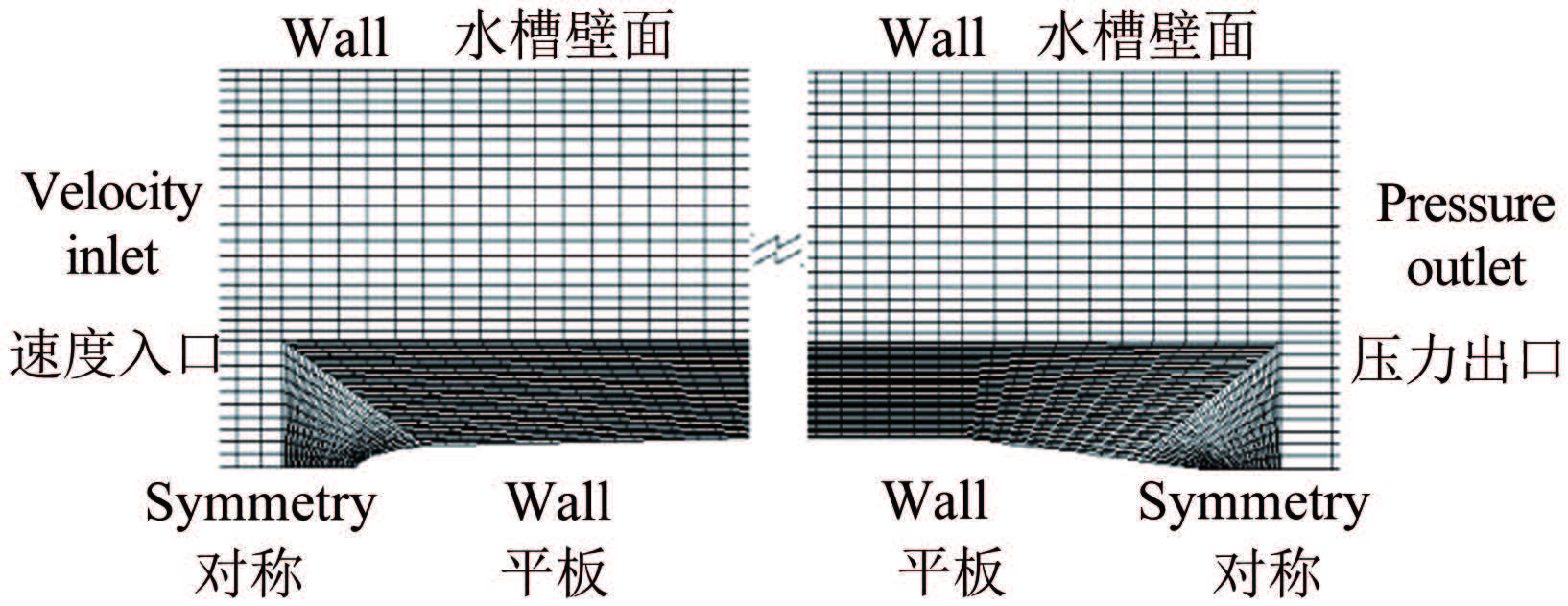
|
| 图 9 计算网格与边界条件类型 Fig.9 Computation mesh and boundary condition |
对外流速度为0.7 m/s的平板流动进行数值仿真,计算得到的平均速度剖面图和平板表面剪应力云图如图 10和11所示。从图 10可以看出,CFD计算速度剖面与LDV实验速度剖面曲线符合较好,说明CFD计算结果可对流动参数进行准确预估。从图 11可以看出,平板壁面剪应力由前端往后不断降低。在平板的去流段,截面沿流动方向持续变大,造成流动与边界分离。相应地,引起平板去流段壁面剪应力发生不规则变化。
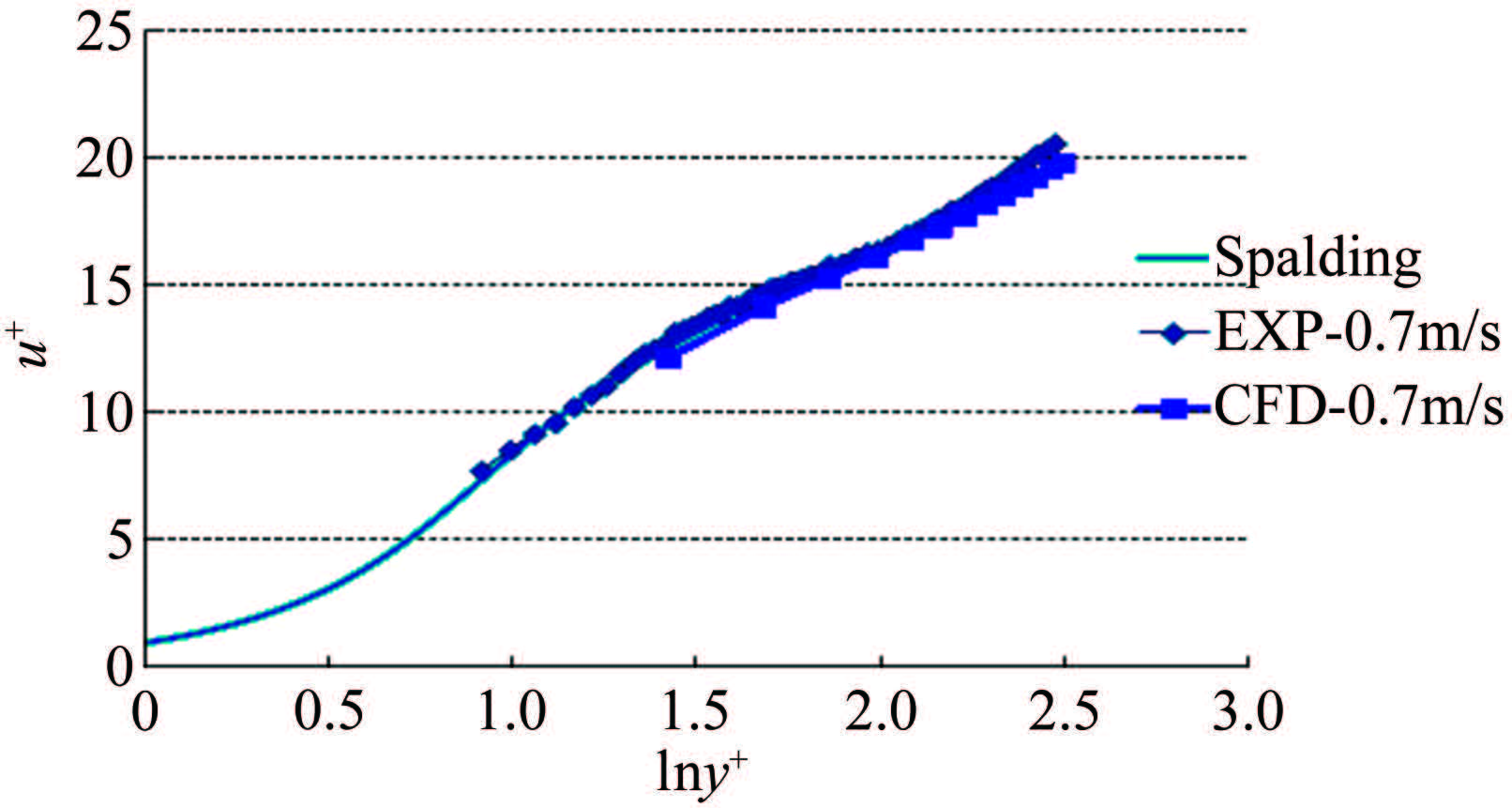
|
| 图 10 v=0.7m/s平板平均速度剖面图 Fig.10 Dimensionless velocity profile(v=0.7m/s) |
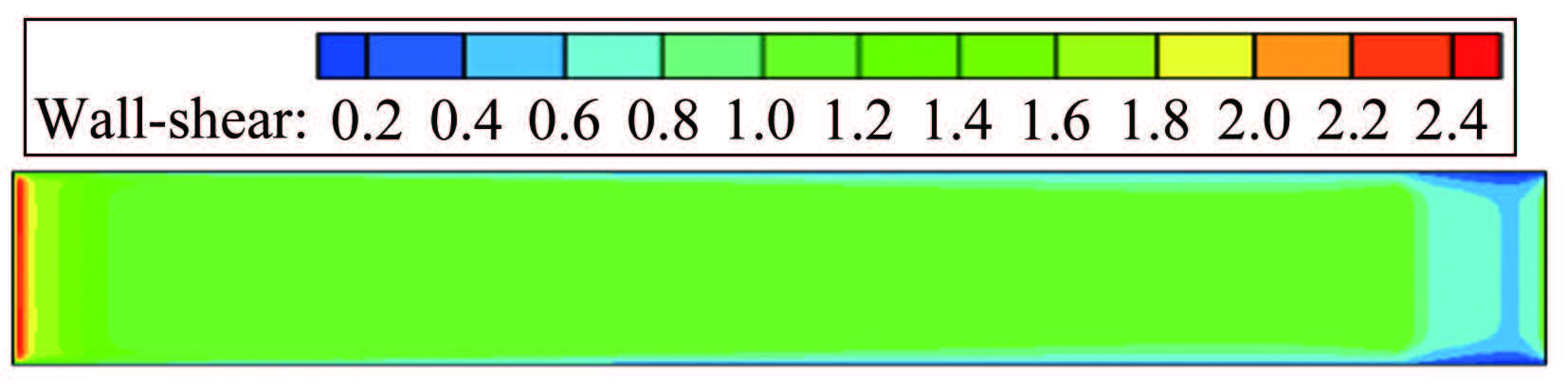
|
| 图 11 v=0.7m/s平板壁面剪应力云图 Fig.11 Contours of wall shear stress distribution(v=0.7m/s) |
表 3为不同外流速度下,测点处(距平板前缘800mm处)壁面剪应力数值计算与经验公式和速度剖面结果比较。可以看出不同流速下测点处数值计算结果与经验公式和速度剖面结果符合都较好。
外流速度 /(m·s-1) | CFD τw/Pa | 经验公式 τw/Pa | LDV速度剖面 τw/Pa |
| 0.5 | 0.5546 | 0.5463 | 0.5419 |
| 0.6 | 0.7745 | 0.7610 | 0.7632 |
| 0.7 | 1.0224 | 1.0058 | 1.0313 |
本文采用LDV技术测量平板边界层速度剖面的方法,在一小型精密水槽中获取零压力梯度光滑平板边界层的流动参数,并与数值仿真和经验公式计算结果分析比较,研究结果表明:
(1) 激光多普勒测速(LDV)技术能高精度地测量平板近壁面边界层的速度剖面,利用测得的速度数据进行从壁面到对数律层尾区全壁面律的拟合求解,获得壁面摩擦速度和其他边界层流动参数。速度剖面测得值与数值计算和经验公式计算结果符合较好,表明LDV测量结果可为水中MEMS壁面剪应力传感器标定提供理想的输入。
(2) 采用RANS方法、结合RNG k-ε湍流模型能较好地对水下平板绕流问题进行数值仿真,数值模拟结果与经验公式和速度剖面计算结果吻合较好,可以实现对平板边界层流动参数的预先估计。
| [1] | 樊星, 姜楠. 用平均速度剖面法测量壁面湍流摩擦阻力[J]. 力学与实践, 2005, 27(1): 28–30. Fan X, Jiang N. Skin friction measurement in turbulent boundary layer by mean velocity profile method[J]. Mechanics in Engineering, 2005, 27(1): 28–30. |
| [2] | Patel V C. Calibration of Preston tube and limitations on its use in pressure gradients[J]. Fluid Mechanics, 1965, 23: 185–208. DOI:10.1017/S0022112065001301 |
| [3] | 沈熊. 激光多普勒测速技术及应用[M]. 北京: 清华大学出版社, 2004. Shen X. Laser Doppler velocimetry and application[M]. Beijing: Tsinghua University Press, 2004. |
| [4] | Meinhart C D, Adrian R J. Measurement of the zero-pressure gradient turbulent boundary layer using particle image velocimetry[R]. AIAA-95-0789, 1995. |
| [5] | 王洪平, 高琪, 魏润杰, 等. 基于层析PIV的湍流边界层展向涡研究[J]. 实验流体力学, 2016, 30(2): 59–66. Wang H P, Gao Q, Wei R J, et al. Study of spanwise vortices in turbulent boundary layer flow based on tomographic PIV[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 59–66. |
| [6] | 王光华, 刘宝杰, 刘涛, 等. 利用PIV技术对平板湍流边界层的实验研究[J]. 自然科学进展, 1999, 9(12): 1198–1203. Wang G H, Liu B J, Liu T, et al. Experimental study of the turbulent boundary layer using PIV[J]. Progress in Natural Science, 1999, 9(12): 1198–1203. |
| [7] | 王晋军, 兰世隆, 苗福友. 沟槽面湍流边界层减阻特性研究[J]. 中国造船, 2001, 42(4): 1–5. Wang J J, Lan S L, Miao F Y. Drag-reduction characteristics of turbulent boundary layer flow over riblets surface[J]. Shipbuilding of China, 2001, 42(4): 1–5. |
| [8] | Niederschulte M A, Adrian R J, Hanratty T J. Measurements of turbulent flow in a channel at low Reynolds numbers[J]. Experiments in Fluids, 1990, 9: 222–230. |
| [9] | 李存标, 吴介之. 壁流动中的转捩[J]. 力学进展, 2009, 39(4): 480–507. Lee C B, Wu J Z. Transition in wall bounded flows[J]. Advance in Mechanics, 2009, 39(4): 480–507. |
| [10] | 何霖. 超声速边界层及激波与边界层相互作用的实验研究[D]. 长沙: 国防科技大学, 2011. He L. Experimental investigation of supersonic boundary layer and shock wave/boundary layer interaction[D]. Changsha: National University of Defense Technology, 2011. |
| [11] | Clauser F H. The turbulent boundary layer[J]. Advances in Applied Mechanics, 1956, 4: 1–51. DOI:10.1016/S0065-2156(08)70370-3 |
| [12] | Eggels J G M, Unger F, Weiss M H, et al. Fully developed turbulent pipe flow: A comparison between direct numerical simulation and experiment[J]. Fluid Mechanics, 1994, 268: 175–209. DOI:10.1017/S002211209400131X |
| [13] | Palikaras A, Yakinthos K, Goulas A. Transition on a flat plate with a semi-circular leading edge under uniform and positive shear free-stream flow[J]. International Journal of Heat and Fluid Flow, 2002, 23: 455–470. DOI:10.1016/S0142-727X(02)00146-7 |
| [14] | 崔杰. 湍流边界层速度分布的显式表示[J]. 空气动力学学报, 1994, 12(2): 208–211. Cui J. Explicit expression for the velocity distribution in a turbulent boundary layer[J]. Acta Aerodynamic Sinica, 1994, 12(2): 208–211. |
| [15] | 潘光, 黄桥高, 胡海豹, 等. 基于热线技术的脊状表面湍流边界层流动参数测试方法研究[J]. 测控技术, 2009, 28(4): 18–24. Pan G, Huang Q G, Hu H B. Research about the testing method of flow parameters of turbulent boundary layer over riblet surface based on hot wire technology[J]. Measurement&Control Technology, 2009, 28(4): 18–24. |
| [16] | Meloy J, Griffiny J, Sells J, et al. Experimental verification of a MEMS based skin friction sensor for quantitative wall shear stress measurement[C]. 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, Hawaii, 2011. |
| [17] | 王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. Wang F J. Computational fluid dynamics analysis -CFD software principles and applications[M]. Beijing: Tsinghua University Press, 2004. |
| [18] | 黄欢, 孙海浪, 田于逵, 等. 水下MEMS壁面剪应力传感器标定方案仿真分析与实验验证[J]. 实验流体力学, 2016, 30(2): 79–83,102. Huang H, Sun H M, Tian Y K, et al. CFD analysis and experimental validation on the scheme of calibration for Journal of Experiments in Fluid Mechanics[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 79–83,102. |



