在液体燃料冲压发动机的工作过程中,燃料的雾化质量直接影响后续的掺混和燃烧组织,进而影响发动机的工作性能[1]。冲压发动机中燃料的雾化过程包括一次雾化和二次雾化。二次雾化后的结果决定了最终的雾化质量。因此,对二次雾化机理的研究十分必要。
在气动力的作用下,单颗液滴变形破碎的过程称为二次雾化[2]。在不同的We 下,液滴的破碎形态也各不相同,HsiangL.P.[3]等根据前人的实验总结了牛顿流体We与破碎模式的关系。在高We下,液滴的破碎表现为灾型破碎模式[4]。一般认为, Rayleigh-Taylor(R-T)不稳定波的发展是液滴灾型 破碎的原因[5]。国内外学者对此进行了大量的实验与理论研究。Liu[6]最早提出液滴灾型破碎中出现的表面波是R-T不稳定波。Hwang[7]进行了柴油液滴在气流中破碎的实验,结果显示导致液滴灾型破碎的长波是R-T不稳定波。Joseph[8-9]采用激波管,研究了牛顿流体和粘弹性流体液滴在马赫数2~3时的破碎过程,分析比较了不同材料性质对液滴破碎的影响并进行了R-T不稳定性分析。Theofanous[10]进行了亚声速和超声速下液滴的破碎实验研究,发现在低We下也存在着R-T不稳定波的发展。蒋德军[11]以甘油水溶液模拟渣油沥青,实验研究了不同We下液滴的破碎,发现当We大于361时,液滴破碎为灾型破碎模式。赵辉[12]采用射流法研究了不同速度下水滴的破碎,进行了R-T不稳定性分析,认为可以将临界波数作为新的液滴破碎模式划分的依据。以上研究对液滴灾型破碎模式的描述大都局限在形态上,对R-T不稳定波的分析大都没有考虑液滴粘性和表面张力的影响,对影响R-T不稳定波发展因素的研究也不够充分与深入,有待做进一步的工作。
本文以煤油为工质,实验研究高韦伯数下液滴的破碎过程、不同气流速度下液滴的破碎形态和破碎时间,并根据R-T不稳定性理论,考虑液滴粘性和表面张力的影响,研究R-T不稳定波在液滴破碎过程中的作用,分析不同因素对R-T不稳定波发展的影响,并同实验结果进行对比。
1 实验系统与理论 1.1 实验装置与方法本文采用射流法[13]产生高速气流,实验系统如图 1所示。高压气罐中存储的压缩空气由喷口喷出后,形成高速气流。液滴发生器产生的煤油液滴进入主流区域后完成破碎过程,高速摄像机记录液滴破碎过程。

|
| 图 1 实验装置简图 Fig.1 Schematic of experimental devices |
高速摄像机型号为SpeedSense 9072,拍摄频率为14 438Hz。
实验中环境温度为275K,压强为0.1MPa,实验工况下煤油与空气的物性参数如表 1所示。
| Material | ρ/(kg·m-3) | μ/(Pa·s) | σ/(N·m-1) |
| Kerosene | 780 | 0.0024 | 0.00263 |
| Air | 1.29 | 0.00018 |
实验工况如表 2所示。
| Case | ug/(m·s-1) | T/K | d0/mm | We |
| 1 | 53 | 275 | 2.23 | 307 |
| 2 | 53 | 275 | 2.33 | 321 |
| 3 | 53 | 274 | 2.55 | 351 |
| 4 | 60 | 276 | 2.23 | 394 |
| 5 | 60 | 275 | 2.33 | 411 |
| 6 | 60 | 274 | 2.55 | 450 |
| 7 | 68 | 275 | 2.23 | 506 |
| 8 | 68 | 275 | 2.33 | 529 |
| 9 | 68 | 276 | 2.55 | 578 |
Rayleigh-Taylor不稳定性在液滴的破碎过程中起着重要的作用。当2种不同密度的流体之间存在相对加速度时,流体交界面便会产生不稳定的表面波,这就是R-T不稳定性。当液滴处在高速气流中时,由于气液两相间存在相对加速度,在液滴的迎风表面便会产生R-T不稳定波,如图 2所示。随着时间的推移,R-T不稳定波逐渐发展,其中具有最大增长率的波发展最快,并最终导致液滴的破碎。

|
| 图 2 Rayleigh-Taylor不稳定性破碎机理 Fig.2 Rayleigh-Taylor instability breakup mechanism |
Taylor[14]最先提出R-T不稳定性理论,并给出了理论公式。Chandrasekhar[15]在Taylor研究的基础之上,增加了对粘性和表面张力2个因素的考虑,得到了更完整的R-T不稳定性方程。但该方程过于复杂,不便于计算,得不到解析解。本文采用自编程序对该方程进行求解。根据文献[15],方程如下:
 (1)
(1)
式中:n为增长率,k为波数,a为液滴的初始加速度。
液滴置于高速气流中,主要受气流的气动力作用做加速运动,液滴重力、气流压差阻力等因素的影响可以忽略。于是,液滴的初始加速度[16]可以表达成:
 (2)
(2)
R-T不稳定波波数和波长之间存在如下关系:
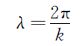 (3)
(3)
将R-T不稳定波的增长率趋于0时所对应的波长定义为临界波长。如果液滴的初始直径小于临界波长,认为液滴将不会发生破碎;如果液滴的初始直径大于临界波长,认为液滴将会发生破碎。
液滴破碎过程中R-T不稳定波的发展处于小扰动阶段,其发展过程符合指数规律:
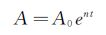 (4)
(4)
由于R-T不稳定波的发展速度决定了液滴的破碎时间,所以定义具有最大增长率的波的幅值增长为初始幅值的M倍所经历的时间,即
 (5)
(5)
在本文工况下,当We为321左右时,液滴开始呈现灾型破碎模式。从图中可以看出,在液滴进入高速气流中后,首先由球形迅速变为圆盘形,整个过程在不到1ms的时间内完成。这是因为在气动力的作用下,液滴的迎风面和背风面产生了一定的压差。高韦伯数下,该压力差很大,瞬间克服了粘性力和表面张力的作用,迫使液滴由球形变为圆盘形。
Hwang认为灾型破碎模式下的不稳定波是Kelvin-Helmholtz(K-H)和Rayleigh-Taylor 不稳定波。高速气流对液滴的剪切力使得液滴的外缘产生了K-H不稳定波,液滴对气流的相对加速度使得液滴的迎风面产生了R-T不稳定波。如图 3所示,在液滴变为圆盘形之后,由于K-H不稳定波的作用,在液滴的外缘不断有小液滴被剥离出来。另外,由于K-H不稳定波为短波,所以被剥离出来的小液滴的尺寸非常小。

|
| 图 3 煤油液滴的破碎过程 Fig.3 Stages in the breakup of a kerosene drop |
虽然液滴的表面有K-H不稳定波产生,但规模很小,它并不能使液滴在短时间内迅速破裂。真正导致液滴发生灾型破碎的不稳定波是R-T不稳定波。如图 3所示,由于气动力对液滴的加速作用,在液滴的迎风面产生了R-T不稳定波。随着时间的推移,R-T不稳定波逐渐发展,波动的幅度不断增大。最终,当R-T不稳定波的幅值超过临界值时,液滴便会在波谷处断裂,破碎成小液滴。由于R-T不稳定波是长波,所以液滴破碎后产生的小液滴尺寸较大。另外,根据图中的时间节点可以看出,波的发展速度非常快,所以液滴可以在短时间内完成破碎。
图 3(a)、(b)和(c)这3种工况下的We分别为351、450和411。图 3(a)和(b)相比,液滴的初始直径相同,气流速度不同。图 3(b)和(c)相比,液滴的初始直径不同,气流速度相同。对比图 3(a)、(b)和(c),可以看出:不同工况下液滴破碎过程中的形态变化基本相同,主要区别在于R-T不稳定波的波长。液滴初始直径相同的情况下,气流速度越大,波长越短。气流速度相同的条件下,液滴初始直径越大,波长越长。这与Joseph和Theofanous的实验结论一致。
从图 3(a)和(b)可以看出,We越大,波长越短,但对比图 3(b)和(c)可以发现We越大,波长越长,结论矛盾。所以,单纯用We来描述R-T不稳定波的波长以及液滴破碎后的尺寸是不合适的。
2.2 Rayleigh-Taylor不稳定性理论分析 2.2.1 气流速度对R-T不稳定波的影响给定液滴的初始直径为2.55mm,在不同的气流速度条件下求解式(1),得到了液滴表面 R-T不稳定波的波数和增长率之间的关系,如图 4所示。从图中可以看出,不管气流速度有多大,随着波数k的增大,增长率n都呈现出先增大后减小的趋势。这说明,只有某一特定波长的波才具有最快的发展速度,并且波长越远离这个临界值,其发展速度越小。另外,根据临界波数的定义可知,k-n曲线与k轴的右交点所对应的波数即为临界波数。

|
| 图 4 不同气流速度下的k-n图(d0=2.55mm) Fig.4 n vs. k at different gas velocities(d0=2.55mm) |
从图 4还可以看出,当气流速度增大时,对应的k-n曲线向右上方偏移,临界波数增大,增长率的最大值增大,并且增长率对应的波数也增大。这说明,随着速度的提高,临界波长减小,具有最大增长率的波的波长也减小,并且波的发展速度加快。反映到液滴的破碎过程中,临界波长减小会导致液滴发生破碎的最小直径减小,波长减小会导致液滴破碎后产生的子液滴的平均粒径变小,波的发展速度加快会导致液滴的破碎时间减小。上述分析与实验结果是一致的。
所以,对于气流式雾化方式,增大气流速度是提高雾化质量的有效途径。
2.2.2 液滴初始直径对R-T不稳定波的影响给定气流速度为68m/s,求解式(1),得到了不同初始直径液滴表面 R-T不稳定波的波数和增长率之间的关系,如图 5所示。从图中可以看出,在相同的来流条件下,液滴的初始直径越大,k-n曲线越向左下方偏移,临界波数越小,具有最大增长率的波的波数越小,并且对应的最大增长率也越小。这说明在相同的来流条件下,初始直径越大的液滴越容易破碎,并且破碎后的液滴尺寸越大,破碎时间越长。所以,在冲压发动机中,一次雾化产生的较大液滴会在高速气流的作用下发生二次破碎,这有效保证了最终的雾化质量。但应注意液滴二次破碎时间与整体雾化时间的关系,以保证液滴在进行燃烧之前完成破碎。

|
| 图 5 不同液滴初始直径下的k-n图(ug =68m/s) Fig.5 n vs. k with different initial diameters (ug =68m/s) |
实际上,由(2)式可以看出,液滴的初始加速度主要受液滴的初始直径和气流速度控制。因此,气流速度和液滴初始直径都是通过改变液滴的初始加速度来影响R-T不稳定波的产生与发展的。
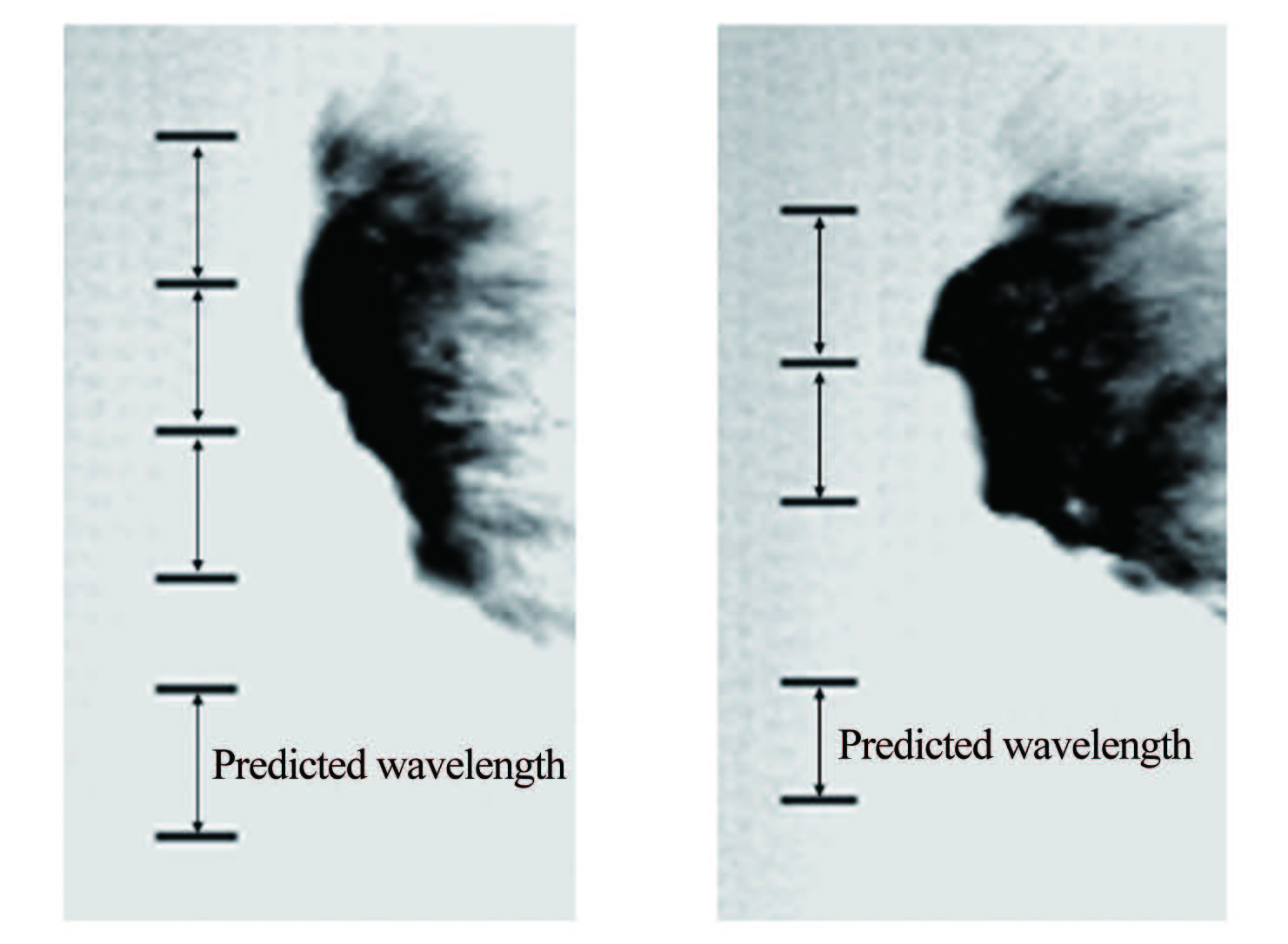
2.3 实验与理论计算对比 2.3.1 R-T不稳定波波长具有最大增长率的R-T不稳定波对液滴破碎起主导作用,在气液两相间形成波浪形的交界面,考虑到最大增长率的R-T不稳定波幅值最大,因此取液滴表面相邻且幅值最大的波峰(液滴表面的凸起)间的距离为波长。如图 6(a)和(b)所示,液滴左侧横线之间的距离为理论计算的波长,与液滴表面的波进行对比可以发现,理论计算的波长与实验结果接近。图 7给出了实验工况下液滴表面最大增长率R-T不稳定波波长的测量平均值与理论计算值的对比。从图中可以看出,实验结果与理论计算结果基本吻合,误差在5%以内。
|
| 图 6 Rayleigh-Taylor不稳定波的测量 Fig.6 Measurement of Rayleigh-Taylor waves |

|
| 图 7 理论波长与实验结果的对比 Fig.7 Comparison of wavelength between theory results and experimental data |
根据实验所得图片,将液滴完全停止破碎并且开始跟随气流同步运动的时刻定义为液滴破碎结束时刻,所经历的时间间隔即为液滴的破碎时间。理论计算取具有最大增长率的波的幅值增长为开始幅值的M倍所经历的时间为破碎时间。为了探究液滴破碎的机理,对真实破碎时间进行无量纲化[17]:
 (6)
(6)
式中:t为真实破碎时间。
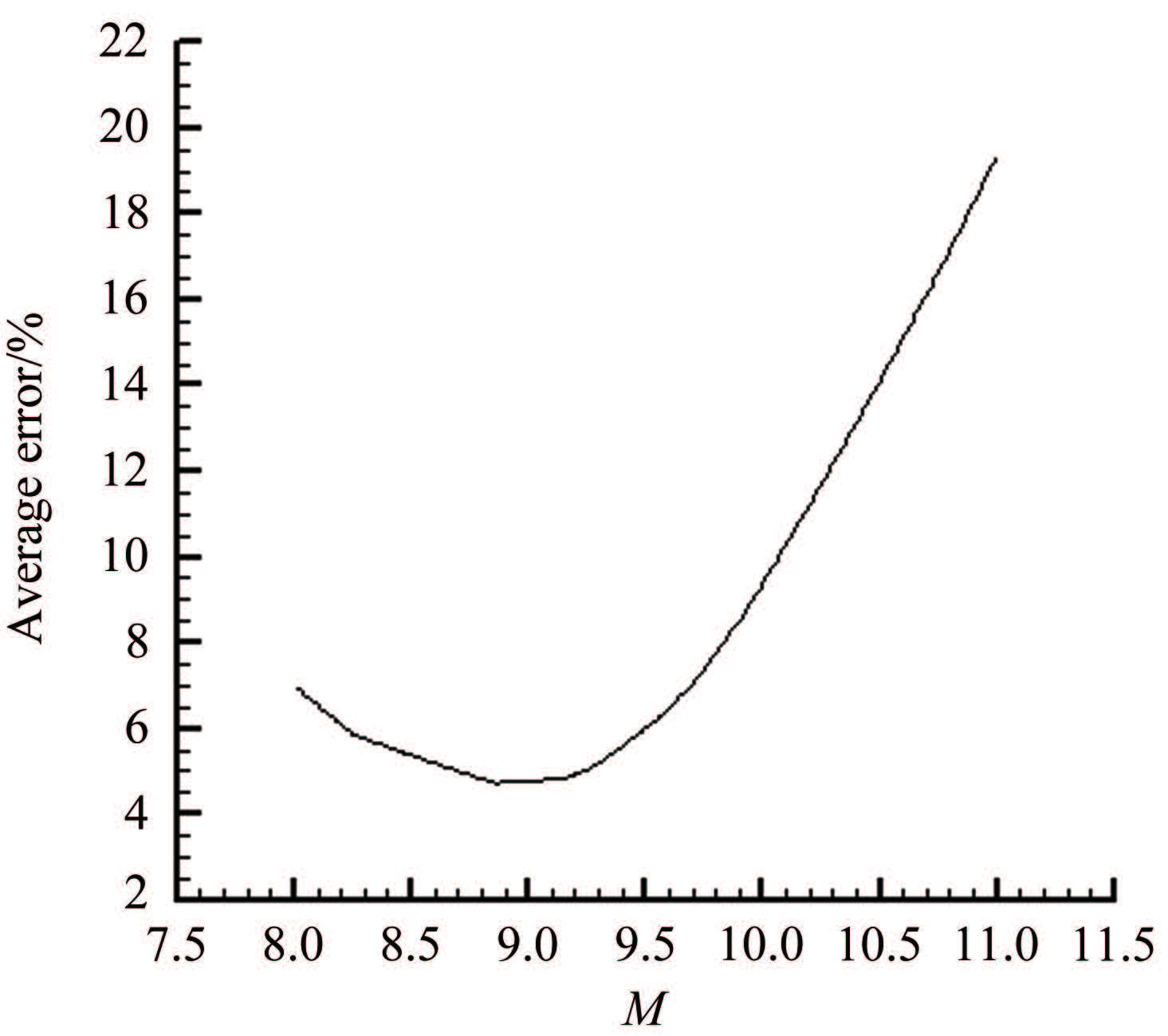
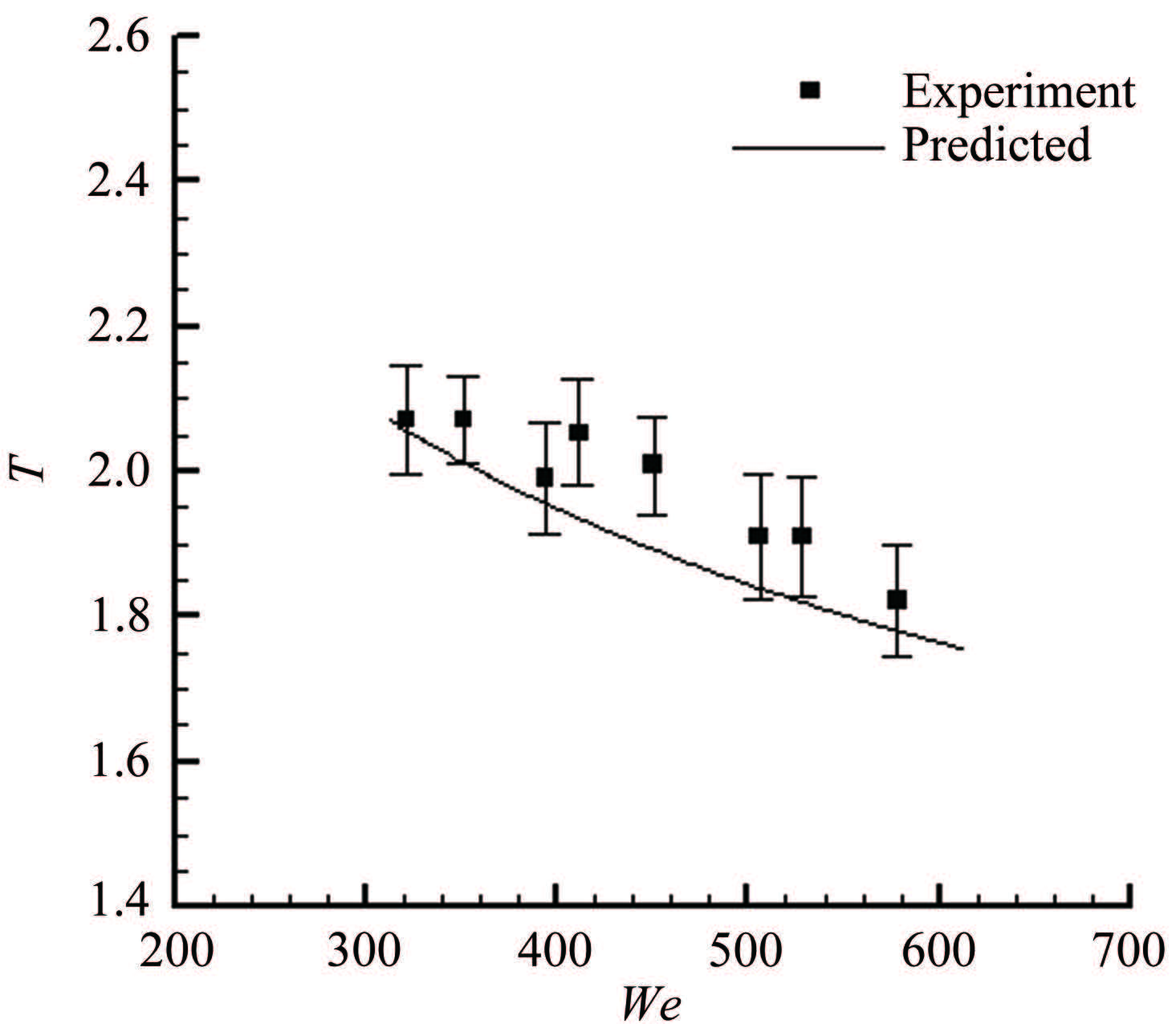
图 8为不同M值下理论计算结果和实验结果的平均误差。从图中可以看出,取经验参数为8.9左右时,计算结果和实验结果的平均误差最小,约为4.7%。当M=8.9时,不同We下的理论破碎时间和实验结果的对比如图 9所示。
|
| 图 8 M值与平均误差 Fig.8 Average error vs. M |
|
| 图 9 理论破碎时间与实验结果的对比 Fig.9 Comparison of breakup time between theory results and experimental data |
利用高速摄影对高韦伯数下煤油液滴的破碎过程进行了实验研究,利用R-T不稳定性理论分析计算了煤油液滴的破碎过程,可以得到以下结论:
(1) 当We为321左右时,煤油液滴开始呈现灾型破碎模式。
(2) 随着气流速度的增大,液滴初始直径减小,液滴表面具有最大增长率的R-T不稳定波的波长减小,增长率增大,临界波长减小。
(3) 考虑了粘性和表面张力的R-T不稳定性理论在预测最不稳定波长时,结论与实验结果的误差不超过5%。经验参数M取8.9时,R-T不稳定性理论预测煤油液滴的破碎时间最准确,平均误差不超过4.7%。
| [1] | 徐旭, 陈兵, 徐大军. 冲压发动机原理及技术[M]. 北京: 北京航空航天大学出版社, 2014: 193-195. Xu X, Chen B, Xu D J. Theory and technology of ramjet[M]. Beijing: Publishing House of Beihang University, 2014: 193-195. |
| [2] | 曹建明. 喷雾学[M]. 北京: 机械工业出版, 2005: 10-11. Cao J M. Atomization[M]. Beijing: Publishing House of Mechanical Industry, 2005: 10-11. |
| [3] | Hsiang L P, Faeth G M. Drop deformation and breakup due to shock wave and steady disturbances[J]. International Journal of Multiphase Flow, 1995, 21(4): 545–560. DOI:10.1016/0301-9322(94)00095-2 |
| [4] | 刘静. 超声速气流中横向燃油喷雾的数值模拟和实验研究[D]. 北京: 北京航空航天大学, 2010. Liu J. Numerical and experimental investigation of fuel spray in supersonic cross flow[D]. Beijing: Beihang University, 2010. |
| [5] | Guildenbecher D R, López-Rivera C, Sojka P E. Secondary atomization[J]. Experiments in Fluids, 2009, 46(3): 371–402. DOI:10.1007/s00348-008-0593-2 |
| [6] | Liu A B, Reitz R D. Mechanisms of air-assisted liquid atomization[J]. Atomization&Sprays, 1993, 3(1): 55–75. |
| [7] | Hwang S S, Liu Z, Reitz R D, et al. Breakup mechanisms and drag coefficients of high-speed vaporizing liquid drops[J]. Atomization&Sprays, 1996, 6(3): 353–376. |
| [8] | Joseph D D, Beavers G S, Funada T. Rayleigh-Taylor instability of viscoelastic drops at high Weber numbers[J]. Journal of Fluid Mechanics, 1999, 453(6): 109–132. |
| [9] | Joseph D D, Belanger J, Beavers G S. Breakup of a liquid drop suddenly exposed to a high-speed airstream[J]. International Journal of Multiphase Flow, 1999, 25(6-7): 1263–1303. DOI:10.1016/S0301-9322(99)00043-9 |
| [10] | Theofanous T G, Li G J, Dinh T N. Aerobreakup in rarefied supersonic gas flows[J]. Journal of Fluids Engineering, 2004, 126(4): 516–527. DOI:10.1115/1.1777234 |
| [11] | 蒋德军, 赵辉, 刘海峰, 等. 黏性流体的二次雾化特性[J]. 石油学报: 石油加工, 2011, 27(4): 572–582. Jiang D J, Zhao H, Liu H F, et al. Experimental characteristics of viscous fluid secondary breakup[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2011, 27(4): 572–582. |
| [12] | 赵辉. 同轴气流式雾化机理研究[D]. 上海: 华东理工大学, 2012. Zhao H. Studying on the mechanism of coaxial air-blast atomization[D]. Shanghai: East China University of Science and Technology, 2012. |
| [13] | Shraiber A A, Podvysotsky A M, Dubrovsky V V. Deformation and breakup of drops by aerodynamic forces[J]. Atomization&Sprays, 1996, 6(6): 667–692. |
| [14] | Taylor G I. The shape and acceleration of a drop in a high speed air stream[J]. The Scientific Papers of GI Taylor, 1963, 3: 457–464. |
| [15] | Chandrasekhar S. Hydrodynamic and hydromagnetic stability[D]. London: Oxford University Press, 1961. |
| [16] | Orourke P J, Amsden A A. The TAB method for numerical calculation of spray droplet breakup[C]. International Fuels and Lubricants Meeting and Exposition, Toronto, Ontario, 1987: 1. |
| [17] | Lopez R C. Secondary breakup of inelastic non-Newtonian liquid drops[D]. Indiana: Purdue University, 2010. |



