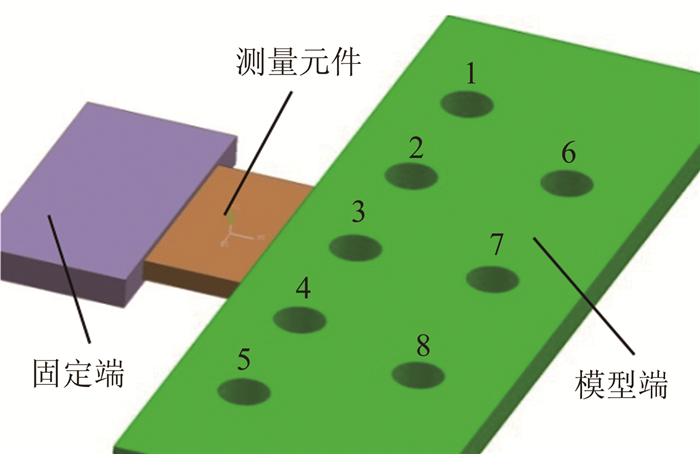
片式应变天平是一种常见的风洞试验测量设备,主要用来测量作用在飞行器操纵面(副翼、方向舵和升降舵)模型上的铰链力矩或作用在飞行器部件(机翼、翼尖小翼等)模型上的力和力矩[1-9]。受模型结构限制,片式应变天平外形通常为薄板状,天平测量元件截面的宽高比非常大(普遍超过10 :1),图 1所示为一传统整体式片式天平示意图,由固定端、模型端和测量元件组成,测量元件为整体薄板结构。其中将天平模型端面积做了适当放大,并布置了8个小孔,用于在不同位置施加载荷模拟不同连接状态。在实际应用中,传统片式天平测量主要存在2个问题:一是天平元件在不同连接状态下受载变形不一致,且天平实际应用状态又与校准状态不一致,造成天平测量的精准度不高;二是装配连接的影响,天平安装连接位置距离测量元件较近,装配预紧力在天平工作过程中难以保持稳定,同样会降低天平测量的精准度。
|
| 图 1 传统片式天平示意 Fig.1 Conventional thin slab strain gauge balance |
对于天平的装配连接,哈尔滨工业大学通过对铰矩天平进行各项加载试验和静态校准,分析对比静态校准结果和有限元分析计算结果,认为铰矩天平固定端合理的几何尺寸和较为合理的预紧力矩,可以减少铰矩天平的固定对测量元系数的影响,提高铰链力矩天平测量准确度[10];西北工业大学翼型、叶栅空气动力学国防科技重点实验室也对风洞天平的装配应力对元件输出值的干扰进行了研究并给出了一些设计建议[11]。受结构空间限制,片式天平在装配连接方面难以获得明显的改进。
要进一步提高片式天平的测量精准度,需要从天平元件在不同连接状态下受载变形不一致这个方面进行研究。印度科学理工学院通过改变天平元件结构,在三角翼上分别实现了三分量和六分量天平的设计[12]。中国航空工业空气动力研究院根据常规柱状轴向力元件设计思想,并结合有限元计算分析技术提出了一种在常规三分量片式铰链力矩天平基础上增加轴向力测量元件的方案,得到成功应用[13]。中国科学技术大学和中国空气动力研究与发展中心对片式天平元件进行了优化,提出了一种新型四分量片式铰链力矩天平,结构更加紧凑,测量效果良好[14]。中国空气动力研究与发展中心对因模型受载变形造成天平接口变形,从而引发的天平附加干扰信号影响天平准度的问题进行了研究并提出了解决措施[15]。上述片式天平中精准度较高的刚度较小,难以在一些部件测力(机翼、外翼等)上应用,刚度较好的精准度又不够高,不能得到很好的兼顾。
针对传统片式天平存在的主要问题,本文提出一种基于柱梁的片式天平研制技术,通过将传统片式天平整体式测量元件分解为多个柱梁的方式,在不明显降低天平整体刚度的基础上,提高测量的精准度,并进行有限元仿真分析和实验验证。
1 传统片式天平存在的主要问题传统片式天平采用矩形截面梁计算公式进行设计。在法向力Fy的作用下,矩形截面梁的最大应变εmax为:
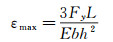 (1)
(1)
在弯矩M的作用下,矩形截面梁的最大应变εmax为:
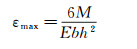 (2)
(2)
式中:Fy为天平法向力,M为天平弯矩,E为材料弹性模量,L为天平测量梁长度,b为天平测量梁截面宽度,h为测量梁截面高。
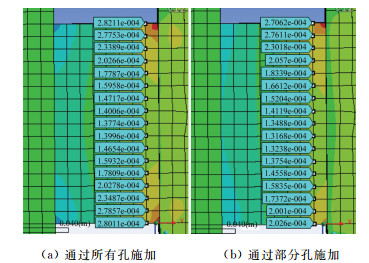
公式(1)和(2)成立的条件是测量元件的变形协调一致。传统的片式天平将应变计粘贴在关于天平元件中心对称的任意位置并组成惠斯通电桥进行测量。实际上,由于片式天平固定端和模型端尺寸受结构限制,厚度与测量元件接近,刚度相对天平元件不足,造成了天平元件在固定端或模型端不同连接状态下受载变形不一致,已经背离了矩形截面梁计算公式的前提假设。图 2所示为通过天平模型端所有孔加载和通过部分孔加载以模拟不同加载位置,施加同一载荷情况下测量元件同一截面的应变对比,可以看出,两者存在明显的差异,且平均应变也不一致,意味着在任何位置粘贴应变计均难以准确测量天平受到的实际载荷。
|
| 图 2 通过不同位置施加同一法向力时传统片式天平的应变差异 Fig.2 Strain difference of a conventional thin slab balance under the same normal force acting on different positions |
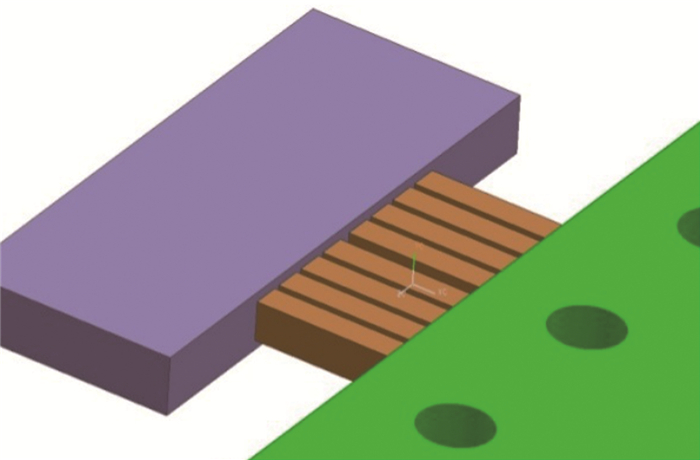
片式天平的整体结构决定了在不同连接状态下,其片式梁必然存在着变形不一致的情况。针对这种现象,提出一种采用柱梁组合代替片梁的方案:将片梁分割为多个柱梁的组合,如图 3所示。虽然多个柱梁组合而成的测量梁依旧不能解决在不同连接状态下总体变形不一致的情况,但对于单个柱梁,由于截面尺寸相对较小,单个柱梁的变形是协调一致的,适合公式(1)和(2)的前提假设,目前所有的单柱梁杆式天平的精准度均较高也表明其具有可行性。
|
| 图 3 由柱梁组成的片式天平示意 Fig.3 Thin slab balance based on beams |
如果将每个柱梁均看作1台独立的杆式天平元件,可以准确测量该柱梁承受的载荷,那么所有柱梁承受的载荷总和就可以被获知,从而得到该片式天平受到的载荷。在工程上,需要考虑连接结构和安装空间,不可能将片式天平的连接端对应每一根柱梁进行分割,因此,需要分析连接端为整体情况下的测量梁分割方案是否可行。
测量梁分割后,天平所受的载荷由n个柱梁共同承担,将每个柱梁均看做1台独立的杆式天平元件,由于连接端的刚度以及所处位置等因素,每个柱梁承受的载荷不同,但总载荷不变,即
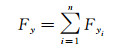 (3)
(3)
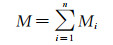 (4)
(4)
式中:Fy为天平法向力,Fyi为第i个柱梁承受的法向力,M为天平弯矩,Mi为第i个柱梁承受的弯矩。
在法向力Fy的作用下,第i个柱梁的最大应变εimax为:
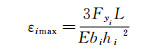 (5)
(5)
激励电压为U时该柱梁的输出信号为:
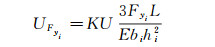 (6)
(6)
式中:K为应变计灵敏度系数,bi为第i个柱梁截面宽,hi为第i个柱梁截面高。
由于不知道每个柱梁承受的具体载荷,无法获得该柱梁的输出信号。但是如果将所有柱梁的截面尺寸取为一致,即:bi=b1,hi=h1,则可以得到激励电压为U时所有柱梁的平均输出信号:
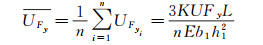 (7)
(7)
同理,在弯矩M作用下,激励电压为U时所有柱梁的平均输出信号为:
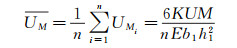 (8)
(8)
公式(7)和(8)成立的条件是所有柱梁的截面尺寸一致。从公式(7)和(8)可以看出,在激励电压一致的情况下,天平的最终平均输出信号只与施加的总载荷和单个柱梁的尺寸有关,不需要知道每个柱梁承受的具体载荷和信号输出,所以也不必将天平连接端对应每个柱梁进行分割。从公式(7)和(8)还可以看出,每个柱梁分别组成测量电桥后的平均输出和所有柱梁组成一个测量电桥的效果是一致的,实际应用中可以根据具体情况设计测量电桥。
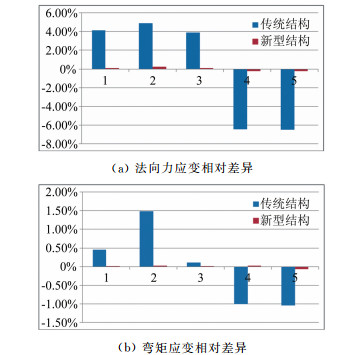
2.2 仿真分析通过有限元软件对传统片式天平和基于柱梁的新型片式天平进行了仿真分析。对上述传统和新型片式天平通过不同位置分别施加相同载荷,提取测量元件同一截面上的平均应变作为各自的测量应变,其中,法向力采用远程力(Remote force)的方式施加,力的作用中心为天平测量元件的对称中心。载荷施加位置共有5种不同方式(见表 1),图 4为通过不同位置施加相同弯矩载荷的示意图。在该5种方式下,分别获取了传统结构和新型结构片式天平的法向力和弯矩的各五组测量应变(见表 2和3),其中为了获得较大的应变值以方便统计分析,施加了较大的载荷。传统结构和新型结构片式天平法向力和弯矩测量应变与各自平均应变的相对差异对比如图 5所示。

|
| 图 4 5种施力方式 Fig.4 Five loading ways |
|
| 图 5 2种结构应变差异对比 Fig.5 Contrast of strain between conventional structure balance and new structure balance |
| 加载位置 | 一 | 二 | 三 | 四 | 五 |
| 对应孔 的编号 | 1, 2, 3, 4, 5, 6, 7, 8 | 1, 3, 5, 6, 8 | 1, 2, 3, 6, 7 | 3, 4, 5, 7, 8 | 2, 4, 7 |
| 加载位置 | 一 | 二 | 三 | 四 | 五 | |
| 测量应变 (×10-6) | 传统结构 | 1991.71 | 2006.82 | 1987.65 | 1789.53 | 1788.71 |
| 新结构 | 2420.46 | 2424.04 | 2420.13 | 2412.46 | 2412.54 | |
| 加载位置 | 一 | 二 | 三 | 四 | 五 | |
| 测量应变 (×10-6) | 传统结构 | 9001.12 | 9021 | 8994.71 | 8973.35 | 8972.65 |
| 新结构 | 9375.53 | 9375.87 | 9375.53 | 9375.80 | 9373.67 | |
从对比结果可以看出,传统的整体片式结构天平在不同位置施加相同载荷时的应变差异明显大于新型的柱梁组合元件结构的片式天平,新型结构的片式天平对于载荷施加的位置不敏感,更加适合于片式天平的测量工况。
2.3 验证及应用为了验证理论分析和仿真分析的结果,以2台精准度较差的现有片式天平为原型,分别是:某型号副翼天平、某型号升降舵天平(综合加载误差大于2%),在不改变其连接结构的前提下,设计了2台新型元件结构的片式天平,并分别采用原天平校准装置进行了静态校准,如图 6和7所示。校准结果如表 4和5所示。

|
| 图 6 新型副翼片式天平 Fig.6 New structure thin slab balance for aileron |

|
| 图 7 新型升降舵片式天平 Fig.7 New structure thin slab balance for elevator |
| 测量分量 | Y | Mx | Mj | |
| 设计载荷/(N、N·m) | 500 | 25 | 15 | |
| 主项 | +Y向/(N·mV-1) | 95.6147 | 5.5914 | 2.0143 |
| 系数 | -Y向/(N·mV-1) | 95.6373 | 5.5763 | 2.0146 |
| 差异 | 相对差异/% | 0.024 | 0.27 | 0.015 |
| 综合加载误差/(%FS) | 0.057 | 0.10 | 0.14 | |
| 法向力模拟加载相对误差/% | <0.3 | |||
| 测量分量 | Y | Mx | Mj | |
| 设计载荷/(N、N·m) | 910 | 30 | 25 | |
| 主项 | +Y向/(N·mV-1) | 69.0955 | 3.6151 | 1.1941 |
| 系数 | -Y向/(N·mV-1) | 69.0589 | 3.6143 | 1.1909 |
| 差异 | 相对差异/% | 0.053 | 0.022 | 0.27 |
| 综合加载误差/(%FS) | 0.015 | 0.3 | 0.09 | |
| 法向力模拟加载相对误差/% | <0.5 | |||
静态校准结果显示:2台天平各分量正负向的主项系数一致性好,校准结果良好,对天平进行加载检验,即去掉校准加载头后在天平模型端任意位置悬挂标准砝码,法向力的相对误差均小于0.5%,满足试验测量需要。
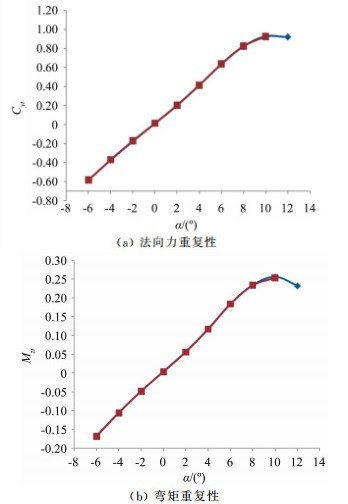
基于柱梁的新型片式天平研制技术目前在中国空气动力研究与发展中心高速所已成功应用于某飞机外翼部件测力和某飞机机翼部件测力等多个风洞测力试验项目。图 8所示为某飞机外翼部件测力试验Ma=1.05时的重复性曲线,在该项试验过程中,采用基于柱梁的新型片式天平性能稳定、测值准确,为型号研制提供了满意的试验数据。
|
| 图 8 某飞机外翼部件测力Ma=1.05重复性 Fig.8 Repeatability of outer wing force test for an aircraft (Ma=1.05) |
(1)采用有限元仿真分析软件在天平模型端不同位置施加同一载荷的方式,模拟天平不同的连接状态,可以作为预测片式天平测量可靠性的一个有效手段。
(2)相对于传统的片式天平,基于柱梁的片式天平对于连接状态的敏感性要小的多,测量精准度高,更适合于风洞测力试验。
| [1] | 贺德馨. 风洞天平[M]. 北京: 国防工业出版社 ,2001 . |
| [2] | 舒海峰, 徐晓斌, 孙鹏. 高超声速风洞多天平测力试验技术研究[J]. 实验流体力学 , 2014, 28 (4) : 49–53. Shu H F, Xu X B, Sun P. Technique investigation on force test with multi-balance in hypersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2014, 28 (4) : 49–53. |
| [3] | 黄宗波, 王勋年, 章荣平. 舵面铰链力矩及其缝隙效应研究[J]. 实验流体力学 , 2007, 21 (4) : 1–6. Huang Z B, Wang X N, Zhang R P. Investigation of gap effect on the rudder hinge moment characteristics[J]. Journal of Experiments in Fluid Mechanics , 2007, 21 (4) : 1–6. |
| [4] | 王明, 但聃, 陈丽. 飞机舱门类部件气动载荷风洞试验研究[J]. 实验流体力学 , 2012, 26 (4) : 18–21. Wang M, Dan D, Chen L. Research on aerodynamic load of aircraft door components in wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2012, 26 (4) : 18–21. |
| [5] | 熊琳, 刘展, 陈河梧. 舵面天平技术及其在高超声速风洞的应用研究[J]. 实验流体力学 , 2007, 21 (3) : 55–57. Xiong L, Liu Z, Chen H W. Hinge moment balance technique and application in hypersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2007, 21 (3) : 55–57. |
| [6] | 李方吉, 高超, 李为群, 等. 某复杂构型导弹高速风洞部件测力实验研究[J]. 实验流体力学 , 2014, 28 (5) : 65–70. Li F J, Gao C, Li W Q, et al. The component characteristics test study of a missile model with complexity configuration in high speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2014, 28 (5) : 65–70. |
| [7] | 顾岩, 虞伟建. 有限元分析法在风洞天平中的应用[J]. 流体力学实验与测量 , 1999 (4) : 82–86. Gu Y, Yu W J. The application of finite element analysis in wind-tunnel balance[J]. Experiments and Measurements in Fluid Mechanics , 1999 (4) : 82–86. |
| [8] | 刘高计, 谌满荣, 于卫青, 等. 风洞应变天平灵敏度设计方法研究[J]. 弹箭与制导学报 , 2006, 2 : 94–97. Liu G J, Chen M R, Yu W Q, et al. Design methods for wind tunnel strain gauge balance sensitivity[J]. Journal of Projectiles, Rockets, Missiles and Guidance , 2006, 2 : 94–97. |
| [9] | 王惠伦, 解亚军, 姜亚军, 等. 一种提高风洞天平灵敏度的测量方法[J]. 实验流体力学 , 2015, 29 (1) : 83–86. Wang H L, Xie Y J, Jiang Y J, et al. A new method for improving the measurement sensitivity of wind tunnel balance[J]. Journal of Experiments in Fluid Mechanics , 2015, 29 (1) : 83–86. |
| [10] | 张丹, 胡胜海, 王洪光. 铰矩天平固定方式及预紧力矩对其测量影响的研究[J]. 宇航计测技术 , 2013, 33 (6) : 46–49. Zhang D, Hu S H, Wang H G. Research on influence of fixed model and pretightening moment on the hinge moment balance measures[J]. Journal of Astronautic Metrology and Measurement , 2013, 33 (6) : 46–49. |
| [11] | 王惠伦, 解亚军. 风洞天平装配应力分析[J]. 航空工程进展 , 2014, 5 (3) : 364–368. Wang H L, Xie Y J. Analysis of assembly stress of wind tunnel balance[J]. Advances in Aeronautical Science and Engineering , 2014, 5 (3) : 364–368. |
| [12] | Ramesh R, Ramaswamy M A, Vasudevan B. Thin flat internal strain gauge balances for testing slab delta wing models at hypersonic speeds[J]. Instrumentation in Aerospace Simulation Facilities , 1995 . |
| [13] | 刘喜贺, 王天昊, 邱俊文, 等. 四分量片式铰链力矩天平技术及风洞实验应用研究[J]. 实验流体力学 , 2011, 25 (2) : 88–91. Liu X H, Wang T H, Qiu J W, et al. Hinge moment balance technique with axial force measurement and its application in wind tunnel test[J]. Journal of Experiments in Fluid Mechanics , 2011, 25 (2) : 88–91. |
| [14] | 潘华烨, 张青川, 王树民. 新型四分量片式铰链力矩天平研制与应用[J]. 弹箭与制导学报 , 2015, 35 (2) : 129–133. Pan H Y, Zhang Q C, Wang S M. Development and application of a novel four components plate type hinge moment balance[J]. Journal of Projectiles, Rockets, Missiles and Guidance , 2015, 35 (2) : 129–133. |
| [15] | 贾巍, 刘维亮. 某型无人机片式铰链力矩天平研制[J]. 气动研究与发展 , 2011, 21 (4) : 44–47. Jia W, Liu W L. Development of flaky hinge moment balances of an unmanned aerial vehicle[J]. Aerodynamics Research and Development , 2011, 21 (4) : 44–47. |



