随着飞行器机动性、敏捷性要求的不断提高,以及超声速/高超声速飞行器的不断出现,超声速颤振问题逐渐引起了飞行器设计部门的广泛重视。
目前颤振研究主要有理论计算、风洞试验和飞行试验3种手段[1],其中风洞试验是获取飞行器颤振边界最经济、最行之有效的手段。但国内的超声速风洞均为暂冲式风洞,风洞起动/关车时存在较大的冲击载荷(见图 1),对试验模型的强度、刚度要求较高[2],因此国内之前很少进行超声速颤振试验,理论分析依然是超声速、高超声速气动弹性设计和研究的主要途径[3]。
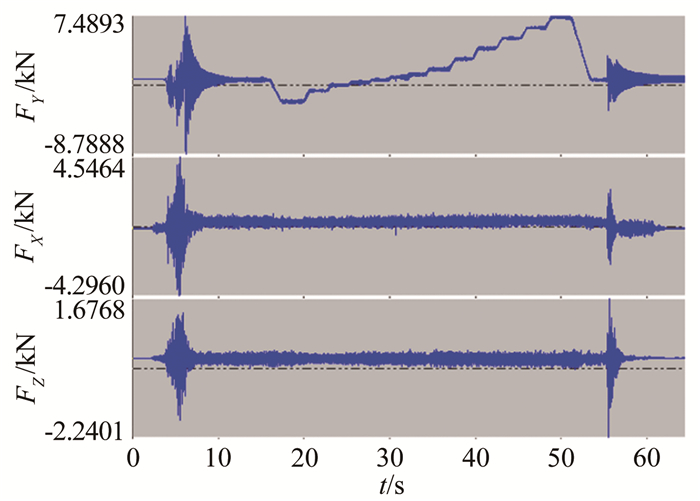
|
| 图 1 2m×2m超声速风洞冲击载荷示意 Fig.1 Impact load in 2m×2m supersonic wind tunnel |
现代飞行器结构布局形式、结构形态越来越复杂,而且新型复合材料得到广泛应用,飞行器大迎角运动、激波运动引起的气动力非线性、结构非线性、间隙非线性均增加了数值计算获取超声速颤振边界的难度。近年来,国内多个导弹型号在设计过程中遇到或出现了颤振问题,己定型批量生产的某型地空导弹,抽检飞行试验曾发生多次折断事故[4],这说明仅通过理论计算获得现代飞行器的颤振边界并不可靠。
鉴于飞行器设计部门对超声速颤振风洞试验日益迫切的需求,建立一套普适性较强、工程实用的超声速颤振风洞试验系统迫在眉睫。
美国于19世纪60年代建立了超声速颤振试验技术,并进行了一系列风洞试验[5]。NASA曾在Langley研究中心的9 in×18 in暂冲式超声速风洞采用侧壁支撑的方式进行了某全动鸭翼Ma=1.3、2.0、2.55的超声速颤振试验[6],该鸭翼具有足够的强度可承受风洞的起动/关车冲击;波音公司在Ames研究中心的1.8m连续式风洞进行了某超声速运输机样机机翼的超声速颤振试验[7];洛克希德·马丁公司在AEDC的4T连续式风洞进行了F22垂尾Ma=1.41的超声速颤振风洞试验,并获得了需要的颤振点[8]。上述2座风洞均为连续式风洞,不存在起动/关车的冲击载荷,因此模型均直接安装在风洞壁板上。国内在超声速颤振方面的研究主要集中在理论计算上,风洞试验开展较少。上海航天技术研究院第八设计部的杨炳渊等人在FD-06暂冲式超声速风洞进行了某型号导弹舵面模型Ma=1.5~3.0的超声速颤振风洞试验[9];中国航天空气动力技术研究院的季辰等人在FD-07高超声速风洞进行了Ma=5.0、6.0的颤振试验技术研究[10],并设计了专门的可伸缩保护罩来避免风洞起动/关车的冲击载荷。
依托国内现有的暂冲式风洞建立超声速颤振试验技术首先要解决冲击载荷对试验模型的影响,要么模型具有足够的强度,要么风洞起动/关车时对模型有一定的保护措施。显然足够的强度对大部分动力学相似的颤振模型来说是不现实的,尤其部分模型还安装有实物舵机,在超声速风洞起动/关车载荷的冲击下很容易损坏。给模型加装保护罩可以解决这个问题,但是对于较大的模型加装保护罩可能导致模型堵塞度太大,流场无法建立,并且针对不同的模型可能要设计专门的保护罩,普适性不强。为解决这个问题,在FL-23风洞研制一套普适性较好、工程实用的超声速颤振试验投放系统。
1 超声速颤振试验投放系统建立超声速颤振试验技术主要包含变速压流场控制、模型防护和数据处理3个方面,之前已经具备了成熟的流场控制技术及数据处理软件[11-12],因此在FL-23风洞建立超声速颤振试验技术的主要难点在模型防护方面。通过对风洞条件的分析,项目组准备采用模型投放的方式来实现对模型的防护。
根据超声速颤振试验的需求,该投放系统主要应具备以下特点:
(1)投放系统应保护模型不受风洞起动/关车时流场的冲击;
(2)投放系统应具有足够快的响应速度,在模型发生颤振时能快速实现防护;
(3)投放系统应具有足够高的支撑频率,避免干扰试验模型的动力学特性;
(4)投放系统安装/投放到位时应不影响风洞的流场品质;
(5)投放系统应具有足够的运动行程,以适应多种尺寸的模型。
为了实现上述目标,根据FL-23风洞的结构特点,在图 2所示的风洞侧壁驻室处研制了一套颤振试验投放系统。具体工作原理如下:风洞起动前模型位于投放机构驻室内,待冲击结束、流场稳定后,投放机构将模型送入流场并锁死,再采用阶梯/连续变速压方式进行颤振试验。当模型发生颤振或试验结束后,模型快速收回投放机构驻室,然后风洞降压关车,从而防止模型颤振或关车时损坏模型。

|
| 图 2 试验段侧壁驻室(颤振投放机构安装位置) Fig.2 Wind tunnel test section sidewall |
颤振投放系统主要由投放机构、驻室密封框、控制箱和空气压缩机4部分组成,具体如图 3所示。
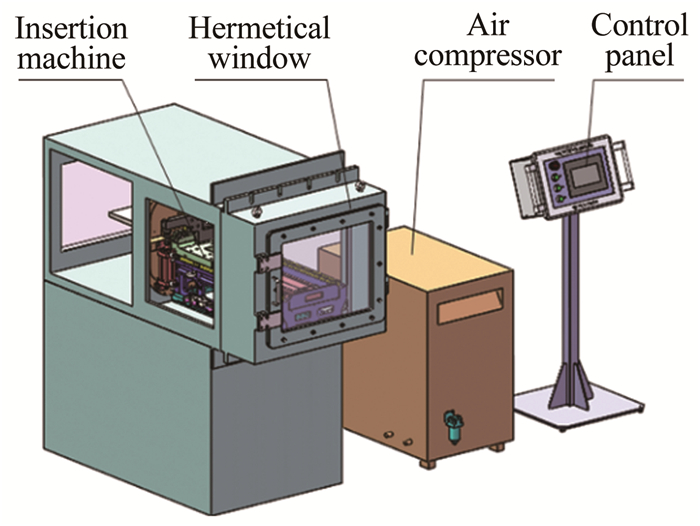
|
| 图 3 投放系统组成示意图 Fig.3 Sketch of the insertion system |
投放机构是颤振投放系统的执行单元,完成试验模型的快速投放和回收功能,实现上文第(1)、(2)点需求;为保证投放机构的行程,对驻室进行了延长,驻室密封框完成了加长部分的密封,实现上文第(4)、(5)点需求;控制箱完成系统的控制和人机交互;空气压缩机为投放机构动作提供动力。
投放机构主要由侧壁钢窗、进给气缸、插板、锁紧气缸、锁紧斜块、电磁阀和安装基座等组成,具体如图 4所示。侧壁钢窗与风洞内侧壁平齐,留有模型的投放入口,实现上文第(4)点需求;进给气缸带动插板上的模型前后运动,实现试验模型的快速投放和回收;锁紧气缸带动锁紧斜块上下运动,实现进给插板的锁紧和放松,实现上文第(3)点对机构支撑频率的需求。
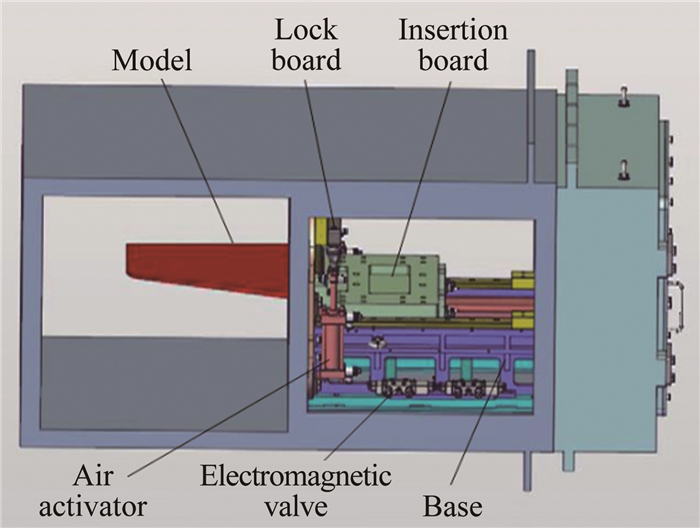
|
| 图 4 投放机构组成示意图 Fig.4 Sketch of the insertion machine |
研制成功的投放机构具有以下性能指标:机构运动范围为0~500mm,位置精度0.1mm,运动速度为0~300mm/s,支撑频率高于100Hz,能够实现超声速颤振试验的需求,并且适用于多种刚度、尺寸及外形的试验模型。
2 风洞及试验模型FL-23风洞是一座直流暂冲式亚、跨、超声速风洞,试验段尺寸为0.6m×0.6m×2.5m,试验Ma数0.4~4.5[13]。总压范围105~736kPa,总压控制精度0.2%~0.3%,对应的速压范围如图 5所示,可以看出超声速时FL-23风洞速压变化范围较宽,适合进行颤振试验。
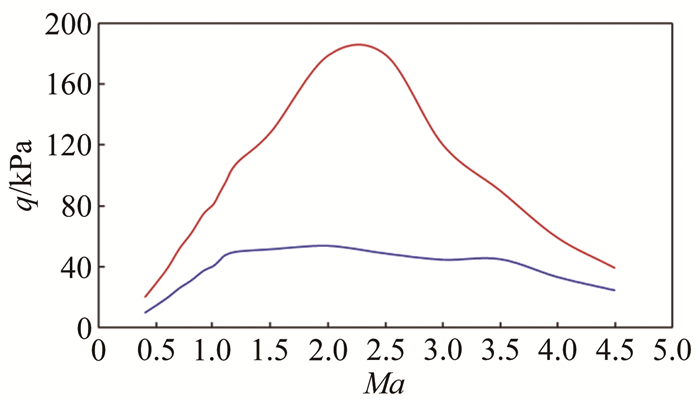
|
| 图 5 FL-23风洞速压范围 Fig.5 Dynamic pressure of FL-23 wind tunnel |
风洞试验模型为图 6所示的舵面模型,舵面厚6mm,展长360mm,根弦长400mm,材料为航空铝。模型安装在投放机构插板上,完全投入流场时在风洞中的阻塞度约为0.5%。

|
| 图 6 模型在风洞中的安装照片 Fig.6 Model in the wind tunnel |
风洞试验前对模型进行了地面振动试验,测得舵面的一阶弯曲频率为29.02Hz,一阶扭转频率为87.58Hz。风洞试验时,模型根部粘贴电阻丝应变片,用来测量模型的弯曲、扭转振动信号。应变电桥的信号线通过投放机构的走线孔引入驻室,再从后盖板引出并与测试仪器相连。
3 试验方法与数据处理 3.1 地面振动试验为了检查模型,在风洞安装状态用LMS模态试验系统对模型进行了地面振动试验。同时,为保证风洞试验前后模型及支撑装置状态正常,进行了校核性振动试验,即使用力锤对颤振模型施加激励,利用NI测试设备获得模型内应变的响应信号,通过功率谱分析获得模型的振动频率。
3.2 模型防护为了避免模型发生颤振损坏风洞,主要采用了计算机程控关车及人工监视关车[14]。计算机程控关车通过软件来实现,采集软件连续监测模型的振动信号,如果在预设的时间内有预设数目波形的峰值超过了参考电压,就由计算机发出指令,投放机构快速回收。人工监视关车主要依靠风洞侧壁驻室安装的摄像机远程监控试验情况,可人工发送指令快速回收投放机构。
3.3 风洞试验颤振试验采用定Ma数阶梯变总压的开车方式来实现阶梯变速压,并实时记录模型的振动信号。试验过程中,模型的振动信号通过SCXI-1520程控放大器调理放大后,由PXI-6280数据采集设备实时采集,然后传输到计算机,实时存储、显示所有通道信号的时间历程。
为了实时监测流场参数的变化,由专用采集设备获得风洞的总压、静压、总温,通过计算获得来流速压、密度等流场参数,供颤振特性分析时参考。另外,还同步采集风洞控制系统发来的阶梯信号和紧急关车信号。
3.4 数据处理超声速颤振试验与跨声速颤振试验在数据处理方法并无明显不同,主要分以下4步[15]:
(a)预处理。截取试验数据中的有效数据,去除趋势项,去除直流分量,并根据风洞试验中模型的振动频率范围进行数字滤波。
(b)随机衰减法。运用随机衰减法去除风洞气流噪声引起的随机干扰响应。
(c)模态参数辨识。选取矩阵束(Matrix Pencil,简称MP)方法进行模态参数辨识,获得模型的振动频率和阻尼比。
(d)颤振边界外插。采用阻尼比或功率谱峰值倒数外插获得颤振临界速压。
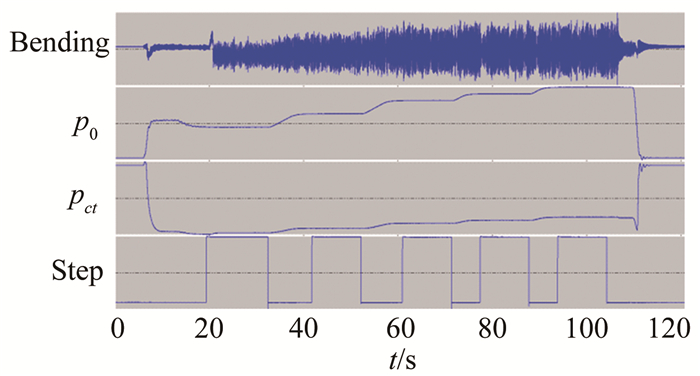
4 试验结果超声速颤振风洞试验的流程与跨声速颤振试验并无明显差别,主要区别在于超声速颤振风洞试验中,模型在流场稳定后才由投放机构送入流场。本次试验进行了Ma=1.5、2.0的超声速颤振试验,图 7给出了Ma=1.5时舵面模型的典型振动响应时间历程。
|
| 图 7 舵面模型振动响应信号(Ma=1.5) Fig.7 Vibration response signals of the rudder (Ma=1.5) |
可以看出:风洞启动前模型位于投放机构驻室内,基本不会受到流场的冲击,模型振动不明显。流场稳定后,投放机构将模型送入流场,模型振动显著加剧。风洞关车前,模型收入投放机构驻室,模型振动幅度明显减小。从时域信号可以看出,投放机构能够有效地保护模型不受起动/关车冲击的影响。试验过程中,总压控制平稳,没有出现超调现象,完全可以满足颤振试验的需求。
表 1给出了舵面模型颤振稳定性参数的测量结果,可以看出Ma=1.5的试验速压已接近风洞速压上边界,但颤振稳定性参数的规律性较差,无法外插出可靠的颤振边界。而Ma=2.0的试验速压距亚临界较远,同样无法外插出可靠的颤振边界。
| Ma | Step | q/kPa | 1/A | f/Hz | γ/% |
| 1 | 67.87 | 1.000 | 38.05 | 3.599 | |
| 2 | 78.73 | 1.267 | 39.50 | 3.927 | |
| 2.0 | 3 | 85.84 | 1.491 | 40.81 | 4.633 |
| 4 | 93.01 | 1.327 | 42.22 | 4.557 | |
| 5 | 100.18 | 0.868 | 42.92 | 3.964 | |
| 1 | 85.79 | 1.000 | 42.83 | 0.674 | |
| 2 | 96.47 | 1.276 | 43.32 | 0.977 | |
| 1.5 | 3 | 107.20 | 1.376 | 43.29 | 0.980 |
| 4 | 115.78 | 1.815 | 43.78 | 1.446 | |
| 5 | 120.00 | 2.842 | 43.96 | 1.930 |
由于本次试验的主要目的是检验颤振投放机构的性能指标,为节约经费,试验模型未进行专门的设计加工,导致模型的超声速颤振临界速压较高,未获得模型的超声速颤振临界点。不过在后续的型号风洞试验过程中,成功获得了某飞行器Ma=3.0、4.0的颤振点,并且亚临界外插的结果与风洞直吹颤振结果一致性非常好。由于型号设计部门后续可能发表相关文章,在此不详述试验结果。
不过经数值计算发现该模型的跨声速颤振边界在风洞速压范围内,为进一步检验数据处理方法,又进行了Ma=1.2、0.8的颤振试验,并获得了Ma=1.2、0.8的颤振点。
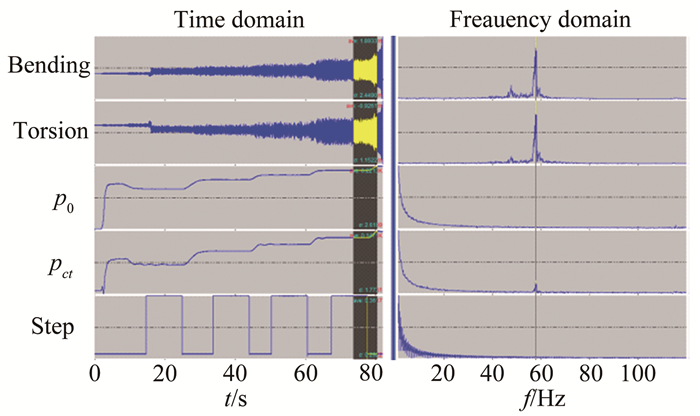
图 8给出了Ma=0.8时舵面模型的典型振动响应时间历程。可以看出,随着速压的增加,舵面模型发生了明显颤振现象,此时舵面的颤振速压约为64.35kPa,颤振频率约为58.3Hz,是典型的弯扭耦合颤振。
|
| 图 8 舵面模型振动响应信号(Ma=0.8) Fig.8 Vibration response signals of the rudder (Ma=0.8) |
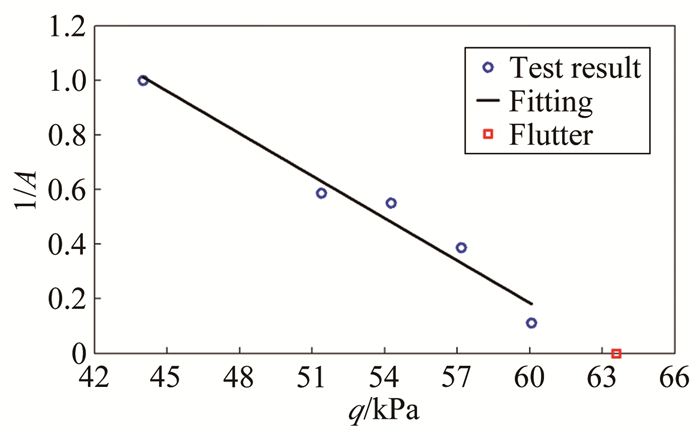
为了逐步逼近颤振边界,在Ma=0.8条件下进行了2个车次的风洞试验,表 2给出了低速压车次的颤振稳定性参数测量结果,图 9给出了Ma=0.8时颤振稳定性参数的插值结果。可以看出, 通过峰值导数外插出的颤振临界速压为63.58kPa,与试验获得的颤振速压64.35kPa基本一致,再次验证了本文采用的数据处理方法的可靠性。
| Ma | Step | q/kPa | 1/A | f/Hz | γ/% |
| 1 | 62.30 | 1.000 | 47.95 | 2.960 | |
| 1.2 | 2 | 68.50 | 0.640 | 48.26 | 1.774 |
| 3 | 74.71 | 0.192 | 48.44 | 1.183 | |
| 1 | 44.02 | 1.000 | 68.50 | 2.324 | |
| 2 | 51.39 | 0.586 | 67.14 | 4.718 | |
| 0.8 | 3 | 54.27 | 0.551 | 65.16 | 4.599 |
| 4 | 57.18 | 0.387 | 62.48 | 4.593 | |
| 5 | 60.08 | 0.111 | 59.75 | 2.391 |
|
| 图 9 亚临界预测结果(Ma=0.8) Fig.9 Subcritical prediction of flutter parameter(Ma=0.8) |
(1)所研制的超声速颤振试验投放系统能够有效防止风洞起动/关车冲击载荷损坏模型,放宽了超声速颤振试验模型强度的限制;
(2)超声速颤振试验投放系统能够适应多种尺寸、外形的试验模型;
(3)采用亚临界预测方法获得了试验模型跨声速范围的颤振临界速压及某飞行器超声速颤振临界速压,且与吹风结果一致;
(4)建立了工程实用的超声速颤振试验平台。
| [1] | 张伟伟, 钟华寿, 肖华, 等. 颤振飞行试验的边界预测方法回顾与展望[J]. 航空学报 , 2015, 36 (5) : 1367–1384. Zhang W W, Zhong H S, Xiao H, et al. Review and prospect of flutter boundary prediction methods for flight flutter testing[J]. Acta Aeronautica et Astronautica Sinica , 2015, 36 (5) : 1367–1384. |
| [2] | 陈建中, 赵忠良, 涂正光, 等. 栅格舵气动与操纵特性高速风洞试验技术研究[J]. 实验流体力学 , 2011, 25 (6) : 82–87. Chen J Z, Zhao Z L, Tu Z G, et al. Test technique investigation for aerodynamics and controlling capability of a grid fin in high speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2011, 25 (6) : 82–87. |
| [3] | 史晓鸣.基于当地流活塞理论的全机组合体颤振及气动伺服弹性分析[D].上海:复旦大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10246-1012331250.htm |
| [4] | 樊则文.导弹伺服气动弹性稳定性分析方法研究[D].西安:西北工业大学, 2005. |
| [5] | Terry M H, Lawrence J H. Aeroelasticity research at wright-patterson air force base (wright field) from 1953-1993[J]. Journal of Aircraft , 2003, 40 (5) : 813–819. DOI:10.2514/2.6872 |
| [6] | Charles L R, Tuovila W J. Transonic and supersonic flutter investigation of 1/2-size models of all-movable canard surface of an expendable powered target[R]. NASA AD 3164, 1961. |
| [7] | William D A. The aeroelastic design and testing of the F/A-22[C]. 2005 USAF Aircraft Structural Integrity Program Conference, Memphis, Tennessee, USA, 2005. |
| [8] | William D A. The aeroelastic design and testing of the F/A-22[C]. 2005 USAF Aircraft Structural Integrity Program Conference, Memphis, Tennessee, USA, 2005. |
| [9] | 杨炳渊, 宋伟力. 应用当地流活塞理论的大攻角升力面颤振气动力表达式[J]. 上海力学 , 1999, 20 (3) : 223–228. |
| [10] | 季辰, 李锋, 刘子强. 高超声速风洞颤振试验技术研究[J]. 实验流体力学 , 2015, 29 (4) : 75–80. Ji C, Li F, Liu Z Q. Research on flutter test technique in hypersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2015, 29 (4) : 75–80. |
| [11] | 高鹏, 郭洪涛, 余立, 等. 0.6米风洞亚跨声速连续变速压运行方式研究[C]//中国空气动力测控技术六届五次全国学术交流会, 阿尔山市, 2014. |
| [12] | 郭洪涛, 刘靖, 吕彬彬, 等.连续变速压颤振试验数据处理方法研究[C]//第14届中国系统仿真技术及其应用学术年会, 三亚市, 2012. |
| [13] | 何彬华, 凌忠伟, 胡向鹏, 等. FL-23风洞级间分离与网格测力试验系统[J]. 实验流体力学 , 2013, 27 (4) : 109–112. He B H, Ling Z W, Hu X P, et al. The stage separation and proximity matrix test in FL-23 wind tunnel[J]. Journal of Experiments in Fluid Mechanics , 2013, 27 (4) : 109–112. |
| [14] | 郭洪涛, 路波, 余立, 等. 某战斗机高速全模颤振风洞试验研究[J]. 航空学报 , 2012, 33 (10) : 1765–1771. Guo H T, Lu B, Yu L, et al. Investigation on full-model flutter of a certain fighter plane in high-speed wind tunnel test[J]. Acta Aeronautica et Astronautica Sinica , 2012, 33 (10) : 1765–1771. |
| [15] | 郭洪涛, 路波, 吕彬彬, 等.面向紊流激励响应的颤振亚临界预测方法[C]//第十三届系统仿真会议, 黄山市, 2011. Guo H T, Lu B, Lyu B B, et al. A subcritical prediction of flutter onset for excitation response based on airstream turbulence[C]. The 13th System Simulation Technology & Application, Huangshan:2011. |



