2. 中国计量学院, 杭州 310018
2. China Jiliang University, Hangzhou 310018, China
由于具有较大比表面积、高效热质交换效率等特点,近年来微柱群结构常用于设计制作微混合器和微换热器[1-2]。作为一类特殊结构的微流控芯片,微柱群也在生命科学和疾病诊断中得到了应用,用来模拟生物多孔介质以及肿瘤细胞的捕获与检测等[4-6]。大尺度条件下柱群绕流问题已经得到了广泛研究,但微柱群绕流的研究却非常有限。过去15年中,显微粒子图像测速技术(Micro-PIV)已经广泛应用于微流体全场可视化测量中,为研究复杂微流动奠定了重要基础[7]。
在Micro-PIV测量中,为减小示踪粒子布朗运动对速度场测量精度的影响,在传统互相关分析的基础上提出了平均相关算法(Correlation Averaging),目前已经成为重要的速度分析算法[8]。然而,由于Micro-PIV采用的体照明方法,所有成像粒子都将在相关函数的计算中起作用,因此相关深度(Depth of Correlation,简写为DOC)的概念被提出,并成为影响速度计算准确性的一个重要参数[9-10]。由于相关深度的影响,不仅焦平面内(简称为“面内”)粒子参与互相关计算,焦平面以外(简称为“面外”)的粒子图像也将对互相关函数有所贡献,并影响到相关峰值的位置,从而引起速度场评估的误差[11]。
近年来,随着Micro-PIV技术应用范围的进一步扩大,研究领域涉及到复杂流动区域的流动问题。诸如针对生物微流体、芯片实验室流动以及多孔介质内流等流场测量问题,需要在较宽的流动区域充分揭示流动结构的全貌。此时Micro-PIV测量需要选择小倍率、大视场物镜,由此实现较宽视场内的流动测量。对于此类物镜,由于放大倍率小,可选择粒径较大(如微米量级)的示踪粒子,测量中布朗运动效应将显著减小。但由于小倍率物镜通常具有大景深,体照明方式会造成大量的面外粒子在相机芯片上成像,成为大相关深度测量,即便采用平均相关技术进行速度场计算,仍然会造成较大的测量误差。虽然被测平面外的粒子能够通过背景噪音去除、阈值过滤等图像处理方法被有效去除,但粒子图像密度随之减小。为了能够获得准确的速度场,需要采用粒子图像叠加方法达到满足互相关分析要求的粒子图像密度,因此低密度粒子图像叠加法[11]成为针对小倍率、大视场Micro-PIV测量问题的重要方法,能够有效减小相关深度,提高速度测量准确性[12-13]。
本文在分析相关深度对速度测量影响的基础上,将低密度粒子图像叠加技术应用于微柱群绕流流场的分层测量中。对于每个流体平面,采用一定数量的图像在预处理的基础上进行叠加处理,在满足粒子图像密度基础上采用互相关算法进行速度场分析。为了验证测量的准确性,将该速度测量结果与采用平均相关算法的结果进行比较。
1 低密度粒子图像叠加方法 1.1 相关深度对速度测量的影响Micro-PIV测量的相关深度被定义为从物镜焦平面到另一个平面距离的2倍。该平面的选择原则是规定其图像强度为焦平面上图像强度的某一个百分数ϕ[14]。换言之,如果图像灰度比值高于ϕ值,则示踪粒子在相关深度范围内;如果低于ϕ值,则示踪粒子不在相关深度范围内。因为速度测量是通过粒子图像的相关函数来计算的,因此可以认为此时粒子的图像灰度不会对速度的测量产生重要影响。
由于Micro-PIV测量会受到相关深度的影响,测量平面外(简称面外,Out-of-plane)的粒子图像对相关函数的贡献造成了速度场测量值Vmeas偏离真实值Vreal,由此将影响由覆盖全流场不同流体平面二维速度构建的三维全场的准确性,该影响对于剪切流场尤为显著。图 1所示为剪切流场壁面和峰值速度平面受平面外粒子灰度所获相关峰值影响的示意图。图 1(a)说明,实测相关峰值的位移受到了该流体平面外示踪粒子相关峰值位移的影响,造成近壁区的速度高于真实的速度,由此解释了Micro-PIV近壁区的测量速度通常都表现出滑移流的主要原因。但该滑移速度并非真实的滑移速度,称之为“伪滑移速度”。图 1(b)表明,由于速度峰值平面外的速度均小于该平面速度,造成实测相关峰值位移降低,因此峰值平面的实测速度通常小于真实的速度。

|
| 图 1 相关深度对相关函数的影响示意图。(a)近壁区相关峰值的正偏差,出现“伪滑移速度”; (b)中心层平面相关峰值的负偏差。图中±Δx为位移偏差; Φ, ΦS及ΦB分别为总相关函数, 焦平面粒子及背景粒子图像对相关函数的贡献; Vmeas及Vreal分别为速度测量值和真实值。 Fig.1 The influence of DOC on the correlation function. (a) Positive deviation of correlation peak near wall surface, "pseudo-slip flow"; (b) Negative deviation of correlation peak on center plane. where±Δx is the displacement deviation; Φ, ΦS and ΦB are the total correlation function and correlation function contributed by in-plane particle images and background particle images, respectively; Vmeas and Vreal are the measurement value and real value of velocity, respectively. |
为了提高因相关深度造成的三维速度场测量不准确的问题,需最大限度减小相关深度。因此通过图像处理方法去除被测流体平面以外的粒子图像,有效减小相关深度,达到消除相关函数峰值漂移,提高速度场测量的准确性,而采用低密度粒子图像叠加技术成为实现该目标的一类行之有效的方法[11]。
1.2 低密度粒子图像叠加方法低密度粒子图像叠加方法与早期采用单帧多曝光图像采集技术用来增加PIV图像中的粒子数相类似,是通过计算创造一定数量的低粒子密度PIV图像的叠加,图像灰度值采用下式计算,
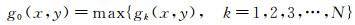 (1)
(1)
式中:gk(x, y)是一组低密度粒子图像序列下第k(1~N)个图像的灰度分布,g0(x, y)是叠加后的图像灰度值分布[12]。此式表明在进行低密度粒子图像叠加操作时,取灰度值最大的一组粒子图像作为叠加对象。
对于体照明方式,粒子图像灰度(服从二维高斯函数)峰值通常随远离焦平面距离的增加递减,因此Micro-PIV粒子图像中具有最大灰度的粒子图像通常是位于焦平面上的粒子图像。因此式(1)运算的结果是一个时间序列上采集的所有粒子图像中焦平面(被测平面)上的粒子得以保留,其他平面的粒子图像被有效去除,从而实现该序列的粒子图像叠加。由于焦平面以外的粒子图像被剔除,在进行操作的过程中将相关深度控制在焦平面附近,因此消除了背景粒子对相关函数的贡献,最大限度地提高了被测平面速度评估的准确性。
将式(1)应用于实际采集的低密度粒子图像时,需要经过背景噪音去除、灰度阈值过滤和图像增强等图像处理过程,其流程如图 2所示。其中背景噪声去除的主要目的是消除由CCD相机热噪声带来的背景灰度;阈值过滤则是通过设置最大灰度的阈值剔除被测平面外的粒子图像,相当于式(1)中单个图像的最大值运算;图像增强是在前两者基础上,对保留在图像中的粒子灰度值进行放大,增强对粒子的识别能力。对一个时间序列的所有图像进行上述操作后,即进行低密度粒子图像叠加处理,直到图像密度满足互相关分析的要求。在选择叠加的图像数量时,采用如下准则:如果示踪粒子原溶液与水的体积比为1:N(N>>1),则可采用N个低密度粒子图像进行叠加,由此叠加后的粒子图像密度能满足采用互相关技术的速度场分析[16]。需要说明的是,本文的方法是针对美国Thermo Scientific公司提供的荧光粒子原溶液提出的数据,如采用其他公司的荧光粒子,需通过实验进行确定。
为了验证该方法的可行性,开展了长直微通道中间层速度测量的验证实验。实验系统由Nd :YAG双脉冲激光器(美国New Wave公司),图像增强型CCD相机,分辨率为1376pixel×1024pixel,LD Plan-Neofluar型显微物镜,放大倍率和数值孔径为20×0.40NA (德国Carl Zeiss)。采用具有精确调节三维坐标功能的显微平台实现流体分层测量,垂向最高分辨率达到100nm,测量系统原理如图 3所示。

|
| 图 3 测量系统原理图 Fig.3 Particle image between micro-cylinder arrays |
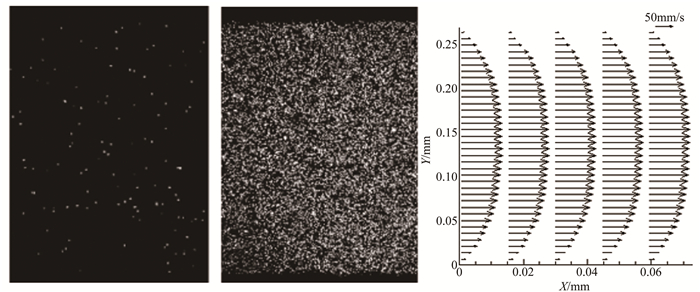
将示踪粒子原溶液和去离子水按照体积比为1:100进行混合稀释,配置低浓度的示踪粒子溶液进行图像采集,采集频率为10Hz。采用Bitsch等人[17]提出的灰度过滤方法进行阈值过滤,经试验发现阈值取为20时能够得到无背景噪声且几乎不失真的粒子图像。在此基础上进行图像增强处理,所获单幅图像如图 4(a)所示。由于示踪粒子溶液按照1:100进行配比,根据上述叠加准则,选取100对低密度粒子图像进行叠加,获得的叠加粒子图像如图 4(b)所示。能够看到叠加后的粒子图像无论是灰度的一致性还是粒子图像密度均达到了较为理想的图像质量。经过互相关分析,获得了准确的速度矢量,如图 4(c)所示。
|
| 图 4 低密度粒子图像叠加方法计算速度场 Fig.4 Velocity calculation by the image overlapping |
被测微柱群通道由PDMS材料加工而成。柱群为错列分布,直径为40μm。展向和流向相邻圆柱间的圆心距分别为60和80μm。为获得低密度粒子图像,将1μm荧光示踪粒子(美国Thermo Scientific公司生产)与去离子水按1:100比例混合后由注射泵注入微通道。将通道由底部到顶部分为12个流体层,利用三维坐标平台进行垂直方向的调节,间隔4μm。图 5给出了典型低密度粒子的原始图像。

|
| 图 5 微柱群粒子图像 Fig.5 Particle image between micro-cylinder arrays |
以圆柱直径D为特征尺寸,以通道截面的平均速度U为特征速度,设定0.8~3.6等8个雷诺数,间隔为0.4,由此反算注射泵的输入流量Q,如式(2)所示。
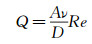 (2)
(2)
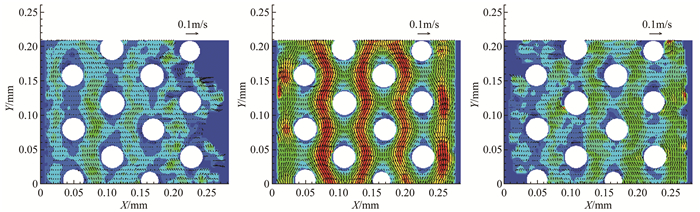
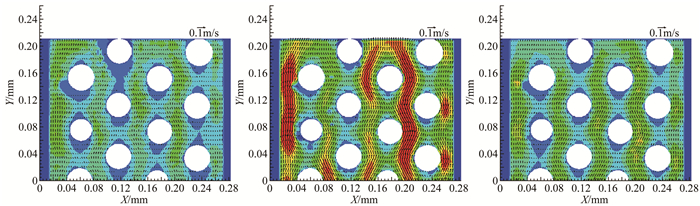
式中:A为通道截面面积,ν为运动粘性系数,D为圆柱直径。对12层流体平面的叠加图像进行互相关分析,得到由底面到顶面一组二维速度场。同时为了评估低密度粒子图像叠加方法,开展了一组采用平均相关算法的实验,示踪粒子溶液与水的体积比为1:10。作为示例,图 6和7分别给出了采用2种方法获得的底层、峰值速度层和顶层速度场测量结果(Re=0.4),其中图 6为采用低密度粒子图像叠加方法的结果,图 7为采用平均相关算法的结果。子图(a)~(c)分别为底面、峰值速度平面及顶面速度场测量结果。
|
| 图 6 采用低密度粒子图像叠加方法获得的分层速度场分布 Fig.6 Velocity on multi-fluid planes by image overlapping method |
|
| 图 7 采用平均相关法获得的分层速度场分布 Fig.7 Velocity on multi-fluid planes by correlation averaging method |
测量结果显示,相比传统的平均相关算法,采用低密度粒子图像叠加方法所获速度场更合理。从顶面和底面的速度场,即对应子图(a)和(c)的比较可以看到,采用低密度粒子图像测速方法所获壁面速度更接近无滑移,其速度明显低于平均相关算法的结果。此外,由于速度测量精度的提高,上下表面的粗糙度等因素也能通过速度场分布的复杂性体现出来,而传统平均相关方法将表面形貌对速度场的影响抹平,给出了几乎均匀的速度分布,显然与真实的近壁区流场存在较大偏差。
对于峰值速度流体层,2种方法测量结果也存在显著差异。从图 6(b)给出的流场结构可以看到,基于低密度粒子图像叠加法的结果流场呈现出低速绕流周期性特征,且高、低速度区分布合理。而反观图 7(b),采用平均相关算法计算的速度场却未能给出合理的速度分布,高速和低速区的分布无明显规律可寻,可见其速度测量精度远低于前者。
2.3 空间平均速度廓线为了进一步比较两者的速度测量结果,按照式(3)对每一层的速度进行空间平均,获得空间平均速度(Spatial Averaged Velocity, SAV),从而得到全部12个流体平面速度构成的空间平均速度廓线。
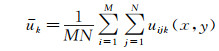 (3)
(3)
式中:u k为第k(k=1~12)个流体层的空间平均速度;M和N分别为流向和展向的判读域总数;uijk(x, y)为第k个流体层的流向速度分布函数,其中下标i(i=1~M)和j(j=1~N)分别表示判读域在流向和展向的编号。
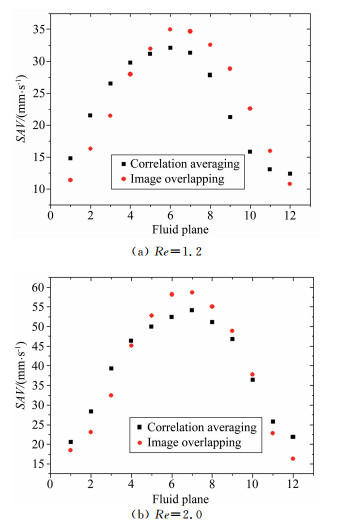
利用式(3)对所有8个雷诺数采用2种方法获得的空间平均速度进行比对。作为示例,图 8给出了Re数分别取1.2和2.0的结果,其他Re数也有类似结果。图中,正方形点为采用平均相关方法的结果,圆点表示低密度图像叠加方法的结果。
|
| 图 8 空间平均速度廓线 Fig.8 Profiles of spatial averaged velocity |
可以看到,两者都呈现“类抛物线”分布,但两者速度值存在明显差异。以近壁区和中间层为例进行说明:对于近壁区,虽然2个结果都存在“伪滑移速度”,但采用低密度粒子叠加方法得到的近壁区空间平均速度小于采用平均相关算法的结果,后者有更显著的“伪滑移速度”。值得说明的是,采用低密度粒子图像测速方法之所以也出现了“伪滑移速度”,其主要原因与壁面结构以及定位的精度有关,而非相关深度的影响。事实上,经过阈值过滤后,面外粒子图像已经基本被剔除,相关深度影响基本可以忽略。对于峰值速度,能够看到采用低密度粒子叠加方法所测速度值高于平均相关算法。以上结果与图 1给出的分析是一致的。
为了定量说明底面、顶面及峰值测量速度的差异,根据空间平均速度,定义一个无量纲壁面滑移速度VNDS,如式(4)所示。
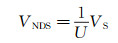 (4)
(4)
式中:U为截面平均速度,可见表 1给出的数据;VS为测量的壁面滑移速度,即“伪滑移速度”。以平均相关算法所获壁面滑移速度为基准,计算低密度粒子图像叠加方法的相对偏差δS如下:
| Re | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 平均值 |
| Q/(μl·s-1) | 14.3 | 21.5 | 28.6 | 35.8 | 42.9 | 50.1 | 57.2 | 64.4 | / |
| 底面VS, a/(mm·s-1) | 8.6 | 14.7 | 18.7 | 20.5 | 27.3 | 25.6 | 36.0 | 37.1 | / |
| 底面VNDS, a | 0.43 | 0.49 | 0.47 | 0.41 | 0.46 | 0.37 | 0.45 | 0.41 | 0.44 |
| 底面VS, o/(mm·s-1) | 5.4 | 11.5 | 12.5 | 18.4 | 21.2 | 17.6 | 30.4 | 33.5 | / |
| 底面VNDS, o | 0.27 | 0.38 | 0.31 | 0.37 | 0.36 | 0.25 | 0.38 | 0.37 | 0.34 |
| 底面δS/% | -37.2 | -21.8 | -33.2 | -10.2 | -22.3 | -31.3 | -15.6 | -9.7 | -22.7 |
| 顶面VS, a/(mm·s-1) | 10.6 | 12.3 | 12.6 | 21.9 | 21.3 | 28.9 | 29.5 | 37.6 | / |
| 顶面VNDS, a | 0.53 | 0.41 | 0.32 | 0.44 | 0.36 | 0.41 | 0.37 | 0.42 | 0.41 |
| 顶面VS, o/(mm·s-1) | 9.1 | 10.7 | 13.5 | 16.3 | 13.8 | 20.5 | 23.2 | 35.1 | / |
| 顶面VNDS, o | 0.46 | 0.36 | 0.34 | 0.33 | 0.23 | 0.29 | 0.29 | 0.39 | 0.34 |
| 顶面δS/% | -14.2 | -13.0 | 7.1 | -25.6 | -35.2 | -29.1 | -21.4 | -6.6 | -17.2 |
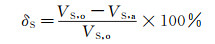 (5)
(5)
式中:VS, o和VS, a分别为采用粒子图像叠加方法和平均相关算法所得到的壁面滑移速度。针对底面和顶面分别进行了计算,结果由表 1给出。
如表 1所示数据,随Re数增加,“伪滑移速度”数值总体上有增加趋势(除个别点外),表明随着主流速度增加,相关深度范围内面外粒子位移呈现增大趋势。基于平均相关算法的底面无量纲滑移速度在0.37~0.49之间变化,顶面结果介于0.32~0.53之间,2个壁面的平均无量纲滑移速度值分别为0.44和0.41;基于低密度粒子图像叠加方法的底面无量纲滑移速度值在0.25~0.38之间,顶面结果介于0.23~0.46之间,相应的平均值均为0.34。底面和顶面的相对速度偏差分别为-22.7%和-17.2%,表明基于低密度粒子图像叠加方法的“伪滑移速度”得到了较好的控制。
采用同样的处理方法,无量纲峰值速度VNDP及相对偏差δP分别由式(6)和(7)给出:
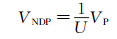 (6)
(6)
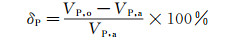 (7)
(7)
式中:VP为测量所得峰值速度,VP, o和VP, a分别为基于低密度粒子图像叠加方法和平均相关算法的峰值速度。相应的计算结果由表 2列出。
| Re | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 平均值 |
| Q/(μl·s-1) | 14.3 | 21.5 | 28.6 | 35.8 | 42.9 | 50.1 | 57.2 | 64.4 | / |
| VP, a/(mm·s-1) | 24.2 | 31.7 | 46.3 | 54.1 | 66.3 | 75.3 | 89.5 | 98.2 | / |
| VNDP, a | 1.22 | 1.06 | 1.16 | 1.09 | 1.11 | 1.08 | 1.12 | 1.10 | 1.12 |
| VP, o/(mm·s-1) | 24.7 | 35 | 45.8 | 58.7 | 72.2 | 78.9 | 93.8 | 101.3 | / |
| VNDP, o | 1.24 | 1.17 | 1.15 | 1.18 | 1.21 | 1.13 | 1.18 | 1.13 | 1.17 |
| δS/% | 2.1 | 10 | -1.1 | 8.5 | 8.9 | 4.8 | 4.8 | 3.2 | 5.2 |
如表 2所示,基于平均相关算法和低密度粒子图像叠加方法的无量纲峰值速度平均值分别为1.12和1.17,后者高于前者,相对偏差约为5.2%。
3 结论本文对Micro-PIV低密度粒子图像叠加方法进行了研究,将其应用于微柱群绕流的速度场测量,并与传统的平均相关算法进行了比较。结论如下:低密度粒子图像叠加法有利于减少相关深度(DOC),能够提高速度测量的准确性。实验结果表明,通道底部和顶部近壁区的平均“伪滑移速度”分别减小了22.7%和17.2%,通道中心平均速度峰值增加了5.2%。底面和顶面的“伪滑移速度”得到了较好的改善;峰值速度没有受到测量层以外相对低速粒子的干扰接近真实速度。
| [1] | Yoshida H. The wide variety of possible applications of micro-thermofluid control[J]. Microfluid Nanofluid , 2005, 1 : 289–300. DOI:10.1007/s10404-004-0014-7 |
| [2] | Yeom J, Agonafer D D, Han J H, et al. Low Reynolds number flow across an array of cylindrical microposts in a microchannel and figure-of-merit analysis of micropost-filled microreactors[J]. J Micromech Microeng , 2009, 19 : 065025. DOI:10.1088/0960-1317/19/6/065025 |
| [3] | Tamayol A, Khosla A, Gr ay, et al. Bahrami creeping flow through ordered arrays of micro-cylinders embedded in a rectangular minichannel[J]. Int J Heat Mass Transfer , 2012, 55 (15-16) : 3900–3908. DOI:10.1016/j.ijheatmasstransfer.2012.03.008 |
| [4] | Wang D M, Tarbell J M. Modeling interstitial flow in an artery wall allows estimation of wall shear stress on smooth muscle cells[J]. J Biomech Eng , 1995, 117 : 358–363. DOI:10.1115/1.2794192 |
| [5] | Tada S, Tarbell J M. Interstitial flow through the internal elastic lamina affects shear stress on arterial smooth muscle cells[J]. Amercian Journal of Physiology-Heart and Circulatory , 2000, 278 : 1589–1597. |
| [6] | Nagrath S, Sequist L V, Maheswaran S, et al. Isolation of rare circulating tumour cells in cancer patients by microchip technology[J]. Nature , 2007, 450 : 1235–1239. DOI:10.1038/nature06385 |
| [7] | Santiago J G, Wereley S T, Meinhart C D. A particle image velocimetry system for microfluidics[J]. Exp Fluids , 1998, 25 (4) : 316–319. DOI:10.1007/s003480050235 |
| [8] | Wereley S T, Meinhart C D. Recent advances in micro-particle image velocimetry[J]. Annu Rev Fluid Mech , 2010, 42 : 557–576. DOI:10.1146/annurev-fluid-121108-145427 |
| [9] | Wereley S T, Meinhart C D, Gray M H B. Depth effects in volume illuminated particle image velocimetry[C]. The Third International Workshop on Particle Image Velocimetry, Santa Barbara, 1999:545-550. |
| [10] | Olsen M G, Adrian R J. Out-of-focus effects on particle image visibility and correlation in microscopic particle image velocimetry[J]. Exp Fluids , 2000, 29 : S166–S174. DOI:10.1007/s003480070018 |
| [11] | Chuong V, Nguyen A F, Josie C. Improvement of measurement accuracy in micro PIV by image overlapping[J]. Exp Fluids , 2010, 49 : 701–712. DOI:10.1007/s00348-010-0837-9 |
| [12] | Wereley S T, Gui L, Meinhart C D. Advanced algorithms for microscale particle image velocimetry[J]. AIAA J , 2002, 40 : 1047–1055. DOI:10.2514/2.1786 |
| [13] | Massimiliano R, Rodrigo S, Christian C, et al. On the effect of particle image intensity and image preprocessing on the depth of correlation in micro-PIV[J]. Exp Fluids , 2012, 52 : 1063–1075. DOI:10.1007/s00348-011-1194-z |
| [14] | 王昊利, 王元. Micro-PIV--粒子图像测速技术的新进展[J]. 力学进展 , 2005, 35 (1) : 77–90. Wang H L, Wang Y. Micro-PIV--the new trend of Particle Image Velocimetry[J]. Advance in Mechanics , 2005, 35 (1) : 77–90. |
| [15] | Nam-Trung N, Steven T, Wereley S T. Fundamentals and applications of microfluidics[M]. Artech House, Inc: , 2002 . |
| [16] | 徐明, 王昊利. 基于低密度粒子图像叠加的Micro-PIV速度场测量[J]. 实验流体力学 , 2013, 27 (2) : 106–112. Xu M, Wang H L. The micro-PIV measurement based on the low particle density[J]. Journal of Experiments in Fluid Mechanics , 2013, 27 (2) : 106–112. |
| [17] | Bitsch L, Olesen L, Westergaard C, et al. Micro particle-image velocimetry of bead suspensions and blood flows[J]. Exp Fluids , 2005, 39 : 507–513. DOI:10.1007/s00348-005-0967-7 |




