2. 中煤科工集团武汉设计研究院有限公司 管道输煤所, 武汉 430070
2. Department of Pipeline Coal Transporting, Wuhan Design and Research Institute of China Coal Technology and Engineering Group, Wuhan 430064, China
随着浆体管道输送技术的发展,越来越多的行业和部门要用到物料的管道输送技术,如水力采煤、海洋采矿、地面金属矿管道输送、水库河流清淤和地面管道输煤等。在特定条件下,如地势起伏不平,或者管道容易受到外界干扰时,就要涉及到倾斜管道浆体输送技术。倾斜向上管道输送中,淤积临界流速和速度分布的研究对于倾斜浆体管道输送的参数优化、堵塞的防止以及输送成本的降低都有重要意义。
近5年来,国内外浆体管道输送技术中,淤积临界速度的研究主要集中在水平管道方面[1-15]。这些研究均着眼于水平管道流动,未能考虑管道角度的因素。此外,上述关于淤积临界流速的研究基本上是从单个颗粒受力考虑的,而不是从群体颗粒角度考虑。为了便于研究,本文中的淤积临界速度指的是管道底部固体颗粒全部开始滑动时的浆体平均流速。滑动底床流动是管道中颗粒由静止转入运动的过渡形式之一,与淤积临界流速有密切的关联,其在倾斜管道试验中被多次观测到[16-17]。因而,要确定固体颗粒管道输送的临界淤积条件,一般需要对滑动底床的运动进行研究(实际管道输送中, 出现层移运动的可能性较小)。迄今为止,伴有滑动床的倾斜管道浆体流动方面的研究主要集中于阻力损失和床上方浓度分布方面[18-20]。而滑动床上方速度分布的研究也未见公开发表。可见,从滑动床运动角度考虑倾斜浆体管道淤积临界速度和速度分布的研究国内外尚无记载。而粗颗粒滑动床输送形式在工程中的应用越来越多,因此,有必要开展这方面的研究。
1 滑动床厚度求解模型的推导在倾斜管道中建立坐标系,以沿着管道轴线倾斜向上方向为x轴,以垂直于管道轴线向上方向为y轴,垂直主流方向,距离管道底部y处颗粒体积浓度为Sv。众多研究表明,在固液两相流中,固体颗粒的浓度是随高度的变化而变化的,流动参数只在y方向发生变化[21-22]。根据紊流扩散理论,可以得到[20]:
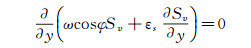 (1)
(1)
考虑边界条件并对式(1)进行积分,结果为:
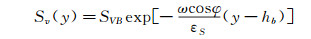 (2)
(2)
对式(2)积分,可以求得悬浮层的平均浓度公式为:
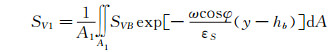 (3)
(3)
式中:SV1为悬浮层(上层)的平均体积浓度;SVB为下层(滑动层)的平均体积浓度;A1为管道中悬浮层所占的面积;εs为固体颗粒的扩散系数,其计算方法见有关文献[20]。
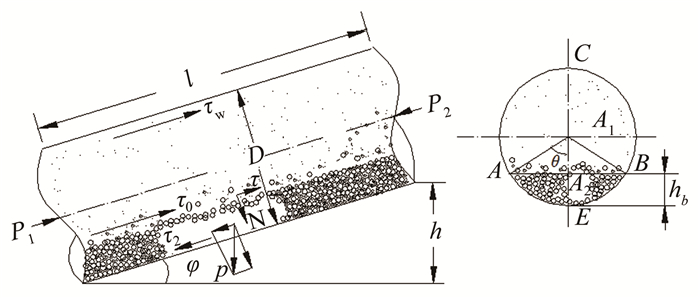
设倾斜管道内浆体的平均体积浓度为SV;下层(滑动层)的平均体积浓度为SV2(等于SVB);下层断面积为A2;上层的平均流速为U1;下层的平均流速为U2;P1和P2为长度为l的管段两边的压力,如图 1所示。
|
| 图 1 浆体倾斜管道流动示意图 Fig.1 Schematic diagram of slurry pipe flow in inclined pipe |
根据颗粒和液体质量守恒,可以得到:
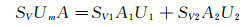 (4)
(4)
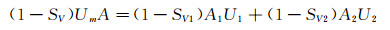 (5)
(5)
设所研究的浆体管道长度为l,垂高为h;管道上部内壁与浆体之间的剪应力为τw;滑动床上部浆体与滑动床之间的剪应力为τ0;管道下部滑动床内部流体与管壁之间的剪应力为τ2。对于滑动床上部浆体,当其处于均匀流动时,根据力的平衡条件,如图 1所示,有:
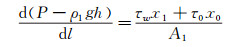 (6)
(6)
式中:x1为圆弧ACB长度;x0为弦AB的长度,P为长度为l为管段两边的压力差(即P1-P2)。根据图 1,x1和x0可以分别表示为:x1=D(π-θ),x0=Dsinθ。其中D为管道直径, θ为滑动床中心角。
式(6)可以变为:
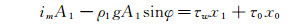 (7)
(7)
ρ1、τw和im的计算见文献[23]。
式(7)中剪应力τ0计算公式为:
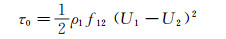 (8)
(8)
式中:f12为悬浮层和滑动床间界面的阻力系数, 此处采用C.A.Shook和M.C.Roco提出的公式[24]:
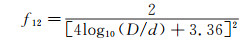 (9)
(9)
式中:d为颗粒平均粒径。
将式(3)、(4)、(5)和(7)联合组成方程组求解,可以求解出滑动床厚度hb,以及U1、U2和SV1。
为了验证通过式(3)、(4)、(5)和(7)联合组成方程组求解hb、U1、U2和SV1迭代方法的收敛性,进行了颗粒平均粒径为1.71mm浆体的水平管道和倾角为30°倾斜管道的试算,输送浓度CVd为0.21,浆体平均速度为5.5m/s。利用Matlab软件编制了迭代法求解非线性方程组的程序,设置求精度为0.001,迭代20次后,所求解量与迭代次数n的关系如图 2所示。
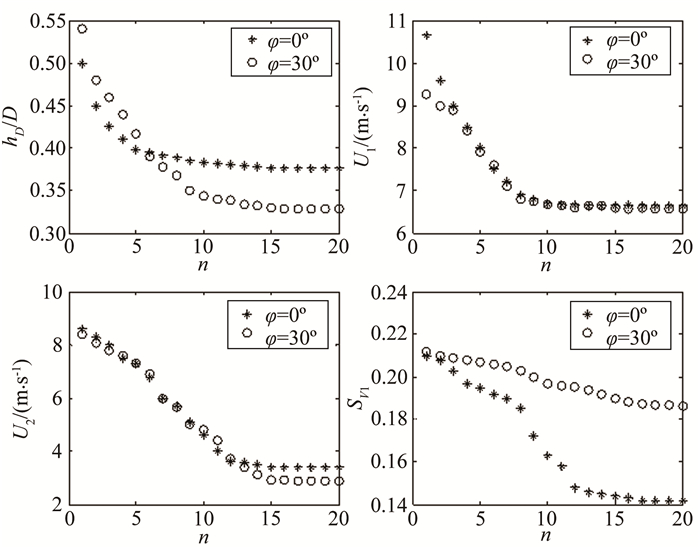
|
| 图 2 迭代次数n与各变量的关系 Fig.2 Relation between the iteration number and the variables |
从图 2各变量随迭代次数变化的曲线可以看出,计算结果收敛。这说明,通过式(3)、(4)、(5)和(7)联合组成方程组求解hb、U1、U2和SV1是可行的。
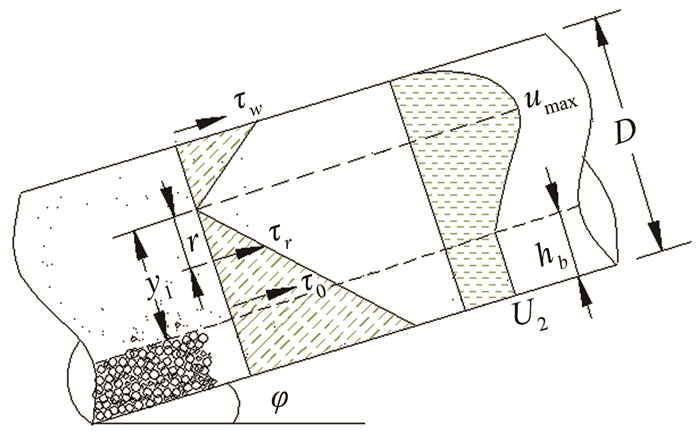
2 滑动床上方速度分布模型的推导浆体管道输送时,上层浆体紊流流动时,剪应力一般呈现k型分布,如图 3所示。剪应力τ0和上部剪应力τw可以通过计算得到。根据图 3可知,浆体悬浮层流动时,存在剪应力为零的点,由对称性可知,零剪力点一定在断面的中垂线上,且是最大流速umax的所在位置[25]。假定滑动床上方垂向剪应力呈线性分布,零剪应力点在滑动床面以上y1处。则根据图 3所示,可以得到:
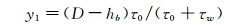 (10)
(10)
|
| 图 3 伴有滑动床的倾斜管道速度分布和剪应力分布示意图 Fig.3 Schematic diagram of velocity distribution and shear stress distribution of inclined slurry pipe with sliding bed |
最大速度可用以下各式求解[26]:
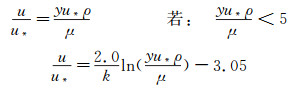 (11)
(11)
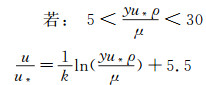 (12)
(12)
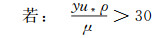 (13)
(13)
上面3式中,ρ为清水密度,u为清水的动力粘性系数,u *为剪切速度, 计算式为:
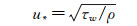 (14)
(14)
求得最大速度umax后,利用任意点剪切应力τr与普朗特半经验公式得到的剪应力相等,可以得到速度分布计算公式为:
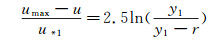 (15)
(15)
式中:r为距离最大速度点的垂直距离;u* 1为当地剪切速度,k为卡门常数,取值为0.4;u* 1的计算公式为[26]:
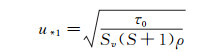 (16)
(16)
式中:Sv为任意点体积浓度,S为固体颗粒比重,ρ为清水密度。Sv可以通过式(2)确定。
3 倾斜管道中临界速度求解模型推导以倾斜管道中滑动床为研究对象,如图 1所示,当滑动床处于受力平衡状态时,设τ为滑动床上方处于跳动的颗粒对于滑动床的碰撞力沿着管道轴方向的分量,N为碰撞力垂直于管轴的分量。使滑动床保持受力平衡时的速度就是管道颗粒淤积的临界速度。此时,使滑动床移动的动力Fd为:
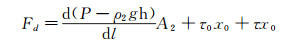 (17)
(17)
阻止滑动床移动的阻力Fz为:
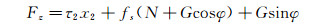 (18)
(18)
式中:x2为圆弧AEB长度;fs为滑动床与管道壁间的摩擦系数;G为滑动床水下的有效重力,其表达形式为:
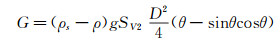 (19)
(19)
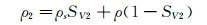 (20)
(20)
通常,认为τ和N很小,因而τ和N在此可以忽略。再考虑到τ2是滑动床内部流体与管壁之间的剪应力,可认为近似与上部浆体与管壁的剪应力τw相等,则式(17)和(18)可以分别简化为:
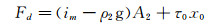 (21)
(21)
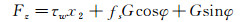 (22)
(22)
因而淤积临界速度具体求解方法步骤为:
(1)令浆体初始的平均速度Um(0)足够大,使管道底部无静止颗粒层存在;
(2)k为用于计算次数的整数,开始k=1;
(3)Um(k)=Um(k-1)-ΔUm,ΔUm为一微小的速度增量;
(4)将式(3)、(4)、(5)和(7)组成方程组,联合求解出hb、U1、U2和SV1;
(5)利用式(21)和(22)分别计算滑动床所受的动力Fd和阻力Fz;
(6)若Fd>Fz,则k=k+1,返回步骤(3),重复(3)~(6)各步, 否则计算结束;
(7)最后得到的Um(k-1)即为淤积临界流速度Udl。
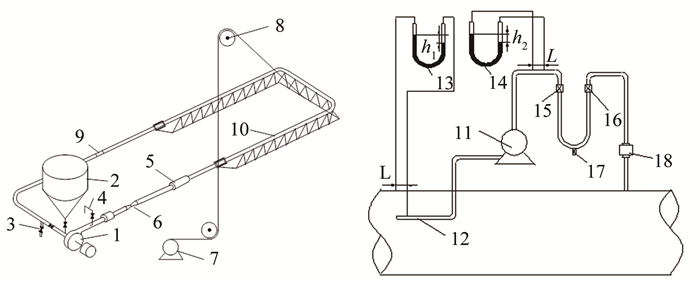
4 实验研究 4.1 实验装置总体描述试验总体管路布置如图 4所示,管路总体长度40m左右。为了减少测量误差,试验中采用了等动力探头及样品旁路管路装置,如图 4右侧所示[27]。为了能够改变测量管路的倾角,采用电机7、滑轮8,将测试管段吊起,从而改变管路倾角。
|
| 图 4 试验管路布置及等动力测量装置布置图 Fig.4 Layout of test pipeline and isokinetic measuring pipe 1浆体泵; 2浆体罐子; 3泄流阀; 4流量取样; 5热交换器; 6缩颈阀; 7电机; 8滑轮; 9亚克力透明管; 10测试管段; 11旁路浆体泵; 12探头; 13, 14压差计; 15, 16阀门; 17排泄阀; 18流量计 |
根据伯努利方程,当图 4中水头损失h1等于h2时,管道中的浆体流速与采样头12中的流速相同,此时测量比较准确。等动力学采样探头12可以旋转,因此可以在管道横断面内任一点取样。当水头损失h1等于h2时,阀门15和16之间的浆体样本与管道内浆体误差最小。此时关闭阀门15和16,通过排泄阀17获得一定体积的浆体样本。对获取的浆体样本进行处理,可以得到干燥的固体颗粒体积及颗粒级配,进而得到浆体的各个测量点当地浓度。通过流量取样阀4排出的浆体样本,可以得到输送浓度CVd的值。浆体各个测量点流动速度可通过流量计18得到。在透明有机玻璃管段,采用JVC GZ-N1PAC高清闪存摄像机拍摄颗粒在管道内的滑动床运动状态图像。来自于浆体罐2的浆体通过浆体泵1加压,进入测试管段10。
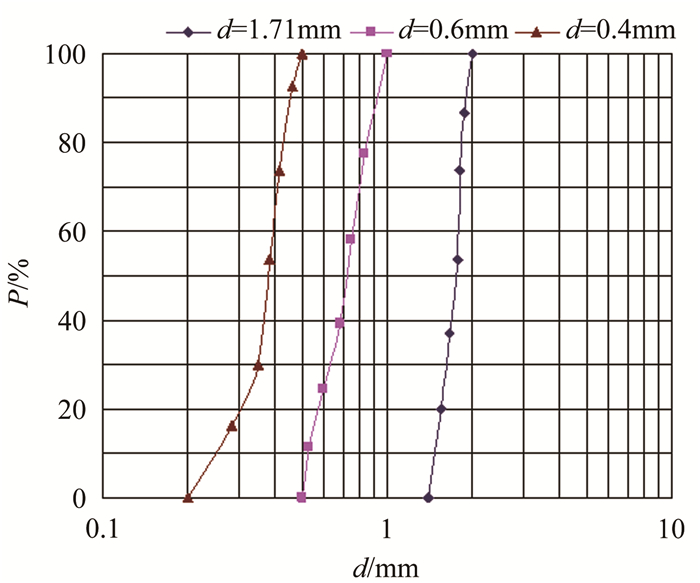
试验中采用砂颗粒平均粒径分别为0.4、0.6和1.71mm,颗粒的级配情况如图 5所示,3种颗粒均级配均为窄级配分布。粗砂颗粒密度为2650 kg/m3,形状为近似球形。
|
| 图 5 颗粒级配曲线 Fig.5 Map of particle size distribution |
测试段管道内径为150mm,管道倾角分别为0°、10°、16°、20°、25°和30°。浆体浓度变化范围为0.10~0.27。测试中将管道中心点O上、下各划分为4个条带,从而需要测定9个点的浓度值(假定各条带内颗粒浓度均匀)。透明有机玻璃测试管段的直径为150mm,长度为460mm,用来观测不同角度及流动状态。管道内浆体的平均体积浓度SV通过对浓度分布进行积分而得到。
试验中,通过连续调整浆体平均速度Vm,观测和记录管道底部颗粒运行状态。当管道底部滑动床从连续运动状态即将进入静止状态时,记录此时对应的平均速度Um,即为淤积临界速度值。经过试验确定,颗粒滑动床内浓度SVB近似为一常数,约0.5左右,固定床浓度大致为0.6左右。管道与粗砂颗粒间的滑动摩擦系数fs为0.55左右。
4.3 图像采集与分析用高速摄影机测量浆体管道中不同运动状态时,颗粒床的厚度和运动速度等信息。拍摄的图像蕴含颗粒运动信息。试验时,通过逐渐增大浆体流速,同时拍摄颗粒群体管道中运行状态。摄像机最高拍摄速度为6×105帧/s,镜头分辨率为2350pixel×900pixel。摄像机通过usb接口将图像一幅一幅地传输到电脑中进行信息分析,从而确定各个流速下是否存在滑动床,以及床高度和速度等信息。
4.4 不同工况条件水平管道中的淤积临界流速度测试试验工况如表 1所示;倾斜管道中测试不同倾角下的淤积临界流速度以及淤积时床角度和管道倾角关系的试验工况如表 2所示。
| 第1组 | 第2组 | 第3组 |
| d=0.4mm | d=0.6mm | d=1.71mm |
| CVd=0.11~0.36 | CVd=0.09~0.33 | CVd=0.08~0.24 |
| 第1组 | 第2组 | 第3组 |
| d=0.4mm | d=0.6mm | d=1.71mm |
| CVd=0.20~0.22 | CVd=0.20~0.22 | CVd=0.20~0.22 |
| φ=10°~30° | φ=10°~30° | φ=10°~30° |
试验中发现,浆体速度逐渐减低,当形成滑动床时,进一步降低平均速度时,滑动床的移动变得不稳定。从不稳定滑动床移动,变动到固定床形式流动状态的速度范围大致为0.35m/s。
输送浓度在0.20~0.22范围变动时,通过图 6所示的调节管道倾角的装置使管道倾角逐渐增大时,倾角对滑动床高度的影响微乎其微。

|
| 图 6 调节管道倾角的装置 Fig.6 Device for regulating inclination angle of pipeline |
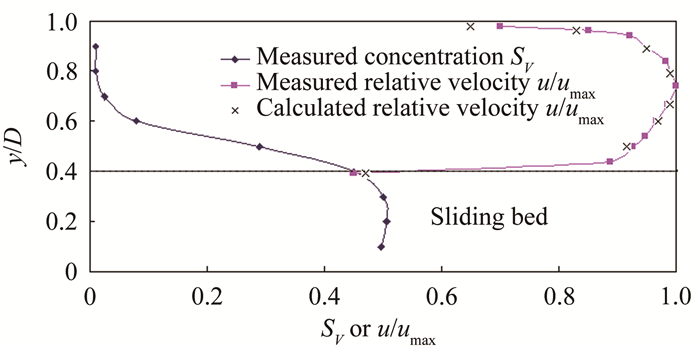
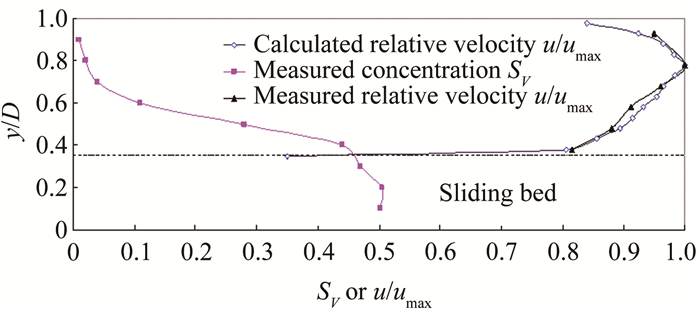
速度分布的计算和实测值如图 7和8所示,试验工况为表 1和2中第3组所列。
|
| 图 7 水平管道速度分布计算值和实测值对比 Fig.7 Comparison of calculated and measured values of velocity distribution in horizontal pipe |
|
| 图 8 倾斜管道速度分布计算值和实测值对比 Fig.8 Comparison of calculated and measured values of velocity distribution in inclined pipe |
计算发现,上层速度分布理论和实测度误差不超过10%,这说明前文中垂向剪应力呈线性分布的假设未导致过大误差,假设成立。
计算中发现,随着管道倾角的增大,零剪应力(即最大速度点)有向上偏移的趋势。这是由于在实验中,输送浓度不变条件情况下,上下层速度差U1-U2的增量大于速度U1的增量,导致界面剪切应力随着管道倾角增大而增大,从图 3可知,必然导致y1增大,进而零剪应力(即最大速度点)向上偏移。
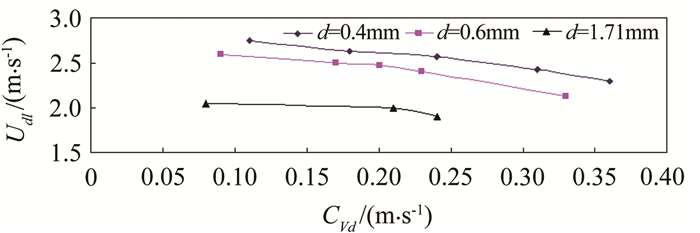
5.2 临界淤积速度计算模型的验证分析实验数据后发现,得到的淤积临界流速Udl随着颗粒平均粒径的d增大而减小,如图 9所示。同时,图 9中试验数据还表明,输送浓度CVd越大,则淤积临界流速Udl的值越小。
|
| 图 9 淤积临界流速与颗粒粒径和输送浓度的关系 Fig.9 Relationship between critical deposit velocity and particle transport concentration |
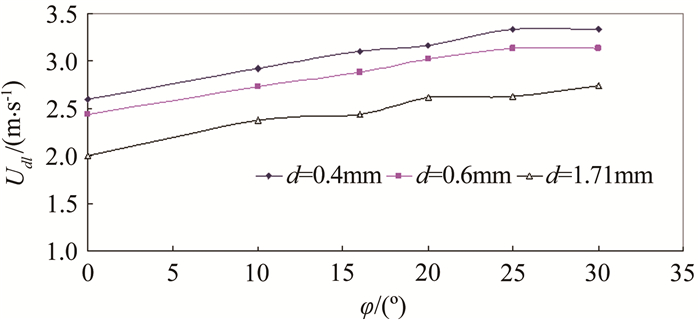
图 10显示了输送浓度CVd不发生较大波动(CVd=0.21~0.22)条件下,管道倾角对淤积临界流速Udl的影响。从图中可以看出,随着管道倾角的增大,3种级配颗粒的浆体淤积临界流速Udl的值也会相应增大。在管道角度超过25°以后,淤积临界流速增加的趋势有所减缓。
|
| 图 10 淤积临界流速和管道倾角关系 Fig.10 The relationship between the critical deposit velocity and the inclination of the pipeline |
试验中还发现,其他条件相同时,粗颗粒滑动床的速度比细颗粒滑动床快。这种现象可以从理论上进行解释。由于作用在滑动床床面的剪应力τ0(颗粒床滑动驱动力)与上下层界面阻力系数f12正相关(见式(9)),而f12与滑动床表面颗粒的粒径正相关(见式(9))。由于粗颗粒床面的颗粒较大,导致界面阻力系数f12较大,从而粗颗粒床面的剪应力τ0较细颗粒床面大,表现为粗颗粒滑动床具有较快的滑动速度。
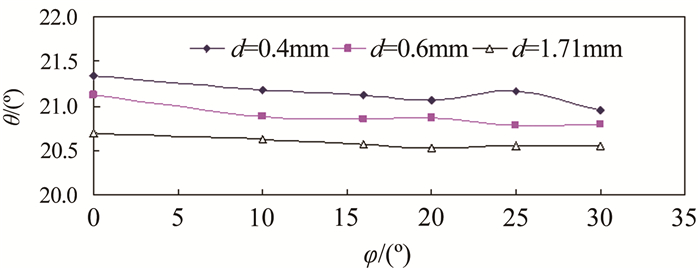
在维持输送浓度不变条件下,计算了临界淤积状态时滑动床角度θ的值,发现对于不同的管道倾角,其变化幅度为20.12°~21.40°。且颗粒越粗,则该角度越小。管道倾角越大,该值越小。
当输送浓度CVd不变时,滑动床角度随着管道倾角增大而呈现轻微减小趋势,如图 11所示。由此可以推断,管道倾角对于滑动床厚度的影响轻微。从而可以推断,从水平管道开始,随着管道倾角的增大,为了维持输送浓度不变,必须增大浆体速度Um,增大的Um主要用于平衡滑动床越来越大的重力下滑力分量,在此过程中,也稍稍减小了滑动床的厚度,如图 11所示。
|
| 图 11 管道倾角φ变化对滑动床角度θ的影响 Fig.11 The influence of the change of the pipe angle φ on angle of the sliding bed θ |
图 12为计算的淤积临界速度和实测的淤积临界速度的对比,计算值和实测值最大偏差为13%。可见,本文提出的淤积临界速度计算模型,用来预测颗粒粒径0.4、0.6和1.71mm的砂浆体淤积临界速度是较为可靠的。本文提出的方法对于其它条件下浆体淤积临界速度的预测,模型是否适用,还需要进一步检验。
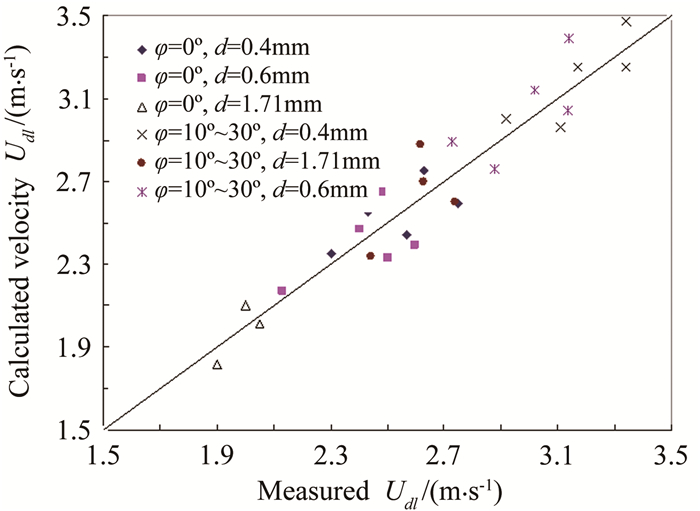
|
| 图 12 淤积临界流速Udl计算值和实测值对比 Fig.12 Comparison of calculated value and measured value of critical deposit velocityUdl |
(1)在水平管道扩散方程的基础上,提出了倾斜管道悬浮层颗粒浓度分布、滑动床厚的计算模型。
(2)通过分析滑动床受力平衡关系,给出了倾斜管道淤积临界速度的计算模型。
(3)通过垂向剪应力呈线性分布假设,给出了滑动床上方悬浮层速度分布模型。
(4)通过分析颗粒粒径为0.4、0.6和1.71mm,输送浓度在0.10~0.27的3种粗砂浆体在直径为150mm的试验管路中的流动试验数据,发现上层速度分布模型理论计算值和实测度误差不超过10%。淤积临界流速与平均粒径和输送浓度负相关。当输送浓度不变时,管道倾角对于滑动床厚度的影响甚微。淤积临界速度的实验值模型计算值的对比表明,最大偏差不超过13%。
| [1] | 张士林. 浆体管道淤积流速数值计算方法研究[J]. 水力采煤与管道运输 , 2011 (4) : 6–9. Zhang S L. Research on numerical calculation method of slurry pipeline deposition velocity[J]. Hydraulic Coal Mining & Pipeline Transportation , 2011 (4) : 6–9. |
| [2] | 郗夏楠, 孙西欢, 李永业, 等. 管道水力输送临界流速研究进展综述[J]. 山西水利 , 2012 (3) : 36–38. Xi X N, Sun X H, Li Y Y, et al. Review of research progress on critical flow velocity of pipeline hydraulic transport[J]. Shanxi Water Resources , 2012 (3) : 36–38. |
| [3] | 陈琴瑞, 李甲. 浆体管道输送临界流速经验公式适宜性分析[J]. 中国矿山工程 , 2015, 4 (6) : 73–75. Chen Q R, Li J. Suitability analysis of empirical formulas for critical velocity in slurry pipeline transportation[J]. China Mine Engineering , 2015, 4 (6) : 73–75. |
| [4] | 王新民, 李天正, 张钦礼. 基于GA-ELM浆体管道输送临界流速预测模型研究[J]. 中国安全生产科学技术 , 2015, 11 (8) : 101–105. Wang X M, Li T Z, Zhang Q L. Study on prediction model of critical flow velocity in slurry pipeline transportation based on GA-ELM[J]. Journal of Safety Science and Technology , 2015, 11 (8) : 101–105. |
| [5] | 秦德庆, 曹斌, 夏建新. 不同颗粒物料管道水力输送不淤临界流速的确定[J]. 矿冶工程 , 2014, 34 (1) : 9–11. Qin D Q, Cao B, Xia J X. Study on non-depositing velocity of different particle materials in pipeline by hydraulic transportation[J]. Mining and Metallurgical Engineering , 2014, 34 (1) : 9–11. |
| [6] | 旷水泉. 大石河铁尾矿高浓度管道输送临界流速研究[J]. 水力采煤与管道运输 , 2015 (2) : 1–5. Kuang S Q. Study on critical flow velocity of high concentration pipeline transportation of iron tailings in Dashihe[J]. Hydraulic Coal Mining & Pipeline Transportation , 2015 (2) : 1–5. |
| [7] | Souza P T C, Moraes J D, Slatter P T, et al. Modelling the critical velocity for heterogeneous flow of mineral slurries[J]. In International Journal of Multiphase Flow , 2014, 65 : 31–37. DOI:10.1016/j.ijmultiphaseflow.2014.05.013 |
| [8] | Sanni E S, Olawale S A, Adefila S S. Theoretical study of sand entrainment and deposits in horizontal oil transport[J]. Science Research , 2015, 3 (6) : 314–323. DOI:10.11648/j.sr.20150306.18 |
| [9] | Rice H P, Fairweather M, Peakall J, et al. Constraints on the functional form of the critical deposition velocity in solid-liquid pipe flow at low solid volume fractions[J]. Chemical Engineering , 2015 (126) : 759–770. |
| [10] | Boulanger J, Joan B. Sand suspension deposition in horizontal low-concentration slurry pipe flows[J]. Granular Matter , 2016, 18 (2) : 1–10. |
| [11] | Harbottle D, Fairweather M, Biggs S. The minimum transport velocity of colloidal silica suspensions[J]. Chemical Engineering Science , 2011, 66 (11) : 2309–2316. DOI:10.1016/j.ces.2011.02.012 |
| [12] | Rice H. Transport and deposition behaviour of model slurries in closed pipe flow[D]. Leeds:University of Leeds, 2013:112-122. |
| [13] | Kotzé M, Sutherland A, Kotzé R. A system to estimate coarse particle velocities at the pipe wall in settling slurry flow[J]. Flow Measurement and Instrumentation , 2013 (32) : 63–70. |
| [14] | Mario R R, Eduardo S A. Two-layer model for horizontal pipe flow of newtonian and non-newtonian settling dense slurries[J]. Ind Eng Chem Res , 2012, 51 (20) : 7095–7103. DOI:10.1021/ie201667k |
| [15] | Abd Al Aziz A I, Mohamed H I. A study of the factors affecting transporting solid-liquid suspension through pipelines[J]. Open Journal of Fluid Dynamics , 2013 (3) : 152–162. |
| [16] | Vaclav M, Jan K. Stationary-and sliding beds in pipe flows of settling slurry[C]//The Proceedings of the 15th International Freight Pipeline Society Symposium. Prague:Taylor & Francis, 2014:231-237. |
| [17] | Matouseka V, Krupickaa J, Penika V. Distribution of medium-to-coarse glass beads in slurry pipe flow:evaluation of measured concentration profiles[J]. Particulate Science and Technology , 2014, 32 (2) : 186–196. DOI:10.1080/02726351.2013.840706 |
| [18] | Matouseka V, Krupickaa J, Penika V. Distribution of medium-to-coarse glass beads in slurry pipe flow:evaluation of measured concentration profiles[J]. Particulate Science and Technology , 2014, 32 (2) : 186–196. DOI:10.1080/02726351.2013.840706 |
| [19] | Sape A M. An overview of theories describing head losses in slurry transport:a tribute to some of the early researchers[J]. Pipeline and Riser Technology , 2013, 4 (03) : 233–241. |
| [20] | 赵利安.大颗粒浆体管内流动规律研究[D].阜新:辽宁工程技术大学, 2011:98-109. Zhao Li-an. Study on flow law of large particle slurry in pipeline[D]. Fuxin:Liaoning Technical University, 2011:98-109. |
| [21] | 林雪松, 陈殿强, 何峰, 等. 固液两相流中颗粒浓度分布统一公式的研究[J]. 水资源与水工程学报 , 2013, 24 (4) : 82–84. Lin X S, Chen D Q, He F, et al. Study on unified formula of particle concentration distribution in two-phase flow of liquid-solid[J]. Journal of Water Resources & Water Engineering , 2013, 24 (4) : 82–84. |
| [22] | 傅旭东, 王光谦. 低浓度固液两相流中的粗颗粒浓度分布[J]. 清华大学学报(自然科学版) , 2002, 42 (10) : 1361–1364. Fu X D, Wang G Q. Concentration distribution of coarse particles in dilute solid/liquid two-phase floes[J]. Journal of Tsinghua University (Science & Technology) , 2002, 42 (10) : 1361–1364. |
| [23] | 赵利安, 孟庆华. 伴有滑动床的浆体倾斜管道摩阻损失研究[J]. 矿业研究与开发 , 2008, 28 (2) : 3–6. Zhao L A, Meng Q H. Research on friction loss of slurry with sliding bed in inclined pipeline[J]. Mining Research and Deve-lopment , 2008, 28 (2) : 3–6. |
| [24] | Shook C A, Roco M C. Slurry flow:principles and practice[M]. Oxford: Butterworth-Heinemann , 1991 : 123 -124. |
| [25] | 张士林, 许振良, 邵龙潭. 弓形断面管道的紊流速度分布[J]. 辽宁工程技术大学学报 , 2006, 25 (1) : 63–65. Zhang S L, Xu Z L, Shao L T. Water velocity in pipe of arching section[J]. Journal of Liaoning Technical University , 2006, 25 (1) : 63–65. |
| [26] | Hisham A N, Shook C A, Nabil E. Isokinetic probe sampling from slurry pipelines[J]. The Canadian Journal of Chemical Engineering , 1984, 62 (2) : 179–185. DOI:10.1002/cjce.v62:2 |
| [27] | 赵利安, 姜威. 粗颗粒高浓度流体管道流动浓度分布研究[J]. 泥沙研究 , 2016 (1) : 37–41. Zhao L A, Jiang W. Study on concentration distribution of pipe flow with high concentration coarse particles[J]. Journal of Sediment Research , 2016 (1) : 37–41. |



