FAE通过中心炸药的爆炸驱动将液体燃料抛撒到空气中,燃料破碎并雾化后与空气混合形成可燃云雾,对该云雾点火可形成云雾爆轰。影响FAE威力的关键因素是液体燃料的抛撒及雾化效果,而该效果在很大程度上决定于液体燃料的首次破碎。从首次破碎的形成机理出发,液体燃料首次破碎的发生是由液体环内、外侧界面的Richtmyer-Meshkov不稳定性(RMI)和Rayleigh-Taylor不稳定性(RTI)的共同作用所导致的。
半个世纪以来,国内外研究者就气液界面的RMI和RTI开展了不少研究工作。Samirant[1]等利用超高速摄影及X射线照相等测试技术获得了液体燃料爆炸抛撒的实验照片。Gardner[2-3]研究了液体燃料的爆炸抛撒过程,将抛撒过程分为近场的首次破碎阶段和远场的二次破碎和膨胀阶段,并就FAE燃料抛撒的近场提出了径向膨胀的薄膜线性不稳定模型。施红辉等[4-5]利用矩形激波管研究了气液界面上RMI后期流体混合区的混合现象。邹立勇、黄文斌等[6-7]在竖式激波管中研究了高压气体驱动液体的界面RTI问题。李磊、任晓冰等[8-9]通过阴影照相获得气液界面破碎形态变化的时间序列,利用平面激光诱导荧光(PLIF)得到了径向膨胀液体环内诱导的荧光照片。
上述实验或是在一维激波管内研究气液界面的RMI和RTI,没有关于液体环轴对称抛撒的实验结果;或是由于炸药的高温、高压及瞬态效应所带来的观测难度而没有针对液体环内侧界面的形成、不稳定性的发展直至发生首次破碎的实验照片。为此,本文采用垂直放置的矩形截面激波管结合梯形扩张段模拟液体轴对称抛撒,利用高速摄影技术系统研究液体轴对称抛撒过程中甘油/空气混合区界面不稳定性的发展过程。
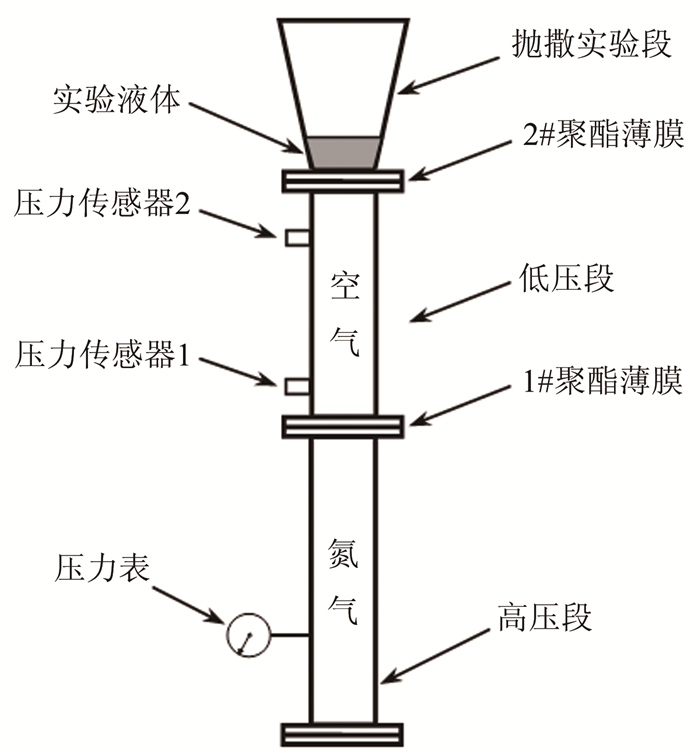
1 实验装置与方法图 1为实验装置示意图的正视图。装置垂直设置, 主要由3部分组成,位于底部的是长为800mm、截面形状为40mm×20mm的矩形、充满氮气的高压段;位于中部的是长为600mm、截面同样为40mm×20mm的矩形、内部为环境空气的低压段;位于上部的是试验段,其正面为梯形,底部宽40mm,高度为600mm,扩张角为15°,试验段的上部开口与环境大气相连。高压段和低压段均由不锈钢制成,试验段由于需要采用光学测量,所用材料为20mm厚的高韧性高透光度的聚酯板。
|
| 图 1 实验装置正视图 Fig.1 The front view of experimental facility |
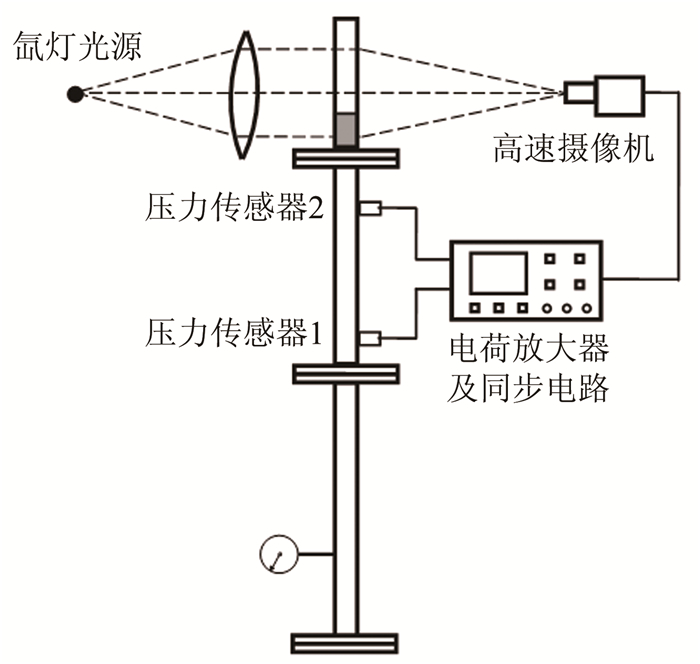
图 2为实验装置示意图的侧视图。氙灯光源通过透镜形成平行光束,垂直穿过液体抛撒实验段并通过Photron FastCam SA4高速摄影机记录流场图像。高速摄影机帧频为10 000帧/s,快门速度为1/95 000s,图像分辨率为512pixel×768pixel。
|
| 图 2 实验装置侧视图 Fig.2 The side view of experimental facility |
高压段和低压段之间由不同厚度的1#聚酯薄膜隔开,通过改变破膜压力获得不同马赫数的运动激波。试验段和低压段用厚度为0.01mm的2#聚酯薄膜隔开,并在2#聚酯薄膜的上方注入53.4mL的实验液体。实验液体如图 1和2中灰色部分所示,其正面为底部宽40mm、高度50mm的梯形,厚度为20mm。实验时在高压段充入高压氮气,1#聚酯薄膜在两侧压力差的作用下破膜并在低压段内形成运动激波,激波到达压力传感器1时,压力传感器产生一个电脉冲信号,此信号经电荷放大器增强后进入同步控制仪,经过适当延时后触发高速摄影机。激波继续向上运动,冲破2#聚酯薄膜后驱动实验液体形成液体的轴对称抛撒。
2 实验结果与分析 2.1 实验工况实验所用液体为甘油,20°常温下其密度ρ=1.26g/cm3、表面张力6.33×10-2N/m、粘性系数1.412Pa·s,实验时的Atwood数近似为1。采用了4种不同厚度的1#聚酯薄膜,获得不同马赫数的激波作用下的液体轴对称抛撒。本实验中激波管和试验段的截面均为矩形,初始扰动主要分布在不锈钢壁面和界面的中心,可近似认为是一个轴对称问题。
由于实验装置所限,实验过程中没有测量5区的压力p5。理论分析认为,5区压力在实验时间内首先为1个脉冲尖峰并导致2#膜片破裂,之后在气体中向下传播中心稀疏波,在液体中向上传播激波。考虑到甘油相对于气体的高密度、高粘性的特性,认为激波在气/液界面上反射所形成的5区压力近似等于固壁反射的压力,满足公式:
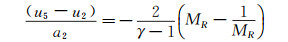 (1)
(1)
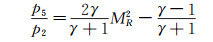 (2)
(2)
下标2和5分别表示激波管2区和5区的相关参数,MR为反射激波的马赫数。
此后,稀疏波尾及反射稀疏波头将导致5区压力逐渐降低。实际应用中的爆炸冲击波通常也是一个脉冲形的压力波,爆炸冲击波后中心稀疏波的作用同样使冲击波压力迅速衰减,往往还伴随着一个中心的负压区,这种情况通常通过冲击波前锋的运动马赫数和速度来量化研究。
具体实验参数如表 1所示:
| 参数 | 工况编号 | |||
| 1 | 2 | 3 | 4 | |
| 实验液体体积/mL | 53.4 | 53.4 | 53.4 | 53.4 |
| 1#聚酯薄膜厚度/mm | 0.05 | 0.075 | 0.125 | 0.15 |
| 2#聚酯薄膜厚度/mm | 0.01 | 0.01 | 0.01 | 0.01 |
| 破膜压力/MPa | 0.41 | 0.62 | 0.90 | 1.07 |
| 激波马赫数Ms | 1.35 | 1.46 | 1.57 | 1.63 |
| p5/MPa | 0.36 | 0.49 | 0.65 | 0.74 |
图 3是工况1所获得的高速摄影照片,从2#聚酯薄膜在激波作用下破膜并驱动实验液体开始加速运动到液体环发生破碎,总时间为8.0ms。由于不锈钢法兰对光线的遮挡,本实验无法获得初始界面上方约10mm范围内的光学图像,如图 3(a)下方所示。

|
| 图 3 工况1高速摄影照片 Fig.3 Photos of test condition 1 |
如图 3(b)所示,在后方激波的驱动下,实验液体向上加速运动,液体与自由空气的接触面由平面逐渐变为圆弧形。如图 3(c)所示,即实验时间为2.4ms时,实验液体与下方高压气体的界面进入透明观察窗。可以清晰地看到实验液体与下方高压气体的界面上沿横向随机分布着微小的扰动,尖钉和气泡分布在整个界面上,这是高压冲击作用下由RM不稳定性所形成的随机扰动。随着下方高压气体持续推动上方液体加速运动,由于是轻流体加速重流体,因此RT不稳定性逐渐增长,占据主导地位。甘油/空气混合区宽度逐渐增加,气泡和尖钉的高度也随之增加。由于不稳定性的发展,界面上会形成新的气泡和尖钉,如图 3(d)~(h)所示。
如图 3(i)所示,在甘油/空气混合区发展过程中,气泡的前缘基本保持圆形。而尖钉的发展由于受到周围的液体以及壁面的拖拽,尖钉的头部有雾化的迹象。图 3(j)为8.0ms时液体发生破碎的图像。可见实验液体的前端已经发生首次破碎,完整的液体块破碎成丝带状的液体碎片,而尖钉的顶部发生了强烈的雾化,即图 3(j)中部的黑色阴影部分。
2.3 不同驱动压力的实验结果比较图 4是4种不同工况下实验液体达到相同位置时的高速摄影照片。从图中可以看出,4种不同工况下的流场形状基本相同。随着1#聚酯薄膜厚度的增加,破膜压力升高,激波马赫数随之增大,高压驱动气体与实验液体的不稳定性界面上的扰动波数有逐渐增加的趋势。根据冲击模型[10],波数k=2π/λ,λ为扰动波的波长。可见,随着破膜压力的升高,在2#聚酯薄膜厚度相同的条件下,初始扰动波的波长λ随着激波马赫数的增大而减小。

|
| 图 4 4种工况抛撒过程照片 Fig.4 Photos of the dissemination process under four test conditions |
图 5是4种不同工况下实验液体发生首次破碎时的高速摄影照片。可以看出在不稳定发展的后期,随着液体向上运动,液体层的厚度越来越薄;最终,实验液体后方的高压气体冲破液体薄层,形成实验液体的首次破碎。比较图 5的4种工况,随着驱动压力的增加,尖钉端部的首次破碎范围越大,甘油/空气混合区的后方甚至已经出现了浓度较高的二次破碎所形成的雾化场(如图 5(c)和(d)箭头所指位置)。可见由于驱动压力的增加,尖钉的发展速度随之增大,其受到Kelvin-Helmholtz不稳定性和表面张力的影响更为强烈,尖钉发生破碎并与气流混合的程度也更为剧烈。文献[6]在分析一维激波管驱动Air-Water界面的RT不稳定性实验结果时指出,随着初始压力差的增加,气泡增长系数不断增加。本文的实验也表现出了类似的规律,但由于本文所研究的是二维问题,且涉及到RMI与RTI的耦合,故没有对气泡增长系数进行定量分析。

|
| 图 5 4种工况首次破碎照片 Fig.5 Photos of the primary breakup under four test conditions |
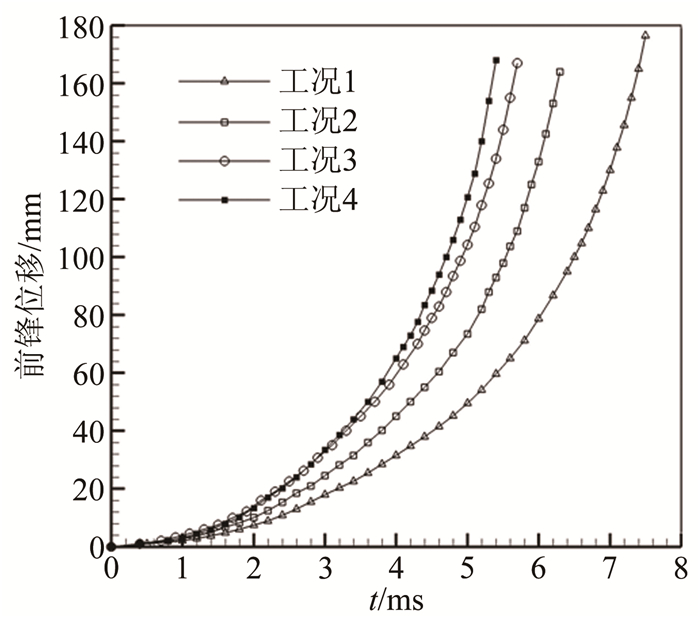
图 6是4种工况下实验液体前锋位移随时间的变化曲线。各时刻液体前锋的位移数值通过读取实验照片获得,液体前锋的初始位置为破膜前实验液体的上表面,曲线的结束时间为液体前锋开始发生首次破碎的时刻。从曲线图上可以看出,在本文的4种实验工况下,随着破膜压力的增大、激波的增强,实验液体的首次破碎位置基本保持不变,所对应的前锋位移均约为170mm。
|
| 图 6 液体前锋位移与时间的关系 Fig.6 Relationship between displacement of liquid front and t |
对实验液体前锋的位移时间曲线通过中心差分求解速度时间曲线,再对速度时间曲线通过中心差分求解加速度时间曲线,时间步长为等步长,均为0.4ms。由于液体加速运动初始阶段的液体前锋位移非常小,而通过照片直接读取的方式所获得的位移精度有限,通过数值差分计算出的速度和加速度的离散性较大,因此速度和加速度的离散点约从1ms开始选取。0ms所对应的初始速度显然为0,而0ms所对应的初始加速度则通过牛顿第二定理计算得出其近似解。利用甘油/空气界面反射激波的压力p5乘以初始实验液体的底部面积A1获得向上的推力F1,利用环境大气压力p0乘以初始实验液体的顶部面积A2获得向下的压力F2。由于重力与F1和F2相比均为小量,因此忽略重力的影响,用F1和F2两力之差除以实验液体的质量ml获得实验液体的初始加速度a0,即:
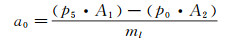 (3)
(3)
(其中A1=8.0cm2,A2=13.36cm2,ml=0.063kg)
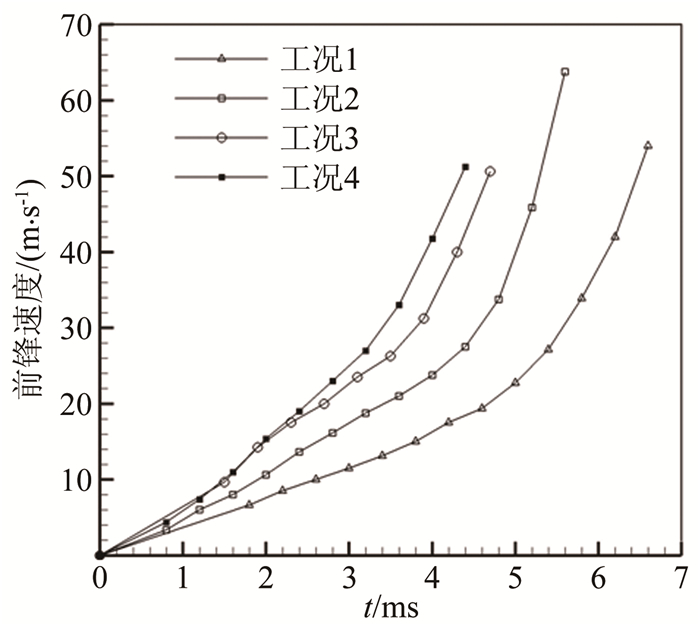
可得实验液体前锋的速度和加速度随时间的变化曲线如图 7和8所示:
|
| 图 7 液体前锋速度与时间的关系 Fig.7 Relationship between velocity of liquid front and t |
|
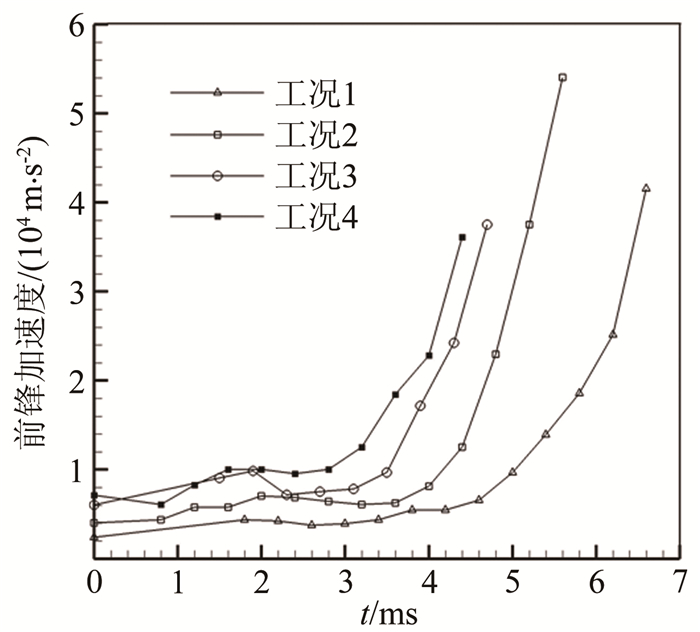
| 图 8 液体前锋加速度与时间的关系 Fig.8 Relationship between acceleration of liquid front and t |
从加速度曲线可以看出,在不同强度的激波驱动下,4条曲线的变化趋势基本相同。在3ms之前的时间范围内,各工况下的液体前锋加速度大小基本不随时间而改变,加速度曲线基本保持水平,在大约2~3ms的时间段略有下降,随后加速度随时间迅速增大。分析认为该现象出现的原因主要是破膜初期实验液体的位移较小,液体前锋的速度较低,因此实验液体的形状和厚度变化较小,即高压气体与实验液体的界面上单位面积所驱动的液体体积基本不变。在大约2~3ms的时间范围,由于1#聚酯薄膜破膜形成的稀疏波到达气液界面会导致驱动压力的下降,因此在该时间段,液体前锋的加速度略有降低。而抛撒后期,随着液体前锋迅速前行,实验液体的厚度迅速减小,单位面积的气液界面所对应的液体质量随之迅速减小。而在液体发生首次破碎之前,整个激波管与环境大气没有连通,驱动液体加速前行的高压气体的压力变化较小,因此抛撒后期的液体前锋加速度迅速增加。
3 结论利用垂直激波管装置并加以改造,采用高速摄影技术对甘油在激波驱动下的轴对称抛撒开展了一系列的实验研究。主要结论如下:
(1)通过透明的抛撒试验段可以获得液体轴对称抛撒过程中RT不稳定性和RM不稳定性的发展过程,获得混合区的气泡和尖钉生长直至液体发生首次破碎的实验照片。
(2)随着驱动压力的升高和激波马赫数的增大,初始扰动波的波长随之减小,不稳定性界面上的扰动波数随之增加。随着驱动压力的增加,尖钉的发展速度随之增大,其受到Kelvin-Helmholtz不稳定性和表面张力的影响更为强烈,尖钉发生破碎并与气流混合的程度更为剧烈。
(3)实验液体发生首次破碎的位置基本不随驱动压力的升高而改变。液体前锋的加速度曲线呈现出前期基本不变,后期迅速增大的趋势。
| [1] | Samirant M, Smeets G, Baras C, et al. Dynamic measurements in combustible and detonable aerosols[J]. Propellants Explosives Pyrotechnics , 1989, 14 : 47–56. DOI:10.1002/(ISSN)1521-4087 |
| [2] | Gardner D R. Near-field dispersal modeling for liquid Fuel-Air-Explosive[R]. Sandia National Laboratories Report, SAND-90-0686, 1990. |
| [3] | Gardner D R, Glass M W. A coupled near-field, far-field dispersal model for Fuel-Air-Explosives[R]. Sandia National Laboratories Report, SAND-90-0687, 1991. |
| [4] | 施红辉, 岸本熏实. 瞬态加速液柱的流体力学问题研究[J]. 爆炸与冲击 , 2003, 23 (5) : 391–397. Shi H H, Kishimoto M. Fluid mechanics in the transient acceleration of a liquid column[J]. Explosion and Shock Waves , 2003, 23 (5) : 391–397. |
| [5] | 施红辉, 卓启威. Richtmyer-Meshkov不稳定性流体混合区发展的实验研究[J]. 力学学报 , 2007, 39 (3) : 417–421. Shi H H, Zhuo Q W. Evolution of the fluid mixing zone in richtmyer-meshkov instability at a gas/liquid interface[J]. Chinese Journal of Theoretical and Applied Mechanics , 2007, 39 (3) : 417–421. |
| [6] | 邹立勇, 王建, 刘金宏, 等. 高压气体膨胀驱动Air-Water界面Rayleigh-Taylor不稳定性实验研究[J]. 高能量密度物理 , 2008, 2 : 49–53. |
| [7] | 黄文斌, 邹立勇, 刘金宏, 等. 初始扰动对于气液界面Rayleigh-Taylor不稳定性发展的影响[J]. 实验流体力学 , 2010, 24 (3) : 39–41. Huang W B, Zou L Y, Liu J H, et al. Effects of initial perturbations on Rayleigh-Taylor instability growth at gas-liquid interface[J]. Journal of Experiments in Fluid Mechanics , 2010, 24 (3) : 39–41. |
| [8] | 李磊, 崔箭, 董玉才, 等. 液体爆炸分散过程中界面破碎的实验研究[J]. 科学通报 , 2009, 54 (12) : 1693–1700. Li L, Cui J, Dong Y C, et al. Experimental investigations to the interfaces breakup during liquid explosive disseminations process[J]. Chinese SciBull , 2009, 54 (12) : 1693–1700. |
| [9] | 任晓冰, 李磊, 严晓芳, 等. 液体的爆炸抛撒特征[J]. 爆炸与冲击 , 2010, 30 (5) : 487–492. Ren X B, Li L, Yan X F, et al. Dispersion characters of liquid induced by explosion[J]. Explosion and Shock Waves , 2010, 30 (5) : 487–492. |
| [10] | Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Commun Pure App Math , 1960, 13 : 297–319. DOI:10.1002/(ISSN)1097-0312 |



