2. 上海市力学在能源工程中的应用重点实验室, 上海 200072
2. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China
大型鸟类(如鹰、隼)在空中飞翔时将翼尖初级飞羽(Primary feathers)分散开起到控制翼尖涡、减小诱导阻力的作用,同时鸟翼的等效面积增大,如图 1(a)所示,使升力得到提高。Newman[1]对黑秃鹰的高空翱翔和低空滑翔状态进行了研究,发现由于滑翔与翱翔时鸟翼和初级飞羽姿态不同,鸟所受到的阻力也不同。在高空翱翔时,鸟翼上的羽毛充分展开,增加鸟翼面积,减小下降速度,但翼面积的增加会提高鸟翼的型阻。在低空滑翔时,初级飞羽分散开并向下弯曲,其他羽毛收缩,鸟翼面积相对翱翔时较小,气流从初级飞羽之间穿过,此时鸟翼所受阻力较低,滑翔距离相对较远。Tucker[2-4]对哈里斯鹰、印度猎隼和黑秃鹫的翼尖初级飞羽进行了详细的研究。研究发现,不同鸟类初级飞羽的形状及其在飞行时的姿态有所差别,但是所起到的作用是一样的。初级飞羽不仅可以提高升力,减小阻力,还可以控制鸟类滑翔时的俯仰平衡;剪掉初级飞羽的鸟类的阻力比未剪的高出42%,该研究证实了初级飞羽减阻的重要作用。而将哈里斯鹰的初级飞羽插在机翼翼尖,而后在风洞中进行的测力实验表明[5],当主翼迎角从4°变化到14°时,升阻比相对于原型翼增加了107%,阻力降低了12%。受鸟翼结构的启发,Spillman[6-7]将多个小升力面安装在机翼翼尖来模拟初级飞羽(见图 1(b)),称之为翼尖帆片。随后进行了一系列风洞实验和飞行实验,以考察帆片的增升减阻效能。风洞实验结果表明,单片翼尖帆片可以降低12%的诱导阻力,3片翼尖帆片则可降低28%的诱导阻力,而帆片数达到5或6片时,平均单片帆片的减阻效率下降。因此,Spillman认为3或4片翼尖帆片的减阻效果最佳。飞行测试结果显示单帆片可以降低9%的诱导阻力,3片帆片降低29%的诱导阻力,与风洞实验的结果一致;而飞机的最大升阻比从12.5提高到15.8,增长幅度超过25%。

|
| 图 1 翼尖帆片和鸟类飞行中张开的初级飞羽 Fig.1 Wing tip sails and the separation of primary feathers of birds |
陈明岩和齐孟卜[8-9]用数值模拟和实验的方法对翼尖帆片的安装参数进行了优化设计。Smith[10]对帆片的安装角、扭转角以及上下反角对机翼气动特性和翼尖涡涡量分布的影响进行了研究,负安装角和扭转角均可以改变帆片的局部升力方向,抵消部分阻力,提高机翼升阻比;相比于相同等效面积的主翼,帆片翼能够产生更多的升力;帆片上、下反角可以改变翼尖涡涡量分布,使翼尖涡远离尾流区,减缓机翼后缘的下洗运动。Miklosovic[11]、Catalano[12-13]均对翼尖帆片的上、下反角与气动特性的关系进行了实验研究,并给出各自的优化结果。经优化后的上、下反角的大小虽然有所差异,但各帆片间上、下反角之差均与陈明岩和齐孟卜[8-9]的优化结果一致,前后帆片倾角之差均为15°时,主翼的气动特性改善效果最佳,翼尖涡涡量削弱程度最明显。Srikanth[14]对与翼尖帆片结构类似的组合翼尖小翼的研究发现,组合翼尖小翼可以明显减缓机翼上翼面的流动分离。徐胜金和杨可等[15]用PIV技术对组合小翼的翼尖涡结构进行了实验研究,并提出组合小翼与翼梢喷流联合控制翼尖涡的方法[16]。研究结果表明,组合小翼上较强的涡都是由正上反角小翼产生的,这在削弱翼尖涡强度中起到关键的作用,组合小翼最大涡量降低到原型翼的13.7%[15];组合小翼“+0-”构型可以提高机翼的升力,最大升力系数提高12.3%,而“-0+”构型的升力系数与原型机翼基本相同[16]。对组合小翼和喷流联合控制的研究发现,喷流可以控制翼尖涡涡核位置,对翼尖涡的产生和发展有一定的抑制作用。“+0-”组合小翼与“向下喷流”联合对翼尖涡控制效果较好,在距机翼后缘三倍弦长的尾流截面上,瞬态涡量峰值的平均值相比单独用“+0-”构型控制时减小37%,比原型翼减小79%,该方法削弱翼尖涡涡量的效果较好。
与鸟类在高空中飞翔不同,鹈鹕等水鸟在近水面可长距离滑翔,如图 1(c)所示,初级飞羽与地面效应同时起到流动控制和减少能耗的作用。有学者对近水面鸟类滑翔进行了野外的观察研究。Withers[16]用摄影的方法记录黑撇水鸟在近水面滑翔的姿态。研究结果表明,地面效应对减少鸟类在近水面滑翔时的阻力起到了重要的作用,可降低滑翔迎角和下降速度,减小飞行中的能量消耗。Hainsworth[17]用摄影的方法研究了褐鹈鹕在地效区内、外编队飞行时的飞行高度、相邻鸟的翼尖间距和纵向位移变化规律。发现地面效应减小了鹈鹕滑翔角和下降速度,延长滑翔时间,减小滑翔时所受的阻力。褐鹈鹕在滑翔时高度最大变化范围为24~45cm,减小诱导阻力范围为41%~58%。Hainsworth认为,与自由空间可预知的流场相比,地面效应区内尾涡和水(地)面的相互作用产生复杂、不可预知的流场可以改善减阻效果。Withers和Hainsworth的研究结果表明,地面效应对鸟类在近水面滑翔的气动特性有非常重要的影响。
翼尖初级飞羽和地面效应是影响鹈鹕等水鸟在近水(地)面滑翔时流动控制效率的重要因素。虽然有众多学者对初级飞羽和地面效应分别进行了深入的研究,但是至今尚无初级飞羽对地面效应下鸟翼气动特性影响的研究报道,而野外观测的数据完整性和系统性不足。因此,本研究在实验室中采用不同形状的翼尖帆片模拟鸟类的初级飞羽,测量和比较在地面效应下它们对机翼气动力造成的差异,进而通过分析不同类型帆片对翼尖涡产生的影响,从流动结构的角度探究气动力产生差异的原因。
1 实验设置实验在上海大学力学所小型回流式风洞中进行,开口实验段截面为400mm×400mm,湍流度为0.1%。机翼模型采用三帆片布局,分别将梯形帆片和椭圆帆片安装于主翼翼尖,如图 2和3所示。主翼为弦长C=130mm、半翼展L=195mm的NACA4412矩形机翼;在自由空间中,采用小展弦比机翼将带来翼尖涡强度增加,诱导阻力随之增长的问题。但文献[21]研究了展弦比对地效翼升力影响,比较了展弦比λ=0.5~5共7个矩形机翼的升力-迎角曲线,发现λ=2~3时, 随间隙h的减小, 升力系数的增长最大。参考上述文献的结果,并考虑到地面效应对下洗运动的抑制作用,本实验选取机翼展弦比λ=3。2种帆片均采用NACA23012翼型,翼根与翼梢的相对扭转角为12°;梯形帆片几何尺寸参考江永泉[19]的优化结果,展长为32.5mm,即24%C,根弦长20mm,梢弦长10mm;椭圆帆片的展长为32.5mm,翼根弦长为20mm,即长轴为65mm、短轴为20mm的半椭圆;帆片安装参数参考陈明岩和齐孟卜[8-9]的优化结果,上反角分别为15°,0°和-15°,安装角分别为-18°,-15°和-12°。翼尖帆片的安装位置处于主翼弦长的35%至87%之间。

|
| 图 2 梯形翼尖帆片机翼 Fig.2 Trapezoidal wing tip sails |

|
| 图 3 椭圆翼尖帆片机翼 Fig.3 Elliptical wing tip sails |
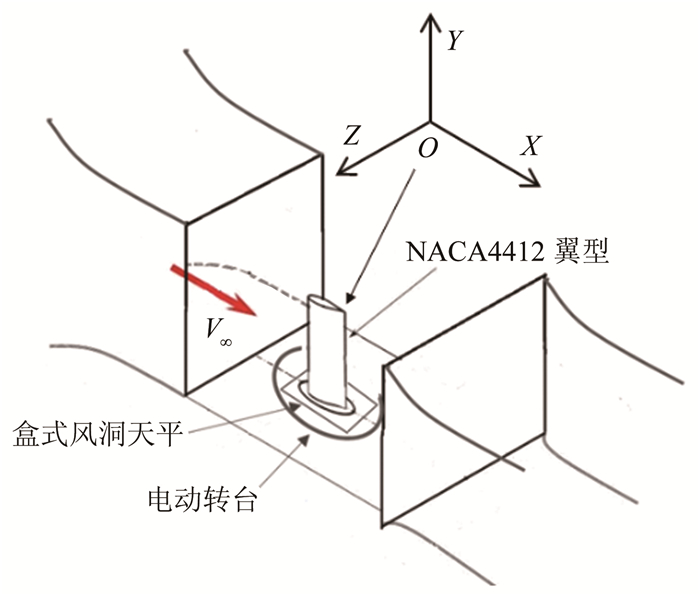
实验风速为17.5m/s,基于主翼弦长的雷诺数为1.5×105。实验布置和坐标系如图 4所示,自由来流方向为X轴正方向,竖直方向为Y轴正方向,Z轴与X-Y平面遵循右手定则,坐标系原点为机翼翼尖后缘点。机翼下翼面附近布置有前缘30°劈尖的有机玻璃光滑平板模拟地面,与X-Y平面平行。平板前缘与机翼迎角0°时的前缘在X方向的距离为150mm。经测量,机翼前后缘范围内平板边界层厚度大致为1.5mm,而实验最小间隙比0.1条件下,后缘与平板表面的间隔为13mm,比边界层厚度大一个数量级,因此忽略了边界层的影响。机翼的一端垂直固定在六分量盒式天平上,将七孔探针水平安装于机翼下游平行于X轴,用以扫描下游X=0.25C处Y-Z截面的速度分布。扫描截面面积为130mm×130mm,在小间隙比时适当减小机翼后缘下方的测量区域,防止探针与地板碰撞,探针测量步长为3.25mm,水平和竖直方向各41个测点,共41×41=1681个测点。通过七孔探针扫描所获得的数据为速度分布,本文所讨论的翼尖涡涡量则根据涡量的定义从速度场中导出。
|
| 图 4 实验段布局示意 Fig.4 Sketch of the experimental setup |
在机翼下表面附近布置光滑平板模拟地面,通过步进位移控制系统调整机翼后缘与地板之间的距离。定义间隙比h*=h/C,其中h为机翼后缘与地板的间距。
实验中主翼迎角α范围为-4°~25°,间隙比h*有0.1、0.15、0.3、0.5和1.0等5种工况,每个工况的升、阻力经多次测量,数据重复性良好,气动力实验结果均为5次测量的平均值。
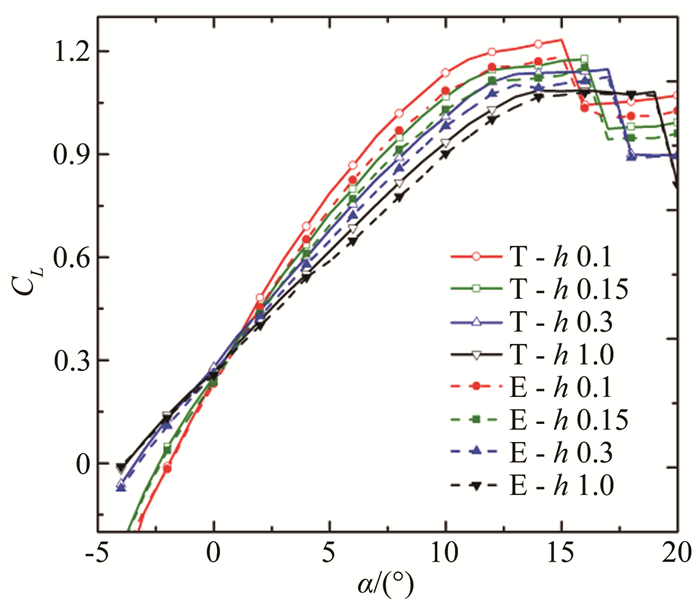
2 实验结果讨论 2.1 升力和阻力图 5是2种机翼在不同间隙比下升力系数CL随主翼迎角变化的曲线,图中字母T表示梯形帆片(Trapezoidal tip sails),E表示椭圆形帆片(Elliptical tip sails)(下同)。在迎角α0=-0.5°~1.0°范围内时,尽管2机翼升力线随间隙比的减小而无明显变化,但升力线斜率变化显著,此时各条升力线相互交汇。说明该迎角范围内,不同形状的翼尖帆片机翼具有相同的升力。在地面效应中普遍存在升力线在某迎角α0附近相交的现象,但由于不同翼型下翼面与地面形成的流道形状不同,造成迎角α0的值有所区别,如NACA23012机翼的α0约为3°~4°[22]。在迎角α < α0时,升力系数随着间隙比的下降而减小,而零升力迎角随之增大。主要是由于下翼面的曲面与地面之间形成收缩-扩张通道产生文丘里效应,使下翼面气流流速增大,静压减小,从而形成负升力。间隙比越小,文丘里效应越明显。当迎角α>α0时,随着间隙比的减小,2种机翼升力线的斜率和最大升力系数均有不同程度的提高。从间隙比1.0减小到0.15时,椭圆帆片和梯形帆片机翼的最大升力系数分别增大9.7%和13.5%,梯形帆片的增升效率高于椭圆帆片。但两机翼失速迎角均从19°降低到15°。机翼升力系数随间隙比的下降而增大主要有2部分原因:(1)机翼下翼面与地面之间形成收缩通道,在受到阻塞作用时流量下降,使静压提高,一部分流体从下翼面绕过机翼前缘,上翼面流速加快,从而静压减小;上下翼面的压差增大,使机翼获得额外升力,并且间隙比越小,升力系数提高越显著。(2)机翼不断靠近地面,翼尖涡受到抑制,减小了下洗角,从而在相同的几何迎角下,间隙比越小,机翼有效迎角越大,机翼升力系数随着间隙比的减小而增大。因此,尽管机翼失速的几何迎角随着间隙比的减小而下降,实际上对应的有效失速迎角应基本相同。
|
| 图 5 升力系数随迎角变化曲线图 Fig.5 Variation of the lift coefficient CL with angles of attack α |
在相同间隙比下,当机翼迎角α≤α0时,2种帆片机翼的升力系数较为接近,椭圆帆片机翼的升力稍低于梯形帆片机翼;当机翼迎角α>α0时,梯形帆片的升力线斜率和最大升力系数均高于椭圆帆片,2种帆片机翼的失速迎角保持不变。在间隙比h*=1.0、0.3和0.15时,梯形帆片的最大升力系数分别比椭圆帆片高0.6%、1.9%和2.17%,即随着间隙比的下降,梯形帆片和椭圆帆片翼的最大升力系数之差不断扩大。梯形帆片的增升效率随着间隙比的减小而逐步优于椭圆帆片。对于相同间隙比,2种帆片翼升力系数的差距也随着迎角的增加而不断扩大。
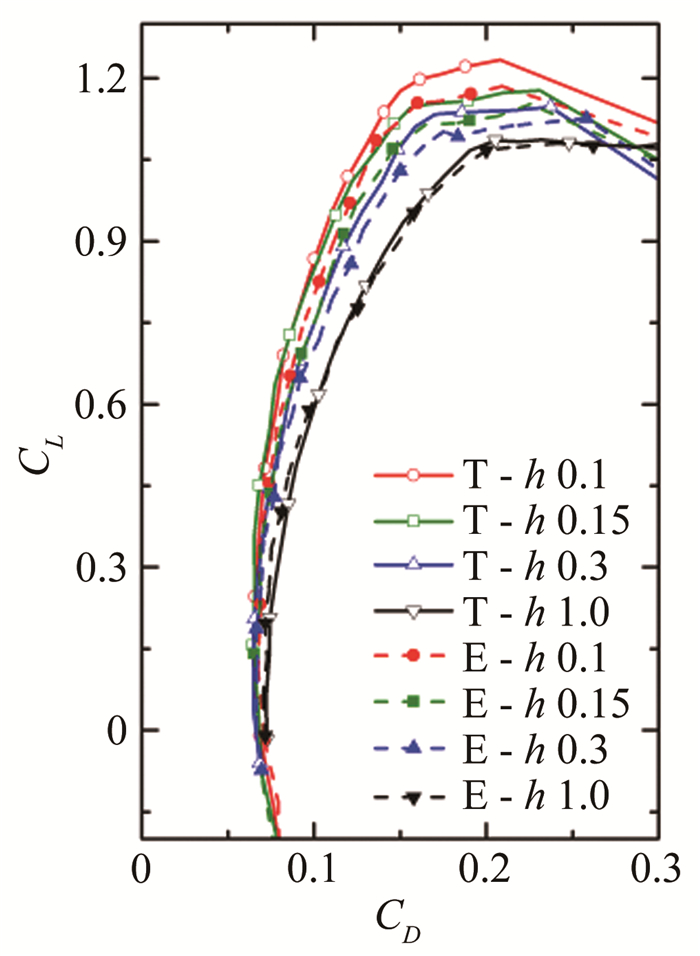
图 6是2种机翼在不同间隙比下的极曲线图。在升力增加的阶段,对应于相同的升力系数,机翼越靠近地面则受到阻力则越小。在间隙比h*=1.0时,2种帆片机翼的曲线几乎重合,表明机翼在受到相同升力的同时,所承受的阻力也基本相同。然而当间隙比减小,2种帆片阻力的差距在相同升力时逐渐扩大,梯形帆片机翼的阻力系数低于椭圆帆片机翼。
|
| 图 6 升力系数随阻力系数变化曲线 Fig.6 Variation of the lift coefficient versus drag coefficient |
机翼的总阻力主要由零升阻力和诱导阻力组成,其中诱导阻力系数为[23]:
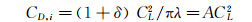
式中:A是诱导阻力因子,δ是机翼形状相对于椭圆机翼的修正值,λ是机翼的展弦比。
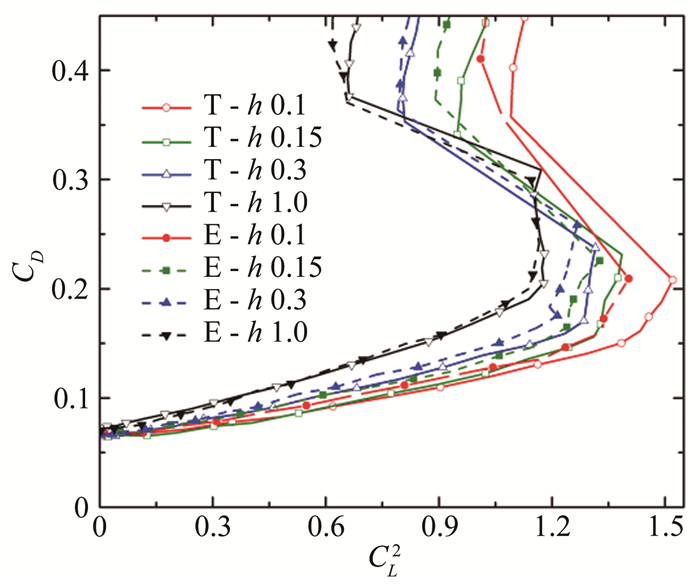
对比图 7中2种机翼的阻力系数随CL2的变化曲线,在机翼失速之前,曲线随升力系数的平方线性增长的部分即为诱导阻力CD, i,曲线与纵轴的交点即为零升阻力,实验数据与理论公式吻合良好。图中线性段斜率由诱导阻力因子A=(1+δ)/πλ决定,曲线斜率越小表明机翼在产生相同升力时具有较小的诱导阻力。表 1列出在线性段各个间隙比时2种机翼诱导阻力系数斜率的差异。随着间隙比的减小,下洗运动受到地面抑制,机翼的诱导阻力系数均逐渐减小。间隙比h*=1.0时,2机翼的诱导阻力无明显差别,随着间隙比的减小,同等升力下,椭圆帆片机翼的诱导阻力系数均超过梯形帆片机翼,并且间隙比越小,2机翼诱导阻力系数的差距越大,即随着间隙比的减小,梯形帆片减小诱导阻力的效率逐渐高于椭圆帆片。此外,研究表明[6],曲线中线性段末端向上折起的位置即为帆片表面发生流动分离后引起的阻力快速增长,因此,从图中可以判断出各工况下帆片表面流动分离所对应的迎角,例如椭圆帆片翼该点对应的迎角为12°。
|
| 图 7 阻力系数随升力系数的平方变化曲线图 Fig.7 Variation of the drag coefficient CD with CL2 |
| (1+δ)/πλ | h*=0.15 | h*=0.3 | h*=1.0 |
| 梯形帆片 | 0.069 | 0.082 | 0.113 |
| 椭圆帆片 | 0.080 | 0.089 | 0.114 |
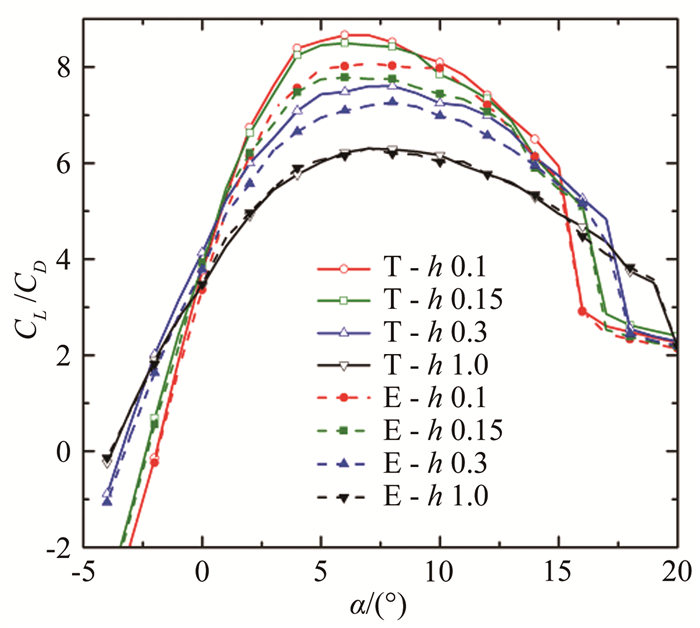
图 8为2种机翼在不同间隙比下升阻比随主翼迎角变化的规律。同一种机翼的升阻比随间隙比的减小均有不同程度的提高。间隙比从h*=1.0减小到0.15时,梯形帆片翼和椭圆帆片翼的最大升阻比分别提高34.7%和23.3%,地面效应对梯形帆片翼升阻比的增加有更为显著的影响。在间隙比h*=1.0时,梯形帆片与椭圆帆片的升阻比曲线几乎重合,2种帆片此时对机翼气动特性有相同的影响效果。而当间隙比减小至h*=0.3时,梯形帆片的升阻比明显高于椭圆帆片,最大升阻比相差4.7%;间隙比降至h*=0.1时,梯形帆片与椭圆帆片之间的升阻比差距进一步扩大,最大升阻比差距高达9.1%。
|
| 图 8 升阻比随迎角变化曲线 Fig.8 Variation of the lift-drag ratio with angles of attack α |
|
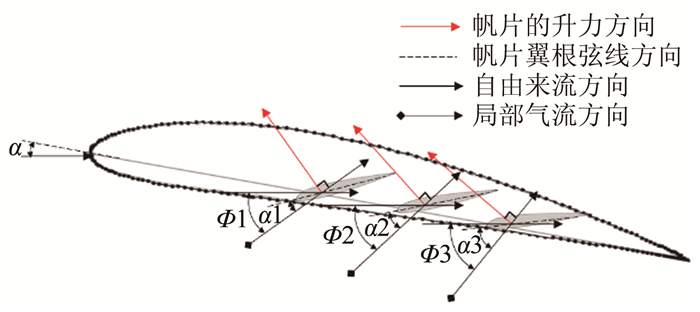
| 图 9 翼尖帆片局部气流及升力方向示意图 Fig.9 Schematic diagram of local flow direction at the wing tip sails |
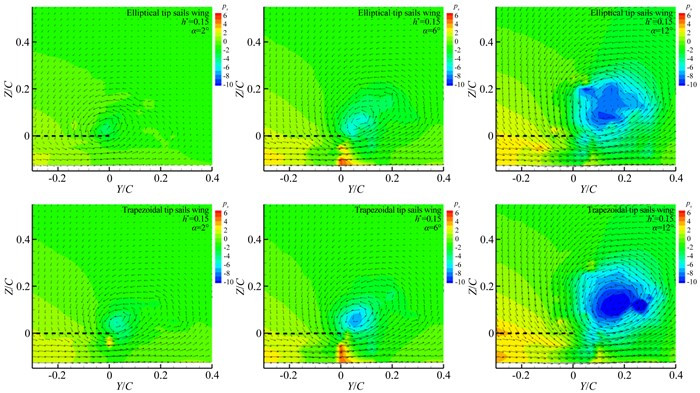
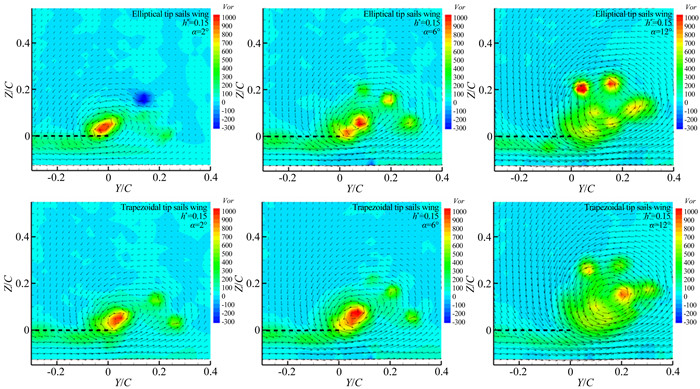
图 10和11分别对比了机翼迎角α=2°、6°和12°,间隙比h*=0.15时,梯形和椭圆帆片机翼翼尖涡速度场、静压分布和涡量分布,图中黑色虚线表示机翼后缘在速度场平面上的投影位置。基本流动形态为主翼的翼尖集中涡被帆片翼尖生成的3个小尺度涡旋所环绕并互相诱导,涡旋各自的强度受迎角、间隙比、帆片形状等因素的影响而有所不同。尽管本实验采用的梯形和椭圆形帆片具有相同的展长和根弦长,但较大的迎风面积使梯形帆片对气流产生较高的阻塞率,并在上下翼面形成更高的压力差。因此,如图 10所示,在各相同迎角,梯形帆片机翼的静压均低于椭圆帆片机翼,表明其翼尖涡旋转角速度更大,涡旋较为集中。随着迎角的增加,2种机翼的翼尖涡的静压逐渐降低,翼尖涡增强。但由此尚不能判断涡旋的强弱差异,而应当由涡通量(或环量)进行判别,以分析翼尖涡强度改变对诱导阻力的影响。因此,在图 11中给出各工况的涡量分布并由此积分导出涡通量(见表 2),比较和讨论2种帆片机翼升/阻力改变的原因。
|
| 图 10 2种机翼翼尖涡静压分布随迎角变化过程及比较(α=2°、6°和12°,间隙比h*=0.15) Fig.10 Comparison of the static pressure distributions of tip vortices for two wings at different angles of attack |
|
| 图 11 2种机翼翼尖涡涡量分布随迎角变化过程及比较(α=2°、6°和12°,间隙比h*=0.15) Fig.11 Comparison of the vorticity distributions of tip vortices for two wings at different angles of attack |
| 涡通量/(ω·S) | α=2° | α=6° | α=12° |
| 椭圆形帆片 | 8.26 | 15.83 | 32.12 |
| 梯形帆片 | 9.93 | 15.38 | 30.44 |
由于翼尖涡为螺旋状流动,对于给定自由来流迎角α,机翼翼尖外侧局部气流的方向角Φ与α的比值Φ/α随着离开翼尖的距离增加而迅速下降,而离翼尖相同间距情况下,从翼尖前缘至后缘的方向角Φ呈线性增长趋势[6, 9, 19],如图 9所示。因此,各帆片的有效迎角由局部方向角Φ以及帆片安装角、扭转角决定,此时各帆片有效迎角的差异导致在其梢部也生成不同强度和旋转方向的小尺度翼尖涡,如图 11所示。例如在主翼迎角α=2°时,3个帆片的根弦至梢弦几何迎角展向变化范围为分别为-16°~-4°、-13°~-1°和-10°~0°。从图中涡量分布推断,对于椭圆形帆片翼,由于前帆片的几何迎角沿展向均为较大的负值(-16°~-4°),且局部气流方向角Φ1较小,因此有效迎角也为负值,使得帆片上翼面压力高于下翼面,气流绕过帆片梢部形成从上翼面至下翼面逆向旋转的涡,涡量为负值,造成负升力,抵消了主翼的部分升力;而对于中帆片,几何迎角有所减小(-13°~-1°),局部方向角Φ2增大,其结果是有效迎角增加,并使帆片上下翼面压力平衡,无明显翼尖涡生成,对升力的贡献不明显;后帆片安装位置更加靠近主翼后缘,局部方向角Φ3进一步增大,同时几何迎角为最小(-10°~0°),实际气流迎角增长为正值,所生成的小尺度涡对应于涡量分布云图中右下方较弱的正涡量,对机翼额外提供正的升力。在主翼迎角增加至α=6°,主翼集中的翼尖涡被帆片分散成2个涡量较弱的小涡,涡量明显降低。同时,由于各帆片的有效迎角也随着局部方向角的增大而增大,不再具有负迎角,从而获得正的帆片升力。主翼迎角进一步增加到α=12°时,前帆片梢部有效迎角已超过临界迎角,形成翼尖失速,无法对主翼提供额外升力,可观察到前帆片翼尖有强烈涡量集中。中、后帆片处于前帆片的下洗尾流中,有效迎角反而小于前帆片,翼尖涡量依次减弱。以往的研究表明[6],前帆片对机翼增升减阻的效果最为重要,后帆片次之,中帆片作用最弱,3个帆片通过将翼尖涡“梳理”为匀直气流而起到增升减阻的效果。
对于梯形帆片,在小迎角α=2°时,从涡通量表 2中可以看出其翼尖涡强度大于椭圆帆片,翼尖外侧的局部气流方向角更大,各帆片有效迎角也大于相应位置处椭圆帆片的迎角。从涡量云图中观察到除前帆片翼尖涡涡量较为微弱外,中、后帆片的正涡量大于相应的椭圆帆片的涡量,表明帆片处于正迎角,并为机翼带来附加的升力贡献,但此时诱导阻力大于椭圆帆片的诱导阻力。随着迎角提高到α=6°,主翼翼尖涡仍保持为一个集中涡,且旋转角速度(涡量的1/2)大于椭圆帆片,这是与椭圆帆片流场结构的主要区别。然而其涡通量即涡旋强度略低于椭圆帆片,表明涡旋分布的面积更小、更为集中。较大的角速度使帆片有效迎角仍大于椭圆帆片, 从而为机翼提供更多的升力。当迎角增加至α=12°时,翼尖涡涡通量小于椭圆帆片机翼,没有产生翼尖失速,对机翼仍提供正升力。其主要原因在于,椭圆帆片的环量展向分布为常数,而梯形帆片环量的展向分布从翼根至约80%展长(与展弦比有关)处逐渐增加到最大值,且略大于椭圆翼面环量;但从80%展长至帆片梢部,环量迅速下降并低于椭圆翼面环量[20]。因此,相同迎角下,椭圆帆片梢部升力系数大于梯形帆片,随着迎角增加,会早于梯形帆片形成翼尖失速。另外,迎角增加后,较弱的涡旋强度使梯形帆片诱导的下洗速度也较小。
在相同迎角下,梯形帆片和椭圆帆片翼尖涡系流动形态的差异没有因间隙比的不同而发生明显的改变,使得梯形帆片对机翼升力的贡献均大于椭圆帆片。此外,较大的帆片升力在自由来流方向的投影形成的推力,可抵消部分机翼受到的阻力,这也是梯形帆片机翼总阻力小于椭圆帆片机翼的原因之一,而减阻的最主要原因是梯形帆片翼在相同升力系数下具有更低的诱导阻力。因此,与椭圆帆片翼相比,梯形帆片翼具有更好的增升减阻效果。
这里需要说明的是,尽管在迎角α=2°下梯形帆片机翼的翼尖涡强度和诱导阻力大于椭圆帆片机翼,但在相同升力系数下,梯形帆片机翼的诱导阻力系数小于椭圆帆片机翼(见图 7),两者并不矛盾。
3 结论对安装了椭圆帆片和梯形帆片的机翼气动力的测量,发现了2种机翼在地面效应条件下升力、阻力的差异,通过对翼尖涡静压、涡量分布和涡通量的比较和分析,讨论了机翼气动力产生差异的原因。梯形帆片机翼的升力、阻力特性在各间隙比时均优于椭圆帆片机翼,并且这些优势随着机翼接近地面而不断增强。其主要原因是主翼翼尖处局部气流偏转造成各帆片有效迎角的不同,从而使帆片对主翼产生不同的附加升力贡献。从翼尖涡量分布中可初步推断,随着主翼迎角的增加,梯形帆片的升力变化比较平缓,并呈增加趋势;而椭圆帆片升力改变更为剧烈,从小迎角时帆片的负升力到较大迎角时的帆片翼尖失速,因此对主翼的增升贡献弱于梯形帆片。而尽管梯形帆片翼尖涡的涡量较高,但涡通量较小涡旋强度较弱,从而具有更小的诱导阻力。同时,梯形帆片升力在自由来流方向的推力也能够更多地抵消部分机翼阻力,造成总阻力低于椭圆帆片翼。
上述结论主要源于对翼尖涡静压、涡量分布等展向流动的分析,尚需要各帆片翼面流动分离特性数据的佐证,目前课题组正在开展该方向的实验研究,以便从不同的角度对翼尖帆片增升减阻机理进行深入探讨。
| [1] | Newman B G. Soaring and gliding flight of the black Vulture[J]. Journal of Experimental Biology , 1958, 35 : 280–285. |
| [2] | Tucker V A. Aerodynamics of gliding flight in a Harris' hawk, Parabuteo Unicinctus[J]. Journal of Experimental Biology , 1990, 149 : 469–489. |
| [3] | Tucker V A. Pitching equilibrium wing span and tail span in a gliding Harris' hawk, Parabuteo Unicinctus[J]. Journal of Experimental Biology , 1992, 165 : 21–41. |
| [4] | Tucker V A. Drag reduction by wing tip slots in a gliding Harri's Hawk, Parabuteo Unicinctus[J]. Journal of Experimental Biology , 1993, 198 : 775–781. |
| [5] | Tucker V A. Gliding birds:reduction of induced drag by wing tip slots between the primary feathers[J]. Journal of Experimental Biology , 1993, 180 : 285–310. |
| [6] | Spillman J J, Allen J E. The use of wing tip sails to reduce vortex drag[J]. Aeronautical Journal , 1978, 82 (813) : 387–395. |
| [7] | Spillman J J, McVitie M. Wing tip sails which give lower drag at all normal flight speeds[J]. Aeronautical Journal , 1984, 88 (878) : 362–369. |
| [8] | 陈明岩, 齐孟卜. 翼尖帆片的增升减阻研究[J]. 航空学报 , 1994, 15 (6) : 641–646. Chen M Y, Qi M B. The research of increased lift and reduced drag for wing-tip sails[J]. Acta Aeronautica et Astronautica Sincia , 1994, 15 (6) : 641–646. |
| [9] | 齐孟卜, 陈明岩. 翼尖附近流场研究及帆片减阻机理[J]. 气动实验与测量控制 , 1995, 9 (1) : 38–45. Qi M B, Chen M Y. The study of flow field near the wing tip and the mechanism of drag reduction for wing tip sails[J]. Ae-rodynamic experiment and measurement & Control , 1995, 9 (1) : 38–45. |
| [10] | Smith M J, Komerath N, Ames R, et al. Performance analysis of awing with multiple winglets[R]. AIAA-2001-2407, 2001. |
| [11] | Miklosovic D S. Analytic and experimental investigation of dihedral configurations of three-winglet planforms[J]. Journal of Fluids Engineering , 2008 : 130-071103. |
| [12] | Catalano F M, Ceron-Muñoz H D. Experimental analysis of the aerodynamic characteristics adaptive of multi-winglets[R]. AIAA-2005-1231, 2005. |
| [13] | Cosin R, Catalano F M, Correa L G N, et al. Aerodynamic analysis of multi-winglets for low speed aircraft[C]. 27th International Congress of the Aeronautical Sciences, 2010. |
| [14] | Srikanth G, Surendra B. Experimental investigation on the effect of Multi-winglets[J]. International Journal of mechanical & Industrial Engineering , 2011, 1 (1) : 43–46. |
| [15] | Yang K, Xu S J. Wing tip vortex structure behind an airfoil with flaps at the tip[J]. Science China Physics, Mechanics & Astronomy , 2011, 54 (4) : 743–747. |
| [16] | 杨可, 黄浩, 徐胜金. 组合小翼和翼梢喷流对翼尖涡的影响实验研究[J]. 实验流体力学 , 2014, 28 (6) : 27–38. Yang K, Huang H, Xu S J. Experimental study of effects of multi-winglets and tip blowing upon wingtip vortex[J]. Journal of Experiments in Fluid Mechanics , 2014, 28 (6) : 27–38. |
| [17] | Withers P C, Timko P L. The significance of ground effect to the aerodynamics cost of flight and energetics of the black ski-mmer[J]. Journal of Experimental Biology , 1977, 70 : 13–26. |
| [18] | Hainsworth F R. Induced drag savings from ground effect and formation flight in brown pelicans[J]. Journal of Experimental Biology , 1988, 135 : 431–444. |
| [19] | 江永泉. 飞机翼梢小翼设计[M]. 北京: 航空工业出版社 ,2009 . Jiang Y Q. Design of aircraft winglet[M]. Beijing: The Publishing Company of Aviation Industry , 2009 . |
| [20] | 杨岞生, 俞守勤. 飞行器部件空气动力学[M]. 北京: 航空工业出版社 ,1987 . Yang Z S, Yu S Q. Aerodynamics of aircraft components[M]. Beijing: The publishing company of aviation industry , 1987 . |
| [21] | Byelinskyy V G, Zinchuk P I. Hydrodynamical characteristics of an ekranoplane wing flying near the wavy sea surface[C]//RTO Meeting Proceedings, 1991:1-12. |
| [22] | 章旷.机翼地面效应拖曳水槽实验研究[D].上海大学, 2016. |
| [23] | Kate J, Plotkin A. Low-speed aerodynamics--from wing theory to panel methods[M]. McGraw-Hill Inc: , 1991 . |



