气液两相流常见于冶金、石油、动力、化工、能源、管道运输及制冷制药等领域,在工业生产与科学研究中具有重要作用,在工业过程中也伴随着许多经济与安全问题,因此对两相流活动过程机理状态的描述、解释以及流动过程中相关参数的准确测量具有重要意义,也是现代工业系统中亟待解决的一道难题。随着工业水平的不断提高,两相流涉及的领域越来越广泛,对工业过程控制精度的要求也在不断提高。在目前工业生产中,由于一些传统的流量测量方式及模型无法适用于两相流特有的波动性和复杂的流动形态,使得其相关参数的测量方法多处于研究阶段,离实际应用尚有一定距离[1-2]。
气液两相流过程参数的检测策略随工况与对象属性的变化而变化,可以利用的物理现象与关系有很多,因此检测方法也多种多样。从测量形式上讲,目前常见的检测方法大致可分为直接法和间接法2类,前者可以通过采用传统单相流仪表等方法直接测得待测对象的相关参数,后者则多采用一定的辅助测量值建立待测参数与特征值的关系式,通过模型计算得到[2]。利用传统单相流量计测量气液两相流参数是多相流测量研究与应用的一个重要方向,Skea和Hall指出,虽然这类仪表在检测混合流量时的性能良好,但由于工况和模型的差异,在检测相含率时误差较大[3-4]。从测量原理上讲,气液两相流相关参数的测量方法可以分为分离法和非分离法,前者是将两相流流体分离,利用单相流的测量方法分别获得相关参数,但此类方法受测量设备庞大、系统复杂等因素的限制,需要对取样设备进行更进一步的研究,后者直接利用传统差压式流量计对混合的两相流流体进行测量,传统差压式流量计由于结构简单、性能可靠等特点,一直以来在多相流参数测量中倍受关注。Murdock[5],James[6],Chisholm[7-8],Smith[9], Lin[10], Steven[11]和Steven and Hall[12]等通过理论分析结合实验研究建立了半经验测量模型。采用新技术和方法,Huang等[13]和Meng等[14]将文丘里管与电容、电阻层析成像技术相结合,在实验室中实现了对气液两相流空隙率和流量的测量。
传统差压式流量计是将流向管道中心收缩,通过测量节流件(如孔板和文丘里管)前后的压力降来得到流量数据。近20年出现了一种新型V型内锥流量计,它将原本利用流体进行节流而后收缩到管道中心轴线附近的概念从根本上改变为利用同轴安装在管道中的V形锥体将流体慢慢地进行节流而后收缩到管道的内边壁。与其他传统差压式流量计相比,V锥流量计在压损、重复性、量程比和长期工作稳定性等方面表现出一定的优势,实验分析表明其可用于两相流的流型识别和参数测量[15-18],但由于V锥流量计的内锥形状较为复杂且节流件尾部钝体会使流体产生流动分离,产生旋涡并造成较大压力损失等问题使其应用受到一定的限制。本文作者在V锥流量计的基础上设计了一种具有对称结构的双锥流量计[19],利用理论模型较成熟的差压原理开展气液两相流参数的测量,并根据气液两相流固有的波动特性提取相关特征值,分析其与分相含率等参数的关系[20-22],探寻气液两相流的参数测量新型测量方法并开展实验分析和研究,为气液两相流在工业过程参数准确检测及新型流量计商业化奠定基础。
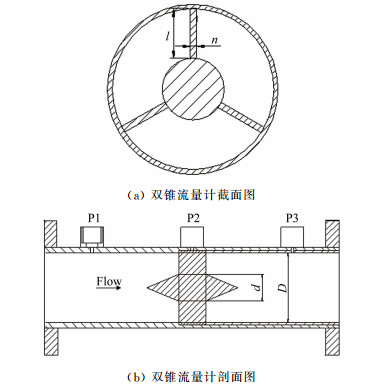
1 测量原理 1.1 流量计结构双锥流量计为一新型内锥流量计,节流单元基本结构如图 1所示,包括测量管段、取压口和节流锥体。图 1(b)为双锥流量计剖面图,P1、P2、P3分别为3个取压口,P1为上游流体收缩前取压口,P2为节流件喉部最小流通面积处取压口,P3为下游流束稳定时的取压口。本实验研究所需的双锥流量计差压信号是从P1与P2口获得的前差压。利用P2与P3可获得双锥流量计的后差压。节流锥体是双锥流量计的核心部件,主要包括锥体和锥体支架结构2部分,如图 2所示。双锥流量计的锥体由前后2个锥角相等的对称锥体构成,3个片状支架和1个管环构成锥体支架结构,节流锥体可通过支架结构固定在管道中心并与管道同轴,将与管道内径相同的管环安装在实验管道中。
|
| 图 1 双锥流量计结构示意图 Fig.1 Scheme of the meter structure |

|
| 图 2 双锥流量计节流锥体 Fig.2 Throttling cone of double-cone flowmeter |
本次研究所设计的双锥流量计锥体前后锥角均为45°,中部圆柱体长度20mm。D为管道内径,d为节流锥体在喉部处直径,α为对称锥体的锥角。图 1(a)为管道最小流通面积处的截面图,双锥体采用三角结构固定于管道内,既能使双锥承受较大的冲击又可以保证双锥与管道内圆的同轴度,同时足够薄度的支撑叶片也可以最大程度减小对流体的扰动。
1.2 基本测量模型双锥流量计的工作原理是基于流体在一密封管道中的能量守恒原理(伯努利方程)和流动连续性原理。根据流体力学的相关理论可以推出单相流流量的基本测量模型:
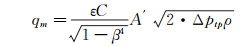 (1)
(1)
式中:Δptp为差压;ρ为单相流流体的密度;C为流出系数;A′为流束的最小流通面积(A′=πβ2D2/4);ε为流体的可膨胀系数,对于不可压缩流体ε=1;β为等效直径比,即流束最小流通面积和管道截面积的比值,β=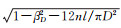
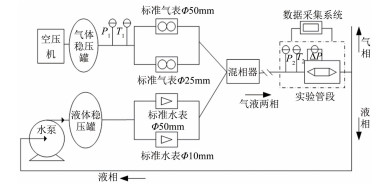
图 3和4分别为双锥流量计气液两相流实验系统实物图和结构简图,实验对象为水平管道内的气/水混合流体。实验设备主要包括数据采集系统和实验管路2大部分:数据采集系统包括数据采集器及采集控制界面;实验管路包括双锥流量计、压力变送器、差压变送器、温度计、标准表以及管道和阀门等设备。

|
| 图 3 多相流实验系统实物图 Fig.3 The picture of experimental facility for multi-phase flow |
|
| 图 4 气液两相流实验系统结构简图 Fig.4 Scheme of the experimental system |
装置的工作流程为:水经过稳压罐后,通过标准水表读取其体积流量,进入混相器;空气压缩机将空气压缩到稳压罐,通过标准气表读取其体积流量,并用温度计和压力表测量此时的气相温度(T1)和压力(p1),最后进入混相器与液相混合;气液两相流经过8m长的直管段,充分混合后进入气液两相实验管段,在此处安装双锥流量计并测量气液两相的混合差压,同时测量双锥流量计前的压力(p2)和温度(T2),采用数据采集系统记录各测量值。
实验中,液体稳压罐和气体稳压罐的稳压范围分别为0.2~0.21MPa和0.39~0.41MPa,标准水表和标准气表参数如表 1,直管段以及实验管段管径为50mm。
| 管径/mm | 流量计类型 | 精度等级 | |
| 标准气表 | 50 | 旋进旋涡流量计 | 1.5 |
| 25 | 旋进旋涡流量计 | 1.5 | |
| 标准水表 | 50 | 电磁流量计 | 0.2 |
| 10 | 电磁流量计 | 0.2 |
考虑到不同等效直径比的双锥流量计具有不同的测量特性,选择不同的直径比可分析双锥流量计各自不同特性,从而获得与直径比相关的关键参数,因此选用2个不同等效直径比(0.424、0.586)的双锥流量计进行实验,其流出系数分别为0.9672和0.9685。双锥流量计的差压信号由应变式差压变送器进行测量,其量程为0~64kPa,输出电流信号4~20mA,精度等级为0.25%FS。
3 分相含率测量模型在气液两相流的测量中,分相含率是一个重要的参数,重点测量对象为气相的相含率,包括体积含气率、截面含气率(空隙率)和质量流量含气率(干度)。其中体积含气率和干度的关系如下式:
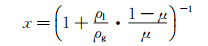 (2)
(2)
式中:μ为体积含气率;ρg为气相密度;ρl为液相密度。
气液两相流在流动过程中存在波动性,根据前人的实验研究结果,此波动信号与气液两相流的流型、分相含率等重要测量参数具有一定的相关性,因此可以通过分析从差压波动信号中提取的特征值建立气液两相流分相含率的测量模型,从而实现对气相含率等参数的在线测量。
气液两相流通过差压式流量计时的瞬时差压和瞬时流量之间也符合时间平均值的关系式,因此:
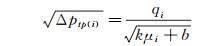 (3)
(3)
式中:i为某个瞬时时刻;Δptp(i)为瞬时差压;μi为瞬时体积含气率;qi为瞬时流量;k、b是与节流元件结构和两相流流体物性有关的系数。
定义脉动振幅为差压瞬时值和时均值之差,其均方根为:
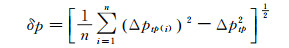 (4)
(4)
式中:n为差压瞬时值采样个数;δp为差压信号的脉动振幅。
定义无量纲参数R=δp/Δptp,则:
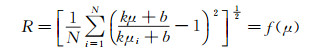 (5)
(5)
理论上R是μ的单值函数,可通过实验差压时均值和差压脉动幅值计算出气相体积含率μ。
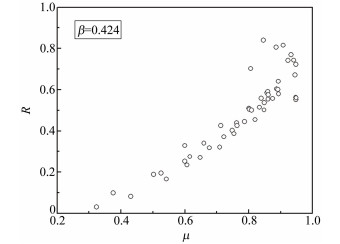
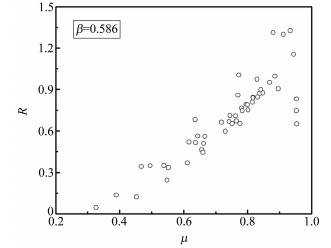
实验所用水平管道管径为50mm,进行气液两相流实验并采集差压波动信号,图 5和6为等效直径比为0.424和0.586的双锥流量计无量纲参数R与体积含气率μ的数值点分布。
|
| 图 5 β=0.424无量纲参数R与气相体积含率μ关系图 Fig.5 Relationship of the nondimensional parameter R with the gas volume fraction μ with β=0.424 |
|
| 图 6 β=0.586无量纲参数R与气相体积含率μ关系图 Fig.6 Relationship of the nondimensional parameter R with the gas volume fraction μ with β=0.586 |
由图 5和6可知,对于双锥流量计,波动幅度参数R随着体积含气率呈现先增大后减小的趋势。当体积含气率小于0.3时,差压的波动幅度参数很小;然后随着体积含气率的增大,差压的波动幅度值增大,并在0.85左右达到最大值。根据流体在管道中流动的实际情况,当流体为单相(即全为液相μ=0,全为气相μ=1)时,流动是较为平稳的,应有R≈0,因此可假设R与μ符合如下关系:
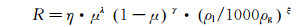 (6)
(6)
式中:η、λ和ξ为待定系数,可由实验获得。一系列的实验表明,R值还受流体密度的影响,因此引入修正项(ρl/1000ρg)ξ,由此定义新的无量纲参数R′,
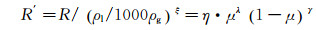 (7)
(7)
| β | η | λ | γ | ξ |
| 0.586 | 10.319 | 3.798 | 0.624 | 0.981 |
| 0.424 | 3.511 | 3.237 | 0.37 | 0.858 |
双锥流量计作为一种新型差压式流量计,在结构上与传统标准差压流量计具有一定的差异,现有模型的一些关键参数无法适用,需寻求新的模型参数。
Murdock用汽水、气水和天然气水混合物经过大量实验并对理想分相流模型进行修正后得到孔板气液两相流流量计算模型:
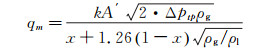 (8)
(8)
式(8)可改写为如下形式:
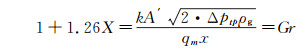 (9)
(9)
式中,X为Lockhart-Martinelli常数,可由下式计算:
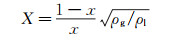 (10)
(10)
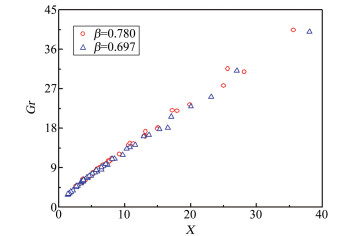
式(9)等式的右边可认为是准气相流量比,根据双锥流量计气液两相流的测量数据,分析X与气相流量比的关系,如图 7所示。
|
| 图 7 Lockhart-Martinelli常数与准气相流量比的关系 Fig.7 Relationship between Lockhart-Martinelli constant and gas flowrate ratio |
分析图 7中的数据,可认为Lockhart-Martinelli常数与准气相流量比存在如下线性关系:
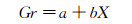 (11)
(11)
待定系数a和b如表 3中所示。
| a | b | |
| β=0.424 | 2.1508 | 1.0314 |
| β=0.586 | 2.026 | 1.0875 |
与式(8)类比,结合式(11),对于该双锥流量计测量气液两相流,改进的Murdock模型可表示为:
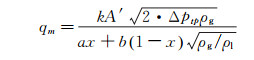 (12)
(12)
Δptp是差压波动信号的均值。
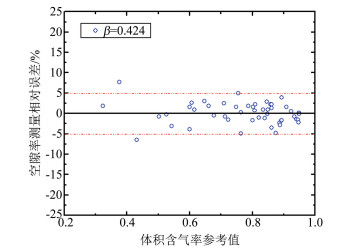
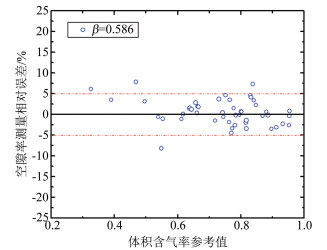
5 实验与结果分析 5.1 气相含率测量实验在体积含气率为0.32~0.96范围内进行,对流体流经双锥流量计时所产生的前差压进行了采集,提取差压波动信号中的特征值R′,通过模型式(7)计算得出体积含气率值,模型测量误差如图 8和9所示,体积含气率的相对误差基本在±5%以内。
|
| 图 8 β=0.424体积含气率模型测量误差 Fig.8 Relative errors of the measured gas volume fraction with β=0.424 |
|
| 图 9 β=0.586体积含气率模型测量误差 Fig.9 Relative errors of the measured gas volume fraction with β=0.586 |
气液两相流流量实验测量以水和空气为介质,其中水和空气的质量流量范围分别为1.233~6.581kg/s和0.006~0.04kg/s。水稳压为0.2MPa,气源稳压0.4MPa,干度范围0.001~0.03,环境温度20.5℃。NI数据采集卡采集差压波动信号,提取其特征值并通过公式(7)和(2)计算得到质量流量含气率x,流量值可通过公式(12)计算得到。
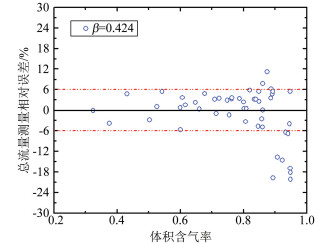
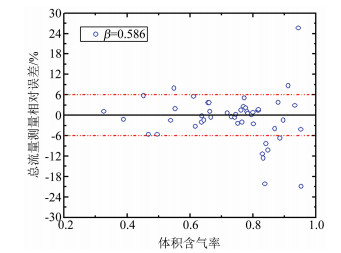
实验测量了气液两相流的总流量及液相、气相的分相流量,在图 10和11中给出了总流量的测量误差,总质量流量的参考值为气相和液相混合前的流量值之和。测量误差结果显示,在实验范围内所采用的体积含气率测量模型和改进的Murdock流量测量模型对气液两相流总流量测量具有较好的适用效果,测量结果相对误差基本可以控制在±6%以内。值得提出的是,当气相体积含率大于0.8时,两相流处于塞状流向环状流的过渡段,流型变化较为复杂,使得测量精度有所下降。
|
| 图 10 β=0.424总流量测量相对误差 Fig.10 Relative errors of total mass flowrate with β=0.424 |
|
| 图 11 β=0.586总流量测量相对误差 Fig.11 Relative errors of total mass flowrate with β=0.586 |
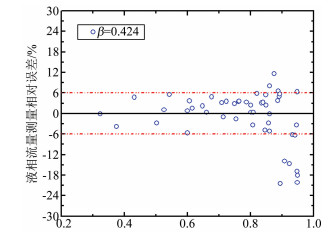
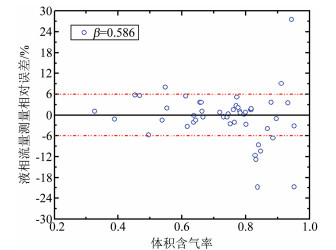
总流量测量相对误差图中可看出,对于气液两相流,其分相流的参数测量具有重要的工程意义。可以根据公式(7)和测量出的体积含气率值由公式(2)得到干度值,从而实现对气液两相流的分相流测量。液相流量测量误差如图 12和13所示,在实验范围内的相对误差基本在±6%以内,说明该测量模型在该工况下具有较好的测量效果。因为在实验所用气液两相流中,气体在总流量中所占的比例较小,所以液相流量测量误差分布结果与总流量相似。
|
| 图 12 β=0.424液相流量测量相对误差 Fig.12 Relative errors of measured liquid mass flowrate with β=0.424 |
|
| 图 13 β=0.586液相流量测量相对误差 Fig.13 Relative errors of measured liquid mass flowrate with β=0.586 |
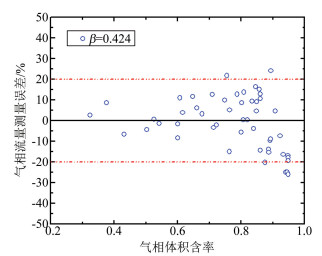
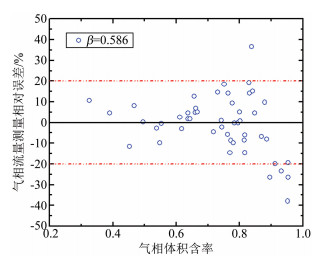
实验对气相流量进行了测量,其测量结果如图 14和15所示。测量误差结果显示,忽略粗大误差后的气相流量测量误差在±20%以内,该误差远大于液相和总流量的测量误差,分析认为在本实验中的两相流干度仅在0.001~0.03范围内,不同于湿蒸气和高干度的实验工况,对体积含气率或干度的微小测量误差会导致对气相流量测量结果的较大偏差。
|
| 图 14 β=0.424气相流量测量相对误差 Fig.14 Relative errors of measured gas mass flowrate with β=0.424 |
|
| 图 15 β=0.586气相流量测量相对误差 Fig.15 Relative errors of measured gas mass flowrate with β=0.586 |
本文将一种新型的双锥流量计用于气水两相流的测量,研究了2个不同等效直径比的双锥流量计对气相体积含率、总流量及分相流量的测量性能。对双锥流量计上的差压波动信号时间序列进行了分析,利用其特征值建立了气水两相流气相含率的关系模型。应用该模型对气相体积含率进行测量,在实验范围内,气相体积含率测量相对误差在±5%以内。利用Lockhart-Martinelli常数建立了双锥流量计气液两相流总流量测量模型,可对总流量和液相流量进行有效的测量,测量结果的相对误差在±6%以内。在干度很小的情况下,气相流量的测量相对误差较大。与V锥流量计在气液两相流相关参数的测量结果(气相体积含率已确定的条件下,两相流总质量流量的相对误差基本在±5%内)相对比表明[17],双锥流量计可获得与V锥流量计相当的精度,且在减小流体扰动、降低压力损失和抗压力冲击等方面更具有优势。
| [1] | 林宗虎, 王栋, 王树众, 等. 多相流的近期工程应用趋向[J]. 西安交通大学学报 , 2001, 35 (9) : 886–890. Lin Z H, Wang D, Wang S Z, et al. Recent trend towards engineering application of multiphase flow[J]. Journal of Xi'an Jiao Tong University , 2001, 35 (9) : 886–890. |
| [2] | 谭超, 董锋. 多相流过程参数检测技术综述[J]. 自动化学报 , 2013, 39 (11) : 1923–1932. Tan C, Dong F. Parameters measurement for multiphase flow process[J]. Acta Automatica Sinica , 2013, 39 (11) : 1923–1932. DOI:10.3724/SP.J.1004.2013.01923 |
| [3] | Skea A F, Hall A R W. Effects of gas leaks in oil flow on single-phase flowmeters[J]. Flow Measurement and Instrumentation , 1999, 10 (3) : 145–150. DOI:10.1016/S0955-5986(98)00055-7 |
| [4] | Skea A F, Hall A R W. Effects of water in oil and oil in water on single-phase flowmeters[J]. Flow Measurement and Instrumentation , 1999, 10 (3) : 151–157. DOI:10.1016/S0955-5986(98)00054-5 |
| [5] | Murdock J W. Two-phase flow measurement with orifices[J]. Journal of Basic Engineering , 1962, 84 (4) : 419–433. DOI:10.1115/1.3658657 |
| [6] | James R. Metering of steam-water two-phase flow by sharp-edged orifices[J]. Proceedings of the Institution of Mechanical Engineers , 1965, 180 (23) : 549–572. |
| [7] | Chisholm D, Rooney D H. Pressure drop during steam/water flow through orifices[J]. Mechanical Engineering Science , 1974, 16 (5) : 353–355. DOI:10.1243/JMES_JOUR_1974_016_065_02 |
| [8] | Chisholm D. Two-phase flow through sharp-edged orifices[J]. Mechanical Engineering Science , 1977, 19 (3) : 128–130. DOI:10.1243/JMES_JOUR_1977_019_027_02 |
| [9] | Smith L T, Murdock J W, Applebaum R S. An evaluation of exisiting two-phase flow correlations for use with ASME sharp edge metering orifices[J]. Journal of Engineering for Power , 1977, 99 (3) : 343–347. DOI:10.1115/1.3446500 |
| [10] | Lin Z H. Two-phase flow measurements with sharp-edged orifices[J]. International Journal of Multiphase Flow , 1982, 8 (6) : 683–693. DOI:10.1016/0301-9322(82)90071-4 |
| [11] | Steven R N. Wet gas metering with a horizontally mounted Venturi meter[J]. Flow Measurement and Instrumentation , 2002, 12 (s5-6) : 361–372. |
| [12] | Steven R, Hall A. Orifice plate meter wet gas flow perfor-mance[J]. Flow Measurement and Instrumentation , 2009, 20 (4-5) : 141–151. DOI:10.1016/j.flowmeasinst.2009.07.001 |
| [13] | Huang Z Y, Xie D L, Zhang H J, et al. Gas-oil two-phase flow measurement using an electrical capacitance tomography system and a Venturi meter[J]. Flow Measurement and Instrumentation , 2005, 16 (2-3) : 177–182. DOI:10.1016/j.flowmeasinst.2005.02.007 |
| [14] | Meng Z Z, Huang Z Y, Wang B L, et al. Air water two phase flow measurement using a Venturi meter and an electrical resistance tomography sensor[J]. Flow Measurement and Instrumentation , 2010, 21 (3) : 268–276. DOI:10.1016/j.flowmeasinst.2010.02.006 |
| [15] | 陈飞, 孙斌, 王二朋, 等. 不同节流装置测量气液两相流的动态特性研究[J]. 实验流体力学 , 2012, 26 (1) : 55–60. Chen F, Sun B, Wang E P, et al. Research on the dynamic characteristics of gas-liquid two phase flow measurement with different throttle devices[J]. Journal of Experiments in Fluid Mechanics , 2012, 26 (1) : 55–60. |
| [16] | 孙斌, 刘彤, 赵鹏. 基于EE MD气液两相流差压信号时频分析[J]. 实验流体力学 , 2014, 28 (5) : 47–52. Sun B, Liu T, Zhao P. Time-frequency analysis on differential pressure signal of two-phase flow based on EEMD[J]. Journal of Experiments in Fluid Mechanics , 2014, 28 (5) : 47–52. |
| [17] | 胡俊, 董峰. 基于V型内锥流量计测量气/水两相流的研究[J]. 工程热物理学报 , 2007, 38 (1) : 205–208. Hu J, Dong F. Research on measurement of air/water two-phase flow based on V-cone flowmeter[J]. Journal of Engineering Thermophysics , 2007, 38 (1) : 205–208. |
| [18] | Zhang F S, Dong F, Tan C. High GVF and low pressure gas liquid two-phase flow measurement based on dual-cone flowmeter[J]. Flow Measurement and Instrumentation , 2010, 21 (3) : 410–417. DOI:10.1016/j.flowmeasinst.2010.06.004 |
| [19] | Xie D L, Zhu Y, Tao S. Flowrate measurement of gas/liquid two-phase flow base on the double-cone flowmeter[C]. Conference Record-IEEE Instrumentation and Measurement Technology Conference, 2011:1-4. |
| [20] | Xu L J, Xu J, Dong F, et al. On fluctuation of the dynamic differential pressure signal of Venturi meter for wet gas metering[J]. Flow Measurement and Instrumentation , 2003, 14 (4-5) : 211–217. DOI:10.1016/S0955-5986(03)00027-X |
| [21] | 仲朔平, 佟云宪, 王文然. 利用孔板差压噪声测量汽水两相流[J]. 清华大学学报(自然科学版) , 1997, 37 (5) : 15–18. Zhong S P, Tong Y X, Wang W R. Double parameter measurement steam-water two-phase flow by using differential pressure noise of orifice[J]. Journal of Tsinghua University(Sci & Tech) , 1997, 37 (5) : 15–18. |
| [22] | Ferreira V C S. Differential pressure spectral analysis for two-phase flow through an orifice plate[J]. The International Journal of Pressure Vessels and Piping , 1997, 73 (1) : 19–23. DOI:10.1016/S0308-0161(97)00029-X |



