超空泡流动现象常见于水中高速鱼雷、潜水艇发射战略战术导弹和利用高速射弹消灭水雷等军事技术中,因此一直是国内外的热门研究课题之一[1-2],本课题组对此也进行了研究[3-5]。超空泡带迎角地穿过自由面问题源于从潜水艇鱼雷发射管发射战斧式巡航导弹,为此美国海军进行了大量的实验[6]。我国在这方面的研究还不够充分,无论是实验还是数值计算。附着在潜射导弹上的空泡一般是自然空化空泡(Natural Cavitation),空泡内部压力约为水的饱和蒸气压(2.35×103Pa)。导弹出水时,空泡与压力为1个标准大气压(105Pa)的空气接触,因此空气必然进入空泡,使其成为充气空泡(Ventilated Cavitation)。然而必须明确的是,与用人工方法给空泡充气的过程不同(诸如高速鱼雷),在出水时空泡获得的充气仍然是在自然状态下进行的。
胡影影等人[7]使用改进的Youngs算法对航行体在自由面附近出水进行了数值模拟,着重研究了韦伯数We和弗汝德数Fr在出水运动过程中对液面的影响。黄海龙等人[8]通过划分结构网格,对圆盘空化器进行了三维数值仿真,模拟中应用了k-ε湍流模型求解N-S方程,通过改变不同的空化数大小,得到相应的计算参数,然后将计算参数的结果与前人的经验公式相对比。王一伟等人[9]通过将结构力学和计算流体力学2种方法相结合,建立了弹体在带迎角出水时的数值模拟方法。Chu等人[10]模拟了圆柱航行体带空泡的出水过程,根据测量得出的压力数据能够得出空泡溃灭的大致时间和位置,发现空泡溃灭时会产生水拍打液面的现象,通过这种方式产生了高压,并且通过实验拍摄的图片与数值模拟产生的尾部空泡相对比,发现数值模拟产生的尾空泡更小一点;据此推测,这可能是由于在实际压缩气体喷射航行体的过程中,有部分气体会沿着航行体喷出,从而使实验中的尾空泡变得更大一些。张军等人[11]和赵蛟龙等人[12]分别对低速全沾湿物体和局部超空泡倾斜出水流场进行了PIV和高速摄影研究。
本课题组进行了细长钉体(横截面尺寸约为1mm)在小迎角α=5.5°~10°范围的出水实验和数值模拟[13]。本文将报道直径为6mm的钝体在较大迎角α=57°下的出水实验和数值模拟。这里使用“钝体”一词,是为了与以前的尖头钉体有所区别,但其长径比为8~12,实际也属于细长体。
1 实验装置与方法图 1示出了实验装置。一台倾斜放置的一级轻气炮装置(见图 1中的部件4~12)向水箱自下而上地发射试验模型,模型冲击进入水箱1产生超空泡,然后穿过自由面2。圆柱体模型直径为6mm,长度分别为48、60和72mm(质量为3.69~5.50g),材料为铝镁合金。使用Photron Fastcam SA5高速摄影机记录超空泡穿过自由面的过程,然后将照片导入AutoCAD软件;测量位移等数据,每点测量3次,取平均值,最后计算出速度、阻力系数等物理量。根据冲击工程惯例,定义超空泡运动方向与水平液面的垂直方向之间的夹角为出水迎角α。有关实验技术的更多细节,可参见文献[14-15]。

|
| 图 1 超空泡物体倾斜出水发生装置示意简图 Fig.1 Sketch of the generating device of the supercavitating vehicle 1观测水箱; 2液面; 3橡胶挡板; 4小车支撑架; 5发射管; 6小车轨道; 7小车; 8管阀连接器; 9电磁阀; 10缸阀连接器; 11高压气缸; 12储气罐 |
图 2示出了长径比为10的平头圆柱体带迎角地穿过自由面的高速摄影照片。超空泡在图 2(1)中出现在视场中的左下角,其速度为V0=23.02 m/s;流场的标尺也在图 2(1)中给出。超空泡向右上方运动,逐渐靠近自由面(见图 2(2)~(7))。在图 2(8)所示的时刻,超空泡与自由面接触;然后在图 2(9)~(12)的时间段里,圆柱体伸出水面。从图 2(13)所示的时刻开始,圆柱体彻底脱离水面,进入空气中自由飞行。超空泡与自由面倾斜地相互作用后(见图 2(9)~(10)),出现了2个特殊的现象:一是在水面上沿着运动方向、即沿着超空泡的轴线,出现了不对称的水花。二是负压的超空泡从大气中倒吸空气,形成了充气空泡。如图 2(11)~(15)所示,水花先在轴线的上部形成并向右上方运动,水花头部的速度与圆柱体在空中的飞行速度接近(水花头部速度大于物体速度也是可能的)。从图 2(16)开始,轴线下部的水花才明显地形成,然后逐渐发展,与上部水花合并形成喇叭口的水花(见图 2(23)~(24))。水花以如此的方式形成,就使得空泡在水面上难以产生表面闭合(Surface Closure),空气被吸入负压的空泡中,因此空泡能在自由面附近长期存留而不会破灭。从图 2(11)~(24),空泡已存活了20ms的时间,而且空泡的最大直径从32mm增加到了46mm,尽管空泡后面的空化尾迹已经十分明显(见图 2(21)~(24))。如果对比本文第4节的数值计算结果,就可以理解上述的自然空化空泡向充气空泡转化的过程。

|
| 图 2 平头圆柱体诱导的超空泡带迎角地穿过自由面的高速摄影照片。模型长径比为10,初速度V0=23.02m/s,相邻两幅照片之间的时间间隔Δt=10/7ms,出水迎角α =57°。 Fig.2 High speed photographs of the inclined water-exit of a flat head cylinder |
图 3(a)和(b)分别给出了测得的长径比为8、10和12的圆柱体的速度V随时间t的变化,以及阻力系数CD随空化数σ的变化。其中空化数σ是物体在每个时刻下计算出的,因此图 3(b)的横轴不需用时间t表示。从图 3(a)中可以看出,3个圆柱体在出水前后,即在t=10.00、12.86和14.27ms时刻,其速度都有一个跃增。这是因为物体从水中突然进入空气中甩负荷的缘故[5]。如果在穿过水面前后,在水中和在空气中的物体速度分别为Vw和Va,那么实验得到的Va/Vw=1.06~1.11。图 3(b)中给出的σ的最大值即是出水前的空化数,3个圆柱体的该空化数分别为σ=1.134、0.969和0.496。

|
| 图 3 超空泡物体的速度和阻力系数的测量结果 Fig.3 Measured velocity and drag coefficient of the supercavitating body |
圆柱体在水中和空气中的运动方程分别为:
 (1)
(1)
 (2)
(2)
式中:m、aw、A、CD分别为物体的质量、加速度、截面积和阻力系数,ρ、g和α分别是流体密度、重力加速度和出水迎角,下标w和a分别表示在水中和空气中。将两式相除,整理后得到
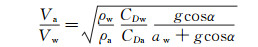 (3)
(3)
根据图 3(a)可知,物体在出水前呈单调地减速,计算出的3个工况的加速度非常接近,其绝对值为1.04×103m/s2。运动物体在空气中的雷诺数Re=(5.93~7.01)×103,所以物体在空气中的阻力系数CDa约为1.00[16-17]。参考图 3(b),得知在出水前,物体的阻力系数CDw约为0.90~1.10,因此不妨认为CDw/CDa →1。然后从式(3)中算出Va/Vw=2.03。这个理论值大于实验值,这是因为物体刚出水时,虽然上部已露在空气中,但下部仍与水沾湿,此时阻力较大,会出现CDw/CDa < 1,这样计算出的Va/Vw的理论值会接近于实验值。
根据图 3(a)还可知,物体在出水后基本上保持恒速,因此式(2)中本应该出现的加速度项maa→0。上述有关出水前后物体速度变化的机理,如果从动量守恒定律来分析,就可以理解为:既然空泡引起的附加质量m*在出水后自动消失,而物体在穿过自由面时又没有受到其他外力作用,那么显然(m+m*)Vw=mVa。所以,
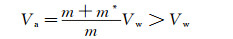 (4)
(4)
本文需要关注水中物体产生的空泡,所以在物体周围的网格划分较为密集,对物体周围加密时采用了尺寸函数,定义开始尺寸为1mm,增长率为1.2,最大尺寸为2mm。用Gambit软件对计算区域进行划分网格,且对物体周围进行局部加密,计算区域为1500mm×400mm,本文采用三角形非结构网格,网格总数为508 499。边界条件设置为:计算区域入口设置为wall边界,出口设置为压力出口,航行体边界设置为wall边界,如图 4所示。
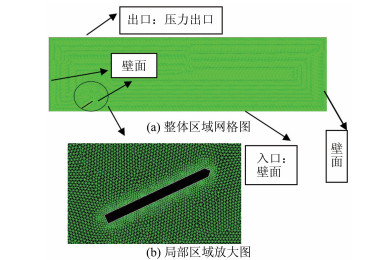
|
| 图 4 网格划分结构图 Fig.4 The grid division |
将模型导入到Ansys14.0中,进行计算参数设置,具体步骤为:计算采用VOF多相流模型(水、空气和水蒸气),使用压力基求解器,计算考虑了重力的影响,重力加速度设置为-9.81m/s2。由于超空泡在运动过程中对时间的依赖性很强,所以选择非定常流动,空化模型采用的是Schnerr and Sauer模型,水的饱和蒸气压为3540Pa。求解方法采用SIMPLE算法。网格运动过程中的更新方法为弹簧近似光滑模型和网格重构模型实现,将编好的profile文件导入Ansys14.0中实现航行体的变速运动。
4 计算结果图 5给出了水下超空泡物体倾斜出水过程相图的数值模拟结果,包括超空泡从生长到消失的全过程。已计算了各种不同的工况[15],这里只给出一组典型的数据。空泡开始出生时的位置主要发生在物体的尾部和肩部(见图 5(1)~(2)),随着时间的增大,空泡慢慢生长,直到将物体完全包裹、形成超空泡(见图 5(3)~(6))。然后物体带超空泡继续前进,直到穿出水面,并且在物体尾部带出水花(见图 5(15)~(16))。数值计算揭示了当水下超空泡物体接近自由面时(见图 5(5)~(8)),水面必然抬升隆起的、由水的不可压缩性所导致的后果。数值计算的另一个有意思的结果是,从图 5(14)~(16)的不到2ms的时间里,超空泡一接触水面就消失了,大大小于在图 2的实验中观察到的、大于20ms的超空泡的寿命。这是因为计算软件中的空化模型是完全自然空化模型,没有考虑到空泡从大气中吸取空气的机理。因此在今后建立充气空泡模型并改进软件的算法是十分必要的。另外,在第2节中讨论式(3)的计算结果时,认为物体刚出水时上半部分露在空气中,而下半部分与水沾湿,这个推断也被数值计算证实了。今后要注意的是:根据空化数的定义,当空泡浸没在水面下时,空泡壁面上的压力是水的饱和蒸气压;当空泡露出水面进行通气后,空泡壁面上的压力是大气压,有限体积算法不一定能处理好这种问题。Young和Savander[18]用边界元方法计算了部分浸没的空泡以及表面划水螺旋桨叶片的流场,值得参考。

|
| 图 5 空泡倾斜出水过程的数值模拟(物体长径比为12) Fig.5 Numerical results of water exit of the inclined supercavity |
图 6给出了3个不同时刻水下物体周围的压力图(压力的单位是Pa),其相图分别是图 5(3)、(4)和(8)。从图 6(a)中可以看出,在t=2.57ms时,超空泡离自由面还较远,此时从相对应的压力图中可以看出,物体的周围压力对称分布。随着超空泡靠近自由面(见图 6(b)和(c)),物体头部下方的压力比上方大。在研究浅水区的超空泡运动特性时,也发现了空泡下部的压力大于上部的压力[19]。这说明当超空泡靠近自由面时,浮力发挥作用,这对空泡后期的发展,包括形状和溃灭特性,产生一定的影响。
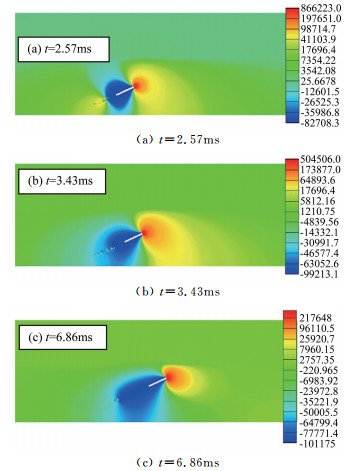
|
| 图 6 不同时刻的水下物体周围的压力图 Fig.6 Pressure diagram around the underwater body |
(1) 超空泡倾斜地与自由面相互作用时,会形成非轴对称的、开口喇叭形的水花,因此原来处于负压的空泡更容易地吸取大气中的空气,空泡从自然空化向充气空泡转变,空泡寿命增加(大于20ms)。
(2) 物体出水前后,速度有一跃增,速度增加率达到6%~11%。通过分析运动方程,从理论上证明了当物体从水中进入空气中时,其速度的确是增加的。运用动量守恒定律,也得出相同结论。对于长径比为10的物体,如图 3(a)中所示的、在t=21.43ms时刻出现的二次增速,是由测量误差造成的;更多的测量结果,可见文献[15]。
(3) 当水中超空泡物体接近自由面时,自由面将隆起抬高,这是后期表面波浪形成的初始原因;自由面对超空泡的影响之一,是空泡下部的压力大于上部的压力。严格地说,用本文的方法产生的超空泡里,会夹带空气的进入。但是,实验中发射管出口离水箱侧面隔膜较近,这样对于空气进入有抑制作用。而数值计算的空泡形状与实验结果比较接近,说明即使有空气进入,其量也是有限的。
| [1] | Sarajam B. Experimental and numerical investigation of an unsteady supercavitating body[J]. Ocean Engnieering , 2013, 59 : 9–14. DOI:10.1016/j.oceaneng.2012.12.021 |
| [2] | 孙士明, 陈伟政, 颜开. 通气超空泡泄气机理研究[J]. 船舶力学 , 2014, 18 (5) : 492–498. Sun S M, Chen W Z, Yan K. Study of gas leakage mechanism of ventilated supercavities[J]. Journal of Ship Mechanics , 2014, 18 (5) : 492–498. |
| [3] | 施红辉, 胡俊辉, 周浩磊. 完全超空泡出水的实验研究及理论分析[J]. 空气动力学学报 , 2014, 32 (4) : 544–550. Shi H H, Hu J H, Zhou H L. Experimental study and theoretical analysis of water exit of a supercavity[J]. Acta Aerodynamics Sinica , 2014, 32 (4) : 544–550. |
| [4] | 贾会霞, 胡俊辉, 施红辉, 等. 出水超空泡的形状与弗劳德数影响的实验研究[J]. 西安交通大学学报 , 2015, 49 (3) : 67–73. Jia H X, Hu J H, Shi H H, et al. Experimental research on the shape of water-exit supercavity and the effect of Froude number[J]. Journal of Xi'an Jiaotong University , 2015, 49 (3) : 67–73. |
| [5] | 陈波, 彭立兵, 施红辉, 等. 细长体出水动力学的实验研究及数值模拟[J]. 实验流体力学 , 2015, 29 (2) : 26–42. Chen B, Peng L B, Shi H H, et al. Experimental and numerical study on hydrodynamics in water-exit of slender body[J]. Journal of Experiments in Fluid Mechanics , 2015, 29 (2) : 26–42. |
| [6] | 陈九锡, 张开荣(译).水弹道学模拟[M].北京:国防工业出版社, 1979. |
| [7] | 胡影影, 朱克勤, 席葆树. 半无限长柱体出水数值模拟[J]. 清华大学学报 , 2002, 42 (2) : 235–238. Hu Y Y, Zhu K Q, Xi B S. Numerical simulation of a semi-infinite cylinder exited from water[J]. J Tsinghua Univ (Sci & Tech) , 2002, 42 (2) : 235–238. |
| [8] | 黄海龙, 黄文虎, 周峰. 圆盘空化器超空泡形态三维数值模拟研究[J]. 兵工学报 , 2008, 29 (1) : 78–84. Huang L H, Huang W H, Zhou F. Numerical simulation on the shape of natural supercavity based on full three dimensional disc-cavitator[J]. Acta Armentarii , 2008, 29 (1) : 78–84. |
| [9] | 王一伟, 黄晨光, 杜特专, 等. 航行体有迎角出水全过程数值模拟[J]. 水动力学研究与进展 , 2011, 26 (1) : 48–57. Wang Y W, Huang C G, Du T Z, et al. Numerical simulation of a submerged body exiting from water with an attack angle[J]. Chinese Journal of Hydrodynamics , 2011, 26 (1) : 48–57. |
| [10] | Chu X S, Yan K, Wang Z, et al. Numerical simulation of water-exit of a cylinder with cavities[J]. J Hydrodynamics , 2010, 22 (5) : 877–881. DOI:10.1016/S1001-6058(10)60045-5 |
| [11] | 张军, 李英浩, 金朋寿. 垂直及斜出水流场的二维及三维TR-PIV试验[J]. 船舶力学 , 2005, 9 (2) : 9–17. Zhang J, Lee Y H, Kim B S. 2D and 3D time resolved PIV experimentson flow field around vertical and inclined water-exit body[J]. Journal of Ship Mechanics , 2005, 9 (2) : 9–17. |
| [12] | 赵蛟龙, 郭百森, 孙龙泉, 等. 细长体倾斜出水的实验研究[J]. 爆炸与冲击 , 2016, 36 (1) : 113–120. Zhao J L, Guo B S, Sun L Q, et al. Experimental study on oblique water-exit of slender bodies[J]. Explosion and Shock Waves , 2016, 36 (1) : 113–120. |
| [13] | 施红辉, 周杨洁, 彭立兵, 等. 伴随空化现象的细长体倾斜穿透水体过程研究[J]. 浙江理工大学学报 , 2016, 35 (3) : 67–72. Shi H H, Zhou Y J, Peng L B, et al. Research on obliquely penetrating water of a slender body accompanying cavitation phenomenon[J]. Journal of Zhejiang Sci-Tech University , 2016, 35 (3) : 67–72. |
| [14] | 王昀, 陈波, 施红辉, 等.一种潜射航行体的可变角度发射的超空泡实验发生装置:中国专利(实用新型), ZL201420012920. 2014-07-09. |
| [15] | 王昀.超空泡航行体倾斜出水过程动力学特性研究[D].杭州:浙江理工大学, 2015. Wang Y. The research of dynamic characteristics in the process of indined water exit of supercavitating vehicle[D]. Hangzhou:Zhejiang Sci-Tech University, 2015. http://cdmd.cnki.com.cn/article/cdmd-10338-1015564262.htm |
| [16] | 夏泰淳. 工程流体力学[M]. 上海: 上海交通大学出版社 ,2006 . Xia T C. Engineering fluid mechanics[M]. Shanghai: Shanghai Jiao Tong University Press , 2006 . |
| [17] | 笠原英司. 水力学[M]. 东京: 产业图书株式会社 ,1994 . |
| [18] | Young Y L, Savander B R. Numerical analysis of large-scale surface-piercing propellers[J]. Ocean Engineering , 2011, 38 : 1368–1381. DOI:10.1016/j.oceaneng.2011.05.019 |
| [19] | 陈波, 胡青青, 施红辉, 等. 离自由面不同深度下水平运动超空泡的数值模拟研究[J]. 浙江理工大学学报 , 2015, 33 (3) : 87–93. Chen B, Hu Q Q, Shi H H, et al. Numerical simulation study of horizontally-moving supercavities at different water depth from the free surface[J]. Journal of Zhejiang Sci-Tech University , 2015, 33 (3) : 87–93. |



