由屋面积雪导致结构损毁的事故时有发生,如1978年美国哈特福德市政体育馆雪灾事故[1],2006年波兰卡托维茨国际展览会厅以及莫斯科巴斯曼室内市场的雪灾事故[2-3]等。在中国,雪灾事故也十分频繁,如2007年东北雪灾,仅辽宁省全省就有92家企业的300多处钢结构厂房遭到不同程度的损坏,许多钢架厂房屋面板结构坍塌或整体垮塌[4];2008年中国南方特大雪灾,造成直接经济损失高达1111亿元[5-6]。许多雪灾事故调查表明,屋面局部雪荷载过大是导致结构损毁的重要原因[7-8]。
风致积雪分布的研究方法包括实地观测[9-10]、理论分析[11]、数值模拟[12-13]和风洞试验研究[14-15]等,一般主要采用数值模拟和风洞试验方法。风吹雪是一种气固两相流,其内在相互作用机理十分复杂。在目前的研究中,无论是数值模拟还是风洞试验,还有许多地方需要改进和完善。如数值模拟中的简化模型与实际情况有较大差别,风洞试验中模型相似准则难以完全满足等等。尽管如此,已有不少研究者通过风洞试验获得了有意义的结果。O′Rourke[14]等人利用水槽及核桃壳粉粒材料进行屋面积雪分布特性研究。Thiis[15]等人对一类通风屋面防渗雪进行风洞试验研究,试验在冷风洞中进行,采用人工生成雪粒,研究了不同屋檐结构对防渗雪效果。Kimbar[16]等人根据雪粒运动方程,分析了风洞试验模型相似参数,并在此基础上对体育场屋盖雪荷载分布进行风洞试验研究。在国内,王卫华[17]等人通过风洞试验研究了不同风向下几种典型屋面的积雪重分布特性,Zhou[18]等人利用风洞试验研究了不同跨度的平屋面积雪重分布特性等。
随着全球气候环境持续恶化,极端天气带来的雪灾事故将越来越多。特别是近几十年来,随着中国城市建设规模的发展壮大,各类用途的大跨度屋面结构不断涌现,大量工业化厂房、库房更是鳞次栉比。因此,寻求在设计阶段充分预测结构的雪荷载分布已变得越来越重要。本文针对几种典型屋面结构,采用风洞试验方法,以细石英砂作为模拟雪粒材料,通过模拟实际降雪和均匀降雪重分布等方法,获得屋面的积雪分布,测量了流场参数,分析了屋面积雪系数分布特性,并与中国荷载规范[19]进行了比较。
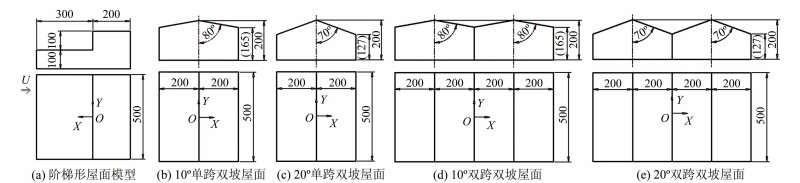
1 风洞试验 1.1 模型及相似参数试验模型包括5种典型屋面结构:1种阶梯形屋面、2种单跨双坡屋面及2种双跨双坡屋面,模型缩尺比为1:40,如图 1所示。
|
| 图 1 试验模型示意图 Fig.1 Scheme of test models |
风吹雪风洞试验的模型相似准则较为复杂。无量纲分析表明,相关模型相似参数多达十几种,不可能全部都能满足。目前大多风洞试验中,主要考虑的重要相似参数包括以下几种[20]:
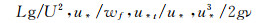 (1)
(1)
式中:g为重力加速度,L为模型特征尺度,U为参考速度,u*为流场摩阻速度,u*t为粒子运动阈值摩阻速度,wf为粒子均匀沉降速度,ν为流体运动粘性系数。除此之外还有一些其他参数,如粒子休止角等。
公式(1)中,第1个为弗劳德数,第2个为速度比,这2个参数由风吹粒子运动方程经无量纲化分析得到;第3个参数也为速度比,是由粒子输运方程经无量纲化分析得到;最后1个参数为流场粗糙长度雷诺数,为满足流动一致性条件,Kind[20]建议其值只要大于下限值30,一般风洞试验中可以满足。
雷诺数参数与弗劳德数是相互矛盾的,使用密度较大的粒子可以满足雷诺数相似而不能满足弗劳德数,反之亦然。许多试验结果表明,满足雷诺数而忽略弗劳德数,试验结果与实测符合最好[20],因此风吹雪风洞试验中一般使用密度较大的粒子。
本试验中雪粒模拟采用100目的石英砂粒子,粒子外形不甚规则,可近似为球形,直径约为0.15mm(±0.05mm),休止角约31°,均匀沉降速度约2.0m/s。模型粒子属性及主要参数如表 1所示。
| 粒子属性及参数 | 石英砂 | 雪粒 |
| 平均直径/mm | 0.15 | 0.1~0.5 |
| 休止角/(°) | 31 | >40 |
| u*t /(m·s-1) | 0.216 | 0.118~0.28 |
| wf/(m·s-1) | 2.0 | 0.31~0.75 |
| u*t3/(2gν) | 30 | 7.0~70.0 |
| u*/u*t | 1.042~1.102 | 0.66~7.93 |
| wf /u* | 8.4~8.89 | 0.327~3.93 |
| wf /u*t | 9.26 | 2.16~5 |
试验在中国空气动力研究与发展中心低速所一座小型下吹式直流风洞中进行,该风洞试验段长3m,截面为0.8m×0.8m的切角正方形,常用试验风速为0~35m/s,图 2为风洞试验段轮廓。

|
| 图 2 风洞试验段轮廓 Fig.2 Picture of wind tunnel test section |
试验前,在整个风洞试验段地板覆盖一层石英砂粒子,厚度约30mm,以模拟来流地面积雪边界条件。石英砂粒子层表面铺盖平整,以避免局部堆积对边界层流场的影响。
屋面积雪系数测量分为降雪模拟试验和均匀重分布试验。降雪模拟试验中,通过模拟降雪获得吹雪气象条件下的屋面初始积雪分布状态;均匀重分布试验则在屋面初始均匀覆盖约20mm厚的粒子层。然后进行吹风试验,获得若干时间内风致屋面积雪重分布特性。模拟降雪试验时风速为2.5m/s,重分布试验时风速为4.6m/s,试验风速以屋面高度为参考。
为实现降雪模拟,在模型前方风洞上壁安装一粒子降落装置,该装置为漏斗形状,漏斗下口处有一阀门,可以控制粒子的下漏速率。
流场测量采用KANOMAX风速计,该仪器为可伸缩热敏探头,不易受气流中细小粒子影响,探头尺寸较细,对流场影响小。
屋面粒子分布深度测量采用数显深度卡尺及辅助工具,测量位置在屋面中心对称面(x轴向),阶梯形屋面只测量低屋面粒子分布。试验前,在模型屋面表面可粘贴一层砂纸,以保证屋面初始粗糙状态。图 3为风洞试验照片。

|
| 图 3 模型风洞试验照片 Fig.3 Model in the test |
积雪边界层流场是完全气动粗糙的,水平平均风速用对数律描述为:
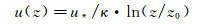 (2)
(2)
式中:κ为冯卡门常数,取0.41;z0为气动粗糙长度。上式可写为:
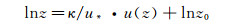 (3)
(3)
利用流场测量得到的风速剖面数据以及最小二乘法,可计算出u*及z0值。
在风洞试验段地板覆盖粒子层后,当风速达到一定值后(即粒子起动阈值风速),粒子开始运动。在风吹雪(或沙)中,粒子发生跃移运动时,跃起的粒子从气流中吸收能量,使周围流速降低,相当于流场有效气动粗糙长度增大了。流场有效气动粗糙长度与摩擦速度平方成正比[21]:
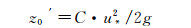 (4)
(4)
式中:g为重力加速度;C为比例系数,可利用流场测量数据拟合得到。
粒子起动阈值风速通过观测得到。当风洞开车速控表读数为6.4时,观测有少量粒子运动,考虑到视觉误差,确定速控表读数6.3时为粒子起动阈值风速,此时对应参考风速为4.4m/s。
1.4 屋面积雪系数中国建筑荷载规范[19]中,屋面雪荷载设计值计算为:
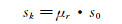 (5)
(5)
式中:sk为雪荷载标准值(kN/m2);μr为屋面积雪分布系数;s0为基本雪压(kN/m2)。中国建筑荷载规范中,基本雪压定义为50年或100年重现期最大雪压,μr为屋面水平投影面积上的雪荷载与s0的比值,实际就是地面基本雪压换算到屋面雪荷载的系数。
本文屋面积雪系数与上述略有差别。在降雪模拟风洞试验中,屋面积雪系数cs定义为屋面粒子沉积厚度h与水平地面平均降落粒子厚度h0的比值,其中h0计算为降落粒子总质量与粒子密度及平均降落面积的比值。在均匀重分布试验中,cs定义与上述类似,只是此时h0取为屋面初始覆盖粒子平均厚度。表 2列出了部分降雪模拟试验中h0值。
| 阶梯屋面 | 10°单跨双坡 | 10°双跨双坡 | |
| Test-1 | 22.0 | 20.8 | 20.5 |
| Test-2 | 23.3 | 22.5 | - |
| Test-3 | 27.6 | 28.7 | - |
由cs及μr定义可看出,二者物理意义是相同的。如果把风洞试验降雪量或初始屋面覆盖深度由原型当地基本雪压换算确定,则二者就完全一致了。
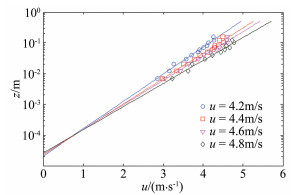
2 结果与分析 2.1 流场测量流场测量取4种风速,分别为风洞速控表读数6.0、6.3、6.5及6.8,对应参考风速分别为4.2、4.4、4.6和4.8m/s。图 4显示了风速剖面测量结果,图中同时给出了拟合曲线。由式(3)计算出流场摩阻速度分别为0.201、0.216、0.225和0.238m/s,即u*t=0.216m/s。由图可看出,在来流u* =0.201m/s时,气动粗糙长度z0最小,随来流风速增大,当u*>*tu时,粒子开始运动,此时有效气动粗糙长度随之增大,表现出风吹雪边界层流场的典型特性。
|
| 图 4 测量的风速剖面 Fig.4 Wind speed profiles |
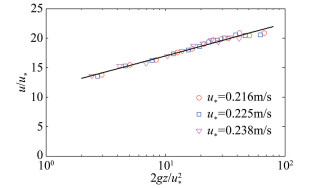
图 5给出了有效气动粗糙长度拟合结果,拟合公式为:
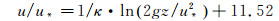 (6)
(6)
|
| 图 5 有效气动粗糙长度拟合 Fig.5 Effective aerodynamic-rough length |
由拟合公式可得式(4)中C=0.0078。
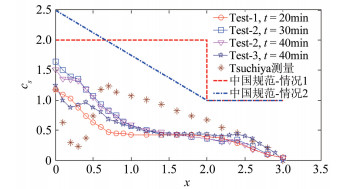
2.2 积雪系数试验结果图中横坐标以阶梯形屋面高差或双坡屋面的斜坡跨距进行无量纲化。图 6显示了阶梯形屋面3次降雪模拟试验结果,图中同时给出了Tsuchiya[9]的3次观测结果平均值及中国荷载规范[19]设计值。由图可见,屋面积雪系数均在中国荷载规范值以内。3次试验结果的变化规律基本相似,主要在高低屋面交界附近(x < 1)差别略大。在x=0处,试验1和3的最大值约1.25,试验2的最大值超过1.5。试验2的2次重分布时间结果变化不大,表明屋面粒子分布接近稳定状态。试验结果与Tsuchiya的观测结果有一定差别,在x=0.3附近,实测积雪系数突然减小至0.2,在x=0.6附近达到最大值,约1.25,而试验结果则平缓下降。这可能是由于一方面存在试验误差,如粒子休止角误差以及模拟参数误差等;另一方面由于观测时间持续较长,受环境变化影响大,如风速、风向、温度以及湿度等的改变。此外,为了防止模型被积雪掩埋,观测模型与地面有一定距离(0.5m),因此屋面积雪不可避免受下洗流动影响,在屋面交界处形成较强的回流涡,造成积雪突然减小。
|
| 图 6 阶梯形屋面积雪系数 Fig.6 Snow coefficients distribution on stepped roof |
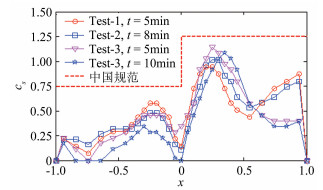
图 7为10°单跨双坡屋面3次降雪模拟试验结果。由图可见,迎风屋面系数较小,在x=-0.2附近最大值约0.5,并随时间发展进一步减小;屋面最大积雪系数在背风屋面靠屋脊后方,最大系数约为1.2,并随时间发展有后移趋势;在背风屋面屋檐附件,试验1和2的结果接近,最大积雪系数值约为0.9,但试验3的结果较小,值约为0.5,这可能是由于模拟降雪速度差别带来的影响。与规范值相比,10°单跨双坡屋面的积雪系数分布形态与规范值基本一致,并在规范值之内。
|
| 图 7 10°单跨双坡屋面积雪系数 Fig.7 Snow coefficients distribution on 10° gable roof |
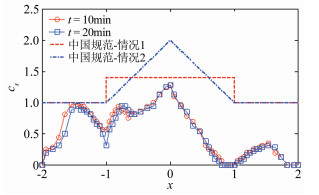
图 8为10°双跨双坡屋面在2个时间段内的降雪模拟试验结果。由图可见,随时间发展,屋面大部分积雪分布变化很小,表明已接近稳定状态;在x < 0时屋面积雪系数相对较大,第1个迎风斜坡屋面(x < -1)最大积雪在屋面中部,积雪系数接近规范值1;在x=0附近由于屋面凹陷,运动粒子大多沉积于此,积雪量最多,最大系数接近规范的情况1。规范的情况2在此处取最大值2,安全系数相对较高,分布形态与试验结果也较吻合。
|
| 图 8 10°双跨双坡屋面积雪系数 Fig.8 Snow coefficients distribution on 10° dual-span gable roof |
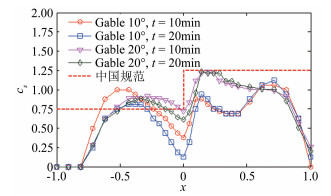
图 9显示了2种单跨双坡屋面均匀重分布试验结果及中国荷载规范值。由图可看出,10°单跨双坡屋面,在迎风屋面前部(x < -0.5)积雪系数较小,而迎风屋面中后部局部系数较大,最大值接近1,超过了中国荷载规范值的0.75,但随着时间发展有所减小。这是由于在开始时,迎风屋面前部粒子受风力侵蚀不断后移,使屋面后部积雪系数初始增加,但随着迁移粒子数减少,屋面后部受风力侵蚀逐渐增大,积雪系数有所减小。背风屋面靠屋檐附近积雪系数值最大,接近规范值的1.25。20°单跨双坡屋面与10°屋面类似,在迎风屋面中后部,最大积雪系数接近1,大于荷载规范值;最大积雪系数在背风屋面的屋脊后方,最大值接近规范的1.25。可以看出,试验的2个时段内背风屋面积雪系数变化较小,表明此处粒子分布已趋于稳定状态。
|
| 图 9 2种单跨双坡屋面积雪系数 Fig.9 Snow coefficients distribution on gable roofs |
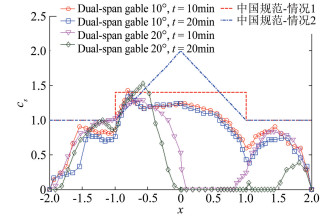
图 10显示了2种双跨双坡屋面均匀重分布试验结果及中国荷载规范值。由图可见,10°双跨双坡屋面的第1个迎风屋面(x < -1)靠近屋脊处,积雪系数相对较大,接近规范值1,但随着时间发展明显减小;屋面最大积雪系数在第1个背风屋面的屋脊后方(-1<x < -0.5),最大系数超过规范值的1.4,而在屋面中间凹陷处积雪系数变化平缓,为1.1左右,这与降雪模拟试验结果有差别;在第2个背风屋面(x>1),最大积雪系数接近规范值1,但随着时间发展明显减小。20°双跨双坡屋面的第1个迎风屋面(x < -1)初始积雪系数相对较大,最大系数接近规范值1,并随着时间发展略有减小;同10°屋面类似,屋面最大积雪系数在第1个背风屋面的屋脊后方(-1 < x < -0.5),初始时积雪系数在规范值以内,约为1.3,但随着时间发展,屋面粒子重分布后,最大积雪系数超过规范值,达到了1.5,并沿流向迅速减小,到第2个迎风屋面(0 < x < 1)处,粒子几乎完全被侵蚀,积雪系数为0;在第2个背风屋面的屋脊后方(1 < x < 1.5),初始屋面积雪系数接近0.9,但随后也很快减小。
|
| 图 10 两种双跨双坡屋面积雪系数 Fig.10 Snow coefficients distribution on dual-span gable roofs |
(1) 在边界层流场测量中,当达到粒子起动的阈值风速后,有效气动粗糙长度随着风速增加而增大,显示出风吹雪边界层流场典型特性。
(2) 阶梯形屋面模拟降雪试验,最大积雪系数在屋面交界处,积雪系数分布形态接近规范的情况1,但与观测值存在误差;单跨双坡屋面的最大积雪系数在背风屋面,但在中国荷载规范值之内,在均匀重分布试验中,2种单跨双坡屋面的迎风屋面积雪系数均超过了中国荷载规范值。
(3) 双跨双坡屋面第1个迎风屋面积雪系数相对较大,但均不大于荷载规范值,并随时间发展略有减小;10°双跨双坡屋面模拟降雪试验,最大系数在屋面中部凹陷位置,与荷载规范的情况2较符合。重分布试验中,2种屋面的最大系数均在第1个背风屋面的屋脊后方,值接近1.5,超过了荷载规范值;20°双跨双坡屋面后半部分屋面积雪系数较小。
(4) 采用本文的风洞试验方法对屋面雪荷载分布预测,可得到屋面最大雪荷载分布位置,从而为结构荷载设计提供参考。
| [1] | Feld J, Carper K. Construction Failure[M]. 2nd ed. New York: John Wiley & Sons , 1987 . |
| [2] | Perski Z, Leijen F van, Hanssen R. Applicability of psinsar for building hazard identification:Study of the 29 January 2006 Katowice Exhibition Hall collapse and the 24 February 2006 Moscow Basmanny Market collapse[C]//Proceedings of the Envisat Symposium 2007, Monteux, Switzerland, 2007. |
| [3] | Lomovtsev E, Grishin A. Market collapse-Moscow's largest-ever man-made disaster[J]. Current Digest of the Russian Press , 2006, 58 (9) : 4–5. |
| [4] | 王元清, 胡宗文, 石永久, 等. 门式刚架轻型房屋钢结构雪灾事故分析与反思[J]. 土木工程学报 , 2009, 42 (3) : 65–70. Wang Y Q, Hu Z W, Shi Y J, et al. Analysis and reflection on snow disaster accidents of steel structures of light-weight buildings with portal frames[J]. China Civil Engineering Journal , 2009, 42 (3) : 65–70. |
| [5] | 蓝声宁, 钟新谷. 湘潭轻型钢结构厂房雪灾受损分析与思考[J]. 土木工程学报 , 2009, 42 (3) : 71–75. Lan S N, Zhong X G. Damage diagnoses and lessons learnt from the failure of light-steel structure by heavy snow in Xiangtan[J]. China Civil Engineering Journal , 2009, 42 (3) : 71–75. |
| [6] | 周昌农. 南方雪灾中轻钢结构房屋灾情调查及原因分析[J]. 城市建设 , 2009, 32 (46) : 286–287. Zhou C N. Damage diagnoses and lessons learnt from the failure of light-steel structure by heavy snow in South China[J]. Chengshi Jianshe Yu Shangye Wangdian , 2009, 32 (46) : 286–287. |
| [7] | 张德海, 南波, 舒铮. 雪灾后某网架破坏分析及加固[J]. 沈阳建筑大学学报(自然科学版) , 2010, 26 (1) : 62–67. Zhang D H, Nan B, Shu Z. Destroying analysis and reinforcement research on space truss structure after snowstorms[J]. Journal of shenyang Jianzhu University(Natural Science) , 2010, 26 (1) : 62–67. |
| [8] | 顾明, 黄友钦, 赵明伟. 风雪共同作用下门式刚架厂房的动力稳定性[J]. 同济大学学报 , 2011, 39 (9) : 1266–1272. Gu M, Huang Y Q, Zhao M W. Dynamic instability of light-weight steel structures with portal frames under wind and snow loads[J]. Journal of Tongji University , 2011, 39 (9) : 1266–1272. |
| [9] | Tsuchiya M, Tomabechi T, Hongoa T, et al. Wind effects on snowdrift on stepped flat roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2002, 90 : 1881–1892. DOI:10.1016/S0167-6105(02)00295-7 |
| [10] | Gordon M, Taylor P A. Measurements of blowing snow, Part I:Particle shape, size distribution, velocity, and number flux at Churchill, Manitoba, Canada[J]. Cold Regions Science and Technology , 2009, 55 (1) : 63–74. DOI:10.1016/j.coldregions.2008.05.001 |
| [11] | O'Rourke M, Degaetano A, Tokarczyk J D. Analytical simulation of snow drift loading[J]. Journal of Structural Engineering , 2005, 131 : 660–667. DOI:10.1061/(ASCE)0733-9445(2005)131:4(660) |
| [12] | Tominaga Y, Okaze T, Mochida A. CFD modeling of snowdrift around a building:An overview of models and evaluation of a new approach[J]. Building and Environment , 2011, 46 (4) : 899–910. DOI:10.1016/j.buildenv.2010.10.020 |
| [13] | 王卫华, 廖海黎, 李明水. 基于时变边界屋面积雪分布数值模拟[J]. 西南交通大学学报 , 2013, 48 (5) : 851–967. Wang W H, Liao H L, Li M S. Numerical simulation of wind-induced roof snow distributions based on time variable boundary[J]. Journal of Southwest Jiao-tong University , 2013, 48 (5) : 851–967. |
| [14] | O'Rourke M, Degaetano A, Tokarczyk J D. Snow drifting transport rates from water flume simulation[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2004, 92 : 1245–1264. DOI:10.1016/j.jweia.2004.08.002 |
| [15] | Thiis T K, Barfoed P, Delpech P, et al. Penetration of snow into roof constructions-Wind tunnel testing of different eave cover designs[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2007, 95 (9-11) : 1476–1485. DOI:10.1016/j.jweia.2007.02.017 |
| [16] | Kimbar G, Flaga A. Wind tunnel tests of snow load redistribution on large span flat roofs[C]. The 13th International Conference on Wind Engineering, Amsterdam, 2011. |
| [17] | 王卫华, 廖海黎, 李明水. 风致屋面积雪分布风洞试验研究[J]. 建筑结构学报 , 2014, 35 (5) : 143–149. Wang W H, Liao H L, Li M S. Wind tunnel test on wind-induced roof snow distribution[J]. Journal of Building Structures , 2014, 35 (5) : 143–149. |
| [18] | Zhou X Y, Kang L Y, Yuan X M, et al. Wind tunnel test of snow redistribution on flat roofs[J]. Cold Regions Science and Technology , 2016, 127 : 49–56. DOI:10.1016/j.coldregions.2016.04.006 |
| [19] | 中华人民共和国建设部. GB 50009-2012建筑结构荷载规范[S].北京:中国建筑工业出版社, 2012. |
| [20] | Kind R J. Snowdrifting:a review of modeling methods[J]. Cold Regions Science and Technology , 1986, 12 (3) : 217–228. DOI:10.1016/0165-232X(86)90036-4 |
| [21] | Beyers J H M, Harms T M. Outdoors modelling of snowdrift at SANAE Ⅳ Research Station, Antarctica[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2003, 91 : 551–569. DOI:10.1016/S0167-6105(02)00409-9 |



