2. 天津大学仁爱学院 数学教学部, 天津 301636 ;
3. 天津市现代工程力学重点实验室, 天津 300350
2. Department of Mechanics, Renai College of Tianjin University, Tianjin 301636, China ;
3. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300350, China
湍流边界层中存在着大尺度的相干结构。通过实验发现,大尺度的相干结构可分为2类:一类存在于湍流边界层的近壁区,与近壁区的猝发现象和湍流产生有关[1],另一类存在于边界层的外边界区[2]。这种湍流边界层外区的超大尺度条纹结构由Marusic et al.[3]发现。Hutchins et al.[4]在湍流边界层的对数律区和尾流区也发现了超大尺度低速和高速条纹结构,该条纹结构流向长度可达到20倍的湍流边界层厚度δ,而条纹最大宽度约为0.5δ。由于这种结构具有很长的流向尺度,且这种结构对湍流边界层能量分布具有重要作用,因此将其称为“Superstructures”。这种超大尺度结构同时也在影响边界层内区的运动。
Adrian[5]认为边界层外区的超大尺度相干结构通常以一组空间关联程度较高的发卡涡(包)的形式存在,发卡涡(包)贯穿整个边界层。Liu et al.[6]指出,超大尺度湍流结构对湍流能量输运起主导作用,占有总湍动能一半以上,而且对湍流边界层外区的雷诺应力的贡献高达2/3至3/4,对湍流的产生和维持有重要贡献[7-11]。Guala et al.[12]通过对管道湍流中的“Superstructures”进行实验研究发现:除了发卡涡包,一定还存在其它原因为对数律区超大尺度结构(>20δ)的形成起重要作用,而且湍流边界层外区超大尺度结构(>20δ)的形成机理与近壁区的大尺度结构的形成机理不同。
子波分析是近些年新发展起来的一种数学方法[13-14],通过信号与一个被称为子波的解析函数进行卷积,将信号在时域与频域空间同时进行分解。姜楠等[15]提出了用子波分析的能量最大准则检测壁湍流相干结构猝发事件的方法。
一维速度信号u(t)在子波函数Wab(t)下的子波分析Wu(a, b)定义为:
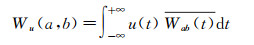 (1)
(1)
其中子波函数族Wab(t)是由子波母函数W(t)经过平移(参数b)和伸缩(参数a)变换而来:
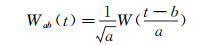 (2)
(2)
子波分析又被称为数学显微镜,其“放大倍数”为参数a,“焦点位置”为参数b,子波母函数W(t)的选择则决定了它的“光学性质”。
根据子波系数Wu(a, b),速度信号u(t)的能量可以分解为
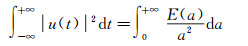 (3)
(3)
各尺度信号所占有能量的总和等于信号的总能量。其中
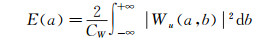 (4)
(4)
姜楠等[15]提出了用子波分析的能量最大准则确定壁湍流相干结构猝发周期时间尺度的方法。在E(a)随尺度a的分布中,每个尺度的湍流脉动速度所占有的湍流脉动动能是不同的,存在着一个峰值,对应能量最大的尺度a*,该尺度就是相干结构猝发周期对应的时间尺度。
本文中用到的小波母函数为二次B-样条函数。
零次B-样条函数就是[0, 1)区间的特征函数,记作:
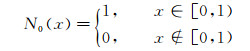 (5)
(5)
m次基数B-样条函数Nm(x)由如下卷积迭代关系定义:
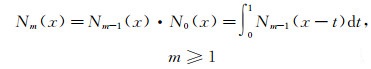 (6)
(6)
显然,Nm(x)是紧支的,其支撑宽度为
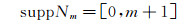
其支撑中心为(m+1)/2, 也是Nm(x)的对称中心。可以得到,二次B-样条函数的数学表达式为:
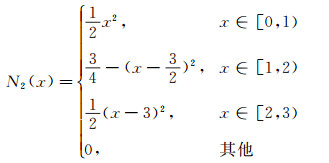 (7)
(7)
由于Nm(x)可以作为一个尺度函数而生成一个多分辨率分析,并且是一类分段光滑又在各段交界处具有一定光滑性的函数。基数B-样条函数Nm(x)具有最小可能的支撑宽度,又便于算法的计算机处理和实时实现。不同子波母函数得到的分析结果有一定的差别,本研究选取的二次B-样条小波和涡结构具有较好的相似性,可以得到较好的结果。
本文采用热线测速实验技术,在风洞中开展湍流边界层外区超大尺度相干结构的实验研究。用子波变换对湍流边界层中不同法向位置的流向和法向瞬时速度信号的时间序列进行多尺度特征分析。目的是希望用子波分析的方法验证边界层的外边界区超大尺度相干结构的存在性,提取湍流边界层外区流向脉动速度和法向脉动速度的分尺度湍动能随尺度和法向位置变化的规律和特征, 提取超大尺度相干结构的喷射和扫掠事件各物理量的条件相位平均波形,分析超大尺度相干结构的相位平均波形与近壁湍流相干结构的相位平均波形之间的差异。
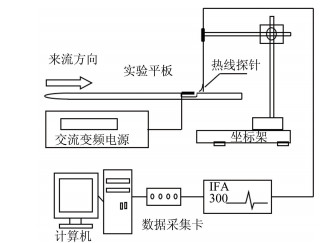
1 实验装置实验在天津大学流体力学实验室的低速回流式木质风洞中进行,实验段长1500mm,横截面为切角的矩形,宽800mm,高600mm。实验段风速在0.5~40m/s之间连续可调,背景湍流度小于0.2%。在风洞中沿中心线竖直放置一块长1700mm、宽600mm、厚15mm的有机玻璃平板,平板前缘为8:1椭圆。以平板前缘为原点建立空间直角坐标系,ox轴正向表示流向,oy轴正向为法向,oz轴正向为展向。在平板前缘x=8cm处安装拌线和砂纸,用来加速转捩并保证在其下游热线探针测量点获得充分发展的湍流边界层(实验装置见图 1)。
|
| 图 1 实验装置示意图 Fig.1 Schematic diagram of the experimental setup |
使用美国TSI公司生产的IFA300恒温式热线风速仪以及TSI-1234-T1.5型双丝边界层热线探针进行测量。这种热线探针的2根热线在空间为互相垂直异面直线布置,热线探针的敏感材料为长1.25mm, 直径4μm的钨丝。热线探针支杆固定在CCTS-1193E型三维自动控制坐标架上。探针在距离平板前缘1090cm处的流向位置测量流向速度分量u和法向速度分量v。实验中选取130个不等间距的法向位置,距离壁面最近的位置4mm,探针移动的步长在近壁区为0.1mm,外区为2mm。
由于在测量速度脉动信号时采样频率要高于湍流的最小时间尺度(耗散尺度),采样时间要长于湍流的最大时间尺度(积分尺度),设定采样频率为100kHz, 低通截止频率为50kHz。每个测量点采集的样本总量为4 194 304个,采样时间为42s。实验中自由来流速度9.59m/s, 边界层的名义厚度为39.88mm,基于边界层名义厚度的雷诺数为Reδ=24 092,基于动量损失厚度的雷诺数为Reθ=2183。
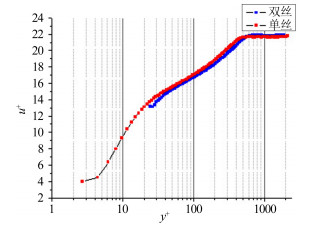
2 实验结果分析图 2为由黏性内尺度单位无量纲化的平板湍流边界层的平均速度剖面。其中u+=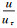
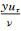
|
| 图 2 平板湍流边界层平均速度剖面 Fig.2 Mean velocity profile of turbulent boundary layer |
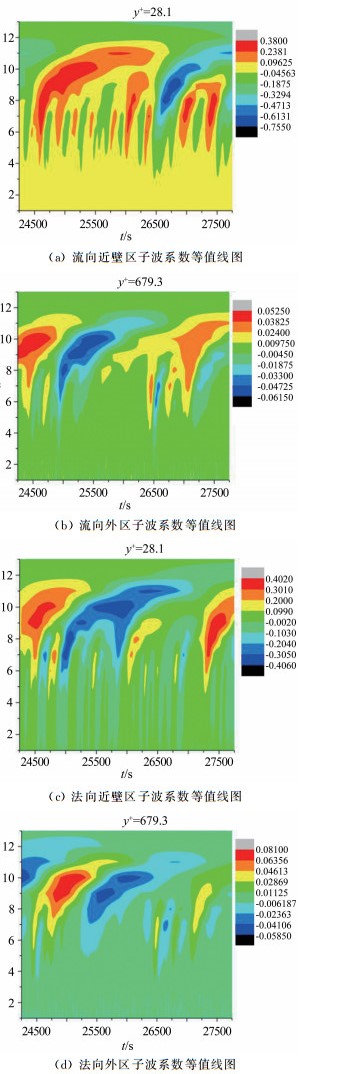
用子波分析对湍流脉动速度信号进行多尺度分解,把湍流流向和法向脉动速度信号分别分解成21个尺度。得到了子波系数在时间和尺度上的等值线图,如图 3所示。不同颜色表示不同子波系数幅值。由图 3可知,不同尺度上存在着一个又一个拟序的湍涡结构,其占有较多的湍流脉动动能。图中分别选取了近壁区y+=28.1和外区y+=679.3这2个不同的法向位置。可以看出,图中分布着不同尺度的涡结构。在近壁区y+=28.1处,流向的能量最大尺度为第9尺度,在外区y+=679.3处,流向的能量最大尺度从第9尺度向第10尺度偏移,说明在外区,相干结构的流向尺度变大。
|
| 图 3 近壁区和外区流向及法向速度信号的子波系数等值线图 Fig.3 Wavelet coefficient contour of streamwise velocity component and normal velocity component in the near-wall and outer region |
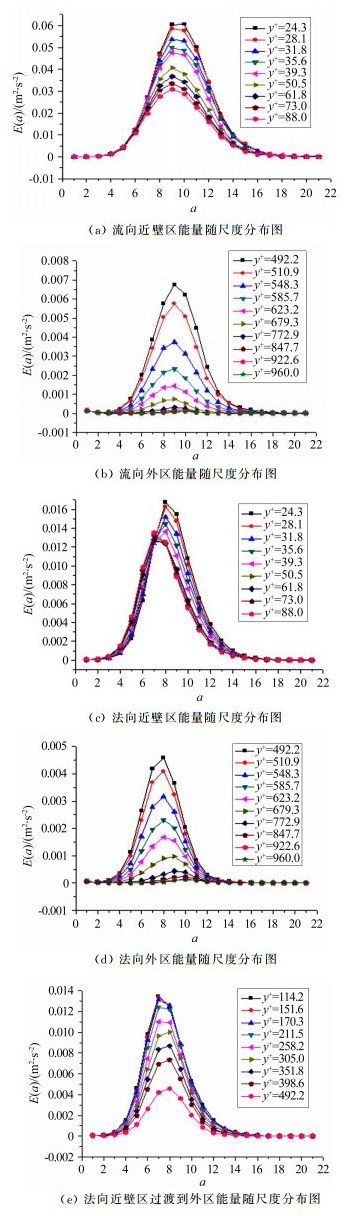
图 4为不同法向位置多尺度流动结构的能量分布线图。图 4(a)为近壁区流向脉动速度能量随尺度分布图;图 4(b)为外区流向脉动速度能量随尺度分布图;图 4(c)为近壁区法向脉动速度能量随尺度分布图;图 4(d)为外区法向脉动速度能量随尺度分布图,图 4(e)为法向脉动速度近壁区过渡到外区能量随尺度分布图。由图 4可以看出,近壁区不同尺度的涡能量随着法向位置远离壁面逐渐减少。表明缓冲层中的相干结构最为活跃,占有特别重要的地位,是湍流产生的主要区域。
|
| 图 4 流法向脉动速度近壁区和外区能量随尺度分布线图 Fig.4 Fluctuating kinetic energy distribution of streamwise velocity and normal velocity component in the near-wall and outer region |
近壁区流向脉动速度的能量最大尺度都在第9尺度,外区y+=679.3处能量最大尺度仍保持在第9尺度,在y+=847.7处能量最大尺度变化到第10尺度。对于法向脉动速度,外区能量最大尺度在y+=679.3处由第8尺度变化到第9尺度,在y+=847.7处能量最大尺度从第9尺度变化到第10尺度。尽管远离壁面区域尺度增大,但是能量却逐渐减弱,这种尺度和能量的变化趋势与Adrian[5]和Ganapathisubramani B.[10]的描述是一致的。
用子波系数模极值法[16-17]提取多尺度相干结构湍涡结构。将流向脉动速度的子波系数是否为负的极小值作为判断是否为喷射事件的标准;子波系数是否为正的极大值作为判断是否为扫掠事件的标准。可以通过测量湍流边界层的近壁区域的脉动速度的时间序列信号,总结出相干结构的基本特征,以此为根据制定相应的判定准则,依据这个判定准则检测相干结构,提取出相干结构的条件相位平均波形。
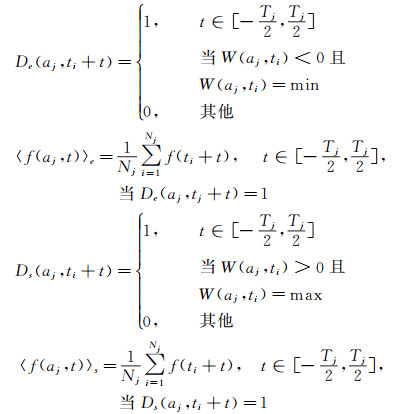
式中:De(aj, ti+t)和Ds(aj, ti+t)分别为喷射和扫掠事件的检测函数;〈f(aj, t)〉e和〈f(aj, t)〉s分别表示喷射和扫掠事件中各物理量对应的条件相位波形,aj为能量最大尺度,E(aj)=maxE(a)。
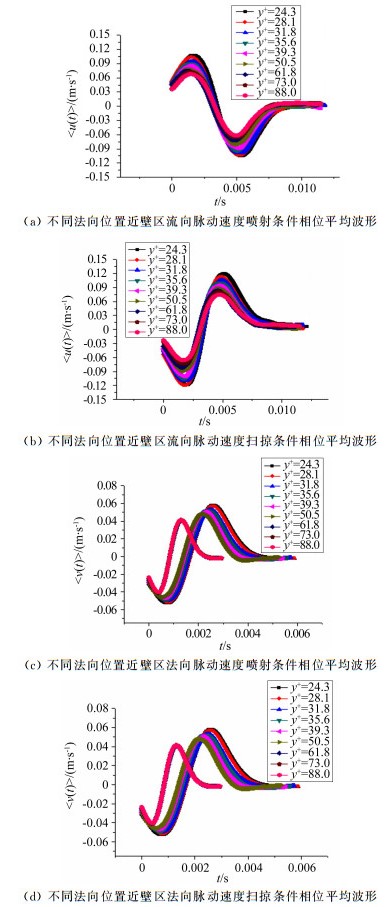
图 5给出了在近壁区不同法向位置的能量最大尺度对应的喷射和扫掠事件相干结构的流向和法向脉动速度的条件相位平均波形。从图 5中可以看出,在不同的法向位置,喷射和扫掠事件的条件相位波形幅值发生了改变。随着法向位置增加,相干结构的流向和法向脉动速度条件相位平均波形的幅值呈减少趋势,表明喷射与扫掠事件的强度减弱。
|
| 图 5 近壁区不同法向位置流向及法向脉动速度喷射扫掠事件的条件相位平均波形 Fig.5 Phase-averaging waveforms of streamwise velocity and normal velocity components in the near-wall region at ejection and sweep events |
湍流脉动喷射和扫掠事件条件相位波形的周期也发生了变化。外区随着能量最大尺度增加,喷射和扫掠事件的时间周期增加。流向脉动速度在外区y+=847.7处能量最大尺度由第9尺度变化到第10尺度,表明喷射和扫掠时间的尺度增加;法向脉动速度在外区y+=679.3和y+=847.7处能量最大尺度由第8尺度变化到第9和第10尺度,相应的喷射和扫掠的时间周期也增加。说明在外区存在着尺度不断增大的相干结构,这些超大尺度相干结构的时间周期比近壁区大尺度结构时间周期要大很多。随着远离壁面,低速度条带区域变宽、变长,这与Del Alamoa et al.[18]的发现是一致的。
在喷射过程中,首先流向速度有一个缓慢的加速过程,然后是一个急剧的减速过程,减速过程非常短暂而强烈,在物理上表现为低速流体抬升远离壁面,低速流体到达测量点后,使当地测量点速度减少。法向脉动速度主要表现为剧烈的加速过程,表明流体向上加速远离壁面。在扫掠过程中,首先是一个缓慢的减速过程,然后是一个急剧的加速过程,加速过程非常短暂而强烈,在物理上表现为高速流体冲向壁面的剧烈下扫,高速流体到达测量点后,使当地测量点速度增加。而在法向是流体向下冲向壁面,法向速度由正变为负。
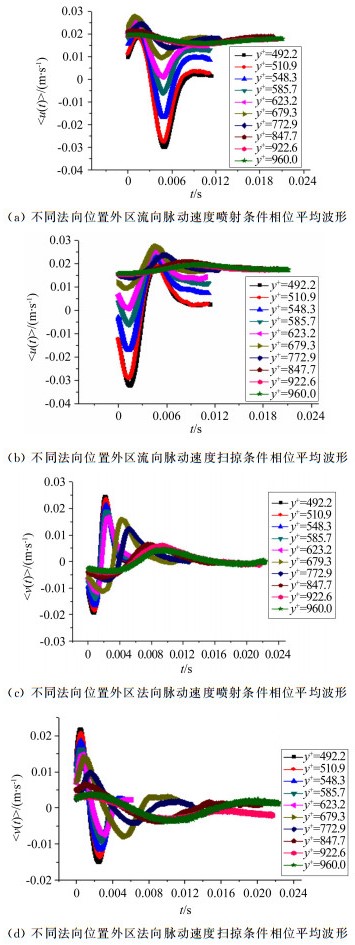
图 6给出了在外区不同法向位置的能量最大尺度对应的喷射和扫掠事件相干结构的流向和法向脉动速度的条件相位平均波形。在外区,喷射事件(见图 6(a))表现出的负的流向脉动速度仍然比较明显,随着远离壁面其负向速度逐渐减弱。而法向脉动速度(见图 6(c))在y+=679.3处时间尺度变大,幅值减小较慢。在y+=847.7处,时间尺度再次变大,幅值没有减小。表明在湍流边界层的外边界,确实存在着超大尺度相干结构的掺混作用。
|
| 图 6 外区不同法向位置流向及法向脉动速度喷射扫掠事件的条件相位平均波形 Fig.6 The phase-averaging waveforms of the streamwise velocity and normal velocity components in the outer region |
在外区,流向脉动速度喷射事件负的流向脉动减少,流向脉动速度转为正值。扫掠事件也是负的流向脉动减少,流向脉动速度转为正值,条件相位波形与近壁区比较发生了改变。法向脉动速度喷射事件也呈现出负的脉动减少、法向脉动速度转为正值的趋势。扫掠事件法向脉动速度转为正值,条件相位波形与近壁区的波形比较发生了改变。这也与外区超大尺度相干结构大量卷吸和掺混边界层外的高速流体有关。Adrian[19]认为,超大尺度相干结构的形成和发卡涡(包)有关,这些发卡涡(包)在流向连贯成一串,使得低动量流体依次通过发卡涡(包)向下传递,这些平行的发卡涡(包)诱导出趋于一致的低动量区域,最终形成了超大尺度运动。在传递过程中,随着流体向下游运动,这些超大尺度结构逐渐远离壁面,与边界层外环境高速流体发生动量交换和掺混,其流向脉动速度逐渐增加,从负值逐渐转为正值,法向脉动速度缓慢地小振幅正负波动。
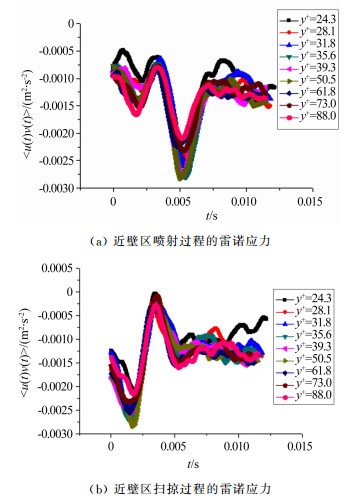
从图 7中可以看出,近壁区喷射和扫掠的过程中,雷诺切应力〈u′v′〉的条件相位波形振幅较大,均为负值,说明流向和法向脉动速度异号特征明显,雷诺切应力〈u′v′〉在象限分布中主要集中在二四象限。由于喷射和扫掠过程中,流向和法向速度分量的条件相位波形总保持几乎相反的相位,因此雷诺应力〈u′v′〉保持为负号且具有很大的幅值。随着法向位置的增加,雷诺应力波形的幅值逐渐减小。
|
| 图 7 近壁区不同法向位置雷诺应力喷射扫掠事件的条件相位平均波形 Fig.7 The phase-averaging waveforms of Reynolds shear stress in the near-wall region at ejection and sweep events |
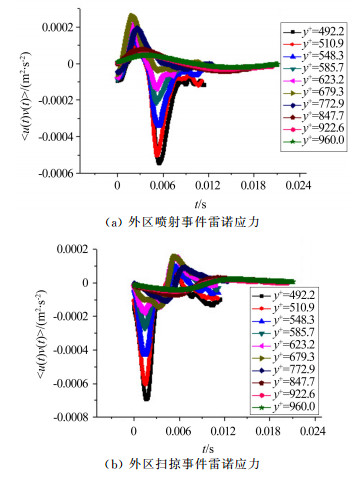
从图 8可以看出,在外区,流向脉动速度在y+=847.7处能量最大尺度由第9尺度变化到第10尺度,雷诺应力〈u′v′ 〉的喷射和扫掠时间尺度相应增加,负的幅值减少,雷诺应力表现为正负交替的波动现象。法向脉动速度在y+=679.3和y+=847.7处能量最大尺度由第8尺度变化到第9和第10尺度,雷诺应力〈u′v′ 〉的喷射和扫掠时间尺度也增加,雷诺应力表现为正负交替的波动现象。
|
| 图 8 外区不同法向位置雷诺应力喷射扫掠事件的条件相位平均波形 Fig.8 The phase-averaging waveforms of Reynolds shear stress in the outer region at ejection and sweep events |
本文用热线风速仪和双丝热线探针精细测量了风洞中湍流边界层不同法向位置流向和法向速度分量的时间序列信号,得出了湍流边界层近壁区及外区不同法向位置的流向和法向脉动速度的子波分尺度能量随尺度分布以及能量最大尺度下喷射和扫掠事件的条件相位平均波形随法向的变化规律,得到以下结论:
(1) 在近壁区由于喷射和扫掠事件导致脉动剧烈,随着法向位置远离壁面,流向和法向脉动速度的能量随尺度分布的强度逐渐减弱,表明随着法向位置远离壁面,湍动能逐渐减少。
(2) 流向脉动速度在近壁区不同法向位置能量最大尺度不变,而到了外区, 能量最大尺度由第9增加到第10尺度;法向脉动速度在外区的能量最大尺度由由第8尺度到第9尺度再到第10尺度逐渐增大。证实了在湍流边界层外区出现了超大尺度的相干结构。
(3) 在不同的法向位置,喷射和扫掠事件的条件相位波形发生了改变。在外区,流向脉动速度喷射和扫掠事件负的脉动减少,正的脉动增多;法向脉动速度喷射和扫掠事件负的脉动减少,正的脉动增多。雷诺应力的条件相位波形发生了改变,雷诺应力负值减少,正值增多,表现为正负交替的波动特征。
| [1] | Robinson S K. Coherent motions in the turbulent boundary layer[J]. Annu Rev Fluid Mech , 1991, 23 : 601–639. DOI:10.1146/annurev.fl.23.010191.003125 |
| [2] | Falco R E. Coherent motions in the outer region of turbulent boundary layers[J]. Phys Fluids , 1977, 20 : S124–S132. DOI:10.1063/1.861721 |
| [3] | Hutchins N, Marusic I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers[J]. J Fluid Mech , 2007, 579 : 1–28. DOI:10.1017/S0022112006003946 |
| [4] | Hutchins N, Hambleton W T, Marusic I. Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers[J]. J Fluid Mech , 2005, 541 : 21–54. DOI:10.1017/S0022112005005872 |
| [5] | Adrian R J, Meinhart C D, Tomkins C D. Vortex organization in the outer region of the turbulent boundary layer[J]. J Fluid Mech , 2000, 422 : 1–54. DOI:10.1017/S0022112000001580 |
| [6] | Liu Z, Adrian R J, Hanratty T J. Large-scale modes of turbulent channel flow:transport and structure[J]. J Fluid Mech , 2001, 448 : 53–80. |
| [7] | Kim K C, Adrian R J. Very large-scale motion in the outer layer[J]. Phys Fluids , 1999, 11 (2) : 417–422. DOI:10.1063/1.869889 |
| [8] | Christensen K T, Adrian R J. Statistical evidence of hairpin vortex packets in wall turbulence[J]. J Fluid Mech , 2001, 431 : 433–443. DOI:10.1017/S0022112001003512 |
| [9] | Natrajan V K, Christensen K T. The role of coherent structures in subgrid-scale energy transfer within the log layer of wall turbulence[J]. Phys Fluids , 2006, 18 (6) : 065104. DOI:10.1063/1.2206811 |
| [10] | Ganapathisubramani B, Hutchins N, Hambleton W T, et al. Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations[J]. J Fluid Mech , 2005, 524 : 57–80. DOI:10.1017/S0022112004002277 |
| [11] | Wu Y, Christensen K T. Population trends of spanwise vortices in wall turbulence[J]. J Fluid Mech , 2006, 568 : 55–76. DOI:10.1017/S002211200600259X |
| [12] | Guala M, Hommema S E, Adrian R J. Large-scale and very-large-scale motions in turbulent pipe flow[J]. J Fluid Mech , 2006, 554 : 521–542. DOI:10.1017/S0022112006008871 |
| [13] | Farge M. Wavelet transforms and their applications to turbulence[J]. Annu Rev Fluid Mech , 1992, 24 : 395–457. DOI:10.1146/annurev.fl.24.010192.002143 |
| [14] | Marie Farge, Nicholas Kevlahan, Valerie Perrier. Wavelets and turbulence[J]. Proceedings of the IEEE , 1996, 84 (4) : 639–669. DOI:10.1109/5.488705 |
| [15] | 姜楠, 王振东, 舒玮. 子波分析辨识壁湍流猝发事件的能量最大准则[J]. 力学学报 , 1997, 29 (4) : 406–412. Jiang N, Wang Z D, Shu W. The maximum energy criterion for identifying burst events in wall turbulence using wavelet analysis[J]. Chinese Journal of Theoretical and Applied Mechanics , 1997, 29 (4) : 406–412. |
| [16] | Liu J H, Jiang N, Wang Z D, et al. Multi-scale coherent structures in turbulent boundary layer detected by locally averaged velocity structure functions[J]. Applied Mathematics and Mechanics , 2005, 26 (4) : 456–464. |
| [17] | Zheng X B, Jiang N. Experimental study on spectrum and multi-scale nature of wall pressure and velocity in turbulent boundary layer[J]. Chinese Physics B , 2015, 24 (6) : 064702. DOI:10.1088/1674-1056/24/6/064702 |
| [18] | Del Alamo J C, Jimenez J. Spectra of the very large anisotropic scales in turbulent channels[J]. Phys Fluids , 2003, 15 (6) : L41–44. DOI:10.1063/1.1570830 |
| [19] | Zhou J, Adrian R J, Balachandar S, et al. Mechanism for generating coherent packets of hairpin vortices in channel flow[J]. J Fluid Mech , 1999, 387 : 353–396. DOI:10.1017/S002211209900467X |



