高超声速风洞喷管设计目前普遍采用无粘型面加边界层修正的直接设计方法,相比于优化设计[1-3],该方法原理简单计算便捷,在广泛应用中取得了成功。然而在实践中有时也发现一个问题,即风洞运行的实际流场与喷管设计流场存在差异。该问题的产生因素有很多,包括来流非均匀非稳态、非平衡膨胀、边界层转捩、热化学非平衡、气体组分冷凝、加工和组装精度、喷管内表面侵蚀和型面的力热变型等,但喷管的无粘型面设计则是其中最重要的一个方面,因而分析其差异应首先确认喷管无粘型面设计方面的问题。
无粘型面直接设计方法根据原理可分为3类:基于预设初始膨胀段型面的方法[4];基于泉流(或源流)假设的方法(如Foelsch[5]方法、Cresci[6]方法和Sivells[7-8]方法)和基于超声速区预设轴线马赫数分布的方法(如ASN[9]方法)。研究表明,第2类基于泉流假设的方法(特别是Sivells方法)在选择合适的类方法设计的喷管长度较长,调整不易。第1类和第3类方法均需计算完整的超声速区特征线网,区别在于第1类方法依据预设的初始膨胀段型面确定轴线上核心区的马赫数分布,而第3类方法则根据预设的轴线马赫数分布反求喷管型面。但在喉道附近利用特征线法从预设的喷管型面计算流场,相比利用轴线上给定的速度分布反算能产生该预设速度分布的型面要困难。
超声速区轴线马赫数分布的预设方法,最简单的是采用多项式分布描述,比如采用三次多项式[10]或五次多项式。多项式系数根据超声速区起点和终点的马赫数及其一阶和二阶导数条件确定,并可以通过附加项调整三次多项式,使得内部分布可调。但随着马赫数升高或者喷管长度增加,采用三次或五次多项式分布会使得轴线存在大于出口马赫数的区域,导致轴线马赫数分布出现问题。易仕和等人考虑采用Bezier曲线[9, 11]和B样条曲线[9, 12]的轴线上速度分布方法直接避免该问题,而Tajfar等人[10]考虑利用泉流面积比和马赫数的关系,首先由三次或五次多项式描述面积比分布,然后根据面积比反算马赫数分布。采用了面积比的多项式分布后,轴线马赫数不会超过设计出口马赫数,但仍可能产生分布不合理的现象,特别是在起点附近可能马赫数增长过快,进而导致计算特征线网时特征线相交。为此本文在Tajfar方法的基础上做出改进,解决局部速度分布不合理的问题。
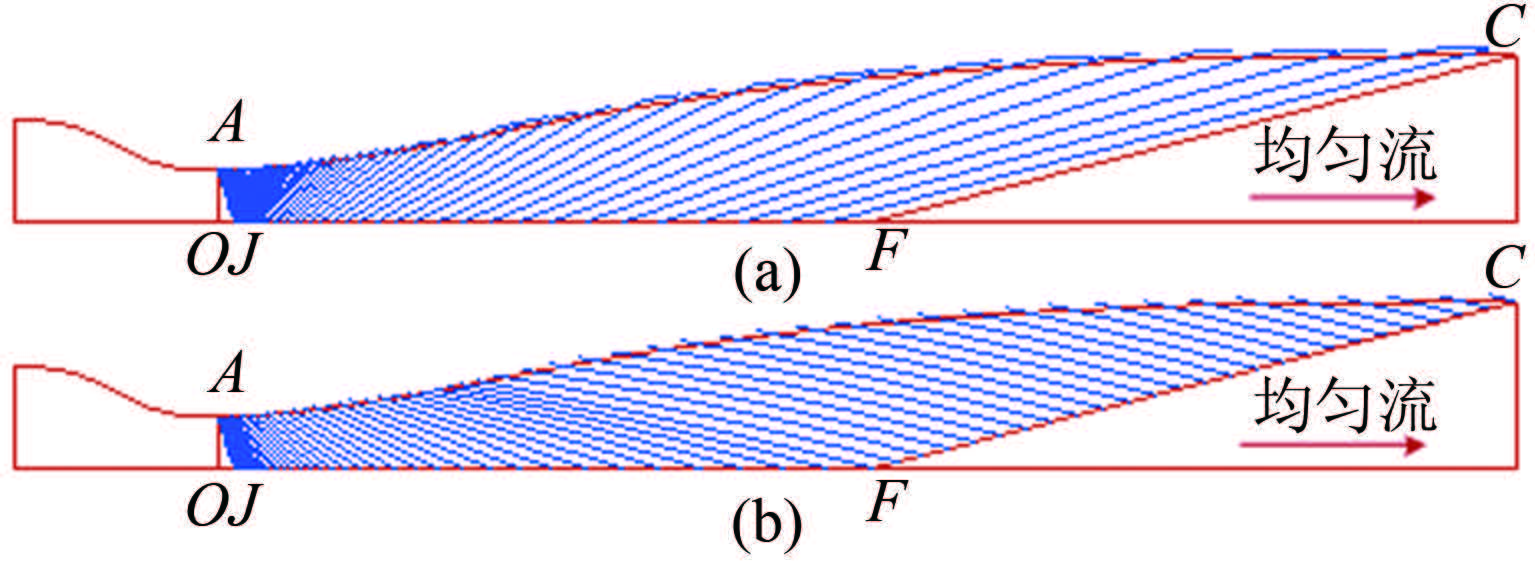
喷管直接设计方法应用的基本技术是特征线网计算[4, 13-14]和型面点确定技术。型面点的确定可采用流函数法和流量积分法,本文采用Moger和Ramsay[14]提出的抛物拟合的流量积分法。特征线网计算过程中分从前往后和从后往前2种推进方法,在已知边界情况下可利用左行特征线一条一条的往上游推进或利用右行特征线往下游推进(见图 1),本文采用向下游推进的方法。为研究无粘型面设计和特征线网质量的影响因素,本文将对设计喷管的特征线网进行Delaunay三角化[15],并与数值模拟流场结果进行比较分析。
|
| 图 1特征线推进方法 (a)往上游推进 (b)往下游推进 Fig.1Characteristic marching method (a) march upstream (b) march downstream |
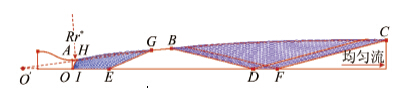
轴线上的马赫数分布预设可分为分段预设和统一预设2种方法。Sivells方法在本文作者看来,可以理解为是一种分段预设方法。该方法将轴线分成3个部分,从声速点I到点E是泉流开始的区域,速度分布用四次多项式描述,从E点到D点为泉流区,从D点到F点是均匀流开始的区域,马赫数分布用一个五次多项式描述(见图 2)。轴线分成3段,但结合起来就是一种轴线马赫数分布,若给出喉部的一条初始线AJ(通过喉部跨声速近似解[16-17]确定一条初值线并由MOC求得),再结合出口马赫线FC,即可通过MOC计算喷管扩张段完整特征线网(见图 3)进而确定喷管型面,而无需分段计算特征线网(见图 2)。
|
| 图 2Sivells方法确定喷管型面 Fig.2Sivells method to determine the nozzle contour |

|
| 图 3基于Sivells方法预设轴线马赫数分布的特征线网 Fig.3Characteristic network based on the Sivells’ axial Mach number distribution |
轴线上马赫数分布的统一预设可采用多种方法,比如三次多项式、五次多项式、Bezier曲线、B样条曲线,以及面积比的三次多项式等。预设马赫数需满足条件:J点:Ma(xJ)=MaJ,Ma′(xJ)=Ma′J,Ma″(xJ)=Ma''J,F点:Ma(xF)=MaF,Ma′(xF)=0,Ma″(xF)=0。J点信息在已知喉道曲率半径和转折角情况下通过跨声速近似解或CFD解获得,一阶和二阶导数通过差分方法计算。而F点的位置为:
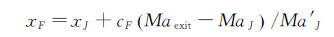 (1)
(1)
其中cF≥1为调整喷管长度的系数。
三次多项式分布为:
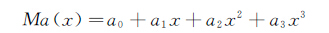 (2)
(2)
改进的三次多项式分布可通过a4系数进行内部微调:
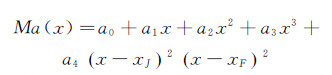 (3)
(3)
五次多项式分布为:
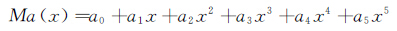 (4)
(4)
Bezier曲线和B样条曲线分布公式相对复杂,2种曲线的定义、构造和插值可参考文献[18-19]。这里给出p次B样条曲线的应用。对于轴线上马赫数分布问题,B样条曲线是u(u∈[0,1])的函数,由n+1个p阶基函数构成,基函数需要m=n+p+1个节点构造,节点构成的节点矢量ui(i=0,…,m)采用平均分布,控制点Pi(i=0,…,n)为(x,Ma)坐标,B样条曲线描述的马赫数分布由参数u的方程表示:
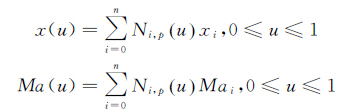 (5)
(5)
控制点P0为:(x0,Ma0)=(xJ,MaJ)
控制点P1由起点的一阶导数确定:
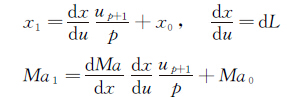 (6)
(6)
其中dL是可调参数,常取控制点构成的总弦长,当得到的控制点不合理时,可适当调整其大小。控制点P2由起点的二阶导数确定:
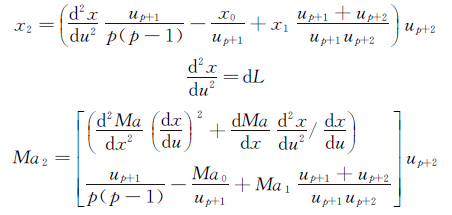 (7)
(7)
控制点Pn为:(xn,Man)=(xF,Maexit)
控制点Pn-1由终点的一阶导数确定:
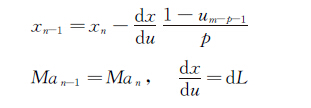 (8)
(8)
控制点Pn-2由终点的二阶导数确定:
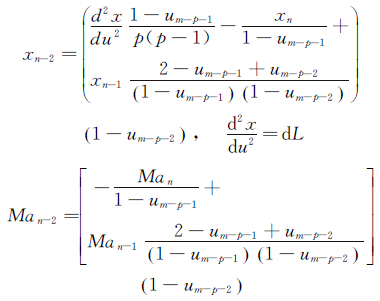 (9)
(9)
上述6个控制点已经足够构成B样条曲线的马赫数分布,若仍然需要进行内部微调,可以在控制点2~(n-2)之间增加控制点。
为解决轴线上局部区域马赫数可能大于出口马赫数的问题,Tajfar等人考虑利用泉流区面积比和马赫数的关系,首先由三次多项式描述面积比分布,然后根据面积比反算马赫数分布。泉流面积比Ar与马赫数的关系为:
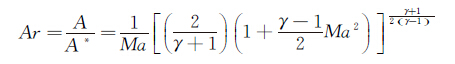 (10)
(10)
而面积比由三次多项式表示
 (11)
(11)
其中J点面积及其导数信息可以由(10)式及其导数与J点马赫数及其导数计算得到:
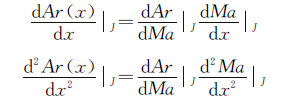 (12)
(12)
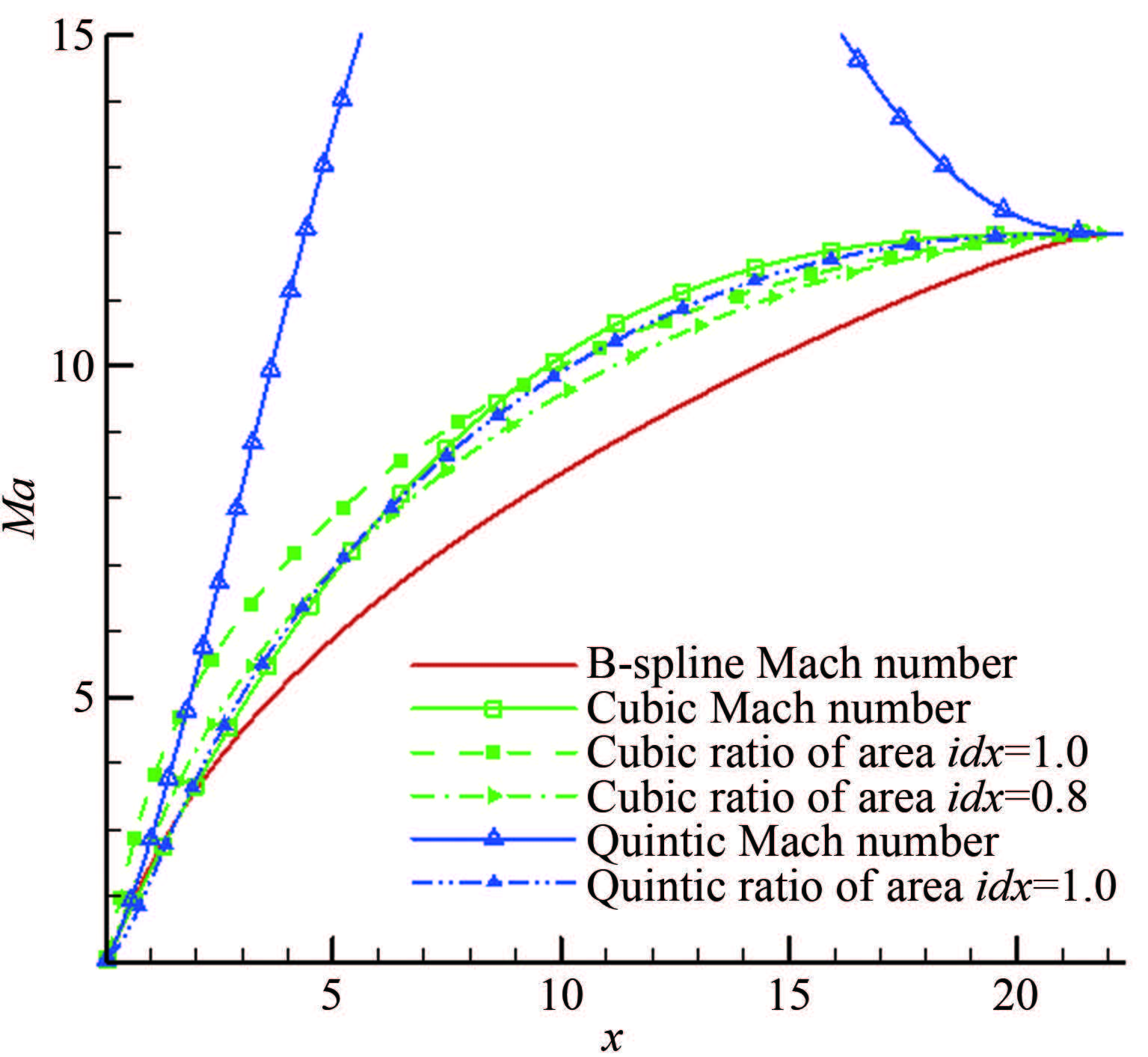
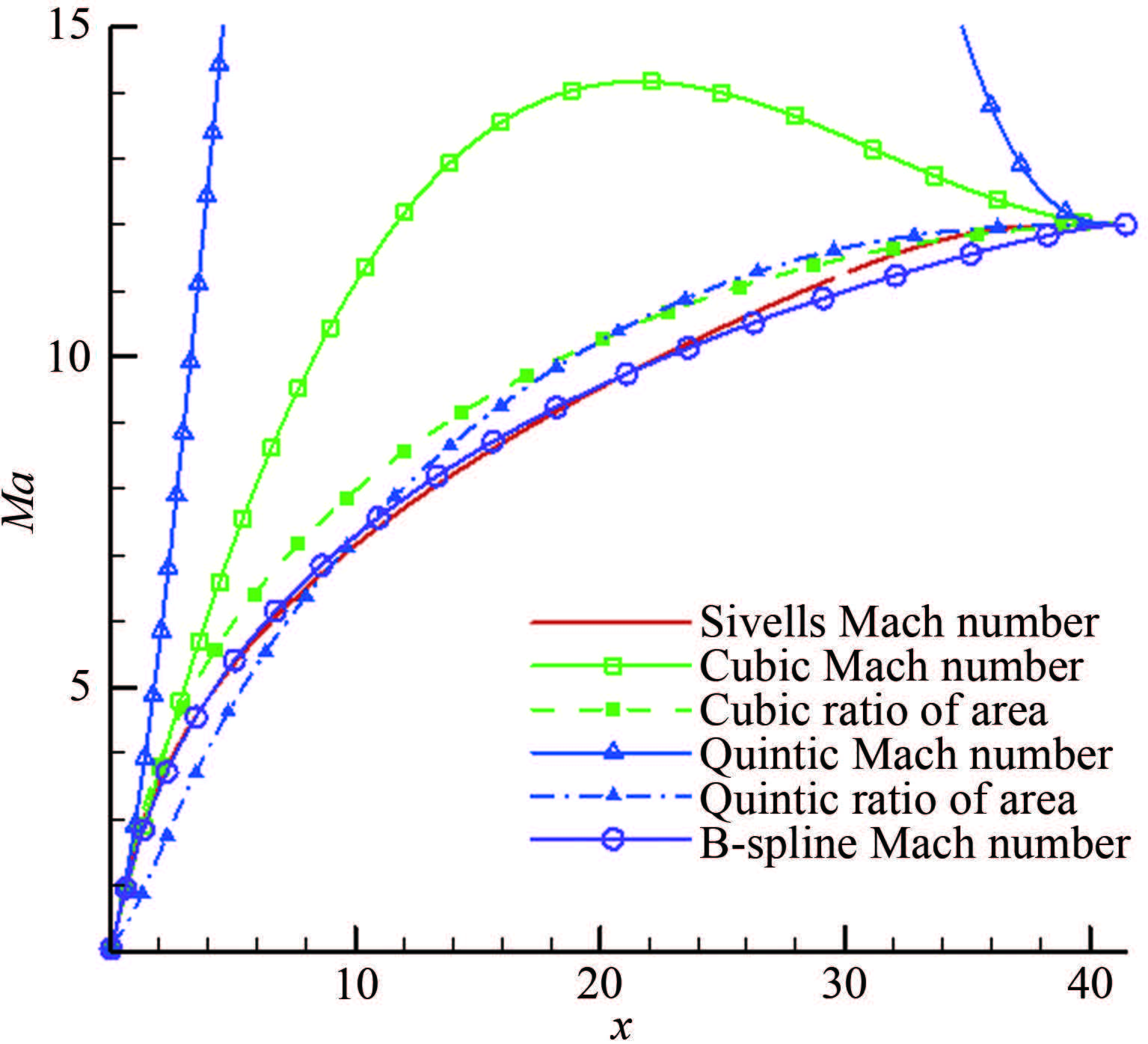
图 4~5给出了喷管出口马赫数为12,cF取3.0和5.57时,不同预设方法的马赫数分布比较。喷管喉道曲率半径比等设计参数与Sivells方法选取的参数一致。cF=5.57是喷管长度与Sivells喷管长度一致时的取值。
|
| 图 4不同预设方法的轴线马赫数分布(cF=3.0时) Fig.4Axial Mach number of different presetting methods with cF=3.0 |
|
| 图 5不同预设方法的轴线马赫数分布(cF=5.57时) Fig.5Axial Mach number of different presetting methods with cF=5.57 |
随着cF取值增大,喷管长度增加,三次或五次多项式描述的马赫数会明显超过出口马赫数。图 6表明采用三次多项式分布,cF=4.0,轴线上特征点采用双曲加密(两端系数分别为0.99和0.50)时特征线出现相交。实践表明:当轴线上的马赫数略超过出口马赫数时,特征线并不一定相交,但随着超出程度增大,特征线出现相交。
|
| 图 6轴线上马赫数大于出口马赫数时的特征线相交 Fig.6Characteristic intersection when Mach number on axis larger then Maexit |
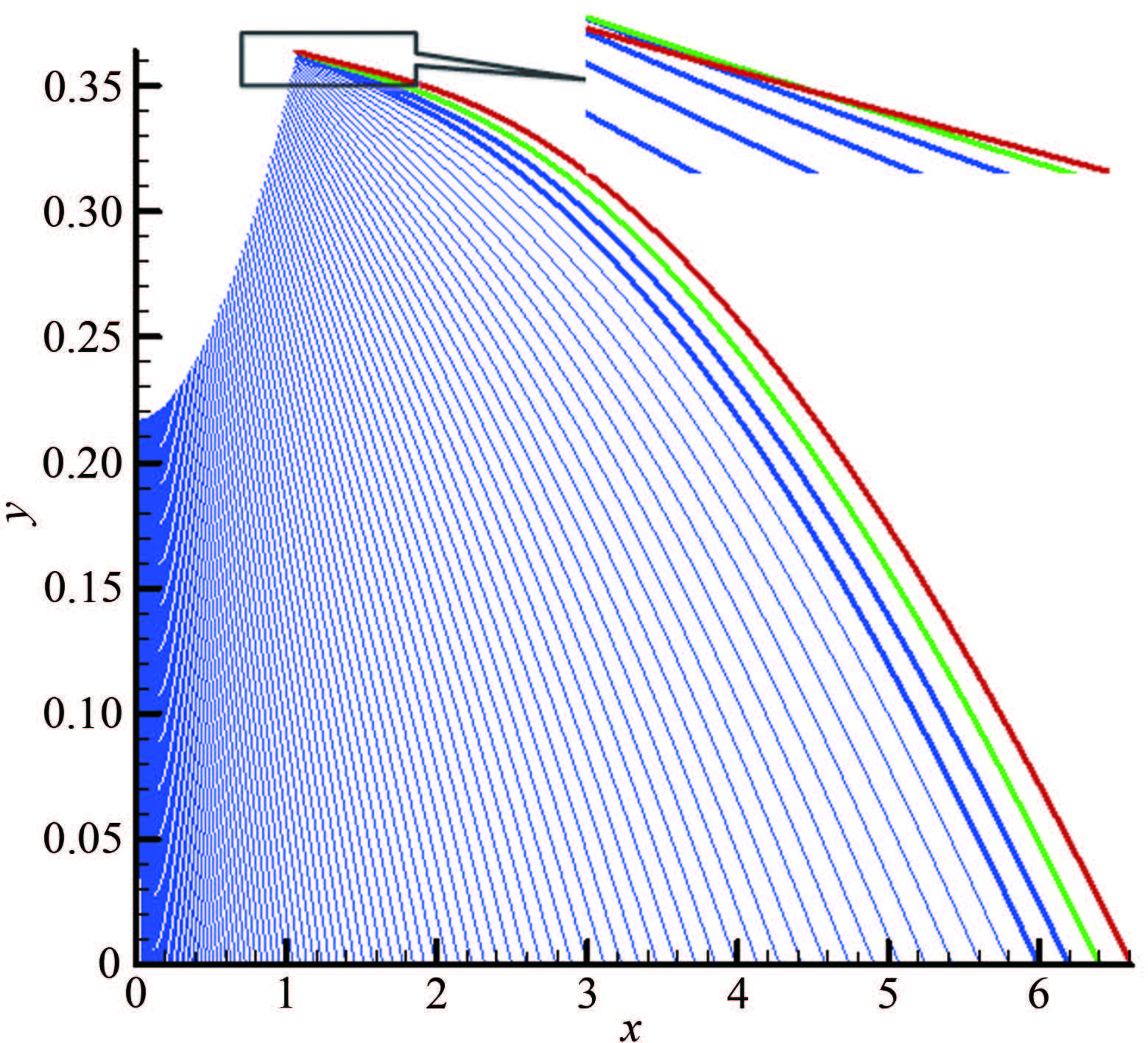
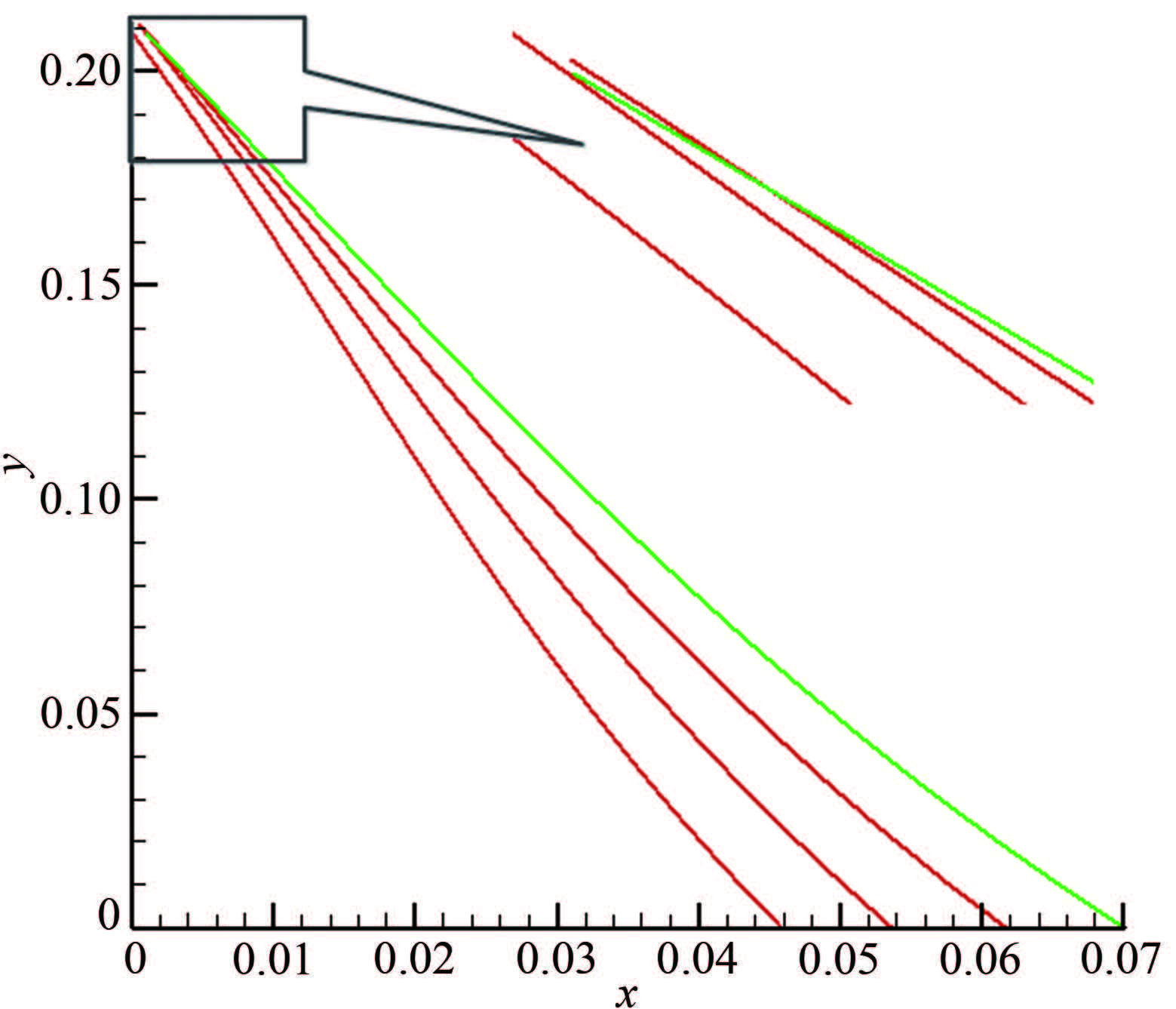
事实上,采用面积比的三次分布方法后,轴线马赫数不会超过出口马赫数,但仍可能存在不合理的地方,特别是当cF较小时,采用面积比的三次多项式分布,其起点J附近马赫数增长明显快过B样条曲线和Sivells方法的结果(见图 4),而因为马赫数增长过快,很可能导致计算特征线网时特征线相交。图 7给出了面积比三次多项式分布,cF=2.9,轴线点加密同图 6时,起点J附近特征线网相交的情况。
|
| 图 7马赫数增长过快导致的特征线相交(J点附近) Fig.7Characteristic intersection caused by too fast Mach number increase (near J point) |
为了避免在起点附近出现速度增长过快问题,本文在(10)式的基础上做出改进,增加一个指数系数idx使起点附近马赫数的增长速度可调,如式(13)所示:
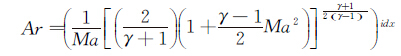 (13)
(13)
尽管式中增加了一个系数但利用相关函数控制马赫数分布的本质没有变。当idx取1.0时,就是原面积比的方法,而当需要减小马赫数增长速度时,仅需调整系数idx取值小于1.0,反之亦然。图 4表明idx系数为0.8的面积比预设方法在起点附近马赫数增长速度明显低于idx取1.0的情况。总的来说,面积比方法的改进,既满足了超声速区起点和终点马赫数及其导数的连续,又保证了轴线上的马赫数不超过出口马赫数,避免过膨胀导致的冷凝问题,也保证了超声速区起点和终点附近的马赫数增长的合理性。表 1总结了几种轴线马赫数分布方法的特点,表明改进的面积比方法可以适用于任意长度喷管设计,且比采用B样条曲线计算量小,也更易于理解。
| 分布方法 | 计算量 | 可调参数 | 适用范围 |
| 三次多项式 | 低 | 无 | 短喷管 |
| 改进的三次多项式 | 低 | a4,内部微调 | 短喷管 |
| 五次多项式 | 低 | 无 | 短喷管 |
| 面积比的多项式 | 中 | 无 | 长喷管 |
| 改进的面积比的多项式 | 中 | idx,控制起点终点的马赫数增长 | 任意 |
| Bezier或B样条曲线 | 高 | dL,控制起点终点的曲线导数进而控制马赫数 | 任意 |
轴线上特征点的分布可采用指数函数加密[19]:
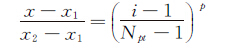 (14)
(14)
其中p=1时为平均分布,p>1时为指数加密,Npt为特征点总数,x1,x2为起点终点坐标。也可以采用双曲函数加密:
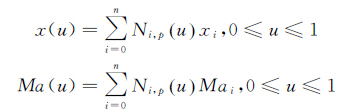 (15)
(15)
其中b1,b2为加密参数,b1控制首端,b2控制未端,取值范围[0~1),取值越接近1,加密程度越高。
上述2种加密方式,点的分布调整相对单调。文本提出一种多点控制的方法以实现更大的自由度。首先任意给定需要加密的位置(即控制点位置),并根据控制参数(统一给单侧双曲加密参数,如(15)式中的b1并取b2=0)统一确定各位置的网格间距(该间距为第一个网格的间距),每个控制段(2个相邻控制点之间)的各网格间距采用线性分布,则各控制段的所有网格确定,进而确定各段的网格数。各控制段的网格数在总网格数的比例乘以实际的网格数就是最终各段的实际网格数。然后根据网格间距线性分布规律,自动调整各段两端的网格间距从而确定所有布点。
考虑在[0,1)线段上布点,特征点数为151,实际网格数为150,考虑控制点(0,0.05,0.15,0.6,1.0),控制参数(0.9999,0.99,0.95,0.90,0.1),计算过程如下:
(1) 由式(15)确定(式中x1=0,x2=1,b2=0)各控制点网格间距为:(0.6779×10-5,0.3585×10-3,0.125910-2,0.207610-2,0.6578×10-2)
(2) 各控制段的末端网格间距与首端比值rdi为:(52.8787,3.51314,1.64866,3.16826)
(3) 由(16)式计算各段应布置网格数为:(273,123,269,92)
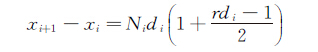 (16)
(16)
其中i为第i个控制点,Ni为控制点i~i+1段网格数,di为i点的网格间距,rdi=di+1/di。
(4) 确定各段实际布置点数为:(54,24,53,19)
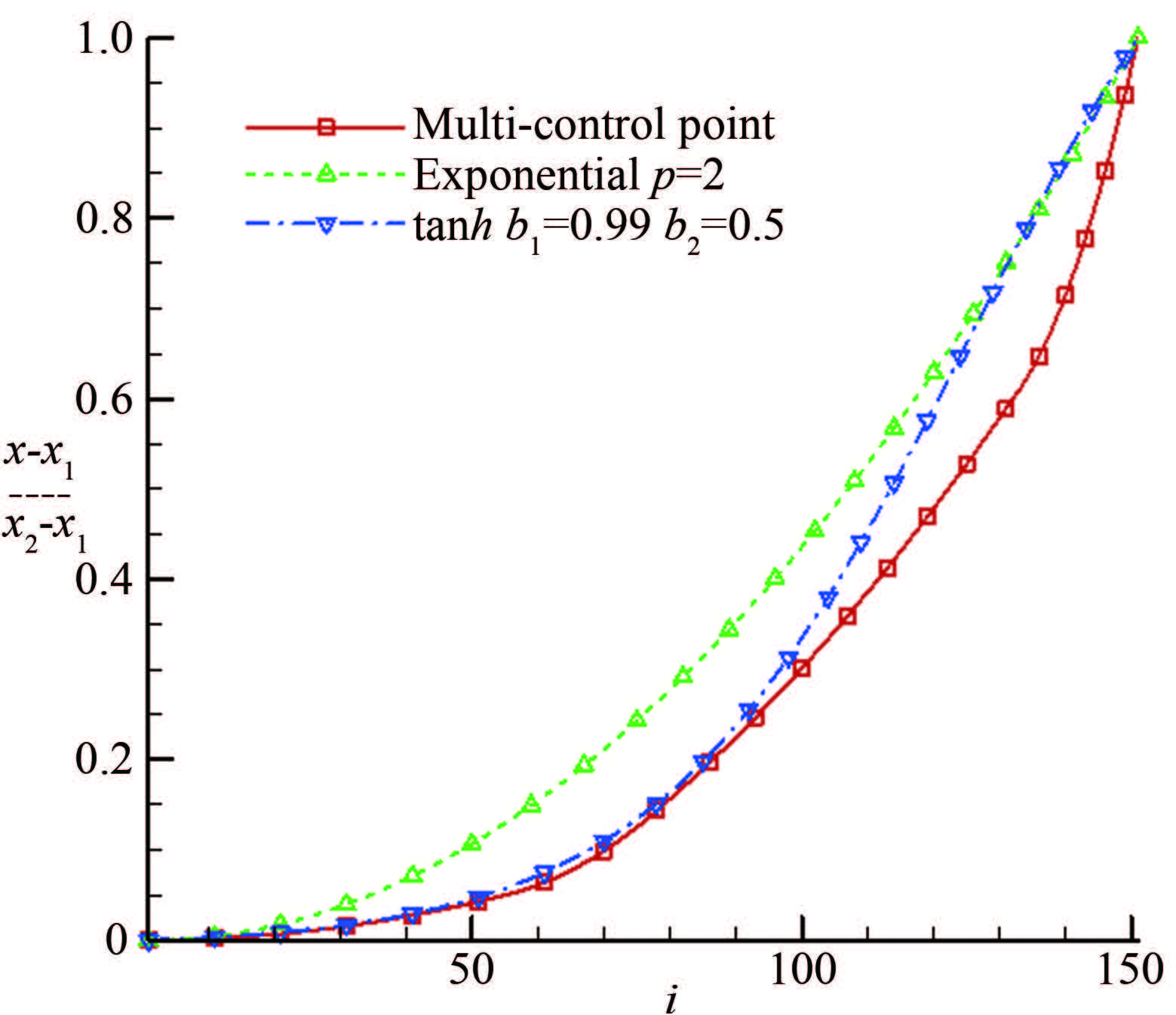
(5) 由(16)式确定各段实际的首端网格间距为:(0.3437×10-4,0.184610-2,0.641110-2,0.1010×10-1),末端网格间距和首端网格间距的比值不变,进而根据网格间距线性分布确定所有的点的位置。图 8给出了上述3种不同布点方法的结果。
|
| 图 8不同方法的布点比较 Fig.8Point distribution of different methods |
喷管无粘型面的设计实践表明,随着喷管设计出口马赫数的提高,喷管长度增加,误差会更为显著,因此本文考虑设计马赫12喷管,对无粘型面设计及其影响因素进行分析。
2.1 轴线马赫数分布的影响喷管设计考虑特征点数:取AJ段81,JF段181,FC段251,转折角12°,喉道曲率半径比12。首先考虑与Sivells喷管长度一致(cF取5.57),比较4种马赫数分布:(Case1) Sivells分布,dMa为D点马赫数与D点最小可取值之差和F点马赫数与该最小值之差的比值,取0.8;(Case2) 面积比的三次多项式分布;(Case3) 面积比的五次多项式分布;(Case4) B样条分布,dL取0.2·(xF-xJ)。
然后考虑稍短的喷管(cF取3.0),比较4种马赫数分布的结果:(Case5) 马赫数的三次多项式;(Case6) 面积比的三次多项式,idx=0.8;(Case7) 面积比的五次多项式;(Case8) B样条分布,dL取0.3·(xF-xJ)。
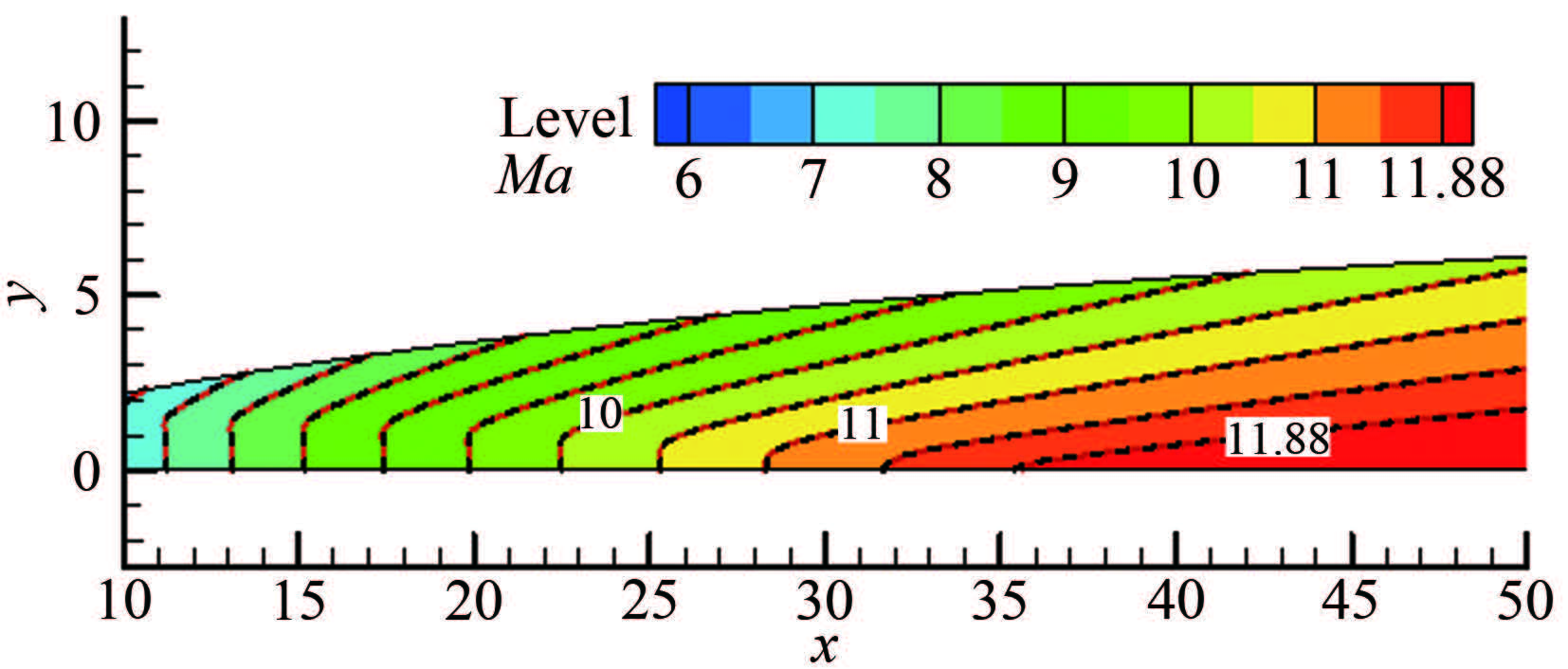
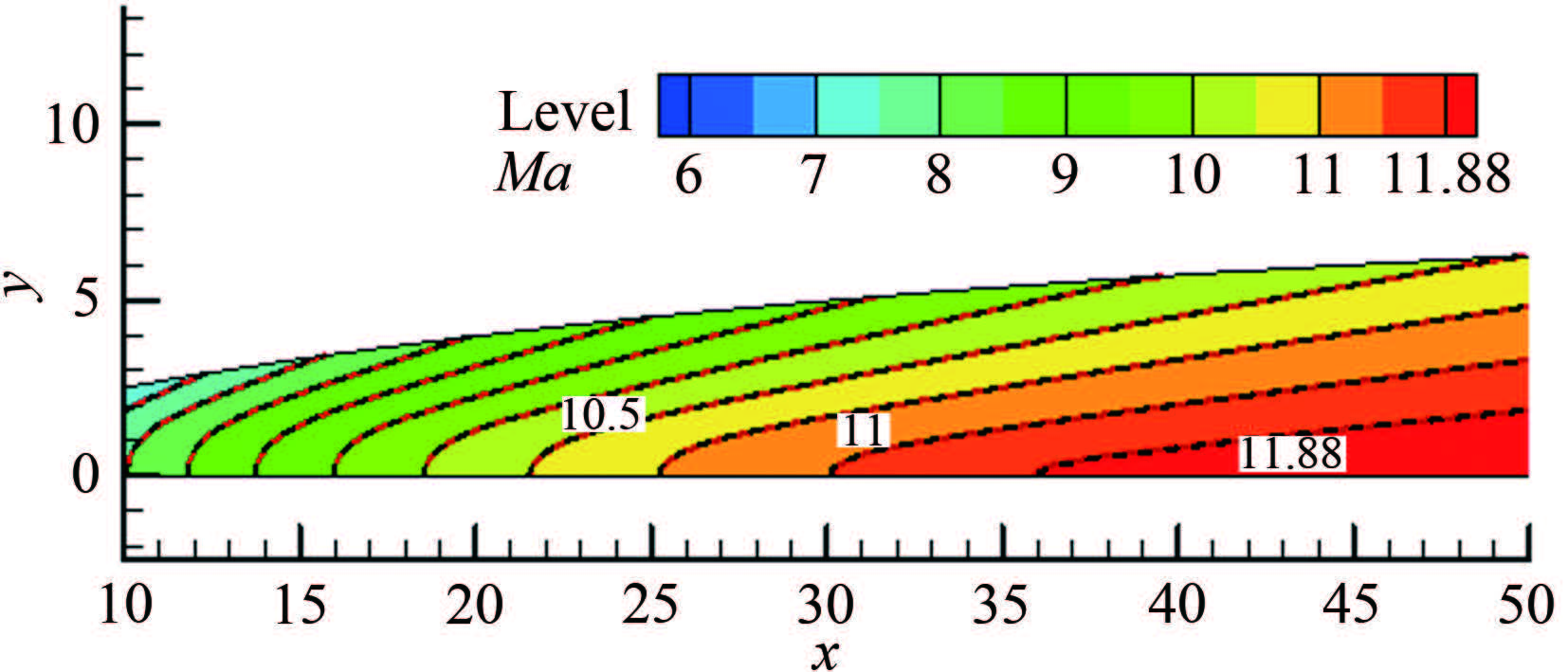
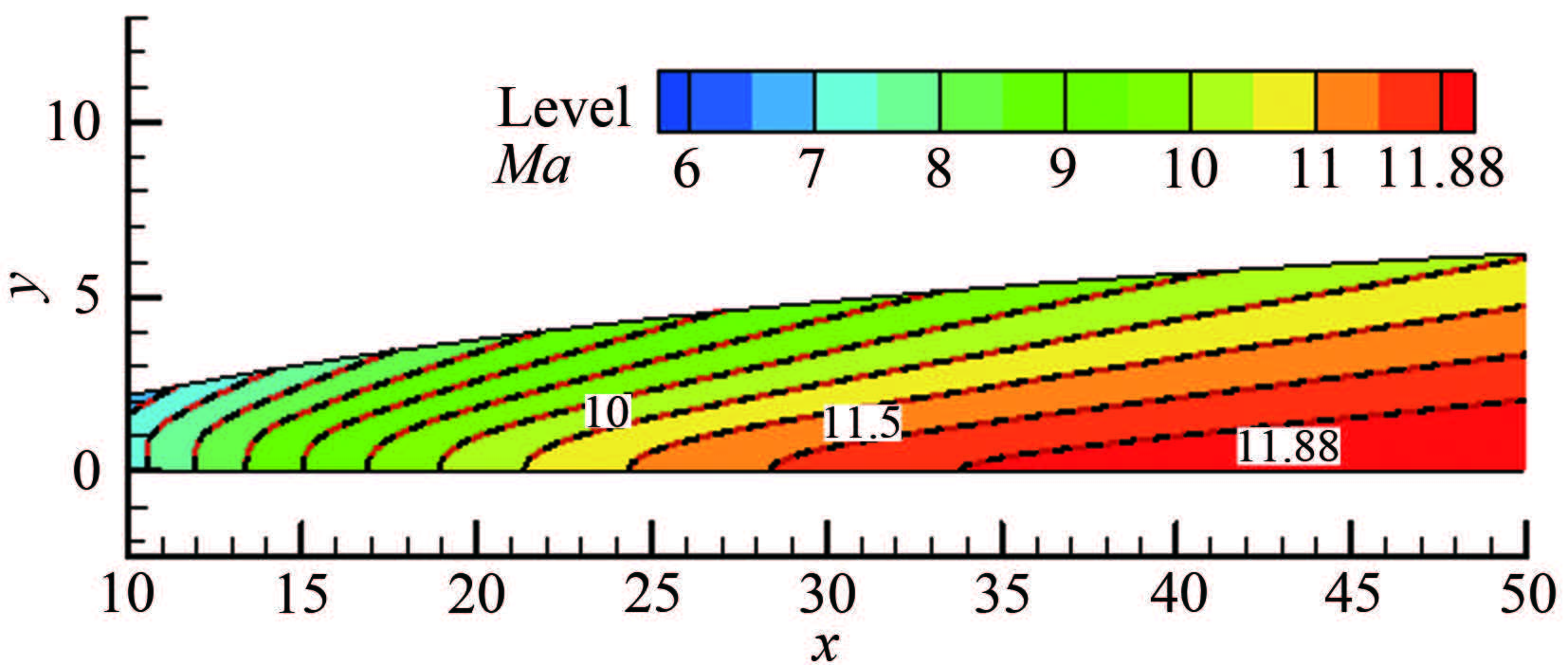
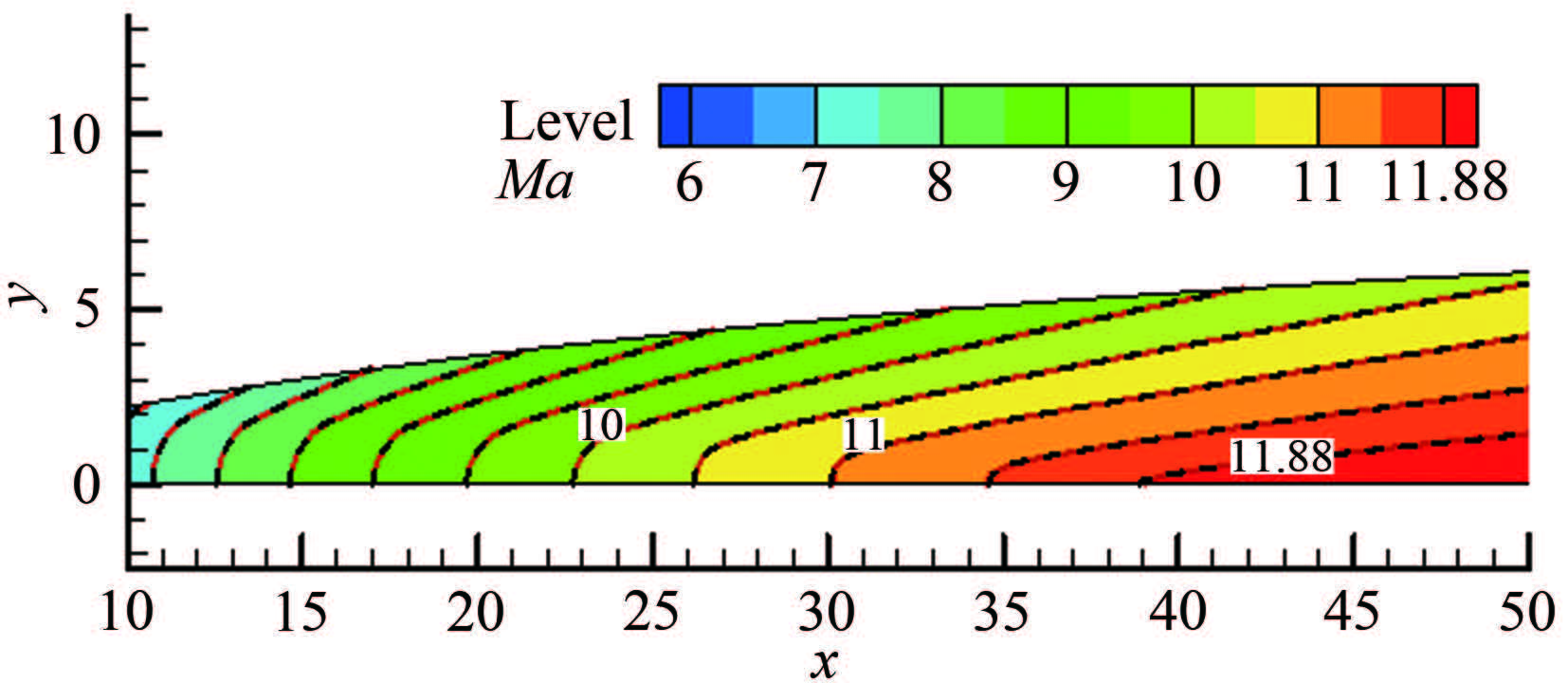
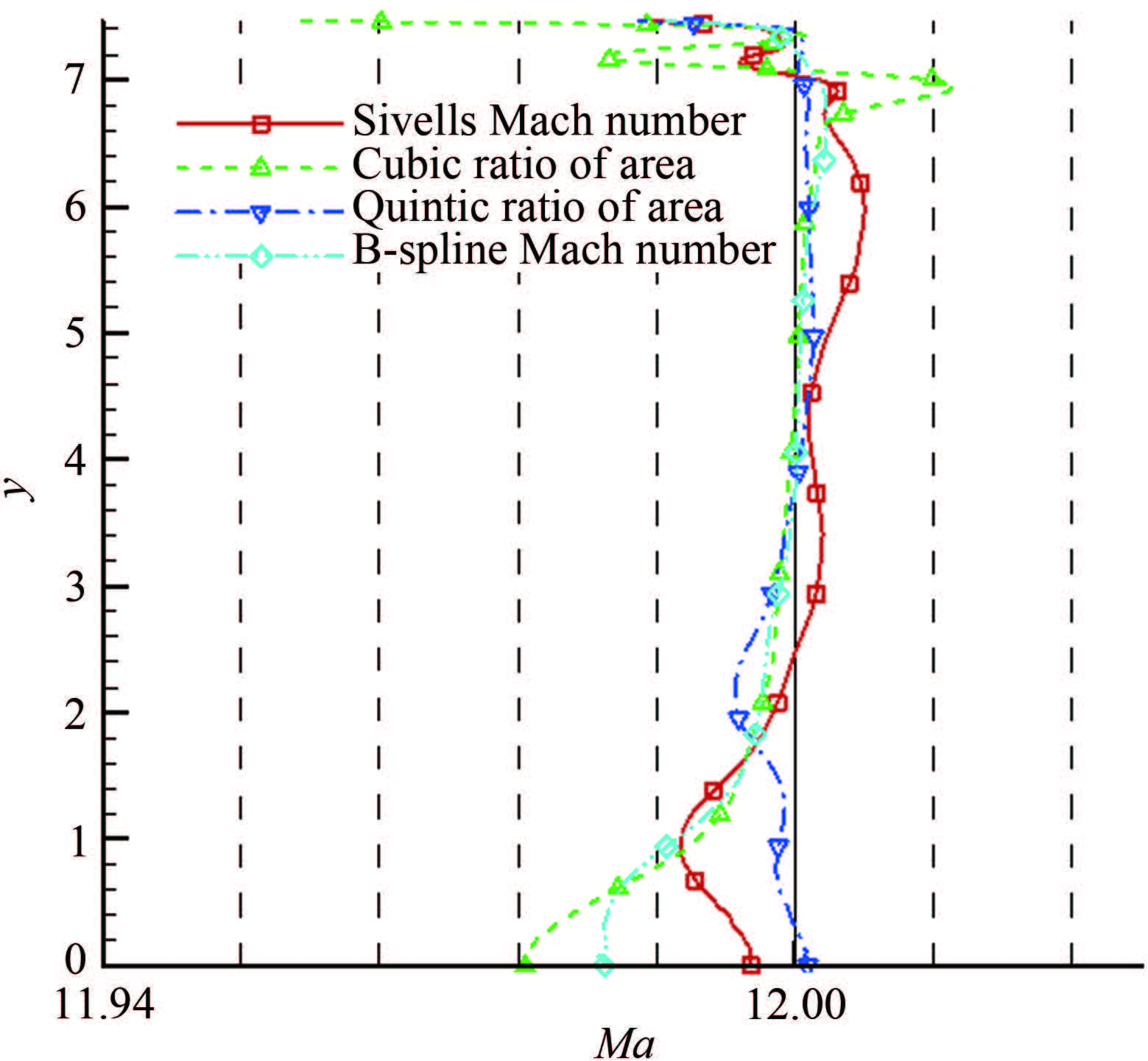
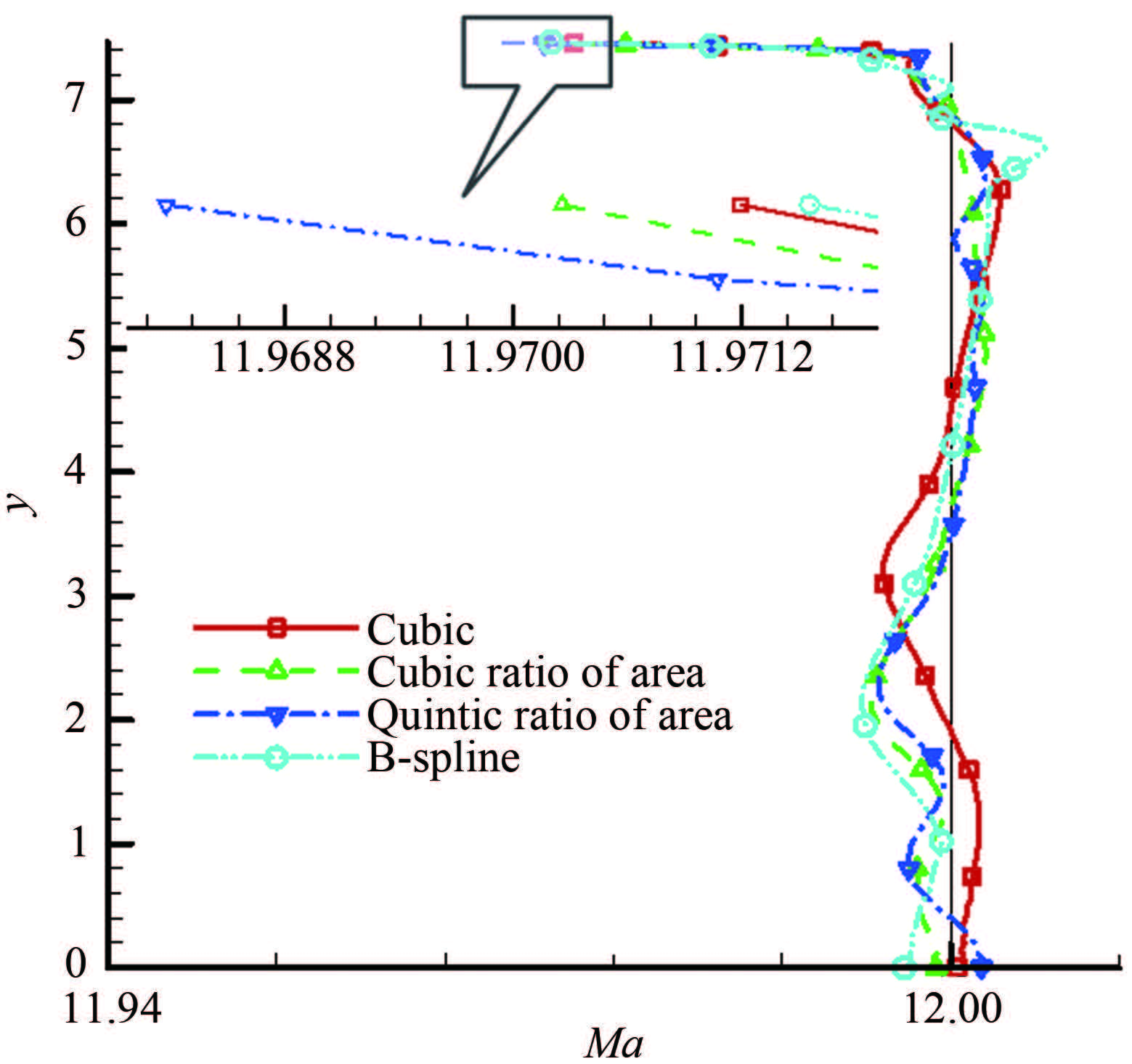
图 9~12给出了Case1~4的喷管设计流场马赫数等值线(特征线网三角化后的结果,红虚线)与数值模拟结果(黑实线)的比较,4种不同轴线马赫数分布的设计流场与数值模拟结果基本一致。实际上特征线方法计算的出口参数就是均匀的设计出口马赫数,只要数值过程足够精确,理论上特征线方法得到的型面应该就是能够产生均匀出口马赫数的型面。但是实际计算中,布点数、网格和数值过程等都带来误差,所以实际得到的喷管出口必然有一定的偏差,而这个偏差需要用数值模拟方法获得。图 9~12的结果表明特征线方法实际计算中的偏差并不明显,至少在云图上无法明确得出,但通过分析数值模拟的出口马赫数可以比较在相同设计参数和计算条件下,不同分布所带来的差异。图 13给出了Case1~4喷管的出口马赫数比较,其中面积比五次多项式分布和Sivells分布的最大偏差接近0.1%,B样条曲线分布的结果靠近轴线局部区域略大于0.1%,而面积比三次多项式分布的结果最大偏差为0.35%。图 14给出了Case5~8喷管的结果,其中因为面积比的三次多项式分布导致起点J附近的马赫数增长过快,所以取idx=0.8。除靠近壁面的区域外4种分布出口马赫数偏差均小于0.1%,壁面附近偏差最大的是面积比的五次分布,约为0.3%,最小的是B样条分布,但4种分布之间的差异小于0.03%。上述结果说明,在喷管长度、特征点分布和数量等设计参数一致时,采用不同的轴线马赫数分布函数对喷管出口马赫数存在影响,但只要采用合适的分布使得轴线马赫数正确合理,可以在除壁面附近外的区域得到出口马赫数偏差小于0.1%的结果。
|
| 图 9基于Sivells轴线马赫数分布预设的喷管马赫数等值线 Fig.9Mach number contour of the nozzle designed with the Sivells’ axial Mach number distribution |
|
| 图 10基于面积比三次多项式分布预设的喷管马赫数等值线 Fig.10Mach number contour of the nozzle designed with the cubic distribution of the ratio of area |
|
| 图 11基于面积比五次多项式分布预设的喷管马赫数等值线 Fig.11Mach number contour of the nozzle designed with the quintic distribution of the ratio of area |
|
| 图 12基于B样条曲线马赫数预设的喷管马赫数等值线 Fig.12Mach number contour of the nozzle designed with the B-spline Mach number distribution |
|
| 图 13不同轴线马赫数预设方法的喷管出口马赫数 Fig.13Mach number at exit of the nozzle designed with different axial Mach number presetting methods |
|
| 图 14不同轴线马赫数预设方法的喷管出口马赫数cF=3.0 Fig.14Mach number at exit of the nozzle designed with different axial Mach number presetting methods with cF=3.0 |
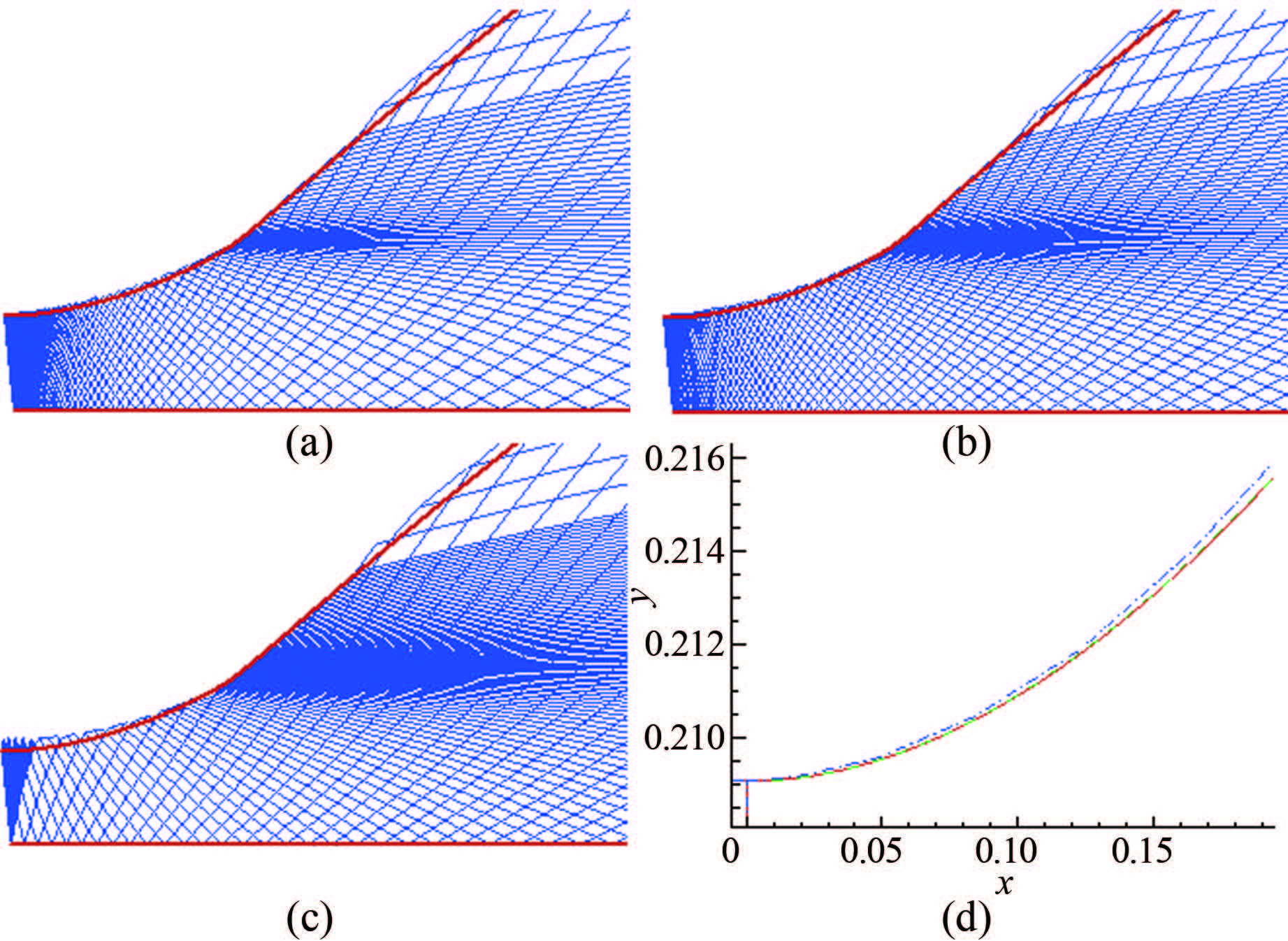
轴线上特征点的位置分布会明显影响特征线网,比如影响网格的过渡光滑性和正交性。图 15给出了马赫12喷管,轴线上马赫数三次多项式分布,轴线上点数101,出口马赫数线上点数101,轴线上的点采用双曲加密,两端加密参数分别为(a)0.999,0.5;(b)0.99,0.5;(c)0.9,0.5的特征线网,其中图 5(a)和 图5(b)在特征线网起始区域(J点附近)过渡明显好于图 5(c)。图 5(d)图中喷管无粘型面的差异反映了图 5(a)、5(b)和图 5(c)不同特征线网所导致的差异,表明特征线网是否过渡光滑是其质量的重要影响因素。
|
| 图 15轴线上不同布点的特征线网和喷管型面比较 Fig.15Comparision of characteristic networks and contours of different point distributions |
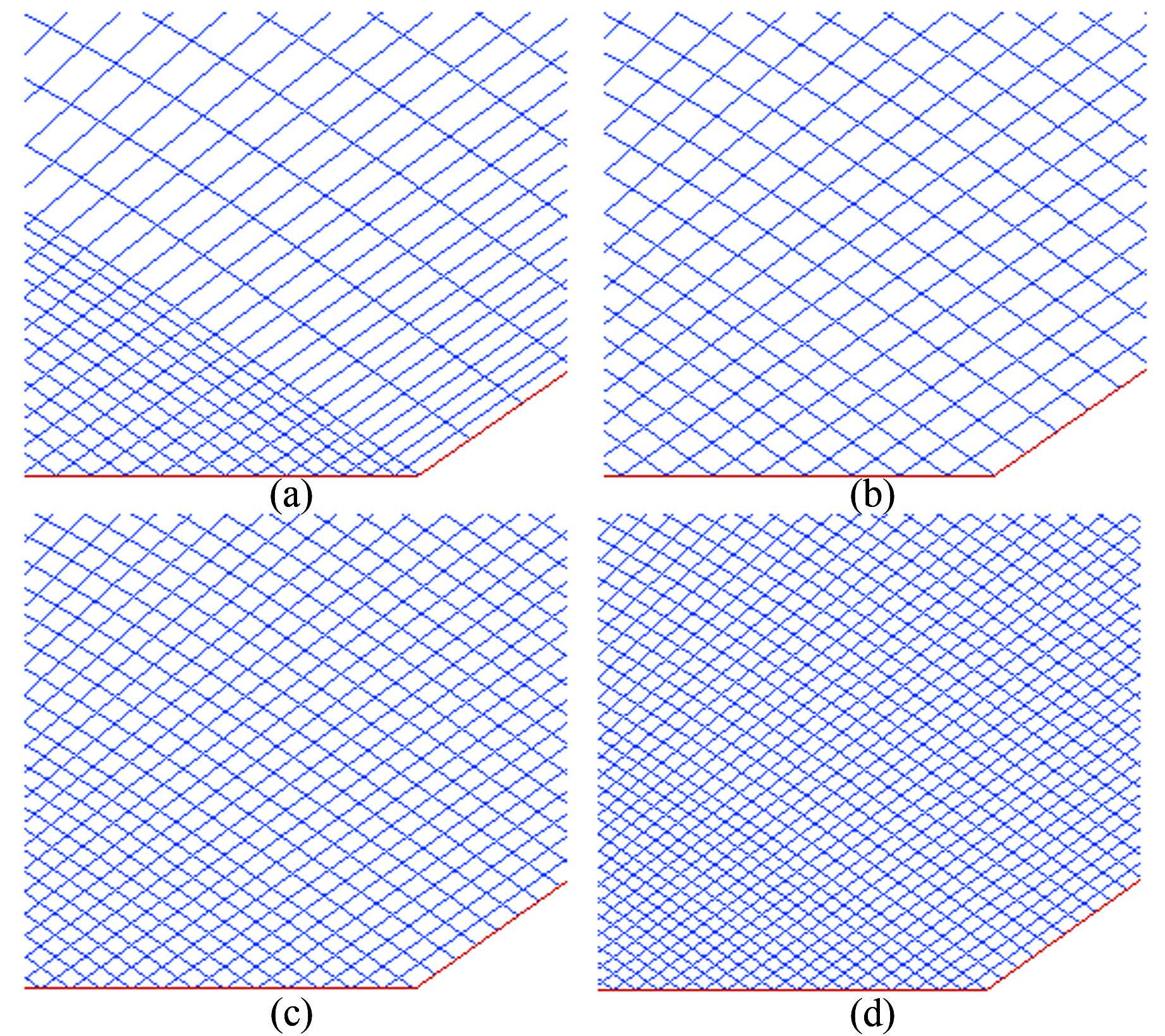
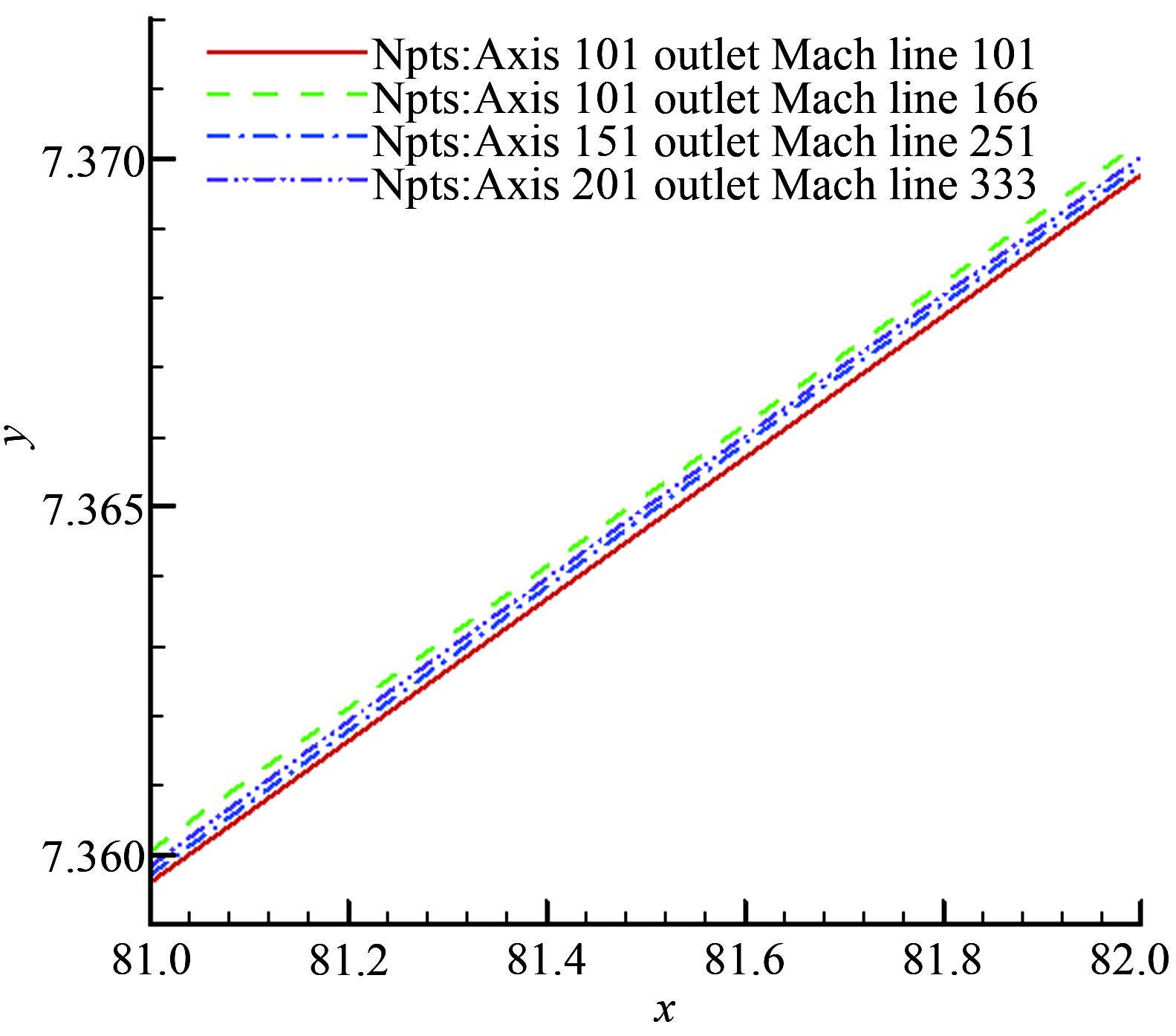
特征点的数量既影响特征线网疏密也影响其是否光滑过渡。图 16给出了采用4种不同布点数时在F点附近的特征线网,轴线上两端加密参数为0.999和0.5,其中轴线和出口马赫线分别为(a) 101,101; (b) 101,166; (c) 151,251; (d) 201,333。在图 16(a)中F点附近轴线和出口马赫线上的右行特征线过渡不够光滑,而图 16(b)、16(c)和16(d)相对较好。随着点数的增加特征线网也随之变密。图 17给出了喷管某位置的型面比较,可以看到采用不同点数时的细微差异。
|
| 图 16不同点数的特征线网(F点附近) Fig.16Comparision of characteristic networks of different point numbers (near F point) |
|
| 图 17不同点数的型面比较 Fig.17Comparision of contour of different point numbers |
采用数值模拟方法考察轴线和出口马赫线上点的数量和分布对于喷管流场的影响,考虑马赫12喷管,三次多项式轴线马赫数分布cF=3.0,初始线特征点数81,喉道曲率半径比12,转折角12°,泉流半径为1.0。计算如下状态:(Case1)轴线101双曲函数分布b1=0.999,b2=0.5,出口马赫线166,平均分布;(Case2)轴线151双曲函数分布b1=0.999,b2=0.5,出口马赫线251,平均分布;(Case3)轴线201双曲函数分布b1=0.999,b2=0.5,出口马赫线333,平均分布;(Case4)轴线151双曲函数分布b1=0.99,b2=0.5,出口马赫线251,平均分布;(Case5)轴线151多点控制分布(见1.2节),出口马赫线251,平均分布。
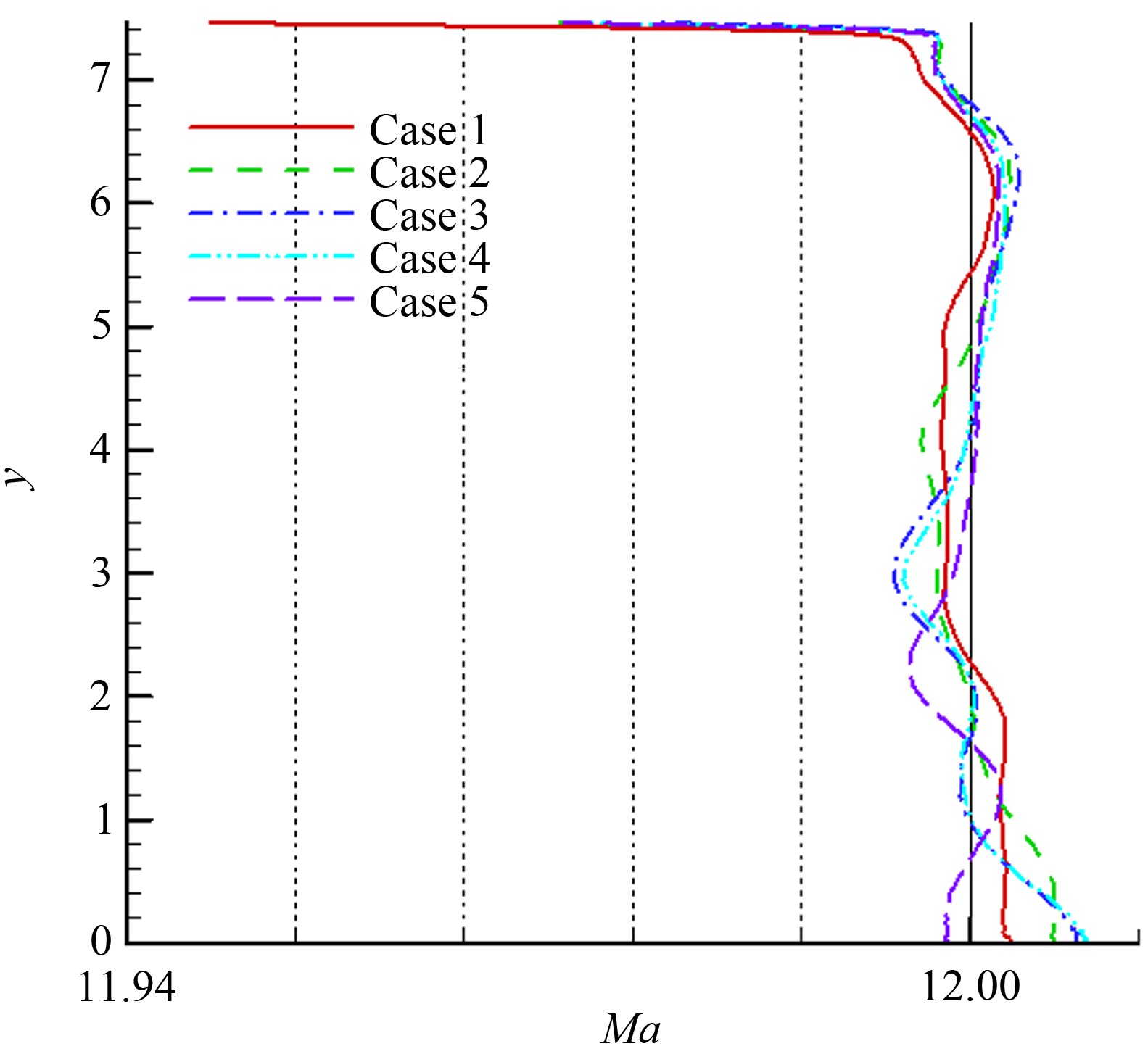
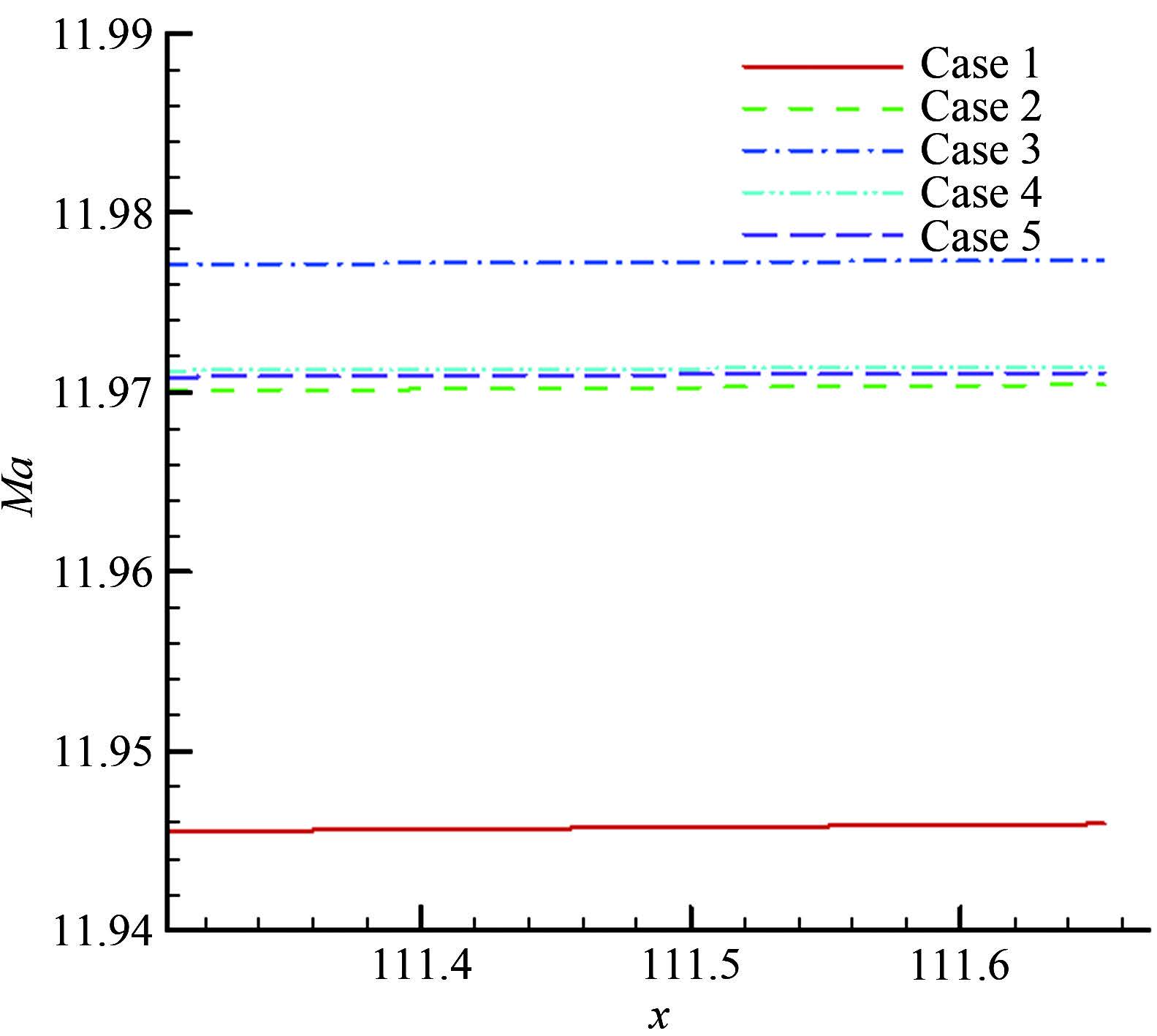
图 18的喷管出口马赫数表明,5个状态的结果在除靠近上壁面的区域外,偏差均在0.1%以内,不同状态在不同的y位置偏差各异。从图 19喷管上壁面的马赫数看,状态3最接近出口马赫数12,偏差约0.19%,而状态1的结果偏离最大达0.45%,说明当网格点数偏少时,计算结果偏离明显增大,随着网格点数增加,特征线网的精度明显增加。而状态2、4和5在相同点数情况下,轴线上特征点的不同分布会产生一定的差异,其中状态4的结果最接近出口马赫数,但3种结果偏差小于0.02%,结合图 15分析,首端加密参数b1大于0.99,使得特征线网过渡光滑,是特征线网质量的重要保证。
|
| 图 18喷管出口马赫数 Fig.18Mach number at exit of the nozzle |
|
| 图 19喷管上壁面马赫数 Fig.19Mach number at wall of the nozzle |
对于高超声速风洞喷管的无粘型面设计,基于预设轴线马赫数分布的直接设计方法是目前最普遍采用的方法。通过本文的研究得出如下结论:
(1) 对基于面积比的轴线马赫数分布设定的方法进行改进,使得在原方法保证轴线马赫数不超过出口马赫数的同时,提高了轴线上起点附近马赫数增长的合理性。采用多点控制的轴线特征点位置分布方法,提供了轴线特征点分布更大的自由度和可控度。
(2) 轴线上马赫数分布函数、特征点的分布和边界上特征点的数量影响特征线网的质量,进而影响喷管无粘型面。当采用某种分布函数保证轴线上马赫数分布合理,则可以保证出口马赫数除壁面附近外的绝大部分区域偏差小于0.1%。特征点数增加或者采用一定的特征点分布,使得特征线网过渡更光滑,能进一步减小壁面附近的出口马赫数偏差。
| [1] | Shope F L. Contour design techniques for super/hypersonic wind tunnel nozzles[C]. 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, 2006. |
| [2] | Korte J J, Kumar A, Singh D J, et al. CAN-DO, CFD-based aerodynamic nozzle design optimization program for supersonic/hypersonic wind tunnels[C]. AIAA 17th Aerospace Groud Testing Conference, Nashville, TN, 1992. |
| [3] | Shope F L. Design optimization of hypersonic test facility nozzle contours using splined corrections[R]. AEDC-TR-04-2, 2005. |
| [4] | Zucrow M J, Hoffman J D. Gas dynamics volume I~II[M]. New York: John Wiley & Sons Inc , 1976 . |
| [5] | Foelsch K. The analytical design of an axially symmetriclaval nozzle for a parallel and uniform jet[J]. Journal of the Aeronautical Sciences , 1949, 16 : 161–166. DOI:10.2514/8.11758 |
| [6] | Cresci R J. Tabulation of coordinates for hypersonic axisymmetric nozzle Part I-Analysis and coordinates for test section Mach number of 8, 12 and 20[R]. TN58-300, 1958. |
| [7] | Sivells J C. Aerodynamic design of axisymmetric hypersonic wind-tunnel nozzles[J]. Journal of Spacecraft , 1970, 7 (11) : 1292–1299. DOI:10.2514/3.30160 |
| [8] | Sivells J C. A computer program for the aerodynamic design of axisymmetric and planar nozzles for supersonic and hypersonic wind tunnels[R]. AEDC-TR-78-63, 1978. |
| [9] | 易仕和, 赵玉新, 何霖, 等. 超声速和高超声速喷管设计[M]. 北京: 国防工业出版社 ,2013 . Yi S H, Zhao Y X, He L, et al. Supersonic and hypersonic nozzle design[M]. Beijing: National Defense Industry Press , 2013 . |
| [10] | Tajfar A H, Hall I M. Design of a nozzle for a hypersonic wind tunnel. AERO-REPT-9113, ETN-92-92779[M]. , 1991 . |
| [11] | 张敏莉, 易仕和, 赵玉新. 超声速短化喷管的设计和试验研究[J]. 空气动力学学报 , 2007, 25 (4) : 500–503. Zhang M L, Yi S H, Zhao Y X. The design and experimental investigations of supersonic length shorted nozzle[J]. Acta Aerodynamica Sinica , 2007, 25 (4) : 500–503. |
| [12] | 赵一龙, 赵玉新, 王振国, 等. 超声速型面可控喷管设计方法[J]. 国防科技大学学报 , 2012, 34 (5) : 1–4. Zhao Y L, Zhao Y X, Wang Z G, et al. Designing method of supersonic nozzle with controllable contour[J]. Journal of National University of Defense Technology , 2012, 34 (5) : 1–4. |
| [13] | Shapiro A H. The dynamics and thermodynamics of compressible fluid flow[M]. New York: The Ronald Press Company , 1953 . |
| [14] | Moger W C, Ramsay D B. Supersonic axisymmetric nozzle design by mass flow techniques utilizing a digital computer[R]. AEDC-TDR-64-110, U. S. Air Force, 1964. |
| [15] | 王永. 非结构化网格生成技术及在SIMPLE算法中的应用研究[D]. 天津: 天津大学, 2005. Wang Y. The study on generation techniques of unstructured grid and application in SIMPIE algorithm[D]. Tianjin: Tianjin University, 2005. |
| [16] | Hall I M. Transonic flow in two-dimensional and axially-symmetric nozzles[J]. Quarterly Journal of Mechanics and Applied Mathematics. XV , 1962, 15 (4) : 487–508. DOI:10.1093/qjmam/15.4.487 |
| [17] | Kligel J R, Levine J N. Transonic flow in small throat radius of curvature nozzles[J]. AIAA , 1969, 7 (7) : 1375–1378. DOI:10.2514/3.5355 |
| [18] | 施法中. 计算机辅助几何设计与非均匀有理B样条(CAGD&NURBS)[M]. 北京: 北京航空航天大学出版社 ,1994 . |
| [19] | Piegl L, Tiller W. The NURBS book[M]. New York: Springer , 1997 . |



