粒子图像测速技术(Particle Image Velocimetry,PIV)是一种发展迅速并得到广泛应用的流场测量手段。PIV属于无接触式测量技术,能够即时测量整个流场的瞬时速度,并且具有很高的测量精度。随着PIV硬件的发展(包括高速CMOS相机和高能激光器)、图像处理技术的进步以及高性能计算机设备的支持,粒子图像测速技术已经日趋完善[1]。
流场的压力分布是流体运动的重要动力学特征,它决定了流场中物体的受力情况,同时也是气动噪声及结构振动的主要来源[2]。例如,对于湍流流动、空腔流动和气动声学现象而言,脉动压力的测量都是至关重要的[3]。同样地,在确定物体壁面的受力情况时,不论是定常流动还是非定常流动,压力场的精确测量也十分关键。与壁面压力的测量相比,流场内部瞬时静压分布的测量难度更大。传统的测压技术受制于接触式测量、非瞬时测量和有限点测量3个主要缺陷,已经不能满足流场动力学现象的研究[4]。
目前,国内外许多学者都在探索流体静压场的测量方法,其中基于PIV瞬时速度场重构压力场的方法具有巨大优势[5]。Gurka等[6]最早提出了不可压缩流体基于PIV速度场重构压力场的基本原理,并通过收缩管流和冲击射流2个算例进行了验证。Hosokawa等[7]运用SOLA迭代方案计算了层流管流、层流粒子绕流和层流气泡绕流等3个流场的瞬时压力场,并与数值模拟结果进行了对比,获得了较高的精度。Fujisawa等[8]针对微小通道的三通节点部位运用PIV速度场重构了压力场,并对其流动规律进行了较为细致的分析。Tanahashi等[9]重点运用PIV重构压力场的方案研究了圆柱绕流的受力情况,并考虑了周期性震荡因素,体现了基于PIV速度场重构压力场的方法对于流场受力分析的应用。Oudheusden等[10-11]初步探索了可压流场基于PIV重构压力场的基本原理,并以翼型绕流为例进行了初步验证,随后,他们又对带有激波的可压流场进行了测量,并获得了精度较好的压力场。
尽管很多研究证实了基于PIV速度场重构压力场原理的正确性与可行性,但是很少有学者对压力场 重构算法进行系统性的误差分析。Charonko等[12]曾对基于PIV瞬时速度场重构瞬时压力场的算法进行了较为细致的评估,考虑了不同的重构算法、不同的时空分辨率以及速度场的误差对重构压力场精度的影响。De Kat等[13-16]运用Time-resolved PIV获得的速度场数据,得到了方块绕流流场的压力分布,同时分析了影响重构压力场精度的主要因素,主要包括重构压力场的噪声响应与峰值相应随时空分辨率的变化、欧拉法与拉格朗日法的区别以及不同的重叠因子对重构压力场的影响。但是,以上研究均没有分析噪声、速度场误差以及分辨率对有限容积法的影响程度,也没有考虑不同的插值算法和不同类型的边界条件及其精度对重构压力场的影响。
本文针对不可压缩流体论述了3种基于PIV速度场重构压力场的基本原理及计算方法,包括有限容积法、直接积分法和Poisson方程法,然后通过管流突扩流场和偏置方块绕流流场验证了算法的正确性,同时分别研究了噪声、速度场精度、插值算法以及边界条件的类型与精度对重构压力场的影响,并对比了3种重构算法的差异。最后针对管流突扩过程第20ms的流场,给出了3种重构算法下的压力场云图以及对应的CFD模拟结果。需要说明的是,本文所开展的工作主要是理论研究,因此上述流场及结论均基于CFD数值模拟的速度场数据。
1 基本原理及计算方法对于不可压缩流体而言,基于PIV速度场重构压力场的基本原理是Navier-Stokes方程。通过对不可压Navier-Stokes方程进行不同的变形转换,可以得到不同的压力场重构算法。
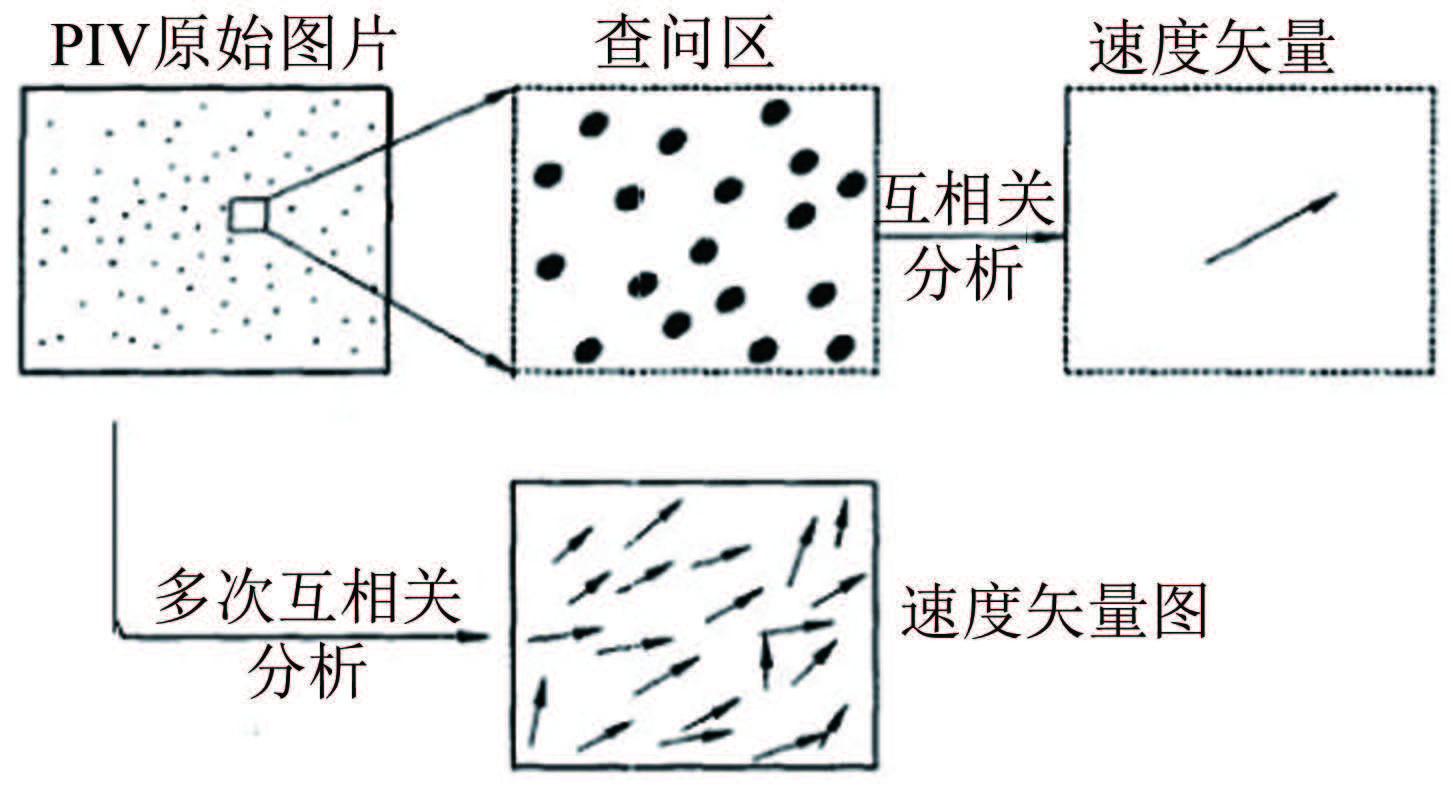
1.1 有限容积法在PIV图像处理过程中,一般将图像分为许多矩形小区域,称为PIV查问区[17-18],其面积取决于相机的空间分辨率。通过对相邻图像的查问区进行互相关处理分析,可以得到2个相邻时刻粒子的平均位移,根据2幅图像的时间间隔,就可以得到流场的速度矢量分布图,即最终的速度场[19-20],如图 1所示。PIV的图像处理方式与采用内节点法的矩形区域同位网格十分类似,两者均是将矩形区域内的各物理量赋值于几何中心点。事实上,PIV图像中各个查问区与同位网格中相应节点的控制容积一一对应[21]。
二维不可压缩流体的Navier-Stokes方程为:
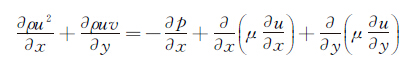 (1)
(1)
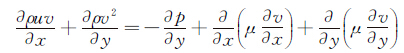 (2)
(2)
将以上方程改写为如下形式:
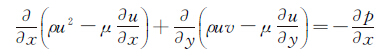 (3)
(3)
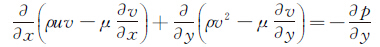 (4)
(4)
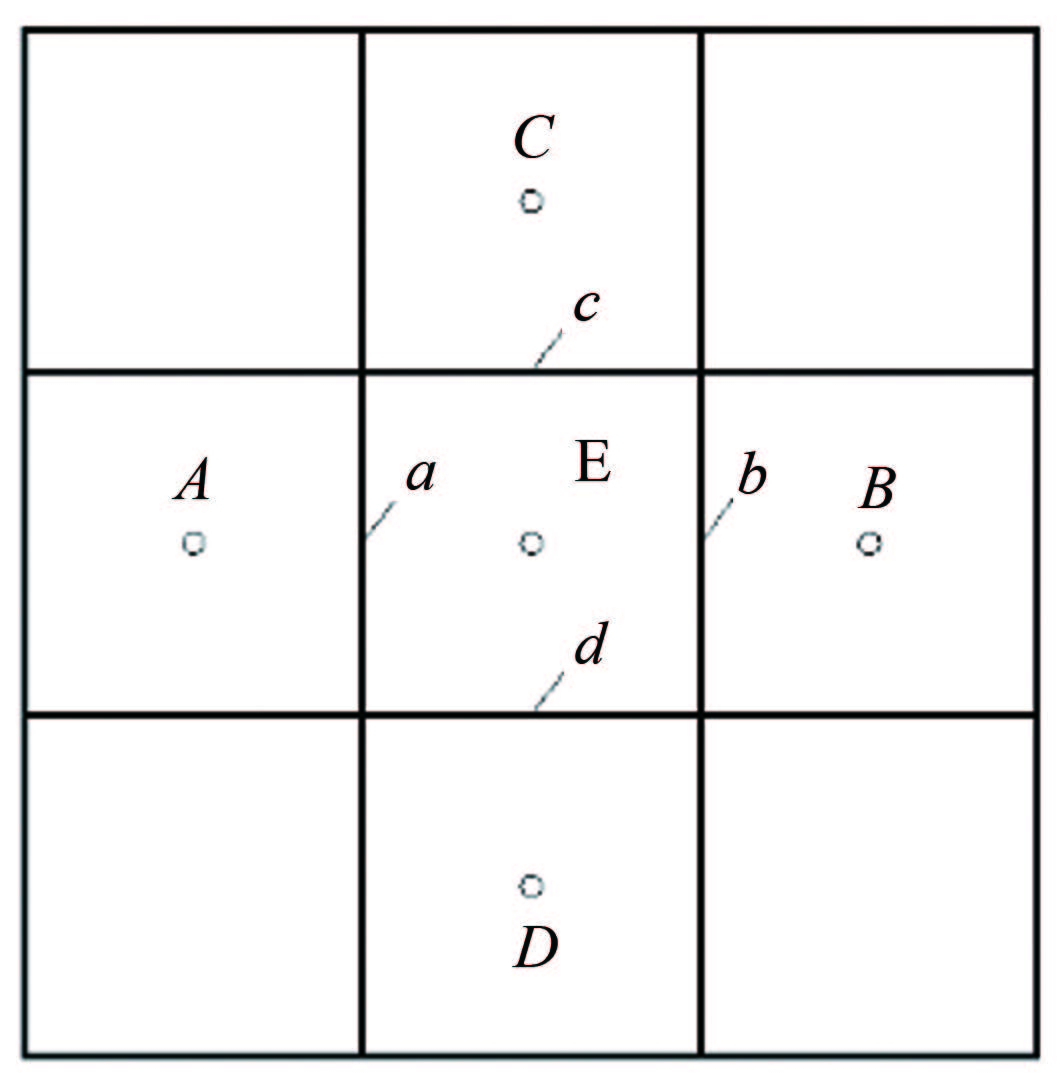
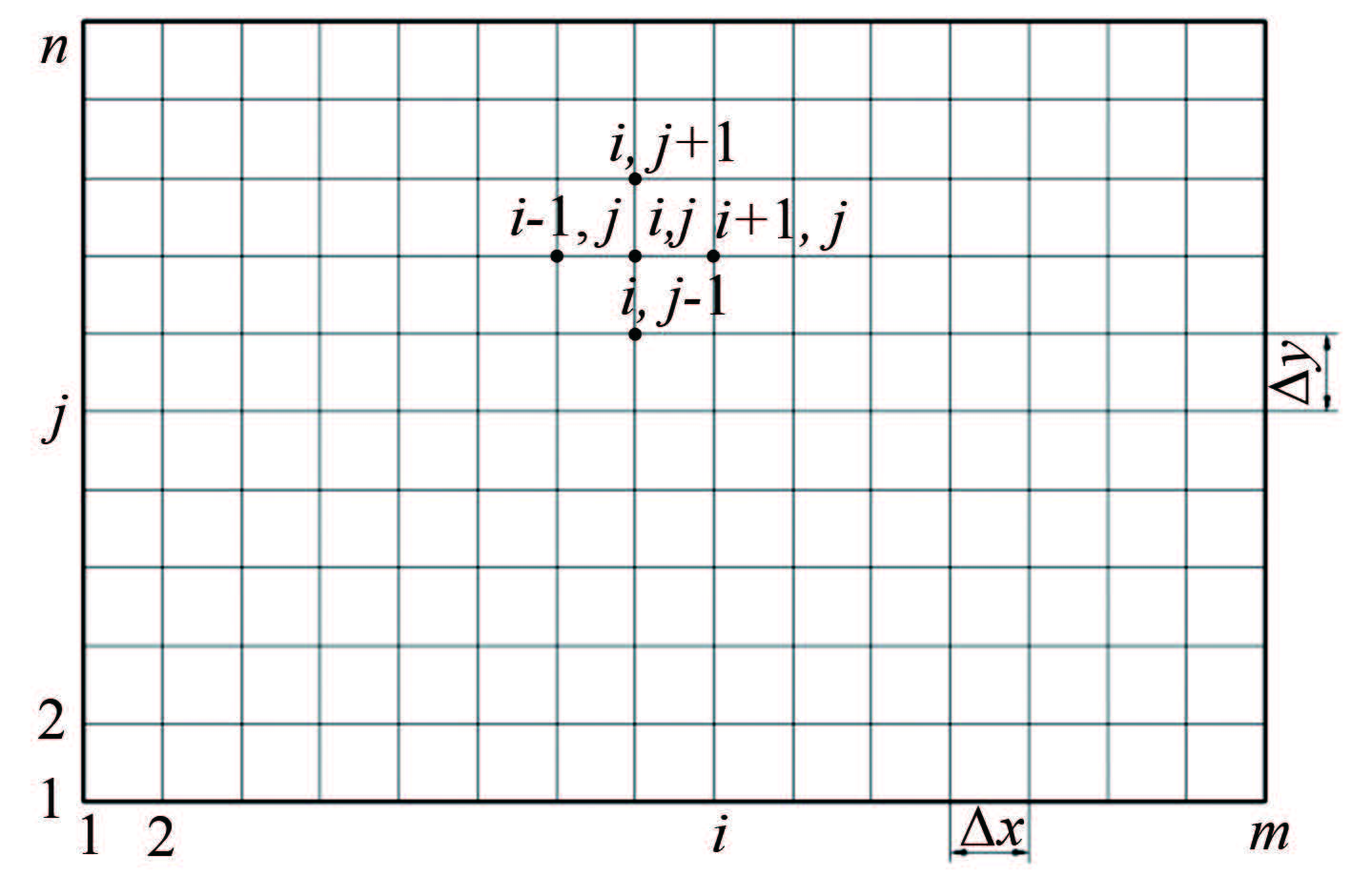
若ρ和μ已知,且u和v已由PIV测得,假定Δx=Δy=h,则按照图 2所示的二维同位网格,将上述方程的各项对矩形小区域进行积分,得:
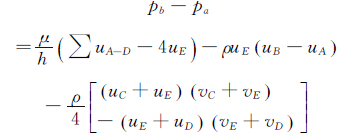 (5)
(5)
同样地,有:
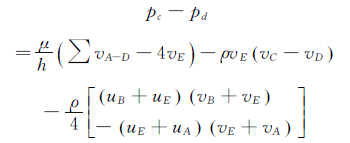 (6)
(6)
给定合适的边界条件,根据各个网格节点之间沿水平及垂直方向的压力差值,求得各个节点的压力值,从而得到完整的重构压力场。
1.2 直接积分法对于不可压缩流体而言,若流体的密度和粘性系数已知,且测得流场的瞬时速度场和瞬时加速度场,就可以通过Navier-Stokes方程计算出流场的压力梯度[22],即:
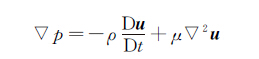 (7)
(7)
其中,Du/Dt是流场的加速度,若使用欧拉法,则流场中粒子的加速度可表示为:
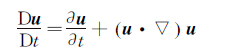 (8)
(8)
因此,当PIV测得流体的瞬时速度场以后,通过计算流场中粒子的加速度项Du/Dt以及粘性项μ▽2u,就可得到流场的压力梯度,即:
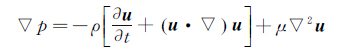 (9)
(9)
将上述矢量方程展开为方程组,得:
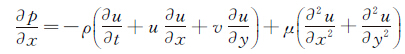 (10)
(10)
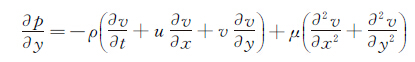 (11)
(11)
按照图 3所示对上述方程组进行有限差分,得:
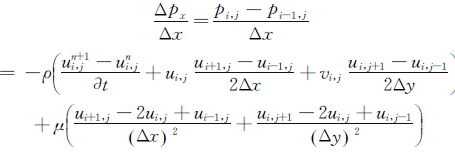 (12)
(12)
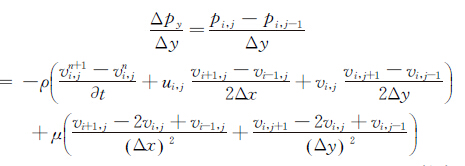 (13)
(13)
则流场中相邻节点之间的压力差为[24]:
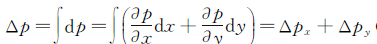 (14)
(14)
为了减小误差,考虑把沿不同路径积分得到的压力值进行平均,即:
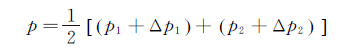 (15)
(15)
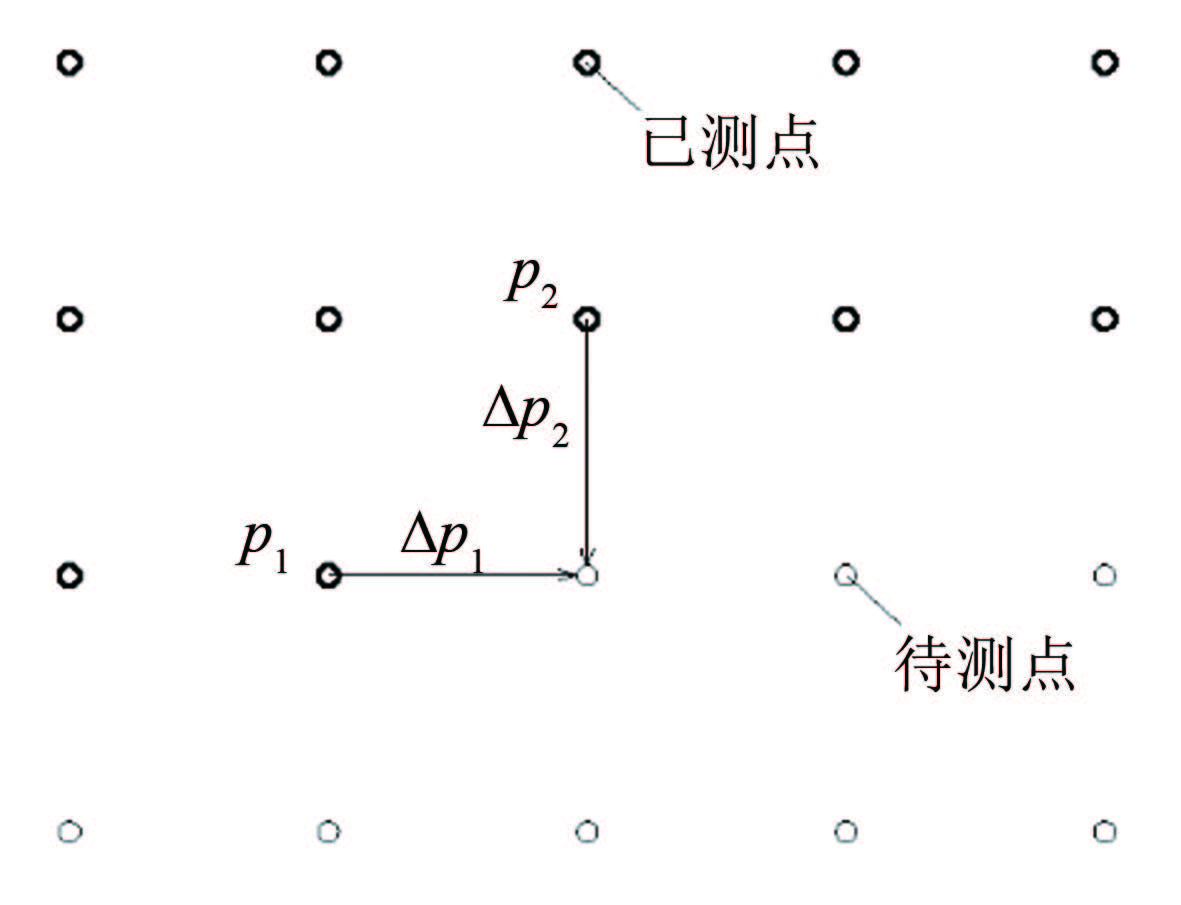
通过给定适当的边界条件,结合上述算法,按照图 4所示的方案进行积分,即可得到整个流场的压力分布。
1.3 1Poisson方程法 1.3.1 基本原理事实上,Poisson方程法是直接积分法的延续。通过对直接积分法中的流场压力梯度公式进行标准的五点差分,可以得到用于重构流场压力分布的Poisson方程如下[22]:
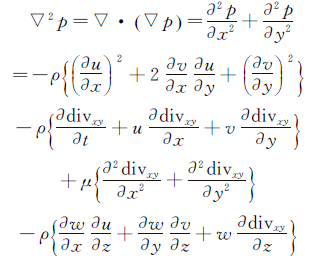 (16)
(16)
其中,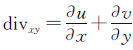
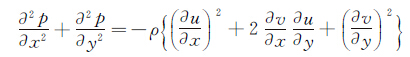 (17)
(17)
在上述Poisson方程中,所有的非定常项和粘性项都约去了。然而,Poisson方程的这种性质并不意味着最终的瞬时压力场与时间无关[22],这是因为在流场的边界条件中仍然包含时间项,例如压力梯度的计算方程。
总之,基于PIV速度场重构压力场的Poisson方程法大致分为3步:(1)使用PIV获取全场的速度分布;(2)计算流场的速度梯度并带入Poisson方程;(3)采用适当的边界条件求解Poisson方程从而得到整个流场的压力分布。
1.3.2 数值计算方法通过对Poisson方程进行有限差分,并结合适当的边界条件进行黎曼迭代,即可计算出整个流场的压力分布。Poisson方程解的存在唯一性和差分方程解的收敛性在数学上已被证明。理想情况下,测定流场中一点的压力值,然后结合诺依曼边界条件求解Poisson方程,即可获得全流场的压力分布。
首先将二维不可压缩流场的Poisson方程改写为以下形式:
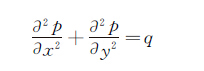 (18)
(18)
其中:
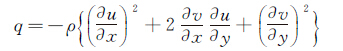 (19)
(19)
同样按照图 3所示对上述方程进行有限差分,得:
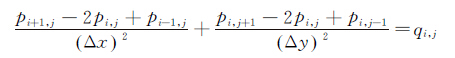 (20)
(20)
假设PIV查问区采用正方形,且边长为h,即Δx=Δy=h,则上式化简为:
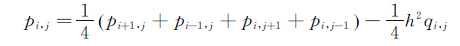 (21)
(21)
黎曼迭代的本质是利用非定常方程求定常解。Poisson方程是定常方程,为此建立一个非定常方程:
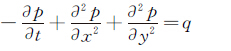 (22)
(22)
当时间t足够长时,p不再随时间变化,即达到定常状态,方程转化成定常方程,这时的解就是二维Poisson方程的解。
构造对上述方程的时间向前空间中心的有限差分公式,即:
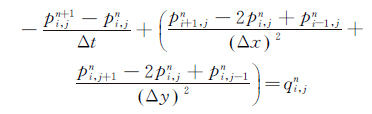 (23)
(23)
由于Δx=Δy=h,令Δt/h2=1/4,得:
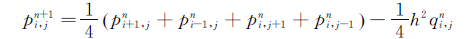 (24)
(24)
按照从上到下、从左到右的顺序进行求解,则在计算(i,j)节点第n+1时间层的函数值pn+1i,j时,(i-1,j)和(i,j-1)点第n+1时间层的函数值pn+1i-1,j和pn+1i,j-1已经求出,则将上式改写为:
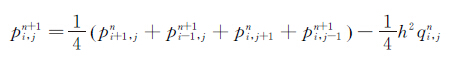 (25)
(25)
上式即为Poisson方程的黎曼迭代公式。
1.4 测量结果的评定标准评价基于PIV速度场重构的压力场精度一般采用误差的均方根值(Root Mean Square,RMS)。由于无法通过实验的方法直接测量流体的压力场,因此一般将基于PIV重构的压力场与数值模拟的结果作对比。采用测量区域内网格节点上重构压力值与数值模拟结果的绝对偏差相对于测量区域内最大压降的比值作为衡量重构压力场精度的标准,则重构压力场误差的均方根值为:
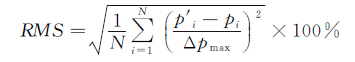 (26)
(26)
其中,N代表网格节点总数,p′i为重构压力值,pi为数值模拟的压力值,Δpmax代表测量区域相对于来流的最大压降。
虽然基于PIV速度场重构的压力场是通过数值计算得到的,但其依据的是PIV测得的速度场,且重构压力场的算法本质上是Navier-Stokes方程,该方程适用于绝大部分真实流体的流动现象,因此,基于PIV速度场重构压力场的方法从本质上讲属于一种间接的流场测量方法,它综合考虑了实际条件下的各种误差,包括模型的加工误差,仪器的系统误差、读数误差以及大气环境误差等。
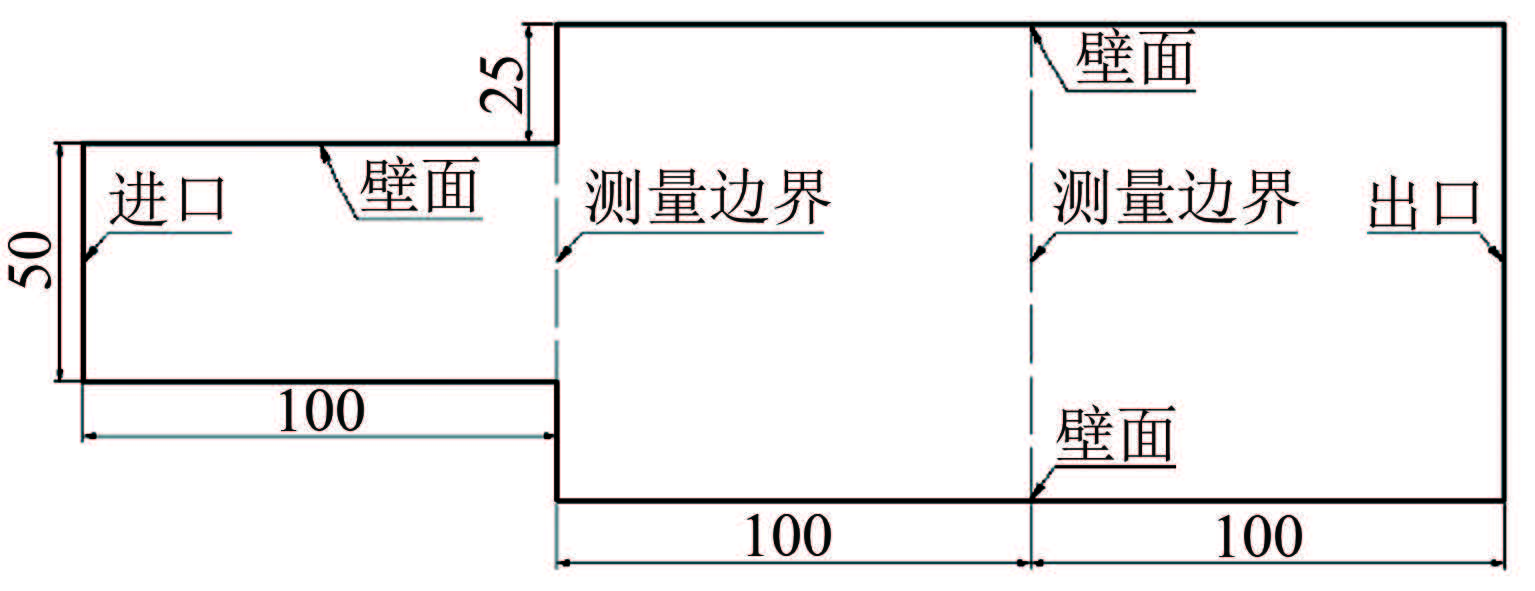
2 流场模型和模拟结果 2.1 管流突扩流场流场模型如图 5所示,其中,进口处空气的总压为标准大气压,整个流场的流速小于100m/s,可视为不可压缩流体,空气密度为1.225kg/m3,动力粘性系数为1.7894×10-5kg/(m·s),出口处的压力为101kPa。测量边界所围成的面积为PIV的测量区域,基于PIV速度场重构的压力场同样针对该区域。
|
| 图 5管流突扩流场模型 Fig.5The model of pipe flow with a sudden expansion |
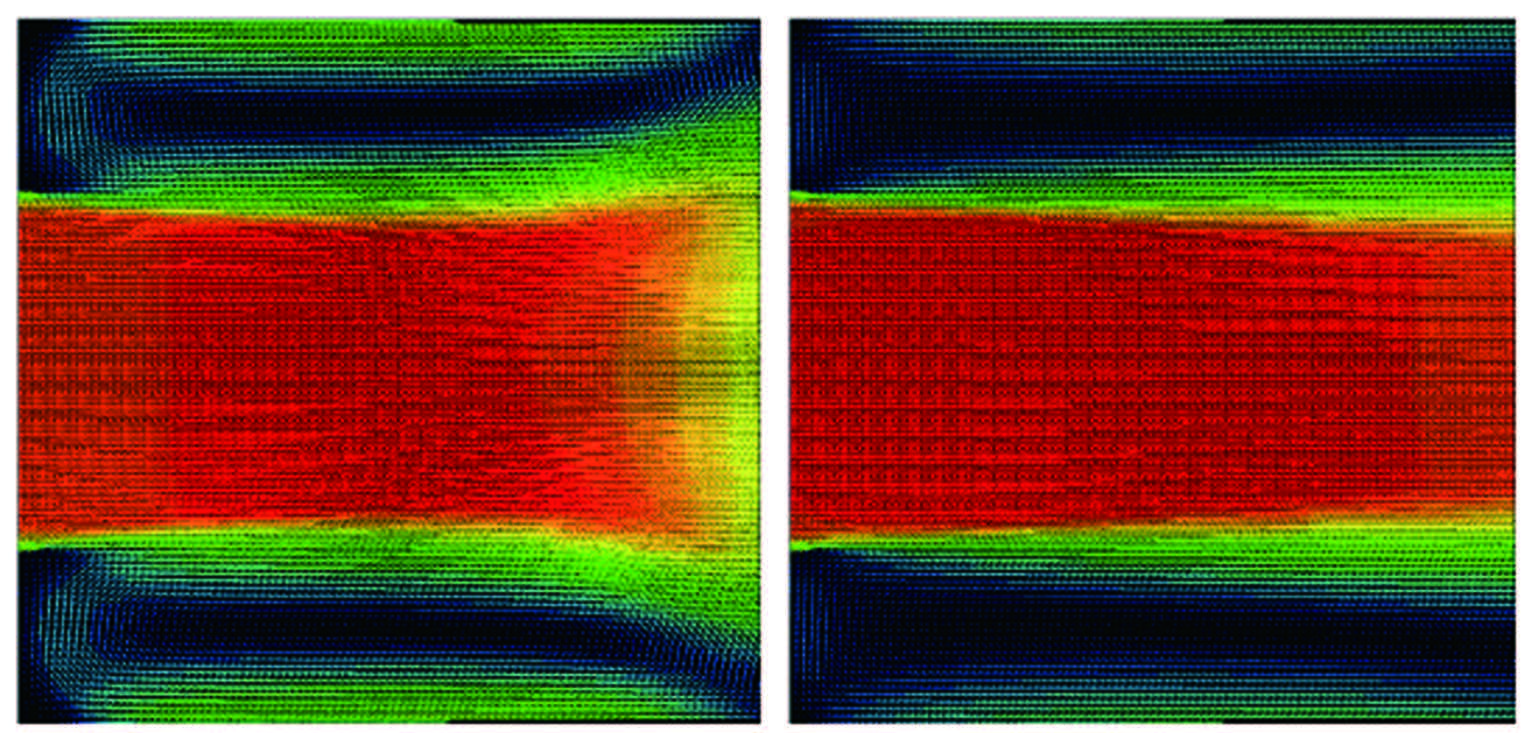
图 6是基于CFD获取的管流突扩过程中第20ms和第40ms的速度场图像,这里将其视为模拟PIV测得的速度场数据。其中,CFD计算采用的网格边长为0.1mm。
|
| 图 6管流突扩过程中的模拟PIV速度场 Fig.6Simulated PIV velocity fields during the process of pipe flow |
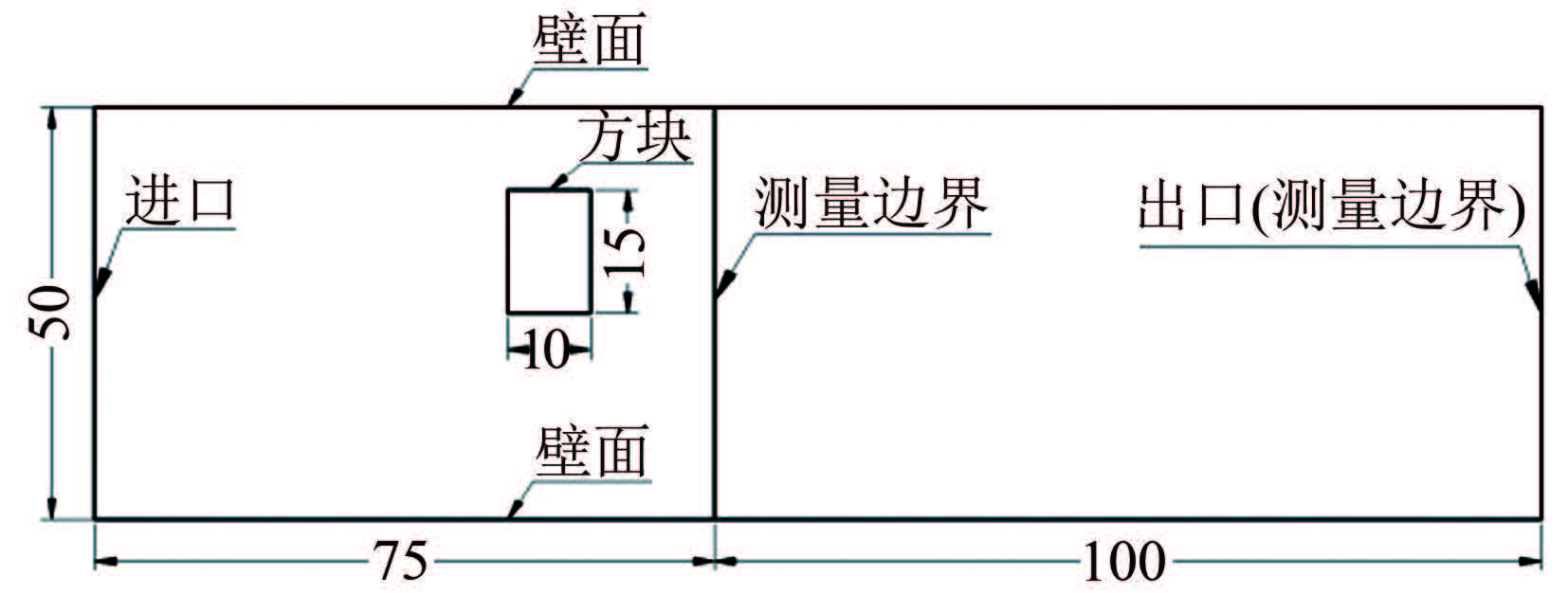
流场模型如图 7所示,其中,进口处空气的总压为标准大气压,整场流速小于100m/s,可视为不可压缩流体,空气密度为1.225kg/m3,动力粘性系数为1.7894×10-5kg/(m·s),出口处的压力为98000Pa。测量边界所围成的面积为PIV的测量区域,基于PIV速度场重构的压力场同样针对该区域。
|
| 图 7偏置方块绕流流场模型 Fig.7The model of the flow around a square |
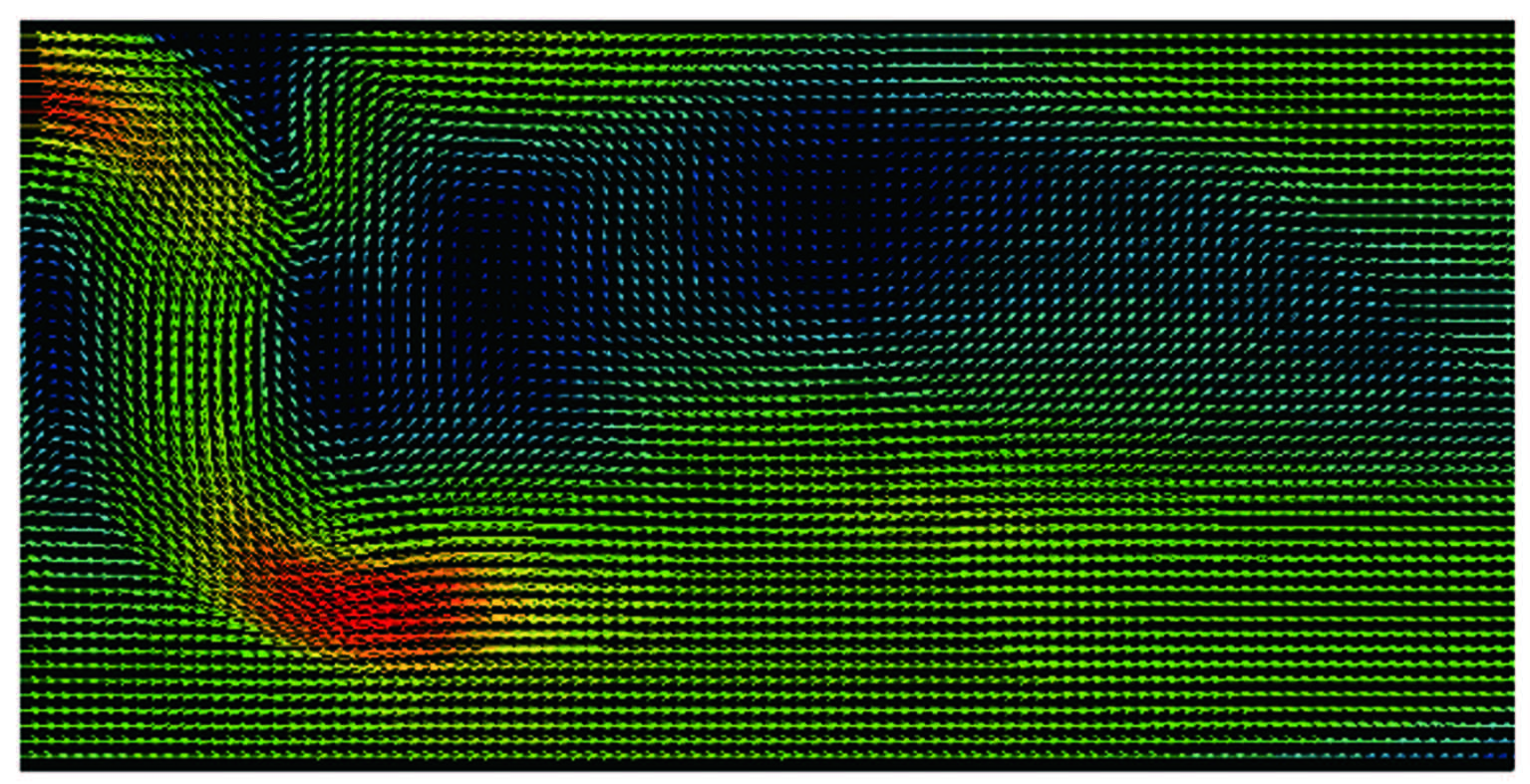
图 8为偏置方块绕流流场在第0.5s时刻的模拟PIV速度场图像。其中,CFD计算采用的网格边长为0.1mm。
|
| 图 8偏置方块绕流模拟PIV速度场图像 Fig.8Simulated PIV velocity field of the flow around a square |
本节主要运用有限容积法、直接积分法和Poisson方程法3种压力场重构算法,基于上述模拟PIV速度场图像,对管流突扩流场和偏置方块绕流流场进行了压力场重构;针对PIV实际测量过程中产生的噪声和速度场误差对不同重构算法下压力场精度的影响以及3种重构算法之间的差异进行了较为细致的分析;对比了压力场重构过程中不同插值方法的特点和优劣,并进行了相应的误差分析;研究了不同类型的边界条件及其精度对重构压力场误差的影响。
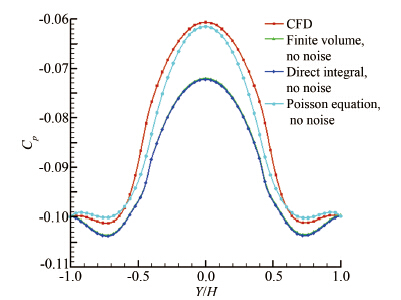
3.1 噪声对重构压力场的影响根据管流突扩过程中第40ms得到的模拟PIV速度场,分别运用上述3种压力场重构算法,得到相应的重构压力场,其中,PIV查问区边长取0.5mm。为了更加直观地分析3种不同算法下重构压力场的压力分布,以距离左侧测量边界40mm处的截面(高度为H)为研究对象,得到相应的重构压力分布曲线如图 9所示。
|
| 图 9距左侧测量边界40mm处截面的压力分布(无噪声) Fig.9Pressure distribution of the cross section at 40mm from the left side of the measurement area (no noise) |
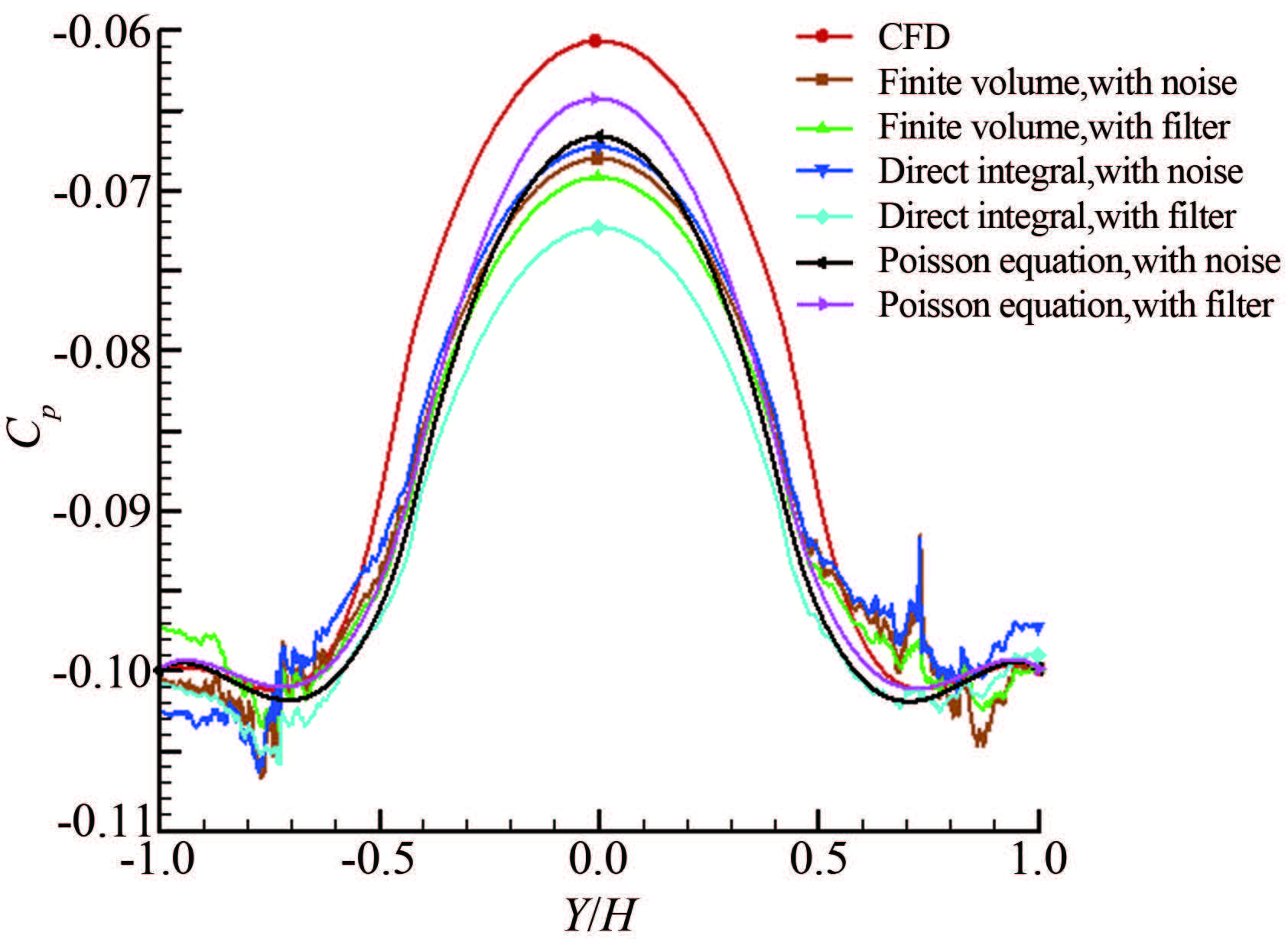
由于CFD计算得到的模拟PIV速度场是理想条件下的数据,其中不包含任何噪声与误差。因此,针对管流突扩流场第40ms的模拟PIV速度场,加入高斯白噪声,强度为流场平均速度的1%,采用不同的重构算法得到相应的压力分布。然后,使用中值滤波器进行降噪处理,得到滤波之后的压力分布曲线,并与未滤波的压力分布进行对比,结果如图 10所示。
|
| 图 10距左侧测量边界40mm处截面的压力分布(有噪声或滤波) Fig.10Pressure distribution of the cross section at 40mm from the left side of the measurement area (with noise or filter) |
可以发现,与CFD计算得到的压力分布相比,基于理想PIV速度场重构得到的压力场具有良好的精度,3种重构算法的正确性得到验证。理想PIV速度场加入高斯白噪声之后,若采用有限容积法和直接积分法进行压力场重构,则壁面附近的重构压力产生了剧烈的震荡,影响了重构压力场的光滑程度。若使用中值滤波器对PIV速度场进行滤波处理,则可以显著降低重构压力的震荡。对于Poisson方程法而言,数值试验和理论分析都表明其求解过程相当于对PIV速度场进行了预先的滤波处理,在物理上表现为低通滤波器的特性[15]。所以,Poisson方程法得到的重构压力分布不易受噪声的影响而产生震荡,同时,使用中值滤波器对PIV速度场进行滤波后,可以在一定程度上提高Poisson方程法的精度。因此,在实际实验过程中,有必要采用滤波器对PIV速度场进行预先的降噪处理从而提高重构压力场的光滑程度。
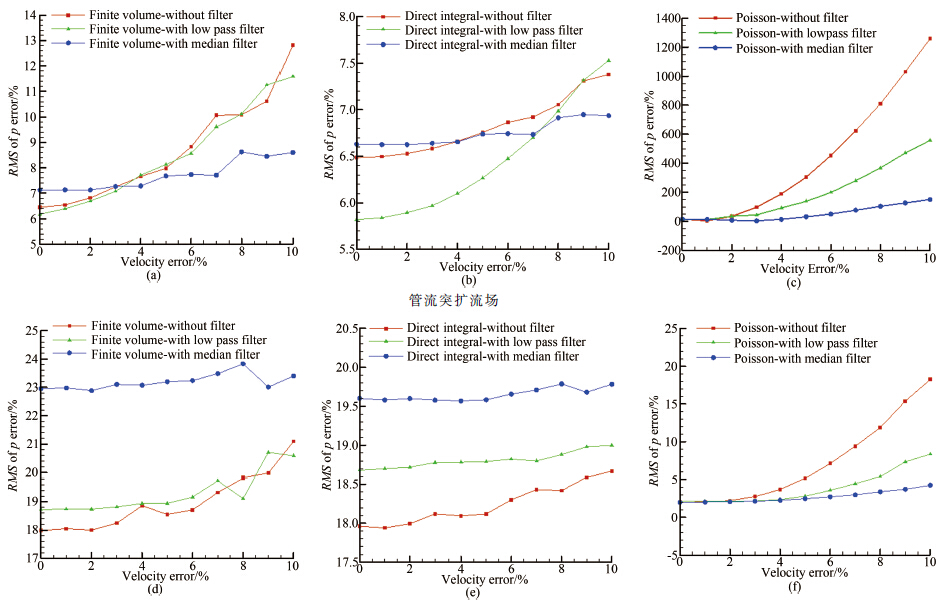
3.2 速度场误差对重构压力场的影响PIV速度场的精度对最终的重构压力场而言至关重要。针对管流突扩流场第40ms的模拟PIV速度场和偏置方块绕流流场第0.5s的模拟PIV速度场,分别加入1%至10%的正态分布误差,采用不同的压力场重构算法,得到相应的重构压力场误差的均方根值,其中PIV查问区边长取0.5mm。为了降低速度场的误差对重构压力场精度的影响,分别采用低通滤波器和中值滤波器对速度场进行滤波处理,并与未进行滤波处理的重构压力场比较,结果如图 11所示。
|
| 图 11重构压力场误差与速度场误差的关系 Fig.11Relationship between the error of reconstructed pressure fields and velocity fields |
可以发现,重构压力场的精度随着速度场误差的增加而逐渐降低。随着PIV速度场误差从1%增加至10%,针对管流突扩流场,有限容积法和直接积分法获得的重构压力场误差的均方根值分别由6.54%和6.49%上升至12.82%和7.38%;针对偏置方块绕流流场,其误差的均方根值分别由18.05%和17.94%上升至21.10%和18.67%。对于Poisson方程法,随着PIV速度场误差从1%增加至10%,管流突扩流场和偏置方块绕流流场的重构压力场误差的均方根值分别由3.62%和2.04%上升至1258.32%和18.25%。相对于Poisson方程法而言,有限容积法和直接积分法具有较强的阻止速度场误差传播的能力,重构压力场误差的变化范围较小,而Poisson方程法重构的压力场误差随着速度场精度的降低迅速增加。但是,对于高精度PIV速度场而言,Poisson方程法重构的压力场精度要高于有限容积法和直接积分法。
为了减少PIV速度场误差对重构压力场精度的影响,预先使用适当的滤波器对速度场进行滤波处理,可以在一定程度上提高重构压力场的精度。对于管流突扩流场而言,采用低通滤波器可以显著提高直接积分法和Poisson方程法的重构精度,但是对于有限容积法的作用不明显;采用中值滤波器可以显著降低有限容积法在较低速度场精度下的重构压力场误差,同时大幅提高了Poisson方程法的重构压力场精度且效果优于低通滤波器,但是对于直接积分法的作用不明显。对于偏置方块绕流流场而言,采用低通滤波器可以显著降低Poisson方程法在较低速度场精度下的重构压力场误差,但是对于有限容积法的作用不明显,对于直接积分法反而增大了重构压力场的误差;采用中值滤波器可以大幅提高Poisson方程法的重构压力场精度且效果优于低通滤波器,但是对于有限容积法和直接积分法而言反倒增大了重构压力场的误差。
总之,对于不同的流场条件,重构算法以及相应滤波方法的选择都是不同的。对于精度较高的PIV速度场,通过采用中值滤波器进行预处理,Poisson方程法的优势较为明显。对于精度较差的PIV速度场,有限容积法和直接积分法可以在较大的速度场误差范围内保持较高的重构压力场精度。
3.3 空间分辨率及插值算法对重构压力场的影响PIV速度场的空间分辨率,即查问区的尺寸对重构压力场精度的影响也很大。同时,在相同的查问区尺寸下,不同的插值算法对重构压力场的误差也有很大影响。
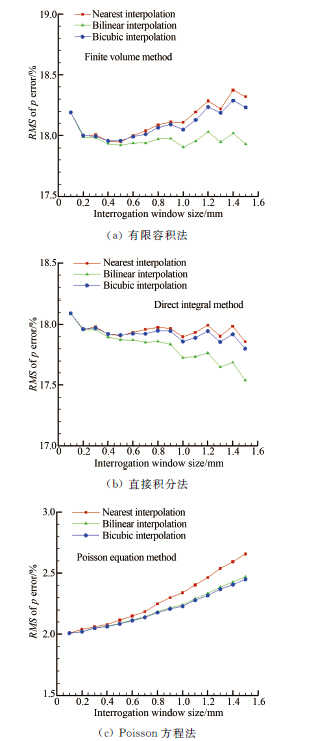
针对偏置方块绕流流场,给定速度场误差为1%,随着PIV查问区边长从0.1mm增大至1.5mm,分别采用最近邻插值(Nearest Interpolation)、双线性插值(Bilinear Interpolation)和双三次插值(Bicubic Interpolation),得到相应重构压力场误差的均方根值,如图 12所示。
|
| 图 12重构压力场误差与插值算法的关系 Fig.12Relationship between the error of reconstructed pressure fields and interpolation algorithms |
可以发现,随着PIV空间分辨率的下降,即查问区尺寸的增大,3种压力场重构算法在不同的插值方式下得到的压力场误差几乎都在增加,其中Poisson方程法下重构压力场误差的增加呈越来越快的趋势。在有限容积法和直接积分法下,双线性插值的精度最高,双三次差值的精度次之,其中,在直接积分法中,双线性插值下的重构压力场误差在一定程度上甚至随着查问区尺寸的增大而减小。在Poisson方程法下,双三次插值算法略好于双线性插值。但是,在上述3种重构算法中,最近邻插值的误差始终最大,因此在实验中不宜采用。
3.4 边界条件的类型对重构压力场的影响在基于PIV速度场重构压力场的过程中,边界条件的类型对重构压力场精度的影响同样十分关键。针对管流突扩第40ms的流场和偏置方块绕流第0.5s的流场,给定速度场误差为1%,分别采用狄利克雷边界条件、诺依曼边界条件和混合边界条件,使用不同的重构算法得到相应的重构压力场,其误差大小如表 1、2所示,PIV查问区边长取0.5mm。其中,混合边界条件介于狄利克雷边界条件和诺依曼边界条件之间,即运用传统测压设备测定PIV测量区域边界上有限个点的压力值,并在边界上的其他位置使用诺依曼边界条件。这种边界条件的目的是在获得一定精度重构压力场的前提下,尽可能地减少压力测点的数量,从而降低实验成本。
| 重构算法 | 管流突扩流场 | ||
| 狄利克雷 | 诺依曼 | 混合 | |
| 有限容积法 | 0.0654 | 0.2393 | 0.0954 |
| 直接积分法 | 0.0649 | 0.29 | 0.1418 |
| Poisson方程法 | 0.0362 | 0.0928 | 0.0374 |
| 重构算法 | 偏置方块绕流流场 | ||
| 狄利克雷 | 诺依曼 | 混合 | |
| 有限容积法 | 0.1805 | 1.801 | 0.4271 |
| 直接积分法 | 0.1794 | 1.7894 | 0.4862 |
| Poisson方程法 | 0.0204 | 1.5176 | 0.0894 |
其中,对于管流突扩流场,在有限容积法和直接积分法中,混合边界条件仅测定了PIV测量区域下壁面均匀分布的7个点的压力值;在Poisson方程法中,混合边界条件仅测定了PIV测量区域左右边界均匀分布的6个点的压力值。对于偏置方块绕流流场,在有限容积法和直接积分法中,混合边界条件仅测定了PIV测量区域左侧边界上均匀分布的4个点的压力值;在Poisson方程法中,混合边界条件仅测定了PIV测量区域左右边界均匀分布的6个点的压力值。
可以发现,在3种不同的压力场重构算法中,狄利克雷边界条件下的重构压力场始终保持较高的精度,诺依曼边界条件下重构压力场的误差始终最大,而混合边界条件下重构压力场的误差略大于狄利克雷边界条件下的重构压力场,但远远小于诺依曼边界条件下的重构压力场。混合边界条件仅仅测定了边界上有限个点的压力值,就获得了接近狄利克雷边界条件下重构压力场的精度,因此在实际工程应用中具有十分重要的意义。
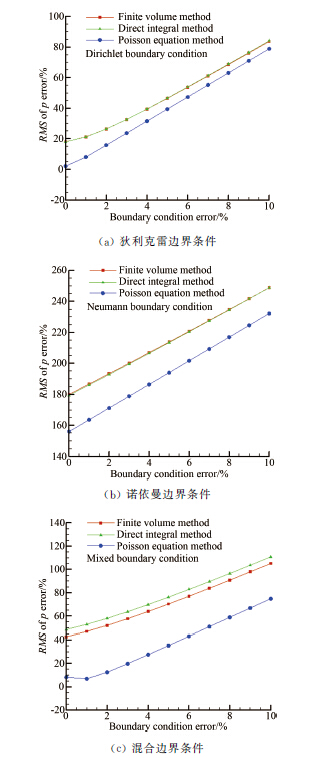
3.5 边界条件的精度对重构压力场的影响边界条件的精度同样显著影响重构压力场的误差。针对偏置方块绕流流场,给定速度场误差为1%,分别采用不同的压力场重构算法和不同类型的边界条件,获得相应的重构压力场,其中PIV查问区边长取0.5mm。随着边界条件的误差从1%上升至10%,重构压力场误差的变化范围如图 13所示。
|
| 图 13重构压力场误差与边界条件误差的关系 Fig.13Relationship between the error of reconstructed pressure fields and boundary conditions |
可以发现,随着边界条件误差的增大,重构压力场的误差几乎呈线性增长,其影响程度甚至比速度场的误差还要大。对于相同类型的边界条件,随着边界条件误差的增加,不同算法下重构压力场的误差几乎以相同的速率增长。因此,精确给定边界条件上的压力值对保证最终的重构压力场精度而言至关重要。
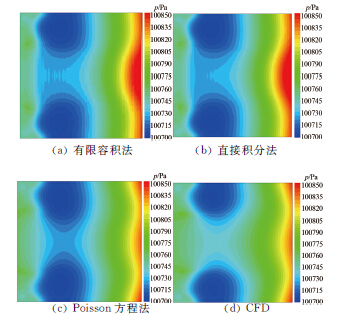
3.6 重构压力场的模拟结果针对管流突扩过程第20ms的流场,加入高斯白噪声,强度为流场平均速度的1%,速度场误差为1%,采用相应的滤波器和合适的插值算法,给定混合边界条件,PIV查问区边长取0.5mm,使用不同的压力场重构算法得到相应的重构压力场,如图 14(a)~(c)所示。CFD模拟得到的压力场如图 14(d)所示。
|
| 图 14管流突扩流场的压力场云图(20ms) Fig.14The pressure contours of the pipe flow (20ms) |
有限容积法、直接积分法和Poisson方程法重构得到的压力场的均方根误差分别为10.62%、10.70%和7.30%。与有限容积法和直接积分法相比,Poisson方程法得到的重构压力场更加光滑,这也验证了Poisson方程本身所具有的低通滤波器特性。
4 结论本文结合CFD数值模拟,通过管流突扩流场和偏置方块绕流流场,验证了3种基于PIV速度场重构压力场算法的正确性和可行性,同时研究了噪声、速度场误差、插值算法以及边界条件的类型和精度对重构结果的影响,得到如下结论:
(1)有限容积法和直接积分法重构的压力场容易受到噪声的影响而产生剧烈震荡,通过使用滤波器预处理可以降低重构压力的震荡,从而提高重构压力场的光滑程度;Poisson方程法不易受噪声的影响而产生震荡,并且采用中值滤波器可以提高重构压力场的精度。
(2)若PIV速度场的精度较高,则Poisson方程法的优势较为突出。对于精度较差的PIV速度场,有限容积法和直接积分法可以在较大的速度场误差范围内保持较高的重构压力场精度。
(3)3种压力场重构算法在不同的插值方式下得到的压力场误差几乎都随PIV空间分辨率的下降而增加。有限容积法和直接积分法采用双线性插值,Poisson方程法采用双三次差值可以获得更高精度的重构压力场。
(4)狄利克雷边界条件下的重构压力场精度最高,诺依曼边界条件最低,混合边界条件仅仅测定边界上有限个点的压力值,就获得了接近狄利克雷边界条件下重构压力场的精度,因此在实际工程应用中具有十分重要的意义。随着边界条件精度的下降,不同算法下的重构压力场误差几乎以相同的速率增长,其影响程度比速度场还要大。因此,精确给定边界上的压力值对保证最终的重构压力场精度而言至关重要。
| [1] | 李丹勋, 曲兆松, 王兴奎, 等. 粒子示踪测速技术原理与应用[M]. 北京: 科学出版社 ,2012 : 1 -15. Li D X, Qu Z S, Wang X K. Principle and application of particle tracing technique[M]. Beijing: Science Press , 2012 : 1 -15. |
| [2] | Henning A, Kaepernick K, Ehrenfried K, et al. Investigation of aeroacoustic noise generation by simultaneous particle image velocimetry and microphone measurements[J]. Experiments in Fluids , 2008, 45 (6) : 1073–1085. DOI:10.1007/s00348-008-0528-y |
| [3] | Larsson J, Davidson L, Olsson M, et al. Aeroacoustic investigation of an open cavity at low Mach number[J]. AIAA Journal , 2004, 42 (12) : 2462–2473. DOI:10.2514/1.1339 |
| [4] | 徐惊雷. PIV技术在超及高超声速流场测量中的研究进展[J]. 力学进展 , 2012 (01) : 81–90. Xu J L. The research progress of PIV in the measurement of ultra-and hypersonic flow fields[J]. Advances in Mechanics , 2012 (01) : 81–90. |
| [5] | 王勇, 陈鹏, 耿子海, 等. 基于PIV速度场测量重构压强场的研究进展[J]. 实验流体力学 , 2014, 04 : 1–8. Wang Y, Chen P, Geng Z H, et al. Development of PIV based instantaneous pressure determination[J]. Journal of Experiments in Fluid Mechanics , 2014, 04 : 1–8. |
| [6] | Gurka R, Liberzon A, Hefetz D, et al. Computation of pressure distribution using PIV velocity data[C]//Workshop on Particle Image Velocimetry, 1999. |
| [7] | Hosokawa S, Moriyama S, Tomiyama A, et al. PIV measurement of pressure distributions about single bubbles[J]. Journal of Nuclear Science and Technology , 2003, 40 (10) : 754–762. DOI:10.1080/18811248.2003.9715416 |
| [8] | Fujisawa N, Nakamura Y, Matsuura F, et al. Pressure field evaluation in microchannel junction flows through μPIV measurement[J]. Microfluidics and Nanofluidics , 2006, 2 (5) : 447–453. DOI:10.1007/s10404-006-0088-5 |
| [9] | Fujisawa N, Tanahashi S, Srinivas K. Evaluation of pressure field and fluid forces on a circular cylinder with and without rotational oscillation using velocity data from PIV measurement[J]. Measurement Science and Technology , 2005, 16 (4) : 989. DOI:10.1088/0957-0233/16/4/011 |
| [10] | Van Oudheusden B W. Principles and application of velocimetry based planar pressure imaging in compressible flows with shocks[J]. Experiments in Fluids , 2008, 45 (4) : 657–674. DOI:10.1007/s00348-008-0546-9 |
| [11] | Van Oudheusden B W, Scarano F, Roosenboom E W M, et al. Evaluation of integral forces and pressure fields from planar velocimetry data for incompressible andcompressible flows[J]. Experiments in Fluids , 2007, 43 (2-3) : 153–162. DOI:10.1007/s00348-007-0261-y |
| [12] | Charonko J J, King C V, Smith B L, et al. Assessment of pressure field calculations from particle image velocimetry measurements[J]. Measurement Science and Technology , 2010, 21 (10) : 105401. DOI:10.1088/0957-0233/21/10/105401 |
| [13] | De Kat R, Van Oudheusden B W, Scarano F. Instantaneous planar pressure field determination around a square-section cylinder based on time resolved stereo-PIV [C]//Proceedings of the 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Posrtugal, 2008. |
| [14] | De Kat R, Van Oudheusden B W, Scarano F. Instantaneous planar pressure field determination around a square-section cylinder based on time resolved stereo-PIV [C]//Proceedings of the 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Posrtugal, 2008. |
| [15] | De Kat R, Van Oudheusden B W. Instantaneous planar pressure determination from PIV in turbulent flow[J]. Experiments in Fluids , 2012, 52 (5) : 1089–1106. DOI:10.1007/s00348-011-1237-5 |
| [16] | De Kat R, Van Oudheusden B W. Instantaneous planar pressure from PIV: analytic and experimental[3] test-cases[C]//Proceedings of the 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 2010. |
| [17] | Adrian R J. Twenty years of particle image velocimetry[J]. Experiments in Fluids , 2005, 39 (2) : 159–169. DOI:10.1007/s00348-005-0991-7 |
| [18] | Raff M, Willert C, Wereley S, et al. Particle image velocimetry: a practical guide[M]. 2nd ed. Berlin: Springer-Verlag: , 2007 . |
| [19] | 马静. 超燃冲压发动机内流通道冷态流场的PIV试验研究[D]. 南京: 南京航空航天大学, 2010. Ma J. PIV experiment study of scramjet internal cold flow field[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2010. |
| [20] | 林春峰. 超声速冲击射流的PIV实验研究[D]. 南京: 南京航空航天大学, 2006. Lin C F. A PIV study of supersonic impinging jet[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2006. |
| [21] | 王大伟, 王元. 由PIV的速度场获取压强分布的数值方法. 北京: 中国科技论文在线. http://www.paper.edu.cn/releasepaper/content/200611-227. Wang D W, Wang Y. A numerical method for obtaining the pressure distribution of the velocity field by PIV. Beijing: Science Paper Online. http://www.paper.edu.cn/releasepaper/content/200611-227. |
| [22] | Van Oudheusden B W. PIV-based pressure measurement[J]. Measurement Science and Technology , 2013, 24 (3) : 032001. DOI:10.1088/0957-0233/24/3/032001 |
| [23] | 周正贵, 等. 计算流体力学基础理论与实际应用[M]. 南京: 东南大学出版社 ,2008 . Zhou Z G, et al. Basic theories and practical applications of computational fluid dynamics[M]. Nanjing: Southeast University Press , 2008 . |
| [24] | Baur T, Köngeter J. PIV with high temporal resolution for the determination of local pressure reductions from coherent turbulence phenomena[C]//3rd International Workshop on Particle Image Velocimetry, Santa Barbara, CA, USA, 1999. |