2. 航天科工集团二院, 北京 100854
2. The Secnod Academy, China Aerospace Science&Industry Corporation, Beijing 100854, China
超高速飞行器壳体温度测量与分析是飞行器光辐射特性研究、飞行器防热设计的重要内容。由于超高速飞行器属于壳体结构,飞行环境、飞行参数随飞行时间变化大,造成飞行器壳体温度呈现非均匀分布和动态变化特点。对于飞行器壳体温度,一般采用接触方式测量。有关介绍飞行器气动热、热传导与壳体温度的计算方法[1-10]和接触式测温方法[11-13]的文章非常多,计算方法主要针对飞行器气动热、热传导和表面温度分布,重点关注于飞行器气动热的分析和在气动热作用下的温度分析,少有考虑在没有气动热作用后(飞行中段)的表面温度变化过程,也鲜有与飞行中段实际飞行测量数据的比较。准确测量飞行中段飞行器表面温度对于验证飞行器飞行中段红外辐射特性分析数据的可靠性具有十分重要的意义。而温度测量主要关注探测器应用、探测器结构本身对测量温度的影响和误差分析等,未见有对出现逆向传热时探测器安装结构对测点温度影响的研究报道。
本文针对薄壁结构飞行器在有正向传热和逆向传热过程时的温度测量探测器安装结构是否会对测点温度造成影响、探测器测量温度是否能真实反映未装探测器时测点位置的温度这一问题,采用气动热工程算法与热传导计算方法对探测器安装结构对测点温度的影响进行了分析,并与飞行实验测量结果进行了对比,得出了某飞行实验采用的探测器安装结构对于飞行器壳体测点位置温度存在影响这一结论,并提出了针对其壳体结构采用相应的探测器安装结构来减小对测点温度影响的方案。
1 计算方法 1.1 气动热计算方法飞行器气动热采用工程算法进行计算。 飞行器在马赫数不大于1.5时的气动热qw采用亚、跨声速气动加热热流公式[3]计算。马赫数大于1.5时的气动热计算方法如下:自由分子流区气动加热热流qfm采用文献[4]中公式计算;在稀薄过渡流区,气动加热热流qbr采用Linear函数[5]计算;对于连续流区物面气动热,驻点热流qs采用Fay-Riddell公式[6]计算;层流区各点热流qwl采用Lees修正公式[7]计算;湍流区各点气动热热流qwt采用平板参考焓法[8]计算;转捩区热流qwtr采用加权平均法[9]计算。转捩准则为:转捩起始点位置采用局部马赫数相关的转捩准则(简称“72-90”准则)[10]确定。
1.2 飞行器吸收的太阳辐射热流计算方法飞行器在飞行过程中,阳光照射面会吸收太阳辐射。假定太阳光为均匀的平行光束,飞行器微元表面吸收的太阳直接辐射热流qSun为:
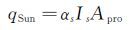
式中:αs为飞行器器表面的太阳辐射吸收率;Is为太阳直接辐射照度;Apro为单位微元表面在垂直于太阳光方向上的投影面积。
由于地球绕太阳的运行轨道为椭圆形,地球在轨位置不同时,大气层外的太阳直接辐射通过对太阳常数进行日地距离修正:
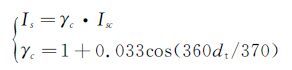
式中:dt为试验当天距离本年1月1日的天数,Isc=1353W/m2为太阳常数。
1.3 飞行器吸收的地球辐射热流计算方法地球是一个以红外辐射为主的辐射体,其辐射同样会被飞行器吸收。假设地球表面各处的辐射强度相等,则飞行器微元表面吸收的地球辐射热流qEarth为:
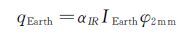
式中:αIR为飞行器外表面的红外吸收率,IEarth为地球自身的红外辐射强度,φ2mm为地球红外辐射的角系数。
1.4 飞行器吸收地球反射太阳辐射热流计算方法假定地球对太阳辐射的反射为漫反射,遵循Lambert定律,并且各处均匀,反射光谱与太阳光谱一致,地球反射率取全球平均反射率0.35,飞行器微元表面吸收的地球反射太阳辐射的热流qref为:
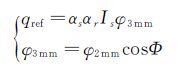
式中:αr为地球表面对太阳辐射的平均反射率,φ3mm地球反照角系数,Φ为地球反照角。
1.5 飞行器向外辐射的辐射热流计算方法飞行器通常可认为是灰体,其表面向外辐射的热流采用灰体辐射公式计算。
1.6 温度场计算方法飞行器受太阳辐射加热、地球辐射与地球反射太阳辐射加热及在大气层内的气动加热升温和因热辐射和热传导降温,涉及正、逆向动态传热问题。在温度场计算中,将工程计算所得热环境数据进行变换,引入等量对流换热系数。以数据文件给出不同时刻的等量换热系数,进而以数组参数形式读入作为施加气动加热的对流边界条件,同时考虑物体对外的辐射冷却效应,在外边界上施加辐射边界条件,内壁组成封闭腔室结构。
飞行器壳体温度场采用有限元方法对结构温度场变化历程进行计算。
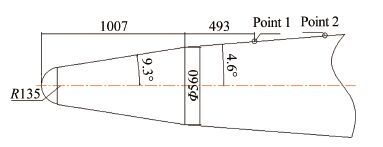
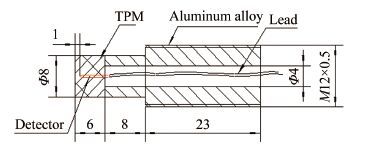
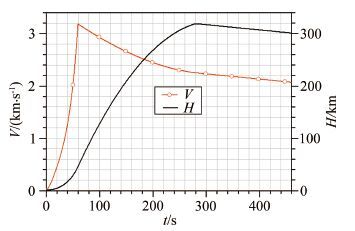
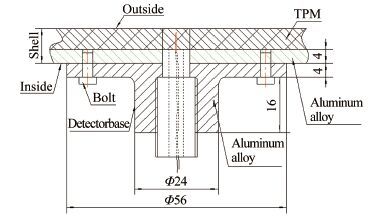
2 参数条件与测量数据在某飞行器飞行试验中,在飞行器壳体(局部外形如图 1所示,由防热层材料(Thermal Protection Material,简称TPM)和铝合金构成)典型位置安装了结构如图 2所示的测温探测器,测量了飞行器按图 3所示弹道飞行时壳体2典型位置(测点1与头部距离为1500mm,测点2与头部距离为2000mm)表面下1mm处的温度变化历程,探测器安装结构如图 4所示。
|
| 图 1飞行器局部简化外形(单位:mm) Fig.1Partial sketch of flying target(unit:mm) |
|
| 图 2原测温探测器简化结构(单位:mm) Fig.2Sketch of original detector(unit:mm) |
|
| 图 3飞行器弹道参数 Fig.3Ballistic trajectory |
|
| 图 4原测温探测器安装结构 Fig.4Installing structure sketch of original detector |
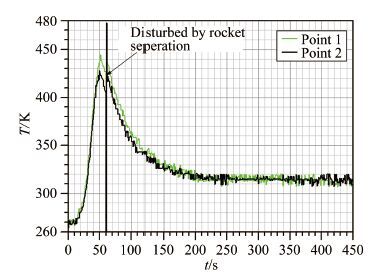
图 5给出了飞行器从发射开始后2个典型测点 的温度变化历程,包括了在大气层内飞行时的升温阶段和在大气层外的降温阶段(剧烈跳动区域是由于发动机分离震动造成,该区域数据无效)。
|
| 图 5测量温度随时间的变化曲线 Fig.5Measured temperature curves |
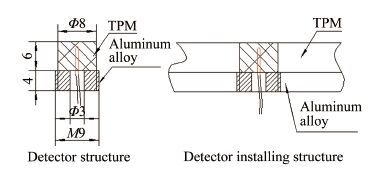
图 6是本文结合飞行器壳体结构和温度变化特性提出的改进探测器结构及安装结构示意图。
|
| 图 6改进测温探测器结构及安装方案 Fig.6Reformed detector structure and installing structure |
| 红外发射率 | 密度/(kg·m-3) | 导热系数/(W·(m·K)-1) | 比热/(J·(kg·K)-1) |
| 0.85 | 1750 | 0.44 | 1000 |
| 温度/K | 298 | 373 | 423 | 473 | 523 | 573 |
| 比热/(J·(kg-1·K)-1) | 921 | 921 | 1005 | 1047 | 1089 | 1089 |
| 密度/(kg·m-3) | 2640 | |||||
| 导热系数/(W·(m·K)-1) | 125.6 | |||||
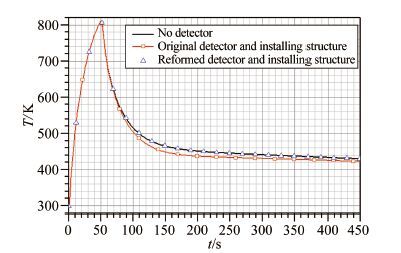
针对未安装测温探测器壳体结构、安装原测温探测器壳体结构(如图 4所示)与安装改进后的测温探测器壳体结构(如图 6所示),对其防热材料表面以100kW/m2的热流进行加热50s(初温300K),然后辐射冷却至450s,分析了表面下1mm处位置(即探测器表面所处位置)的温度时间历程,如图 7所示。
|
| 图 7测点计算温度随时间的变化曲线 Fig.7Time variation of calculated temperatures at measured point |
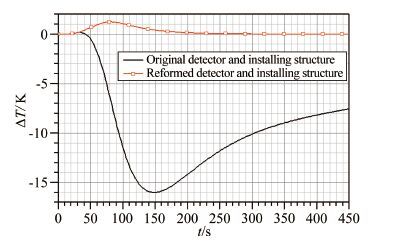
从图 7中可以看出:前50s的加热阶段和辐射与热传导降温初期阶段,特别是前50s的加热阶段,2种测温探测器结构及安装方案对测点位置温度影响较小;而后,测点温度受探测器及安装结构影响,原测温探测器结构及安装结构对测点温度影响明显,主要时间段内测量温度会低于不装探测器时测点位置的温度,最大差值达到16K,到400s时,差值还有-8K(如图 8所示);而采用改进后的测温探测器结构及安装结构,虽然测量温度在一个较短时段会略高于不装探测器时测点位置的温度,但最大差值不到2K,100s后,相对偏差不超过2‰。也就是说,原测温探测器结构及安装结构不能完全真实反映表面下1mm位置的温度,在表面处于降温阶段,测量温度明显低于真实温度;而改进后的测温探测器结构及安装结构基本可以真实反映表面下1mm位置的温度。
|
| 图 8不同探测器结构及安装结构造成的测点温差 Fig.8 Temperature errors made by different detectors and installing structures |
产生上述现象的原因是:原测温探测器安装方案中增加了厚度远大于壳体内层铝合金的铝合金安装座且探测器铝合金安装杆远大于壳体内层铝合金厚度,而铝合金导热系数远高于防热材料,当热量由防热材料传导到铝合金时,热量将被迅速传导到整个铝合金上,尽管穿线孔的存在会减小热量的吸收,但穿线孔体积远小于增加的铝合金安装座和铝合金安装杆体积,总体效果看,相较于不安装探测器时,附加的铝合金安装座和铝合金安装杆要吸收更多热量,必然引起测点温度下降,致使测量温度不能真实反映不装探测器时测点位置的温度;而采用改进测温探测器结构和安装方案,基本不改变壳体结构,只是由于穿线孔的存在减小了吸热会使测点的温度有所增加,而穿线孔体积很小,该孔体积大小的铝合金热容量也很小,对测点温度影响并不会十分明显,如果穿线孔更小,其对测点温度的影响将更小。
针对实际飞行情况,首先计算分析了飞行器外表面的气动热,然后,利用该热流值并考虑热辐射、热传导影响,对未安装测温探测器的壳体结构、安装原测温探测器的壳体结构(如图 4所示)与安装改进后的测温探测器的壳体结构(如图 6所示)测点位置的温度变化历程进行了计算分析。
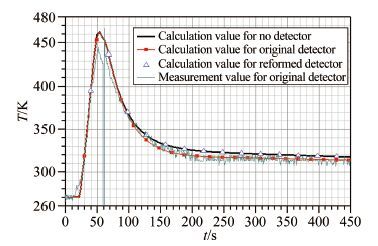
图 9和10是图 1所示飞行器在图 3所示飞行弹道条件下测点1和2处计算温度与按原探测器结构及安装结构测量得到的温度的对比。
|
| 图 9测点1计算温度与飞行试验测量温度对比 Fig.9Comparison of temperatures at measured point 1 |
|
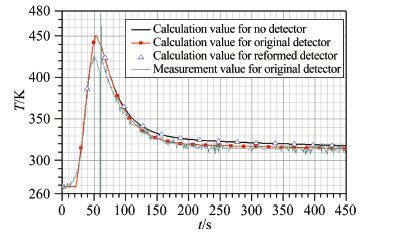
| 图 10测点2计算温度与飞行试验测量温度对比 Fig.10Comparison of temperatures at measured point 2 |
从图 9和10可以看出:飞行器在有气动加热、其表面处于升温过程或热量由壳体表面向内部传导时,安装测温探测器对测点位置温度影响较小,测温探测器测量到的温度可反映不装探测器时测点位置温度;但当飞行器表面由于辐射散热、表面温度低于壳体内部温度造成热量由壳体内部向外表面传导时,原探测器及安装结构对测点温度影响明显,测量温度低于不装探测器时测点位置的温度;而按原探测器结构及安装方案,计算得到的测点位置温度与实际测量温度基本一致,特别是在最为关心200~450s时间段(即飞行中段)内,计算温度曲线基本处于测量温度曲线波动范围,一方面说明了计算方法是可信的,另一方面说明原探测器结构与安装方案对飞行中段飞行器测点温度确实会造成影响;按改进后的测温探测器结构及安装方案,测点位置计算温度与不装探测器时测点位置计算温度一致,说明改进后的探测器结构及安装方案可真实反映测点位置温度。
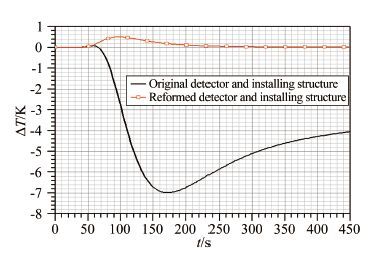
图 11和12给出了飞行器测点1和2按原探测器结构及安装结构和按改进结构计算得到的温度与不安装探测器时计算得到的温差比较。
|
| 图 11不同探测器及安装结构对测点1温度影响 Fig.11 Temperature errors made by different detectors and installing structures at measured point 1 |
|
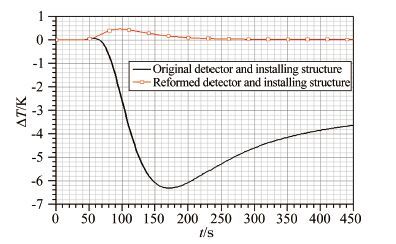
| 图 12不同探测器及安装结构对测点2温度影响 Fig.12 Temperature errors made by different detectors and installing structures at measured point 2 |
从中可以看出:飞行器测点1和2按原探测器结构及安装结构计算得到的温度会普遍低于不装探测器时的计算温度,最大温差达到7K,在最为关心的200~450s时间段,最小温差也大于3.5K;而按改进后的探测器结构及安装结构,计算得到的因探测器安装带来的温差在整个测量时间段都不大于0.5K。
4 结 论通过计算分析与对比,可得到以下结论:
(1) 飞行器在有气动加热、其表面处于升温过程或热量由壳体表面向内部传导时,测温探测器结构及安装结构对测点温度无影响。
(2) 当飞行器表面在辐射散热、表面温度低于壳体内部温度造成热量由壳体内部向外表面传导时,测点温度会受探测器结构及安装结构影响,原探测器结构及安装结构使得测量温度明显低于不装探测器时的温度。
(3) 本文针对薄壁结构飞行器表面温度变化历程测量要求改进的测温探测器结构及安装方案对飞行器飞行中段测点温度基本无影响。
| [1] | 陈鑫, 刘莉, 李昱霖, 等. 高超声速飞行器翼面气动加热、辐射换热与瞬态热传导的耦合分析[J]. 弹道学报 , 2014, 26 (2) : 1–5. Chen X, Liu L, Li Y L, et al. Coupled study of aerodynamic heating, radiative heat transfer and heat conduction for airfoils of hypersonic vehicles[J]. Journal of Ballistics , 2014, 26 (2) : 1–5. |
| [2] | 杨荣, 王强. 高超声速旋转体气动加热、辐射换热与结构热传导的耦合数值分析[J]. 上海航天 , 2009 (4) : 25–29. Yang R, Wang Q. Coupled numerical study on aero-heating, radiative heat transfer and structure heat conduction for hypersonic bodies of revolution[J]. Aerospace Shanghai , 2009 (4) : 25–29. |
| [3] | 王政. 飞机机翼热控方案研究及热管传热特性分析[D]. 南京: 南京航空航天大学, 2009. Wang Z. Study on thermal control scheme of aircraft wing and analysis of heat transfer characteristics of heat pipe[D]. Nanjing: Nanjing University of Aeronautics&Astronautics, 2009. |
| [4] | Engel C D. Miniver upgrade for the avid system, Vol.1: Lanmin user's manual[R]. NASA CR-172212, 1983. |
| [5] | 戎宜生, 刘伟强. 过渡流区钝锥体Linear桥函数调节参数研究[J]. 物理学报 , 2012, 64 (4) : 1–5. Rong Y S, Liu W Q. Research on accommodation parameter of linear bridging relation for blunt cone in transitional regime[J]. Acta Physica Sinica , 2012, 64 (4) : 1–5. |
| [6] | Fay J A, Riddell F R. Theory of stagnation point heat transfer in dissociated air[J]. J Aero Sci , 1958, 25 (2) : 73–85. DOI:10.2514/8.7517 |
| [7] | Lees L. Laminar heat transfer over blunt nosed bodies at hypersonic flight speed[J]. Jet Propulsion , 1956, 26 (4) : 259–269. DOI:10.2514/8.6977 |
| [8] | 张志成, 潘梅林, 刘初平, 等. 高超声速气动热和热防护[M]. 北京: 国防工业出版社 ,2003 . Zhang Z C, Pan M L, Liu C P, et al. Hypersonic heating and thermal protection[M]. Beijing: Defense Industry Press , 2003 . |
| [9] | Chen K K. Three dimensional nosetip shape changes in hypersonic flow. Part 1: Illustration of a mathematical model-characteristic method[R]. AIAA-73-0762, 1973. |
| [10] | Baker R L. Low temperature ablator nosetip shape change at angle of attack[R]. AIAA-72-90, 1972. |
| [11] | 王友良, 孙新川, 程相飞. 飞机机身结构温度测量[J]. 飞行试验 , 2003, 19 (2) : 15–17. Wang Y L, Sun X C, Cheng X F. Aircraft fuselage structural temperature measurement[J]. Aviation Experiment , 2003, 19 (2) : 15–17. |
| [12] | 北京航空航天大学. 碳纤维复合材料高速飞行器整流罩表面瞬态温度测量装置: 中国, CN200610113792.9[P]. 2006-10-11 Beijing University of Aeronautics&Astronautics. Surface temperature measuring apparatus for high speed vehicle fairing made by carbon fiber composite material: China, CN200610113792.9[P]. 2006-10-11. |
| [13] | 徐顺生, 时章明, 杨刚. 基于传热原理的热电偶测温误差模型及应用[J]. 传感器与微系统 , 2006, 25 (5) : 15–17. Xu S S, Shi Z M, Yang G. Error model and application of temperature measure about thermo-couple based on heat transfer principle[J]. Transducer and Micro System Technologies , 2006, 25 (5) : 15–17. |



