面积律的发现源于R. T. 惠特科姆于1952年所进行的风洞实验,根据实验的现象,惠特科姆提出了跨声速面积律,而后在理论上经过旋成体的小扰动线化理论分析得到证明[1-2]。
面积律作为上世纪50年代空气动力学领域最伟大的发现之一,有力地推动了航空科学技术的发展,成功地使飞机的飞行跨越了声速,此后各种以跨声速或者超声速飞行的飞行器的设计、研制,无一不遵循面积律的原则[3-4]。
但是跨声速面积律的理论证明是基于小扰动线性化假设条件下完成的,隐藏在面积律背后的流动机理却一直没有得到很明确的研究和阐述,造成面积律的描述过于定性,在某些情况下给实际的飞机设计工作带来了一定的困惑和问题。
另一方面,现在及未来飞机设计的要求在不断提高,气动力设计手段也从小扰动理论提升为CFD方法,空气动力学设计朝着越来越精细化的方向发展,对于流场和流动现象的分析越来越细致[5-7]。相比较而言,建立在小扰动理论基础上的面积律在设计空气动力学迅速发展的今天则略显“粗糙”[8],在对未来飞行器气动布局及外形设计的研究中逐渐显露其指导性略显不足的问题[9-12]。为此一些研究者转而试图采用优化等方法解决跨声速、超声速设计方案的减阻问题[13-19];同时另外一些研究者则试图从理论角度探讨波阻的减小方法[20-26]。
本文的研究从跨声速面积律出发,结合CFD方法和优化方法,分析面积律减阻的流动机理,寻找面积律的本质,探讨面积律在更深和更精细的层次上对飞机设计的指导原则。同时探索利用CFD方法分析和解释风洞试验中发现的试验现象,结合试验和CFD方法总结相关规律和法则,并应用于指导飞机的设计与优化。
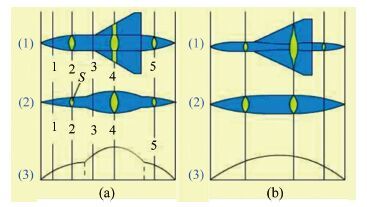
1 经典面积律及其应用跨声速面积律描述为:当飞行马赫数接近于1时,为了使波阻最小,飞行器所有部件的横截面积叠加在一起的分布应该相当于一个当量旋成体横截面积的分布,或者分布曲线比较光滑而无不规则的变化。如图 1所示,(1)为实际飞行器,(2)为当量旋成体,(3)为实际飞行器和当量旋成体的横截面积分布曲线,(a)为不满足跨声速面积律的面积分布形式,(b)为满足跨声速面积律的面积分布形式。
|
| 图 1跨声速面积律 Fig.1Transonic area law |
面积律的描述简单,很快即被应用于飞机设计实践。美国的YF-102战斗机在1954年试飞时由于跨声速波阻过大而未超过声速,后来通过其改型YF- 102A的机身蜂腰设计达到了跨声速面积律所需要的横截面积分布,同年试飞时顺利地突破音障,成为第一架采用面积律设计的飞行器。其后世界上各种以接近声速或者超声速飞行的飞行器无一不应用面积律设计。
2 面积律设计中的问题面积律自提出后很快被成功应用于飞机设计,但是经由实验现象总结、仅在小扰动线性化范围内推导而得的面积律只有定性的阐述和粗略的定量描述,因此在飞机设计实践中也给设计人员造成了一些困惑,带来了一些困难。
首先,面积律未能给出其减阻的流动近场机理。近场机理的缺失使得应用面积律进行气动外形设计的过程显得过于“粗犷”,不利于精细化的气动力设计,不易获得最优的减阻效果。
其次,根据实验结果总结和小扰动线化理论推导的面积律仅适用于细长体,而对于非细长体如何降低其波阻则没有直接指导意义。
第三,面积律要求横截面积分布曲线光滑,在实际工程中常用的外形修形方式是形如图 1(b)所示的收缩机身形成蜂腰。蜂腰减小中机身截面积将严重影响中机身的容积,而中机身又是容纳飞机燃油、有效载荷等装载的最佳场所。这样对于其他一些飞机功能需求而言则是非常不利的。
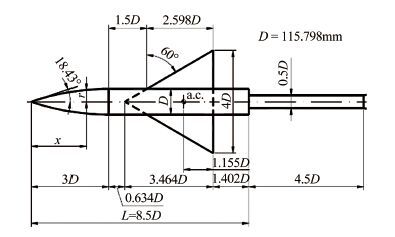
3 研究方法为了获得面积律减阻的近场机理,本文选用了具有明确的参数化外形描述的AGARD-B标模[27],如图 2所示。该标模外形简单,其主要参数如表 1所示,AGARG-B标模具备典型的高速飞行器外形特征,用于研究面积律非常合适。
|
| 图 2AGARD-B标准模型参数化外形定义 Fig.2Parameter definitions of standard model AGARD-B |
| 参数 | 值 |
| 参考面积 | 0.0929m2 |
| 机翼前缘后掠角 | 60° |
| 机翼展弦比 | 2.31 |
| 机翼相对厚度 | 4% |
| 机身长细比 | 8.5 |
| 机头长细比 | 3 |
| 翼型 | 双圆弧翼型 |
| 翼型最大厚度位置 | 50%弦长 |
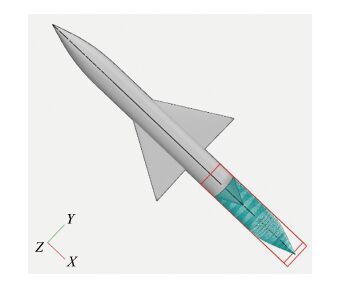
实际采用的计算数模如图 3所示,模型尾部增加了收缩尾锥(但在结果积分时不考虑这一段的贡献)。同时为了简化分析过程,主要针对马赫数等于1.0、迎角为0°的状态进行分析研究,最后结合跨声速飞行的典型升力系数状态进行验证。
|
| 图 3CFD计算采用的几何数模 Fig.3Geometry model for CFD computation |
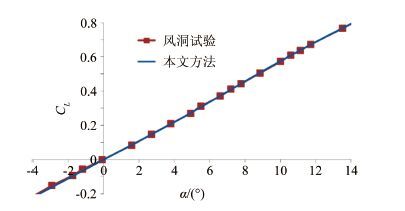
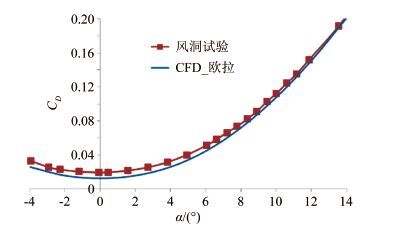
由于面积律减阻的对象是波阻,因此在算法方面本文选择了欧拉方法,在获得本文分析所需的足够计算精度的同时,避免RANS方法需要的巨大计算资源和时间。马赫数1.0时,AGARD-B标模试验数据的与本文所采用的CFD方法计算结果的升力、阻力对比情况分别如图 4和5所示。升力的计算结果与试验完全吻合,阻力的计算结果较试验略小,二者之间的差量为摩擦阻力,不影响本文对于面积律减小激波阻力的分析。
|
| 图 4本文方法计算的升力与试验结果的对比 Fig.4Lift comparison between test and computation |
|
| 图 5本文方法计算的阻力与试验结果的对比 Fig.5Drag comparison between test and computation |
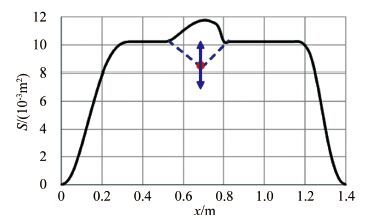
迎角0°时,计算数模的横截面积分布如图 6所示。

|
| 图 6计算数模横截面积分布 Fig.6Cross section distribution of geometry model |
按照经典的跨声速面积律的要求,欲使波阻最小,需要横截面积分布如同图中黑色虚线所示,而由于机翼的存在,面积分布出现一个鼓包。因此在保持机翼不变的情况下,必须缩小机翼所在位置机身的直径,使得此处单独机身的横截面积分布出现如同图中红色虚线所示的“凹坑”。为了简化问题的复杂程度,“凹坑”深度初值取机翼最大横截面积,在“凹坑”最低点与机翼外露根弦前后缘之间,机身横截面积线性变化,形成图 6中虚线围成的机身修形三角区,对应的CFD分析数模如图 7所示。

|
| 图 7面积律修形后的计算数模 Fig.7Geometry model modified with transonic area law |
基于前文的设定,采用优化设计的自动程序,首先固定修形三角区下顶点高度坐标,搜索阻力最小的轴向位置(以下简称第1种搜索),然后将下顶点固定在最佳轴向位置,搜索阻力最小的法向位置(以下简称第2种搜索),从而得到机身修形的最佳方案,与跨声速面积律结果进行对比分析,探讨跨声速面积律减阻的近场流动机理。
4 面积律的近场流动分析 4.1 机身修形方式对减阻效果的影响为了研究机身收缩程度以及最大收缩位置对于减阻效果的影响,分析过程中改变了一系列机身最大收缩直径及其纵向位置(沿机身轴线方向)进行了优化计算。
首先根据AGARD-B标模的最大横截面积,按照图 6黑色虚线所示的面积律要求确定机身轴对称最大收缩直径(最大收缩面积),采用第1种搜索方式,经过CFD计算之后得出相对应的一系列阻力值,拟合之后得到阻力随机身轴对称最大收缩位置之间的变化关系,如图 8所示。

|
| 图 8阻力随机身最大收缩直径所在位置的变化 Fig.8 Drag varies with fuselage location of maximum contraction diameter |
由此可见,随着收缩机身最小直径所在机身轴线位置从机翼安装根弦前缘向后缘的移动,机身修形之后的阻力值逐渐减小,直到某个位置阻力达到最小值,与修形前的等直机身相比,阻力减小约0.0041;而后随着最大收缩直径位置的继续后移,阻力值则不降反升。
需要注意的是,由图 8的阻力变化规律可以发现一个经典面积律未能给出的现象,即:机身按照面积律原则进行横截面积收缩时,收缩最大的最优位置并不位于机翼导致的横截面积增量最大的位置(如图 8中红色竖线所示位置),而在于该位置之后的某处。相对于在横截面积增量最大位置进行的最大收缩构型,图 8给出的最优收缩构型还能获得额外的约33%(约0.001)的减阻收益。由此可以得出结论,在应用面积律对飞行器进行跨声速减阻设计时,如果将机身横截面积最大收缩位置对应至原始横截面积分布最突出位置的话,此时未必能获得最佳的减阻效果。为了达到最佳的减阻效果,需要通过优化设计的方法寻找合适的机身最大收缩位置。
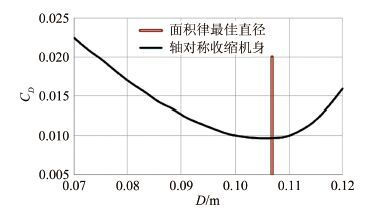
接下来使用第2种搜索方式研究横截面积收缩程度对减阻效果的影响。如图 9所示,可以获得相应的减阻效果如图 10所示。
|
| 图 9改变机身最大收缩直径的计算数模横截面积分布 Fig.9 Cross section distribution of geometry model for changing fuselage maximum reducing diameter |
|
| 图 10不同机身最大收缩直径对减阻效果的影响 Fig.10 Drag reduction with various minimal fuselage diameter after contraction |
图 10中的红色竖线表示之前按照面积律原则确定的机身最大收缩直径,由图可见,在此直径附近的阻力变化趋势趋平,远离此直径时则阻力急剧增大。因此面积律所确定的机身最大修形面积可以获得最好的减阻效果,同时在该面积值附近,减阻效果对于横截面积的变化并不敏感。
综合图 8和10的结果不难看出,采用优化设计的方法可以获得与跨声速面积律基本一致的结论。但是结合CFD方法的优化方法给出了减阻效果更好的结果,同时还揭示了经典面积律未能描述的现象。
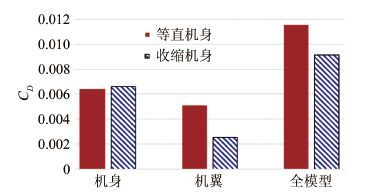
4.2 飞行器各部件对面积律减阻的贡献面积律修形可以使全机获得波阻减小的收益,但经典面积律并未指出收益从何而来。分析上一节优化得到的最优减阻构型,将其阻力按部件进行分解,可以得到如图 11所示的面积律减阻前后各部件阻力贡献对比情况。
|
| 图 11面积律减阻前后各部件阻力贡献对比 Fig.11 Comparison of drag contributions of different components with/without area rule |
按照面积律原则对机身进行收缩修形之后,对于机身而言,所受到的阻力略有增加;对于机翼,则阻力得到大幅度降低;二者叠加,最终获得了全机的阻力减小。由此可见,此例面积律减阻是通过修改机身的外形,在付出机身阻力的轻微代价的情况下,依靠机翼获得的大幅度减阻收益,实现了全机减阻收益。
4.3 面积律减阻的近场流动机理分析根据优化的结果,利用CFD计算所得到的流场数据,可以绘制面积律减阻前后模型表面的阻力分布分别如图 12和13所示。

|
| 图 12等直机身的计算数模阻力分布 Fig.12Drag distribution without area rule |

|
| 图 13收缩机身的计算数模阻力分布 Fig.13Drag distribution with area rule |
对比图 12和13可以发现,未采取面积律修形之前,机翼后缘附近存在一个较大的阻力贡献区域;经过机身修形之后,在其余部分基本保持一致的情况下,该区域的面积大为缩小,同时强度也得到抑制,从而在宏观上获得了减阻效果。
进一步再绘制面积律减阻前后计算模型表面的压力和等压线分布分别如图 14和15所示。

|
| 图 14等直机身的计算数模压力及等压线分布 Fig.14Pressure distribution and isobar without area rule |

|
| 图 15收缩机身的计算数模压力及等压线分布 Fig.15Pressure distribution and isobar with area rule |
如图 14所示,未修形时,流经机翼表面的流场正常地在机翼前半部迎风区形成高压区,在机翼后半部背风区形成低压区,综合形成了较大的压差阻力。
修形之后,机身的收缩和恢复至原直径的变化分别使流场出现一道膨胀波和一道激波,并且都作用到了机翼表面,干扰了机翼的正常流场。机身收缩段在前,因此膨胀波的低压区作用在机翼迎风的前半部;机身恢复段在后,故而激波的高压区作用在了机翼背风的后半部。机身对机翼的干扰结果形成了附加的向前的力,在一定程度上抵消了机翼正常的压差阻力,从而实现了减阻。
由此,前文中得到的机身最大收缩位置应设计在机翼(及其他部件)所导致的横截面积增量最大的位置之后的结论也有了合理的解释,即:当激波产生的高压区能够最大面积地覆盖机翼最大厚度之后的背风区时,面积律减阻的效果最好。为了确保这一点的实现,自然需要机身最大收缩位置位于机翼导致的横截面积增量最大位置之后。
由此可见,通过CFD的详细分析,可以得出造成减阻效果的面积律流动机理,从而解释面积率减阻的根本原因;同时进一步可以据此得出能够指导飞机设计的相关设计准则,有利于跨声速设计空气动力学的精细化发展。
5 面积律近场流动机理的应用及验证 5.1 机身收缩剖面形状的设计根据第4节的分析,面积律减阻的本质是收缩机身产生的膨胀波和激波作用在机翼上所导致的有利干扰,因此收缩的目标为产生有利的膨胀波和激波,即收缩的截面形状对于飞行器而言是可设计的。这对于飞行器的总体布置而言,无疑在一定程度上可以缓解前文第2节中提到的最后一个问题。
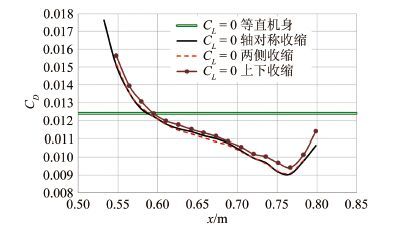
为了验证这一结论,按照前文机身最大收缩面积位置沿轴线变化的规律构造了一系列两侧收缩(保持机身高度不变)和上下收缩(保持机身宽度不变)的机身,再次计算了阻力随机身最大收缩面积所在位置之间的变化关系如图 16所示,同时也将轴对称收缩的结果绘制在一起,以便进行比较。
|
| 图 16 3种收缩机身导致的阻力随机身最大收缩面积所在位置的变化 Fig.16 Drag comparison for three kinds of fuselage with location of maximum contraction area |
由此可见,两侧收缩和上下收缩的机身修形方式对于减阻都是有效的,两侧收缩的效果与轴对称收缩效果相当,上下收缩效果略逊一筹。这一结论无疑对于飞行器总体设计和气动设计而言都是非常有用的。
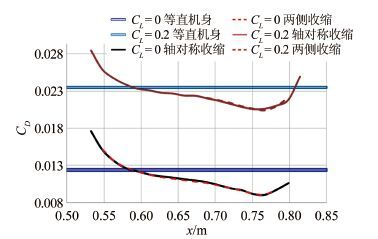
5.2 升力和迎角对于面积律减阻的影响前文的计算、分析和结论都是在迎角为0°(此时升力系数也为0)时得到的。为了验证飞行器正常飞行时以上各项结论是否仍然成立,本文选择了超声速飞行普遍需要的0.2的升力系数再次进行了计算,得出不同升力系数下阻力随机身最大收缩面积所在位置的变化规律如图 17所示,不同升力系数下阻力随机身最大收缩面积位置的变化规律如图 18所示。
|
| 图 17不同升力系数下阻力随机身最大收缩面积所在位置的变化 Fig.17 Drag comparison for varying lift with fuselage location of maximum contraction area |

|
| 图 18不同升力系数下阻力随机身最大收缩面积位置的变化 Fig.18 Variational drag for varying lift with various minimal fuselage diameter after contracion |
由图可见,不同的升力系数仅造成了面积律减阻之前的基本阻力的变化,而未影响前文研究得到的各种规律和现象。应用面积律的设计可以在0°迎角状态进行,所得到的减阻效果在各升力系数条件下均成立,因此可以使飞机跨声速减阻设计的工作量和复杂程度得到一定程度的缓解。
6 结 论经过本文的研究,基本明确了飞行器面积律减阻的近场流动机理,归纳起来可以得到以下结论:
(1) 经典跨声速面积律所确定的机身横截面积最大收缩量是减阻效果最优的,但其位置位于原始横截面积增量最大的位置之后的某处时,才能获得最好的减阻效果;
(2) 面积律的本质是相邻部件的有利干扰,通过适当的机身外形修形,实现机身激波后的高压区传递到机翼背风面,机身膨胀波后的低压区传递到机翼迎风面,形成前低后高的压力分布,产生向前的附加力,抵消了一部分正常阻力,从而达到减阻的效果;
(3) CFD方法可以成为风洞试验的补充,结合试验与CFD计算分析,可以有效地对试验中得到的一些现象进行定性和定量的分析,并得到合理的解释。
| [1] | Cole J D, Cook L P. Transonic aerodynamics[M]. Amsterdam: Elsevier Science Publishers , 2012 . |
| [2] | Chattot J, et al. Theoretical and applied aerodynamics[M]. New York: Springer Science+Business Media , 2015 . |
| [3] | Gu Y Q, Fan T X, Mou J G, et al. Drag reduction technology of jet-a review[J]. International Journal of Engineering Research in Africa , 2015, 17 (7) : 30–42. |
| [4] | Jameson A, Ou K. 50 years of transonic aircraft design[J]. Progress in Aerospace Sciences , 2011, 47 (5) : 308–318. DOI:10.1016/j.paerosci.2011.01.001 |
| [5] | David A. Computational sensitivity analysis for the aerodynamic design of supersonic and hypersonic air vehicles[R]. ADA622380, 2015. |
| [6] | Michael G. Computational analysis and characterization of RC-135 external aerodynamics[R]. ADA561659, 2012. |
| [7] | Forbes A, Patel A, Cone C, et al. Drag prediction for supersonic hydrogen-fueled airliners[R]. AIAA-2011-3968, 2011. |
| [8] | Palaniappan K, Jameson A. Bodies having minimum pressure drag in supersonic flow: Investigating nonlinear effects[J]. Journal of Aircraft , 2010, 47 (4) : 1451–1454. DOI:10.2514/1.C031000 |
| [9] | Dehpanah P, Nejat A. The aerodynamic design evaluation of a blended-wing-body configuration[J]. Aerospace Science and Technology , 2015, 43 (6) : 96–110. |
| [10] | Lyu Z, Joaquim R, Martins R. Aerodynamic design optimization studies of a blended-wing-body aircraft[J]. Journal of Aircraft , 2014, 51 (5) : 1604–1617. DOI:10.2514/1.C032491 |
| [11] | Roysdon P, Khalid M. Lateral-directional stability investigation of a blended-wing-body[R]. AIAA-2010-9617, 2010. |
| [12] | Utsumi Y, Obayashi S. Design of supersonic biplane aircraft concerning sonic boom minimization[R]. AIAA-2010-4962, 2010. |
| [13] | Ku Y C, Rho J H, et al. Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave[J]. Structural and Multidisciplinary Optimization , 2010, 42 (6) : 965–976. DOI:10.1007/s00158-010-0550-6 |
| [14] | Alyanak E. Modeling for conceptual design: an aeroelastic approach[R]. AIAA-2012-1425, 2012. |
| [15] | Christopher L O, Choi S. Design of optimum equivalent-area target for high-fidelity low-boom aircraft design[R]. AIAA-2015-2580, 2015. |
| [16] | Khalid A, Kumar P. Aerodynamic optimization of box wing-a case study[J]. International Journal of Aviation, Aeronautics, and Aerospace , 2014, 1 (4) : 1–46. |
| [17] | Berger C, Carmona K, et al. Supersonic bi-directional flying wing configuration with low sonic boom and high aerodynamic efficiency[R]. AIAA-2011-3663, 2011. |
| [18] | Zha G, Im H, Espinal D. Toward zero sonic-boom and high efficiency supersonic flight, part i: a novel concept of supersonic bi-directional flying wing[R]. AIAA-2010-1013, 2010. |
| [19] | Wintzer M, Kroo I. Optimization and adjoint-based CFD for the conceptual design of low sonic boom aircraft[R]. AIAA-2012-963, 2012. |
| [20] | Waddington M, McDonald R. Development of an interactive wave drag capability for the open VSP parametric geometry tool[R]. AIAA-2015-2548, 2015. |
| [21] | Guan X H. Supersonic wing-body two-level wave drag optimization using extended far-field composite-element methodology[J]. AIAA Journal , 2014, 52 (5) : 981–990. DOI:10.2514/1.J052305 |
| [22] | Feng X Q, Li Z K, et al. Research of low boom and low drag supersonic aircraft design[J]. Chinese Journal of Aeronautics , 2014, 27 (3) : 531–541. DOI:10.1016/j.cja.2014.04.004 |
| [23] | Berci M, Vigevano L. Sonic boom propagation with a non linear geometrical acoustic model[R]. AIAA-2011-2856, 2011. |
| [24] | Berci1 M, Igevano L. Sonic boom propagation revisited: a nonlinear geometrical acoustic model[J]. Aerospace Science and Technology , 2012, 23 (1) : 280–295. DOI:10.1016/j.ast.2011.08.003 |
| [25] | Haas A, Kroo I. A multi-shock inverse design method for low-boom supersonic aircraft[R]. AIAA-2010-843, 2010. |
| [26] | Jung T, Starkey R, et al. Design methods to create frozen sonic booms via lobe balancing using aircraft components[R]. AIAA-2011-2857, 2011. |
| [27] | Damljanovic D, Vitic A, et al. Testing of AGARD-B calibration model in the T-38 transonic wind tunnel[J]. Scientific Technical Review , 2006, 56 (2) : 52–62. |



