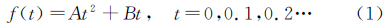由于研制高超声速飞行器和超燃冲压发动机带来的减阻需求,摩擦阻力的测量方法研究在近年来取得了一定的进展。对于高超声速飞行器和高超声速推进器而言,摩擦阻力的影响十分巨大,例如对乘波体外形高超声速飞行器,摩擦阻力占总阻力50%左右[1]。因此对于这类飞行器气动布局设计和超燃冲压发动机的设计来说,摩擦阻力是非常重要的性能指标。
测量高超声速摩擦阻力的方法主要有2种,第一种是CFD方法,第二种是实验方法。在摩擦阻力特性的研究中,地面实验结果可以与CFD计算相结合,为CFD计算提供实验依据和参照。设计人员可以根据摩擦阻力的预测结果对设计做出调整。
摩擦阻力的实验测量方法主要可分为直接测量和间接测量。直接测量的主要手段就是利用摩擦阻力天平,通过在模型表面齐平安装的浮动头来感受气流带来的摩擦阻力。国内外的研究机构主要应用了
应变型、压电陶瓷型与光纤型3类摩擦阻力天平进行摩擦阻力直接测量研究。美国弗吉尼亚理工大学[2, 3, 4, 5]、俄罗斯科学院西伯利亚分部(ITAM)、日本太空开发署和东京技术学院[6]等研究机构应用应变式天平进行了实验和研究。其中弗吉尼亚理工大学在高焓超燃冲压发动机摩擦阻力测量实验中不确定度可达11%~16%[7],IATM的平板摩擦阻力测量不确定度为10%~14%[8]。在国内中国航天空气动力技术研究院利用应变式天平进行的平板摩擦阻力测量实验中误差为7.6%~20%[9]。澳大利亚昆士兰大学研制了压电陶瓷式天平来测量摩擦阻力[10],在国内,中国空气动力研究与发展中心也利用压电陶瓷型天平进行了摩擦阻力测量,不确定度小于15%[11]。另外,印度科学院也研制了光纤型天平并进行相关研究[12]。
相对于其他测量方法和计算方法,摩擦阻力天平的优势在于直接测量,无需工程假设,可避免工程计算方法引起的系统误差;天平可内置于模型壁面之下,在流场之外,不干扰流场;易于标定和计量;易于进行热防护和温度修正;响应速度快,可用于脉冲风洞中进行毫秒级时间长度的测量;测量分辨率高;可以同时测量摩擦阻力的大小和方向;可用于曲面测量。同时摩擦阻力天平在技术方面也存在某些缺点:天平尺寸大,在设计模型过程中有更多的困难;天平和模型之间存在变形间隙,会给测量带来一定误差;测量表面较大,无法进行真正意义上的点测量。
在以往的研究中,中国航天空气动力技术研究院曾进行了带压缩拐角的平板摩擦阻力测量实验,用两分量应变天平测量了平板和压缩拐角斜面的摩擦阻力。还进行了可移动探针对流场施加扰动状态下的平板摩擦阻力测量,在这个实验中使用了单分量应变天平,实验数据重复性误差为7.6%~20%[9]。
基于之前实验的积累,中国航天空气动力技术研究院进一步完善了摩擦阻力测量的相关方法。采用应变型天平进行了2类摩擦阻力测量实验,一类是针对进气道和超燃冲压发动机内流场的,主要研究对象是平板模型压缩拐角和激波入射干扰工况下摩擦阻力的测量;另一类是针对飞行器外流场的,主要研究对象是乘波体布局模型腹部的摩擦阻力测量。下文针对这2类实验分别进行介绍。
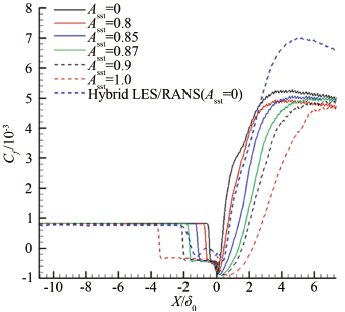
1 压缩拐角运动实验 1.1 摩擦阻力天平结构设计根据实验的需要,设计了两分量摩擦阻力天平。天平由敏感元件和壳体组成,如图 1所示。壳体为敏感元件提供保护和安装基准。壳体中可填充硅油等进行进一步防护。为了降低温度对应变计贴合位置产生的热应力,敏感元件采用了折线和迷宫式的结构设计,延长热传导路径。
 |
| 图 1 摩擦阻力天平 Fig 1 Skin friction balance |
为实现点测量并兼顾灵敏度,天平测量平面为Φ5mm的圆形。天平材料选用超硬铝合金。天平量程0.05N。
实验前对2支天平进行了静态校准。表 1是校准结果。
| Balance | Calibration matrix | Accuracy error | Precision error |
| 1 | Sf1=3.1626dU1 Sf2=2.6185dU2 | 0.15% 0.17% | 0.03% 0.02% |
| 2 | Sf1=2.2548dU1 Sf2=3.6792dU2 | 0.16% 0.13% | 0.01% 0.01% |
| 注:表中Sf单位为N,dU单位为mV/V。 | |||
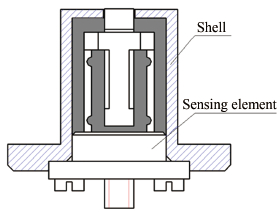
压缩拐角运动实验的目的是测量压缩拐角运动中摩擦阻力系数在流场中的分布状况。为了实现这个目的,设计制作了可用于压缩拐角流场的摩擦阻力测量实验装置。如图 2所示,装置由平板、摩擦阻力天平和可移动的压缩拐角机构组成。其中,可压缩拐角运动机构由伺服电机驱动,其斜面坡度为10°。平板上预留了2处天平安装位置,分别位于可运动压缩拐角远端与近端,二者中心相距60mm。摩擦阻力天平具有x、y 2个分量,天平安装时,2分量与来流方向夹角均为45°。因此在对称流场中天平2个分量测得的结果理论上应相等,且两分量载荷的合成为模型受到的轴向载荷。
 |
| 图 2 多用途摩擦阻力测量装置 Fig 2 Multi-purpose friction measuring device |
以平板流动摩擦阻力测量装置为基础,在平板上增加压缩拐角,其斜面作为扰动源,实验中斜面沿逆来流方向运动,使摩擦阻力天平和扰动流场产生沿气流方向的相对位移,实时同步采集摩擦阻力天平信号和机构位置信号,并计算每一个位置对应的摩擦阻力系数,可获得斜面前流场的摩擦阻力系数分布。压缩拐角极限运动位置为距离天平测量面1mm处。
由于压缩拐角由伺服电机驱动,且伺服电机与数据采集设备共用电源,为了减小伺服电机电源对数据采集设备带来电磁干扰(EMI),在伺服电机电源处加装了滤波器。
1.3 风洞与流场参数FD-03风洞为暂冲式高超声速风洞,具有自由射流试验段,上游有空气加热器,下游有二级引射器,实验p0=1MPa,T0=360K,M∞=5。喷管为二元喷管,喷管出口尺寸为170mm×170mm。
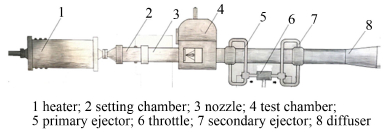 |
| 图 3 FD-03风洞简图 Fig 3 The sketch of wind tunnel FD-03 |
在实验中,流场稳定一定时间后,电脑向电机下达运动指令,压缩拐角扰动机构在电机的驱动下向前运动,运动至距离2号摩擦阻力天平测量面1mm处停留5s,之后返回原位置。实验过程中每秒采集10次数据。如图 5所示,得到天平的输出信号反映了压缩拐角的运动,2号天平的输出当压缩拐角停留在其边缘位置时出现了明显的下降。
 |
| 图 4 压缩拐角扰动机构逐步前移 Fig 4 Compression ramp gradually moves forward |
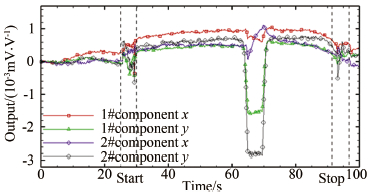 |
| 图 5 压缩拐角机构运动状态下的天平输出信号 Fig 5 The output of balance with compression ramp moving |
校准与实验采用同一套放大器和导线,不存在因测试系统变化带来的误差,测量传递比较准确。数据采集系统本身分辨率到小数点后第6位即10-6mV/V,小数点后第 5位即10-5mV/V数据的采集精度良好,满足实验要求。
在实验中,温度是对测量结果产生影响的主要误差项。温度的累积效应使测量结果曲线发生漂移,实验时间越长由温度造成的漂移量越大。
数据处理的基本步骤可以用图 6简单概括。
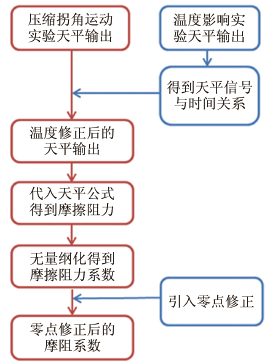 |
| 图 6 压缩拐角运动实验数据处理流程图 Fig 6 The flow chart of data processing of moving compression ramp experiment |
为了测试温度对天平信号的影响,在压缩拐角运动实验前,进行了多次压缩拐角不运动状态下的实验。如图 7所示,单次实验中各天平分量的输出信号均呈现出与时间的相关性,即温度的积累效应使输出曲线发生弯曲。
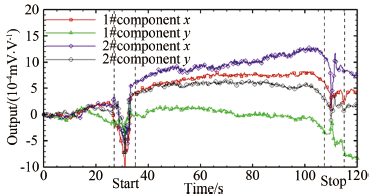 |
| 图 7 压缩拐角机构未运动状态下的天平输出信号 Fig 7 The output of balance without ramp moving |
选取了多次测试中的流场稳定后天平各分量信号与时间的关系曲线进行二次多项式拟合,在多次测试中二次多项式的二次项和一次项系数呈现良好的重复性。多项式形式如下:
以2号天平为例,图 8是2号天平2个分量在2次测试中流场稳定阶段的输出。
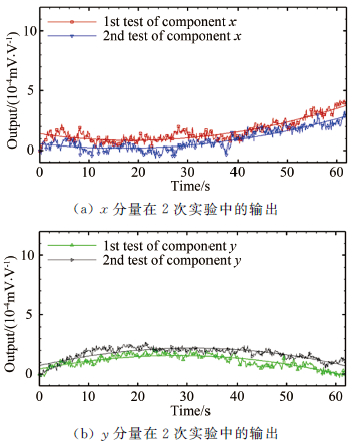 |
| 图 8 2号天平在2次测试中流场稳定阶段的输出 Fig 8 The output of balance 2# in the stable phase of 2 tests |
表 2给出了2号天平在这2次测试中拟合输出曲线的二次多项式的二次项和一次项系数。
| Component | Ordinal of tests | Quadratic term coefficient A | Monomial term coefficient B |
| Component x | 1st text 2nd test | 1.563×10-9 1.298×10-9 | -5.879×10-7 -4.349×10-7 |
| Average value | 1.431×10-9 | -5.114×10-7 | |
| Component y | 1st text 2nd test | -1.455×10-9 -1.549×10-9 | 8.128×10-7 9.597×10-7 |
| Average value | -1.502×10-9 | 8.863×10-7 |
结合图表可知,在这2次实验中天平输出曲线与时间具有一定的相关性,且二次多项式系数具有一定的重复性。因此推论压缩拐角运动实验中得到的输出与时间同样具有这样的相关性。用这2次实验中得到的二次项和一次项系数的均值作为新的拟合多项式系数,在输出曲线上减掉这个多项式即可得到去掉温度累积效应的天平输出曲线。具体的方法是在开车之后的输出信号上逐点减掉补偿量,即为温度修正后的天平输出信号。
将修正后的天平输出代入天平公式即可得到天平受到的两分量载荷。
由风洞的流场参数可以计算得到动压值,即可将载荷值无量纲化得到摩擦阻力系数。
将各分量摩擦阻力系数合成即得到流场轴线上的摩擦阻力系数,结果如图 12所示。
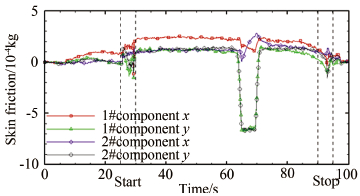 |
| 图 10 天平测得的摩擦阻力 Fig 10 Skin friction |
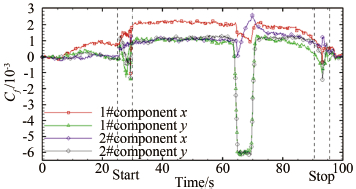 |
| 图 11 各分量摩擦阻力系数 Fig 11 Coefficient of skin friction |
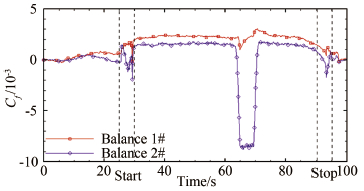 |
| 图 12 合成后的摩擦阻力系数 Fig 12 The coefficient of resultant of skin friction |
在图 9中可以看到,距离压缩拐角更近的2号天平测得的摩擦阻力系数在压缩拐角运动至天平边缘处时突变为负值,在压缩拐角迫近过程中摩阻系数没有明显波动,这个实验现象表明压缩拐角对流场的影响范围很小。而1号天平距离2号天平有60mm,因此当压缩拐角在2号天平边缘处时无法对1号天平周围流场产生明显的干扰。因此可以明确1号天平测得的摩擦阻力系数在压缩拐角运动中出现波动并非由于流场波动导致。这个实验现象真实原因尚不明确。
 |
| 图 9 温度修正后的天平输出信号 Fig 9 The output with temperature correction |
在统计了多次实验,汇总天平各分量测得的摩擦阻力系数后,针对不同的流动类型由表 3给出了实验测量的均值和不确定度。
| Type of flow | Cf of each component | Uncertainty |
| Plate flow | 0.00124 | 11.01% |
| Ramp interfere | -0.00566 | 4.57% |
文献[13]利用大涡模拟与雷诺数平均模型杂合方法(LES/RANS)和雷诺数平均N-S模型(RANS)模拟 了二维压缩拐角流动中平板的摩擦阻力系数。文献[13]选取的模型为28°压缩拐角,p0=2.17MPa,T0=350K,M∞=4.95。
图 13中X/δ0表示与压缩拐角边缘的距离,X/δ0<0为远离压缩拐角的一侧。图 13显示在靠近压缩拐角边缘处,即激波边界层干涉区域内,摩擦阻力系数出现负值。实验中摩擦阻力的变化现象与此吻合。
2 乘波体实验 2.1 实验设备与天平介绍乘波体实验的目的主要是测量在高超声速飞行状态下乘波体底面的摩擦阻力,并测量不同迎角状态下的摩擦阻力变化趋势。
乘波体模型通过一个插入式迎角机构固定在风洞内。摩擦阻力天平安装在乘波体模型底部的凹槽内,2个天平沿模型轴线分布,如图 14所示。
 |
| 图 14 乘波体模型与天平安装位置 Fig 14 The model of wave rider and the installation of balance |
在乘波体实验中,采用了与压缩拐角实验中相同的天平设计,但修改为单分量。天平量程0.05N。
实验前对天平进行了静态校准。表 4是校准结果。
| Balance | Calibration matrix | Accuracy error | Precision error |
| 1 | Sf=-0.142dU2+3.75dU | 0.16% | 0.02% |
| 2 | Sf=0.1874dU2+2.974dU | 0.19% | 0.01% |
| 注:表中Sf单位为N,dU单位为mV/V。 | |||
乘波体实验在FD-07风洞进行,FD-07风洞是一座自由射流暂冲式高超声速风洞。喷管出口直径为Φ0.5m。试验马赫数为5~12。实验中p0=1MPa,T0=360K,M∞=5。
2.3 实验过程在实验过程中,流场建立前模型保持在流场之外,流场稳定后插入式迎角机构带动模型进入流场,随后模型的迎角由0°逐渐变化至5°,由5°至10°,最终由10°回归0°。每次变化时间约1.3s,在0°、5°和10°状态分别保持约5s。每秒共采集10次数据。
2.4 数据处理与误差分析在本实验中,对测量结果可能产生影响的主要干扰项有天平自重和温度这2项。其中天平自重项是指在模型的运动过程中,天平重力方向与天平轴向发生变化,使得天平的输出发生改变。温度项是指在吹风过程中,温度逐渐上升产生的累积效应使得天平输出发生变化。因此在数据处理中需要针对这2项误差进行修正。
数据处理的基本步骤可以用图 15中的流程图简单概括。
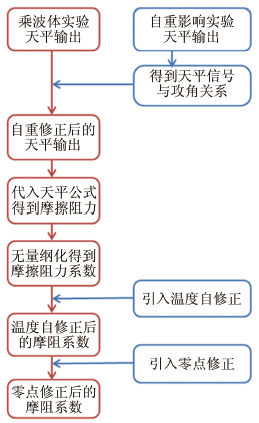 |
| 图 15 乘波体实验数据处理流程图 Fig 15 The flow chart of data processing of wave rider experiment |
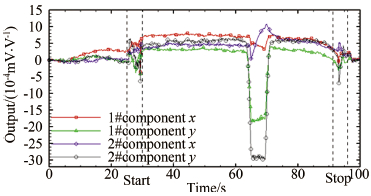
针对自重引起的误差,在未吹风状态先取得天平在改变迎角运动中的信号输出。如图 16所示。由此可以得到单位角度的改变量会对天平读数带来的增量。在每车次吹风前,都进行这个测量。
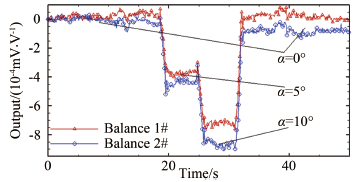 |
| 图 16 模型迎角运动导致天平输出变化 Fig 16 The output brought by the change of attack angle |
取得天平在吹风状态下的输出信号,如图 17所示。根据实验中模型的运动过程据点加入相应的自重修正量,之后可以得到图 18中的结果。
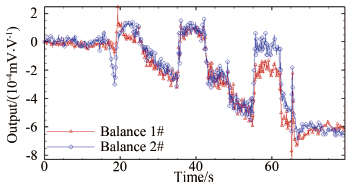 |
| 图 17 风洞实验中的天平输出 Fig 17 The output in the wind tunnel test |
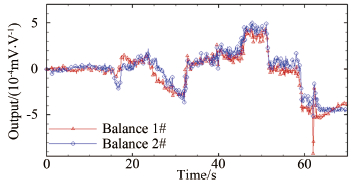 |
| 图 18 引入自重修正的天平输出 Fig 18 The output with weight correction |
将天平输出代入天平公式,即可得到天平测得的载荷值。由风洞的流场参数可以计算得到动压值,即可将载荷值无量纲化得到摩擦阻力系数,如图 19所示。
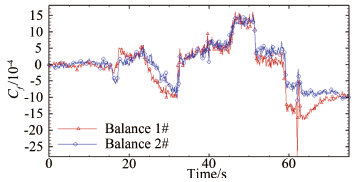 |
| 图 19 摩擦阻力系数 Fig 19 Coefficient of skin friction |
从图 19中可以看到,曲线呈现一定的下降趋势,需要引入温度修正来抵消温度累积效应引起的误差。在本实验中没有采用压缩拐角实验中的温度修正方法,原因是在不同迎角下热流密度存在差异,不能通过单一的二次多项式进行拟合。在本实验中,将每条输出曲线的一阶渐近线作为温度影响的拟合。在获得实验中天平输出的线性拟合后,依照拟合得到的直线斜率逐点增加递增的补偿量。
如图 20所示,经过温度修正后基本排除了温度效应的影响,可以观察到上图的摩擦阻力系数曲线初零点和末零点之间仍存在一个偏移量。这个偏移量的主要产生原因是风洞起动和关机引起的冲击带来的信号不回零。参考常规的数据处理方法,取初、末零点的平均值,用该值对整条曲线进行平移。得到修正后的结果如图 21所示。
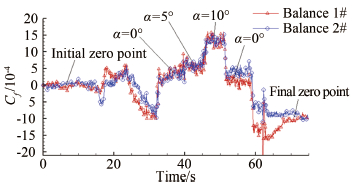 |
| 图 20 温度修正后的摩擦阻力系数 Fig 20 The coefficient with temperature correction |
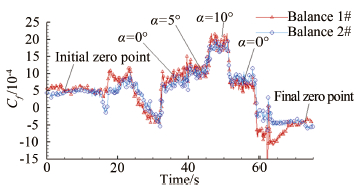 |
| 图 21 引入零点修正后的摩擦阻力系数 Fig 21 The coefficient of skin friction with zero correction |
通过上述实验结果可以得出模型下表面中心上的摩擦阻力与模型迎角之间的关系,如图 22所示。从图 22中可以看到,摩擦阻力系数与迎角呈正相关。
 |
| 图 22 摩擦阻力系数与迎角的关系 Fig 22 Relationship between coefficient of skin friction and angle of attack |
2个天平在多次试验中测得0°迎角下摩擦阻力系数均值为0.0007,5°迎角下为0.0010,10°迎角下为0.001 75。1号天平测量不确定度为4.8%,2号天平测量不确定度为7.9%。
3 结 论在上述2个实验中,使用应变型天平在高超声速风洞中进行了模型表面摩擦阻力系数测量,得到以下结论:
(1) 高超声速摩擦阻力测量实验表明,无论是内外流场,摩擦阻力的量值都比较小,对摩阻天平要求较高,为获得可靠的数据有必要针对天平进行筛选,测试实验也应当增加重复车次以提高实验数据的置信度;
(2) 在压缩拐角运动实验中,压缩拐角的运动导致激波位置移动,摩擦阻力系数的变化反映了激波干扰带来的影响。实验现象与文献[13]计算模拟的摩擦阻力变化规律吻合较好,但由于工况不同等原因有量值差别。摩擦阻力测量装置前端安装的天平输出在压缩拐角运动时出现波动,这种波动不是由流场扰动引起的,真实原因需要进一步研究;
(3) 在乘波体实验中,模型下表面中心线上的摩擦阻力系数随迎角的增大而增大;
(4) 2组实验中,最佳实验不确定度优于5%,整体实验不确定度优于12%,技术水平和国外文献相当。
| [1] | Silverster T B, Morgan R G. Skin-friction measurements and flow establishment within a long duct at superorbital speeds[J]. AIAA Journal, 2008, 46(2):527-536. |
| [2] | Smith T B, Schetz J A, Bui T T. Development and ground testing of direct measuring skin friction gages for high enthalpy supersonic flight tests[D]. Blacksburg:Virginia Polytechnic Institute and State University, 2001. |
| [3] | Schetz J A. Direct measurement of skin friction in complex flows[C]//Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, USA. 2010:1-28. |
| [4] | Bowersox R, Schetz J, Chadwick K, et al. Direct measurements of skin friction in hypersonic high enthalpy impulsive scramjet experiments[R]. AIAA-94-0585, 1994. |
| [5] | Magill S, MacLean M, Schetz J, et al. Study of direct-measuring skin-friction gauge with rubber sheet for damping[J]. AIAA Journal, 2002, 40(1):50-57. |
| [6] | Tsuru T, Tomioka S, Kudo K, et al. Skin-friction measurements in supersonic combustion flows of a scramjet combustor[R]. AIAA-2008-4578, 2008. |
| [7] | Chadwick K, Schetz J. Direct measurements of skin friction in high-enthalpy high-speed flows[R]. AIAA-92-5036, 1992. |
| [8] | Goldfeld M, Nestoulia R, Falempin F. The direct measurement of friction in the boundary layer at supersonic flow velocities[R]. AIAA-2001-1769, 2001. |
| [9] | 马洪强, 高贺, 毕志献. 高超声速飞行器相关的摩擦阻力直接测量技术[J]. 实验流体力学, 2011, 25(4):83-88. Ma H Q, Gao H, Bi Z X. Direct measurement of skin friction for hypersonic flight vehicle[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4):83-88. |
| [10] | Goyne C P, Stalker R J, Paull A. Transducer for direct mea-surement of skin friction in hypervelocity impulse facilities[J]. AIAA Journal, 2002, 40(1):42-49. |
| [11] | 吕治国, 李国君, 赵荣娟, 等. 激波风洞高超声速摩擦阻力直接测量技术研究[J]. 实验流体力学, 2013, 27(6):81-85. Lyu Z G, Li G J, Zhao R J, et al. Direct measurement of skin friction at hypersonic shock tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6):81-85. |
| [12] | Bland S M, Sang A K, Schetz J, et al. Improved direct measurement fiber-optic skin friction gauge for flight test and laboratory applications[C]// 25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference.2006:3836. |
| [13] | Edwards J R. Simulation of transient dynamics of shock wave boundary layer interactions using hybrid large-eddy/Reynolds-averaged Navier-Stokes models[R]. North Carolina State University at Raleigh, 2007. |