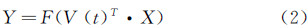飞机穿越含有过冷水滴(温度低于冰点但仍保持液态的水滴)时会遭遇结冰现象[1, 2],结冰会改变表面的流场分布、破坏飞机的气动性能、导致部件载荷分布发生变化,使操纵性和稳定性受到影响,轻则使飞机的安全飞行范围减小,重则导致机毁人亡的严重事故[3, 4]。
结冰风洞试验是当前研究飞机结冰的主要方式之一。航空工业发达的国家对飞机结冰问题相当重视,建造了大量研究型和生产型结冰风洞,代表性的结冰风洞有美国NASA格林研究中心的IRT结冰风洞、意大利CIRA的IWT结冰风洞[5, 6, 7, 8]以及中国空气动力研究与发展中心的多功能结冰风洞等。
结冰风洞的试验参数除了常规的空气来流条件外,还包括水滴容积平均直径(MVD)和液态水含量(LWC) 2个重要的结冰云雾参数。实验过程中,现有的结冰风洞试验技术很难稳定控制云雾参数,不同温度或者时间条件下,结冰云雾参数会出现波动或变化;另外,受测量设备及技术限制,现阶段测量结冰云雾参数时往往存在较大误差。云雾参数的控制能力和试验过程中相关参数的精确测量这2方面的技术瓶颈导致结冰试验中所输入的试验云雾条件本身就可能存在较大误差,意大利CIRA 的结冰风洞IWT所标定的液态水含量误差就达到了20%[9]。结冰云雾参数的误差将会导致试验结果与需要模拟的真实情况存在明显的差别,研究结冰过程中云雾参数误差传递的规律及影响,建立合理的结冰试验误差分析和试验结果修正方法,对于消除由于试验云雾参数输入条件误差所带来的影响以及相关的飞机结冰研究有重要的理论和工程意义。
结冰风洞试验需要得到物体表面的结冰外形,试验结果的修正主要是针对冰形的修正。国内由于建设结冰风洞的时间不长,结冰风洞试验数据的修正理论和方法研究目前尚属空白。国外仅仅探索了冰形的特征化描述方法[10],暂时没有开展冰形修正方面的研究。
本文结合飞机结冰的数值分析方法,以NACA0012翼型为研究对象,分析结冰过程中云雾参数导致冰形误差的传递规律及影响,采用人工神经网络方法,开展考虑液态水含量和水滴粒径这2个云雾参数的冰形修正方法的探索性研究。
1 冰形修正基本理论冰形修正方法的建立过程实质上是一个优化设计的过程,首先必须有一个基本的目标函数,取为修正后的冰形与目标冰形的相对误差,进一步建立冰形修正模型以及相应的修正方法,使得修正后的冰形与目标冰形吻合得更好。但是,由于冰形表现形式多样,冰形数据通常以离散点的方式储存,很难对2个冰形进行量化对比,现阶段还没有一个具有普适性的冰形相对误差的量化计算方法。因此,冰形修正方法的首要问题是建立冰形相对误差的定量计算方法。
与普通的图形识别方法不同,2组冰形之间的量化误差不仅仅需要考虑图形本身之间的差异,更重要的是还需衡量由于形状差异导致的气动性能的差异,因此,用于微观方面差异识别的基于矢量、三角剖分等算法的匹配方法并不适用于冰形误差的量化评估。本文采用平均冰形几何特征量对比的方法对2组冰形的相对误差进行量化计算。
飞机结冰是由于过冷水滴撞击到机体表面而发生相变的现象,空气含水量、过冷水滴温度以及冻结过程中释放潜热排走的速度等方面的差异将会导致冻结过程形成的冰层在结构、强度和外观上有显著的区别。冰形相对误差的量化方法与冰形宏观几何轮廓密切相关,冰的外形轮廓大体上可以分为流线型和角状型2大基本类型[11],如图 1所示。
 |
| 图 1 典型冰形 Fig 1 Typical ice shape |
结冰会改变飞机表面的外形,进而影响飞机的气动特性和飞行特性,冰形误差的量化评估方法必须建立在结冰对飞机性能影响的基础上,扰动源的宏观轮廓是对空气流场影响度的主要决定因素,冰的宏观轮廓可以通过提炼冰形几何特征量的方法来描述,针对流线型和角状型2种不同的冰,可分别提炼出不同的几何特征量。
美国NASA格林研究中心的Ruff等人提出了一种角状冰的特征量方法,采用8个特征量来描述典型的角状冰,分析发现,这种方法存在一些可以改进之处,例如,其中最大厚度和宽度这2个特征量可以通过冰角长度及角度来体现。
冰形特征量的建立,主要是为了从冰的宏观轮廓方面来衡量结冰外形对气动特性的影响,从空气动力学的角度来分析,角状冰最关键的参数是2个冰角及对应的长度、驻点处结冰厚度和冰位置的偏转角。因此,冰形特征量可以由以下8个特征量来描述:驻点厚度Ts,驻点偏转角At,冰角特征包括上、下冰角的长度(Hu和Hl)以及上下冰角的角度(Au和Al),结冰极限特征包括上极限Su和下极限Sl。
流线型冰相对比较简单,采用驻点厚度Ts,驻点偏转角At,冰宽度特征包括最大宽度Wm,结冰极限特征包括上极限Su和下极限Sl等5个特征量就能基本描述其宏观轮廓,2种典型冰形修正方法的建立过程完全类似,本文以复杂的角状冰为例,对冰形的修正方法进行探索。
不可能直接针对描述冰形的所有离散点进行修正,从特征量的提炼过程可知几何特征量可以衡量冰形导致气动性能的差异,因此,冰形修正时,可以先针对冰形的基本几何特征量进行修正,根据修正后的特征量得到相关特征点的修正坐标,进而采用TFI方法[12]得到修正后的整个冰形。
 |
| 图 2 冰形特征量 Fig 2 Geometric characteristics of ice |
云雾参数只有在较小的误差范围才能采用修正方法对实验结果进行处理,误差超过一定范围后,则必须从试验方法和设备等角度进行改进。通常云雾参数的较小输入误差不会使冰形发生根本性变化,修正前后的冰形不会改变其基本特征。冰形修正过程中,分析云雾参数与各特征量的传递规律及敏感性,建立特征量修正模型,进一步根据特征量的修正量对冰形进行修正。
冰形及其特征量受基体几何尺寸、液态水含量、水滴粒径、来流速度、温度和结冰时间等多个参数的共同影响,需要通过对各参数的影响程度进行准确分析,才能建立合理可靠的修正模型。参数灵敏度分析的目的是计算各参数对冰形特征量的影响因子,所得影响因子用于后续参数修正模型的建立。现有技术条件下,结冰风洞中可以较为精准地控制来流速度、温度和结冰时间这3个量,而现有的结冰风洞试验技术很难稳定控制云雾参数,液态水含量和水滴粒径往往可能存在一定误差。由于同时考虑所有因素及其耦合作用对的冰形修正方法过于复杂,为降低难度,针对各影响因素采用分步修正的方法,由于现阶段误差最大的因素为液态水含量和水滴粒径这2个输入量,本文仅考虑基于这2个云雾参数误差进行冰形修正的情况,后续将开展综合其他因素进行冰形修正的研究。
在结冰这一复杂过程中,冰形特征量与控制参数之间关系的系统方程过于复杂,各参数的灵敏度指标(一般取为一阶灵敏度系数,即系统输出对系统参数的一阶导数)无法直接计算得到,而人工神经网络技术在复杂非线性关系的近似模拟方面具有独到的优势,本文借鉴人工神经网络技术[13, 14, 15]建立了冰形特征量的修正方法。
图 3为冰形与云雾参数之间的复杂非线性关系系 统的神经网络拓扑结构图,其中:输入向量:X =(x0,x1,x2,…,xn)T;隐层输出向量:Y =(y0,y1,y2,…,ym)T;输出层输出向量:O =(o1,o2,…,ol)T;期望输出向量: d =(d1,d2,…,dl)T。
 |
| 图 3 三层BP模型 Fig 3 Three-layer BP model |
x0,x1,x2……xn分别代表液态水含量、水滴粒径等输入参数;o0,o1……ol分别代表采用人工神经网络方法预测的冰形特征量;d1,d2,…,dl分别代表冰形期望特征量,也即是数值预测或冰风洞试验得到的冰形特征量。
V =(V1,V2,…,Vm)、 W =(W1,W2,…,Wl)分别为输入层到隐层、隐层到输出层之间的权值矩阵。
人工神经元有一个变换函数,用于执行对该神经元所获得网络输入量的转换,这就是激活函数,它可以将神经元的输出进行放大处理或限制在一个适当的范围内,隐层和输出层的激活函数可取为:
例如,隐层和输入层之间的关系可通过如下公式来描述:
冰形特征量的修正值计算公式如下:
i=1,2……8分别代表8个不同的特征量,Ctim为第i个特征量修正值,Cti为实验值,fn为采用人工神经网络方法得到的冰形特征量,fn(X+ΔX)-fn(X)为冰形系统模型在X附近的敏感度指标。冰形系统模型过于复杂,当存在多个输入变量需要修正时,采用分步修正的方法,每一步中对特定系统参数进行微小摄动,固定其它参数值进行修正,有多少个需要修正的量则就分多少步进行修正。
3 冰形修正方法为使得冰形修正方法具有较好的普适性,冰形特征量尽量选用无量纲量,同一个物理量可以采用多种无量纲化处理方法,以冰角长度及上下极限等长度量为例,可分别用冰形特征尺寸和翼型几何尺寸这2个基本长度量进行无量纲化,从结冰的基本原理可知,冰角长度主要与过冷水收集率密切相关,与翼型几何尺寸关系不大,而上下极限则主要与翼型几何尺寸密切相关,与过冷水收集率关系不大。因此,针对上、下冰角长度及驻点厚度,基于冰形特征尺寸进行无量纲化,如采用Hu=Hu/L∞,其中L∞为对应状态下的冰形特征尺寸,定义为收集率为1时对应状态下的结冰厚度L∞=LWC·v·t/ρi,式中的液态水含量、来流速度和结冰时间这3个量为对应状态中的实验值;针对上、下极限,采用翼型几何尺寸进行无量纲化,如Su=Su/L,其中L为翼型几何尺寸。
基于特征量修正模型得到修正后的冰形几何特征量后,可得到修正后的上下极限点、上下冰角点以及驻点这5个特征点的坐标。上冰角及上冰角对应的冰厚度,采用二分法即可得到对应的上冰角特征点坐标,同样可以得到下冰角特征点及驻点处的坐标。
冰形小范围误差范围内的修正处理不会发生冰形特征的颠覆性变化,根据上部分的方法得到特征量的修正值后,可以在试验冰形的基础上进一步修正得到新的冰形。修正后的冰形数据点坐标[16]为:
i是冰形数据点序号,dxc1、dxc2和dyc1、dyc2是冰形数据点两侧的特征点在X和Y方向的修正量,Φ是沿着冰形曲线的型函数,分别为:
图 4为根据基础冰形以及特征点的坐标变化值,采用上述修正方法处理得到冰形的典型情况。
 |
| 图 4 冰形修正示意图 Fig 4 Ice modification |
本文仅考虑针对液态水含量和水滴粒径这2个云雾参数进行冰形修正,以NACA0012翼型为例,分别对MVD和LWC这2个参数进行摄动,同时固定其它参数取值,其中基础冰形和目标冰形均采用数值仿真方法得到,进行了2组情况的算例验证。
(1) Case1
本算例中,T=-9℃,v=62m/s,t=2000s,L=0.5334m,α=0°,这几个变量维持不变,MVD在15~50μm范围内、LWC在0.3~2.0g/m3范围内波动,取16组样本输入条件,采用数值仿真方法得到对应的16组目标冰形。采用人工神经网络方法,基于这16组样本数据,建立冰形特征量与云雾参数的非线性对应关系。
若实验需要模拟MVD=20μm,LWC=0.55g/m3条件下的冰形,实施过程中由于控制、测量或实验条件受限等原因使得真实实验条件为MVD=25μm,LWC=0.65g/m3,采用本文的修正方法对冰形进行修正,图 5为修正前后冰形与目标冰形的对比情况,目标冰形采用数值方法模拟目标实验条件得到。
 |
| 图 5 修正前后的冰形 Fig 5 Ice with and without modification |
与上个状态相反,若实验需要模拟MVD=25μm,LWC=0.65g/m3条件下的冰形,实施过程中由于控制、测量或实验条件受限等原因使得真实实验条件为MVD=26μm,LWC=0.55g/m3,图 6为修正前后冰形与目标冰形的对比情况。
 |
| 图 6 修正前后的冰形 Fig 6 Ice with and without modification |
从图 5和6中可看出,尽管在下冰角位置,修正后的冰形与目标冰形还存在一定误差,但总体来说,修正以后的冰形与目标冰形的吻合程度明显高于修正前,尤其是在上冰角、驻点和上下极限附近,修正以后的冰形与目标冰形吻合度较好,说明该修正方法适用于本组算例条件,修正后的数据能够起到提高试验精度的目的。
(2) Case2
本算例中,T=-5℃,v=62m/s,t=2000s,L=0.5334m,α=0°,这几个变量维持不变,MVD在15~50μm范围内、LWC在0.25~2.0g/m3范围内波动,取16组样本输入条件并采用数值方法得到对应的目标冰形。
与上个算例类似,基于MVD=30μm,LWC=0.45g/m3的冰形,采用修正方法得到MVD=35μm,LWC=0.55g/m3条件下的冰形如图 7所示;基于MVD=35μm,LWC=0.55g/m3的冰形,采用修正方法得到MVD=30μm,LWC=0.45g/m3条件下的冰形如图 8所示。
 |
| 图 7 修正前后的冰形 Fig 7 Ice with and without modification |
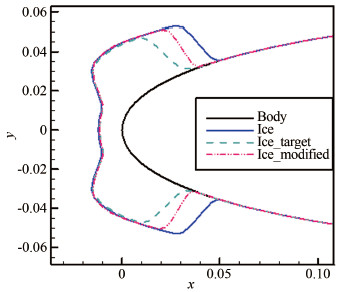 |
| 图 8 修正前后的冰形 Fig 8 Ice with and without modification |
从图 7和8中可看出,在本组算例条件下,修正以后的冰形与目标冰形的吻合程度也有明显的改善。本组算例修正结果与目标结果误差要稍大于Case1中的值,主要原因在于本文的修正方法主要基于冰形典型几何特征量以及无限插值方法,对于相邻特征点之间的冰形曲线过渡较为平缓的冰具有较好的修正效果。例如,对于典型的角状冰,如Case1中的冰形,各特征点之间没有较大拐点,修正冰形与目标冰形吻合良好。而Case2中的冰形,上冰角点与上极限点、下冰角点与下极限点之间的冰形曲线中分别存在一个较大的拐点,修正冰形与目标冰形在拐点附近的吻合度较差,应用该方法对这种类型的冰形进行修正时,能有一定效果,但误差会稍大于相邻特征点之间没有大拐点的冰形。
5 结论本文结合人工神经网络方法,提出了一种基于云雾参数误差的结冰外形修正方法,采用CFD手段对所提出的方法进行了验证,得到如下结论:
(1) 采用数据点方法的冰形存储方式难以进行修正前后的量化对比,基于几何特征量的冰形函数可以为冰形修正提供量化的目标函数;
(2) 实验条件与冰形的关系极其复杂,即使仅仅考虑液态水含量和水滴粒径这2个变量,采用人工神经网络方法所得到的这种关系也存在较大误差,但所建立的非线性关系基本能体现冰形沿着云雾参数变化发展的大体趋势。本文方法中的修正量为2个预测值的差,即使所建立的实验条件与冰形对应函数本身具有一定误差,只要该函数的趋势正确,修正方法就存在合理性,本文2个算例也验证了这一结论,当云雾参数在小范围内波动时,本文的修正方法具备一定的工程实用性;
(3) 冰风洞试验过程中,冰形生成不仅仅与云雾参数相关,还与飞行姿态、飞行状态等参数密切相关,是一个极其复杂的现象。在误差较小时,应用本文方法能起到明显提高试验精度的目的,但修正冰形仍然与目标冰形存在一定的差异。
本文工作仅仅是对冰形修正方法进行了初步的探索,后续将力争综合飞行姿态以及飞行状态等相关参数,建立适用范围更宽、精度更高的冰形修正方法。
| [1] | 杨倩, 常士楠, 袁修干. 水滴撞击特性的数值计算方法研究[J]. 航空学报, 2002, 23(2):173-176. Yang Q, Chang S N, Yuan X G. Study on numerical method for determ ining the droplet trajectories[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(2):173-176. |
| [2] | 易贤, 王开春, 桂业伟. 结冰面水滴收集率欧拉计算方法研究及应用[J]. 空气动力学学报, 2010, 28(5):596-608. Yi X, Wang K C, Gui Y W. Study on Eulerian method for icing collection efficiency computation and its application[J]. Acta Aerodynamica Sinica, 2010, 28(5):596-608. |
| [3] | Yves Bourgault, Wagdi G Habashi, Julien Dompierre. A finite element method study of eulerian droplets impingement models[J]. Internernational Journal for Numerical Methods in Fluids, 1999, 29:429-449. |
| [4] | Bragg M B, Broeren A P, Addy H E, et al. Airfoil ice-accretion aerodynamics simulation[R]. AIAA-2007-0085, 2007. |
| [5] | Bragg M B, Broeren A P, Blumenthal L A. Iced-airfoil aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41(5):323-418. |
| [6] | Lee S, Bragg M B. Effect of simulated-spanwise ice shapes on airfoils:experimental investigation[R]. AIAA-99-0092,1999. |
| [7] | Anderson D N. Further evaluation of traditional icing scaling methods[R]. AIAA-96-0633, 1996. |
| [8] | Michael Papadakis, Hsiung-Wei Yeong, Koji Shimoi, et al. Ice shedding experiments with simulated ice shapes[R]. AIAA-2009-3972. |
| [9] | Italian Aerospace Research Centre. CIRA icing wind tunnel user manual[R]. CIRA, 2007. |
| [10] | Ruff G A. Quantitative comparison of ice accretion shapes on airfoils[J]. Journal of Aircraft, 2002, 39(3):418-426. |
| [11] | Bragg M B, Gregorek G M. Aerodynamic characteristics of airfoils with ice accretions[C]. AIAA 20th Aerospace Sciences Meeting, 1992, Orlando, Florida. |
| [12] | 周志宏, 李凤蔚, 李广宁. 基于两相流欧拉方法的翼型结冰数值模拟[J]. 西北工业大学学报, 2010, 28(1):138-142. Zhou Z H, Li F W, Li G N. Applying eulerian droplet impingement model to numerically simulating ice accretion but with some improvements[J]. Journal of Northwestern Polytechnical University, 2010, 28(1):138-142. |
| [13] | Li H J. Neural network modeling and optimization of semi-solid extrusion for aluminum matrix composites[J]. Journal of Materials Processing Technology, 2004, 151(3):126-132. |
| [14] | Sterjovski Z, No lan D. Artificial neural networks for modelling the mechanical properties of steels in various applications[J]. Journal of Materials Processing Technology, 2005, 170:536-544. |
| [15] | Saltelli A. Sensitivity analysis[M]. Chichester:Wiley, 2000. |
| [16] | Yuan C L, Jeng Y N. A transfinite interpolation method of grid generation based on multipoints[J]. Journal of Scientific Computing, 1998, 13(1):105-114. |