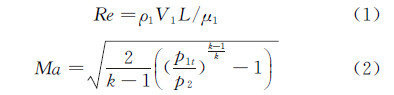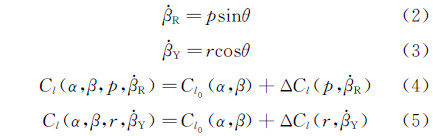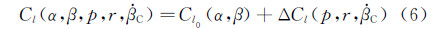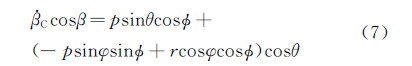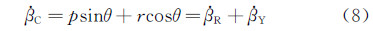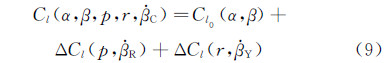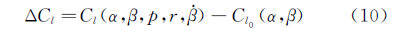飞机大迎角下的高机动性是现代战斗机的一项重要战术指标,这就要求飞机设计人员能够提供足够准确的大迎角机动飞行中的非定常空气动力数据。由于飞机机动飞行的运动过程很复杂,在风洞中准确模拟飞机机动飞行并测量其气动力显得十分重要。对于简单的机动飞行,如眼镜蛇机动[1, 2]、机翼摇滚[3, 4]等,风洞模拟相对容易,目前国内外许多风洞已经设计了实验装置并进行了一系列的实验[5, 6, 7, 8]。而对于复杂的机动飞行,如Herbst机动[9]等,飞机在大迎角状态下为同时绕几个轴的耦合运动。实际上,Herbst机动就是飞机在快速拉起到大迎角时进行无侧滑或小侧滑状态下的偏航与滚转耦合运动,这类机动飞行方式很有实战意义。事实上,有些飞行力学的研究者也提出了同样的研究课题,例如美国的Zhongjun W[10]等人在F-16XL飞机的飞行特性模拟计算与飞行实验结果的对比时,提出了需要获得横航向耦合运动非定常空气动力参数的必要性。在国内,南京航空航天大学的黄达[11, 12]等人在偏航-滚转耦合运动的非定常气动力特性研究中做了大量卓有成效的工作,在这些文献中主要定性地研究了耦合运动与单自由度运动的迟滞特性的异同。本文将在此研究的基础上,从单自由度的气动力时间历程效应分析出发,通过适当的实验方案设计,尝试在耦合运动和单自由度运动的各状态变量一致的情况下,定量地研究耦合特性的具体影响量,并得到更加可靠的结论,为耦合运动的非定常气动力建模提供依据。
1 实验设备和模型 1.1 双自由度大幅振荡机构本次实验是在中航工业空气动力研究院FL-8回流式闭口低速风洞中进行的,风洞实验段长5.5m,截面尺寸3.5m×2.5m,空风洞最大风速72m/s。动态实验平台为新改造设计的双自由度大幅振荡实验系统。图 1为双自由度振荡系统结构,模型正装时液压马达驱动弯刀使模型做俯仰运动,而当模型侧装时即可实现偏航振荡运动,伺服电机能够驱动模型做滚转振荡,运动过程中,模型的实际迎角和侧滑角可以通过机构角转换得到。
 |
| 图 1 双自由度振荡系统结构示意图 Fig 1 Structure diagram of coupling oscillation system |
式中:θ为平台转盘角,φ为大弯刀转角,而Φ是尾撑支杆滚转角。图 2为某飞机大幅振荡实验照片,模型采用尾撑。
 |
| 图 2 大幅振荡实验照片 Fig 2 Picture for large amplitude oscillation test |
实验采用动态专用六分量内式天平,天平测得的电信号由FL-8风洞VXI采集系统采集,数字信号由工控机处理,实验原始数据由大幅振荡实验处理程序处理成体轴六分量系数。动态滤波采用傅里叶变换数字滤波器,实验现场可以实时显示曲线。
2 实验结果和分析 2.1 时间历程影响研究考虑到模型在大振幅强迫振荡时,其姿态角及角速率始终在变化中,为了获得单纯的时间历程影响,需保证这些状态变量都一致,而仅仅运动历程不同。现以单自由度滚转振荡的滚转力矩系数为例加以说明。为了研究时间历程的影响,本文进行了表 1中所描述状态的滚转振荡试验,需要说明的是表 1中分别在10°、20°、30°及40°共4个振荡平衡位置迎角处各自进行4个不同振幅和频率的振荡实验,总共有16次实验。从表 1可知,在每个振荡平衡位置迎角处,不同振幅、频率组合状态下,迎角、侧滑角、滚转角及滚转角速度等位移和运动速度变量均相同,唯一不同的是其前一时间段位移和运动速度,即时间历程不同,因而模型在振荡平衡位置处的前一时刻气动力特性不同。基于此,通过分析各振荡平衡位置迎角处不同运动状态的气动力特性差异就可以研究在不同迎角范围气动力的时间历程影响。图 3~6给出了不同振荡平衡位置迎角处的时间历程影响实验结果。在图 3和4中,静态气动力系数曲线基本在动态迟滞环中间,且随着位移向平衡位置靠近,非定常气动力增量逐渐变大,且各运动状态在振荡平衡位置处非定常气动力增量基本相等,又因为平衡位置处各运动状态的位移和运动速度矢量相同,因此,在小迎角时滚转振荡运动的时间历程影响较小。这可能是因为在小迎角下,虽然左右机翼翼面流场结构的变化相对于翼面本身的运动仍然存在迟滞现象,但对于前机身带边条翼的战斗机布局在较小迎角处流场始终是脱体涡结构,没有出现涡的破裂,因而非定常气动力增量仅是角速度引起的,并不会出现非线性迟滞增量,所以在振荡平衡位置处滚转角速度相同时时间历程的影响较小。然而,如图 5和6所示,振荡平衡位置迎角在30°和40°时,静态气动力曲线并不在动态迟滞环中间,甚至跳出了迟滞环。且各运动状态下,非定常气动力增量差值明显,又因为平衡位置处位移和运动速度等变量相同,因而时间历程对气动特性的影响显著增大。原因可能是:30°迎角后,在大幅滚转振荡过程中,左右机翼的当地迎角跨度较大且经过失速迎角区域,此时机翼表面流场不仅相对于翼表本身运动迟滞,而且流场结构也在发生变化,这种脱体涡的破裂与再附的迟滞将会引起极大的非线性非定常气动力增量。需要说明的是,图 6中由于各状态下的气动力迟滞环出现交叉,因而振荡平衡位置处非定常气动力增量的差别没有图 5中明显,但由于各自交叉次数不同,在振荡平衡位置处迟滞环方向就不同,即滚转阻尼特性不同,说明此时运动历程的影响可能更复杂。
| 振荡平衡位置迎角 | 振幅 | 频率 | 振荡模态 |
| 10°~40° | 40° 20° 13° 10° | 0.4Hz 0.8Hz 1.2Hz 1.6Hz | 滚转振荡 |
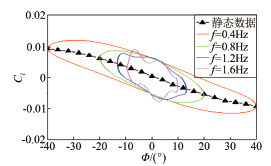 |
| 图 3 滚转运动在平衡位置为迎角10°时的时间历程影响 Fig 3 The time history influence at equilibrium position of α=10° for roll oscillation |
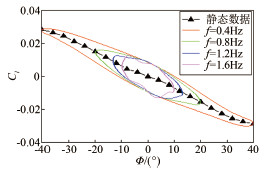 |
| 图 4 滚转运动在平衡位置为迎角20°时的时间历程影响 Fig 4 The time history influence at equilibrium position of α=20° for roll oscillation |
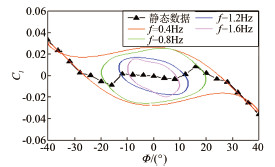 |
| 图 5 滚转运动在平衡位置为迎角30°时的时间历程影响 Fig 5 The time history influence at equilibrium position of α=30° for roll oscillation |
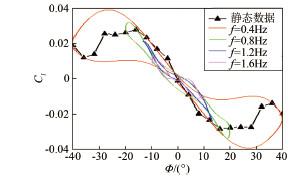 |
| 图 6 滚转运动在平衡位置为迎角40°时的时间历程影响 Fig 6 The time history influence at equilibrium position of α=40° for roll oscillation |
偏航振荡运动和耦合运动的时间历程影响和滚转运动类似,如图 7所示,给出了偏航振荡运动在振荡平衡位置迎角30°时的历程影响曲线。
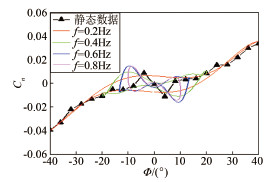 |
| 图 7 偏航振荡运动在平衡位置为迎角30°时的时间历程影响 Fig 7 The time history influence at equilibrium position of α=30° for yaw oscillation |
本次实验在模型振荡平衡迎角0°~90°范围内开展研究,单自由度滚转振荡、偏航振荡及偏航-滚转耦合振荡的振幅均为40°、频率相同,这样在振荡平衡位置处耦合运动与相应的单自由度运动的状态变量相同,不同的是时间历程和耦合因素,表 2给出了各振荡模态的实验参数变量,2.1节已经分析了各运动模态的时间历程影响,现只需对比耦合运动与单自由度运动气动力,便可比较直观地研究双自由度运动中耦合因素的影响。
| 振荡平衡位置迎角 | 振幅 | 频率 | 振荡模态 |
| 0°~90° | 40° | 0.2Hz 0.4Hz 0.6Hz 0.8Hz | 滚转/偏航/偏航 -滚转耦合振荡 |
先引入几个简单的气动力模型表达式并以滚转力矩系数为例加以说明。忽略角加速度的影响,仅考虑迎角α、侧滑角β、侧滑角速率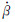 及滚转角速度p和偏航角速度r的影响。单自由度滚转振荡时,将振荡平衡位置的滚转力矩系数分解为静态气动力矩及由滚转角速度和侧滑角速率
及滚转角速度p和偏航角速度r的影响。单自由度滚转振荡时,将振荡平衡位置的滚转力矩系数分解为静态气动力矩及由滚转角速度和侧滑角速率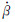 引起的增量;而单自由度偏航振荡时,相应地分解为静态气动力矩及由偏航角速度r和侧滑角速率
引起的增量;而单自由度偏航振荡时,相应地分解为静态气动力矩及由偏航角速度r和侧滑角速率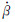 引起的增量。不论是单自由度滚转振荡,还是单自由度偏航振荡,其
引起的增量。不论是单自由度滚转振荡,还是单自由度偏航振荡,其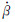 不是独立的,且分别和p、r相关,在振荡运动的平衡位置处相关公式如下:
不是独立的,且分别和p、r相关,在振荡运动的平衡位置处相关公式如下:
上式中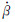 R和
R和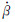 Y分别是滚转和偏航振荡的侧滑角速率。公式(4)和(5)分别表示滚转振荡和偏航振荡运动中的滚转力矩系数公式,其中Cl0(α,β)表示对应姿态角下的静态气动力。相应地,耦合振荡运动时,表达式如下:
Y分别是滚转和偏航振荡的侧滑角速率。公式(4)和(5)分别表示滚转振荡和偏航振荡运动中的滚转力矩系数公式,其中Cl0(α,β)表示对应姿态角下的静态气动力。相应地,耦合振荡运动时,表达式如下:
公式(6)中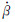 C表征耦合振荡平衡位置处的侧滑角速率,对公式(1)中的第2式求导可得:
C表征耦合振荡平衡位置处的侧滑角速率,对公式(1)中的第2式求导可得:
在耦合振荡运动的平衡位置处,β=0、Φ=0且φ=0,则公式(7)简化为:
从公式(8)中可知,在振荡平衡位置处,耦合运动的侧滑角速率等于各单自由度振荡运动侧滑角速率的线性叠加。在耦合运动的平衡位置处,绕体轴的角速度p、r及侧滑角速率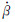 均等于单自由度相应变量的线性叠加。
均等于单自由度相应变量的线性叠加。
若耦合振荡气动力特性也是线性叠加的,则振荡平衡位置的滚转力矩元表达式如下:
单自由度及耦合振荡运动的平衡位置姿态角α和β相同,则Cl0(α,β)理论上应该相等,这里令:
比较表达式(6)和(9)中该滚转力矩系数差量ΔCl随迎角α的变化规律。实验结果在图 8(a)中给出。
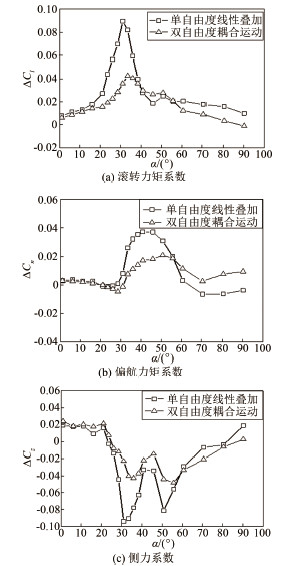 |
| 图 8 耦合运动与单自由度叠加气动力特性比较 Fig 8 Comparison of unsteady aerodynamic between coupling movement and sum of single degree of freedom movements |
图 8(a)中对应的各模态振荡频率均为0.6Hz且振幅为40°时,图中横坐标的迎角是各振荡运动平衡位置处的迎角。在20°迎角前,耦合运动滚转力矩系数几乎等于单自由度运动相应系数的线性叠加,由前时间历程的影响分析可知,在此迎角范围内,不同历程的影响较小。因此,在小迎角时,对于偏航-滚转耦合运动,耦合因素并没有带来滚转气动力系数的变化。这可能是因为:在小迎角耦合运动过程中,左右机翼的当地迎角跨度不大,翼面的脱体涡流虽然相对于运动本身有迟滞,但流场结构并没有发生变化,这时气动力动态增量仅仅与位移矢量和运动速度相关,在振荡平衡位置处,耦合运动的位置矢量和速度矢量等于各单自由度运动的线性叠加,因而滚转气动力模型完全可以分解成相应的单自由度运动气动力模型的线性叠加。当迎角达到20°后,随着迎角的增加,耦合运动滚转力矩系数增量与单自由度运动叠加的差值愈来愈大,在30°~35°迎角附近,耦合运动滚转力矩系数动态增量大小与相应单自由度运动叠加相差最大。这可能是因为:振荡平衡位置迎角达到30°后,在耦合运动过程中,左右机翼当地迎角在失速迎角附近变化,其表面涡流结构在后缘处出现涡破裂,这种涡的破裂和再附的迟滞将带来极大的非定常气动力增量,且该增量不仅与飞机的运动位置矢量和速度矢量相关,还和时间历程及耦合因素紧密相关,因而即使在振荡平衡位置处耦合运动和各单自由度运动的位置矢量、速度矢量相等,其非定常气动力增量仍然存在较大差值。上述分析说明,在失速迎角附近的中等迎角处,由于其时间历程及耦合特性影响显著,耦合运动已经不能简单地分解成相应的单自由度运动叠加。因此,此时在建立非定常气动力模型时不仅仅需要考虑各单自由度运动的气动力模型,还需要添加耦合项的综合影响。迎角40°后,随着迎角的增加,耦合运动滚转力矩系数动态增量大小与相应单自由度运动叠加的差值虽有变小,但仍然较大,特别是当迎角达到60°后趋于一个稳定差值。这说明在远超失速迎角的范围,飞机运动的时间历程及耦合特性影响仍然较大。图 8(b)和(c)中描述的偏航力矩系数与侧力系数的变化规律和滚转力矩系数类似。
3 结论本文的研究结论主要有以下2点:
(1) 对于单自由度滚转振荡,小迎角时,滚转力矩受时间历程影响较小。因此,此时的气动力模型只需考虑飞机的瞬时运动状态变量;而在30°迎角后,其受时间历程的影响显著。单自由度偏航振荡,其时间历程的影响规律类似。
(2) 在20°迎角前,耦合运动横航向力矩模型完全可以分解成相应的单自由度运动气动力模型的线性叠加;在失速附近的中等迎角区域,运动耦合及时间历程对力矩特性影响显著;而在60°后的大迎角区域,耦合的影响虽然减小,但仍然很大。
本文虽然对偏航-滚转耦合运动非定常气动力增量与各单自由度运动的增量线性叠加进行了比较,并分析了可能的原因,但也仅仅是气动力结果,下一步工作还需对耦合运动过程中的流场结构机理开展研究,特别是涡破裂点的变化规律研究。
| [1] | 李中华. Su-27飞机眼镜蛇机动及其战术意义[J]. 飞行力学, 2000, 18(1):54-57. Li Z H. Su-27 Cobra maneuver and its tactical application[J]. Flight Dynamics, 2000, 18(1):54-57. |
| [2] | 高慧琴, 高正红. 典型过失速机动运动规律建模研究[J]. 飞行力学, 2009, 27(4):9-13. Gao H Q, Gao Z H. Motion modeling of typical post stall maneuvers[J]. Flight Dynamics, 2009, 27(4):9-13. |
| [3] | Ericsson L E. Wing rock generated by forebody vortices[R]. AIAA-87-0268, 1987. |
| [4] | Pelletier Alain. Dynamic behavior of an 80/65 double-delta wing in roll[R]. AIAA-98-4353, 1998. |
| [5] | Brandon J M, Shah G H. Unsteady aerodynamic characteristics of fighter model undergoing large-amplitude pitching motions at high angles of attack[R]. AIAA-90-0309, 1990. |
| [6] | Jay M Brandon, Mark A. Overview of dynamic test techniques for flight dynamics research at NASA LaRC(Invited)[R]. AIAA-2006-3146, 2006. |
| [7] | William J G. AFRL F-22 dynamic wind tunnel test result[R]. AIAA-99-4015, 1999. |
| [8] | 卜忱, 杜希奇, 黄丽婧, 等. 旋转流场下飞机大幅滚转振荡时的动态横向气动特性实验研究[J]. 实验流体力学, 2008, 22(1):46-50. Bu C, Du X Q, Huang L J, et al. Investigation of unsteady aerodynamic characteristics for the large amplitude rolling under rotary flow field[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1):46-50. |
| [9] | Michael C, Francis S. X-31 enhanced fighter maneuverability demonstrator fight test achievements[R]. ICAS-94-72, 1994. |
| [10] | Zhongjun W, Edward C L. Unsteady aerodynamic effects on the flight characteristics of a F-16XL configuration[R]. AIAA-2000-39, 2000. |
| [11] | 黄达, 吴根兴. 飞机偏航-滚转耦合运动非定常空气动力实验[J]. 南京航空航天大学学报, 2005, 37(4):408-411. Huang D, Wu G X. Experiment on fighter oscillating in large amplitude yaw-roll motion[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2005, 37(4):408-411. |
| [12] | 黄达. 飞行器大幅振荡运动非定常空气动力特性研究[D]. 南京:南京航空航天大学, 2007. Huang D. Unsteady aerodynamic characteristics for the aircraft oscilation in large amplitude[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2007. |