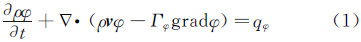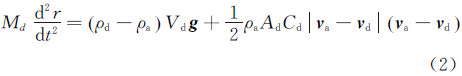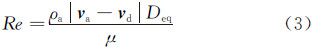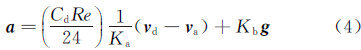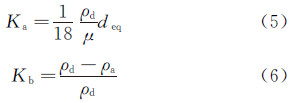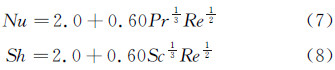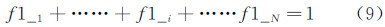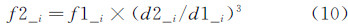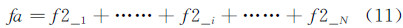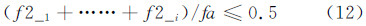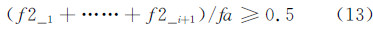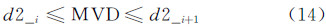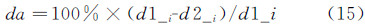飞机在穿越含有过冷水滴(温度低于冰点但仍保持液态的水滴)的云层时,云层中的过冷水滴碰撞在飞机表面,在碰撞区域及其附近就会发生结冰[1]。飞机结冰是飞行实践中广泛存在的一种现象,也是造成飞行安全事故的主要隐患之一[2, 3]。结冰风洞试验是进行结冰研究的主要手段,其通过在风洞内制造结冰气象条件,对真实结冰现象进行模拟[4, 5]。为了模拟结冰过程,结冰风洞内需要配备制冷系统和喷雾系统,用于产生过冷水滴。其中喷雾系统是结冰风洞的核心组成部分,喷雾系统性能的高低、喷雾系统与结冰风洞气动外形和流场品质的匹配性以及喷雾系统对应使用手册的完善程度等,都是衡量结冰风洞性能和水平的主要指标。
结冰风洞的喷雾系统主要由供水系统、供气系统、喷嘴及安装喷嘴的喷雾耙等组成,喷雾耙安装于风洞稳定段的入口。水滴由施加一定压力的水、气混合雾化产生,通过喷嘴喷出,并随风洞内的气流一起运动至试验段。为了防止喷嘴堵塞,雾化的水通常需要加热,这使得喷出的水滴不仅与周围气流有较大的速度差,还有很大的温度差别,水滴在运动过程中将与周围冷空气间进行强烈的传质传热,不但其温度不断降低,而且由于蒸发,水滴直径也会减小。针对这种现象,在研究结冰风洞喷雾系统特性时,有2个问题需要关注:一是经过运动及蒸发之后,喷嘴出口处喷雾粒子的正态分布特性在试验段是否能够保持,二是由于蒸发导致试验段水滴的容积平均直径(Medium Volume Diameter,简称MVD)与初始MVD有多大差异。在结冰风洞试验段直接进行不同状态粒子分布特性的测量,会耗费巨大的成本,而且由于制冷和喷雾的双重作用,风洞运行时视窗易模糊,制约了测量精度。另外,在喷雾系统设计阶段,进行风洞内的直接测量也不现实。因此,有必要发展可行的方法,研究结冰风洞试验段粒子的分布特性。
在国外,针对不同结冰风洞的本身性能和技术指标,相关机构均投入了较大力量研究其喷雾系统的特性,以美国NASA的结冰风洞IRT和意大利CIRA的结冰风洞IWT为例,都开展了一系列研究,这些研究多集中于采用试验[6, 7, 8, 9, 10]或计算[11]的方法研究风洞试验段的云雾均匀性分布,对喷雾粒子蒸发及其影响关注较少。国内在该领域开展的工作有限,主要集中于结冰风洞喷嘴性能测试[12, 13]、水滴运动及传热传质仿真[14, 15]等。
本文在前期研究的基础上[12, 13, 14],采用实验测试和数值计算相结合的方法,对结冰风洞试验段水滴的分布特性进行研究,通过搭建独立的喷雾粒子试验系统,得到喷嘴出口处的粒子分布特性。在此基础上,采用数值计算的方法计算不同水滴在风洞内的运动及传质传热过程,进而获得试验段粒子的分布特性。
1 喷雾粒子的实验测试方法 1.1 喷雾粒子实验系统喷雾粒子实验系统如图 1所示,主要由供水装置、供气装置和喷嘴测试平台3部分组成。使用一台离心泵为喷嘴供应去离子水,使用氮气瓶组为喷嘴供气,水压和气压均可自动调节,水压及气压调节范围为0.03~1.2MPa,压力调节精度0.005MPa。
 |
| 图 1 喷雾粒子实验系统 Fig 1 The experimental system for spraying droplets |
喷嘴测试平台如图 2所示,由试验台本体、真空抽气系统及控制系统组成。其主要性能如下:试验台容积为2m3,由水环真空泵配合一个补气阀门精确控制真空度,真空泵抽速为40L/s,压力调节范围为30~100kPa,压力控制精度为0.5kPa。
 |
| 图 2 喷嘴测试平台 Fig 2 The nozzle test platform |
结冰风洞所使用的空气助雾化喷嘴如图 3所示,喷嘴安装在喷嘴测试平台上,喷嘴出口水滴粒子分布主要决定于喷嘴结构、雾化的水压pw和气压pa。为增强喷嘴的雾化效果,水、气在喷出之前首先在混合室进行预混,从而可获得更细微的水滴颗粒。
 |
| 图 3 结冰风洞所使用的空气助雾化喷嘴 Fig 3 The air-assisted atomization nozzle of icing wind tunnel |
使用PDI(相位多普勒干涉仪)对粒子的粒径、速度及分布进行测量。PDI是PDPA基础上的新一代相位多普勒颗粒分析系统,可以在不同的应用环境中实现对单个颗粒粒径大小以及三维速度的实时无接触测量。设备构成主要包括光学发射探头、光学接收探头、ASA信号处理器以及自动设备管理系统。采用前向散射原理对雾化颗粒进行测量,镜头组合为500mm(发射)×400mm(接收),发射和接收镜头的安装方法和相对位置如图 4所示。对于水滴这样的透明介质来说,采用前向散射的测量方法获得的信噪比高,更易获得较高的粒子通过率和有效粒子数量,能有效提高粒径测量的准确度。
 |
| 图 4 PDI镜头的安装方法 Fig 4 The PDI lens assembly method |
在进行喷嘴的粒径特性测量时,测点位置位于距喷嘴出口约200mm的中心线上。在距喷嘴出口200mm至更远的距离上,雾化颗粒随距离的变化已不再明显,说明在这一距离上,水滴已经完全雾化。在喷雾横截面上,径向测点与中心测点上的雾化颗粒的直径差别约为5.5%~7.5%,粒度分布较为均匀,同时,从边缘到中心点上,雾化水滴的液态水含量也呈现逐渐升高的趋势,因此,选择中心点作为衡量喷嘴雾化特性的测量点具有较强的代表性。
2 粒子运动及传热传质过程计算方法 2.1 空气流场计算方法结冰风洞内水滴运动和传质传热特性计算 ,是在获得风洞的空气流场分布基础上进行的。本文采用CFD方法计算空气流场分布,流场计算的控制方程为写成输运方程形式的时均N-S方程,其通用形式为:
式中:φ为输运变量,ρ为空气密度,v为空气速度,Γφ为扩散系数,qφ为源项,φ、Γφ和qφ取不同的值,可代表空气的连续性方程、动量方程和其他标量(如湍流耗散率等)的输运方程。方程中各项的物理意义及具体表达式,以及方程的离散求解方法,可参见文献[16],此处不再详述。
2.2 水滴运动计算方法在得到空气流场速度分布的基础上,本文采用拉格朗日法计算水滴运动轨迹。由牛顿第二定律,直角坐标系中,水滴运动方程可以写成[16]:
式中:Md是水滴质量,Ad是水滴的迎风面积,Vd是水滴体积,Cd是阻力系数,ρd是水滴密度,ρa是空气密度,r 是水滴的位置矢量,g 是重力加速度矢量,v a为空气速度,v d为水滴速度。
定义相对雷诺数Re,其表达式为
式中:Deq为水滴直径,μ为空气的粘性系数,则式(2)可写成如下形式:
式中: a 为水滴运动的加速度,Ka、Kb的表达式分别为
完成流场计算得到空气速度之后,方程(4)成为常微分方程,本文采用一阶欧拉法对其进行数值积分求解。
2.3 传质传热特性计算方法水滴表面附面层中的无因次温度梯度可用Nu数表示,无因次浓度梯度可用Sh数表示。空气流场速度分布、水滴轨迹及速度计算完成之后,本文采用Ranz和Marshall给出的公式[14]计算Nu数,再根据传热和传质的比拟计算Sh数。
3 蒸发后MVD的计算方法通常用水滴容积平均直径MVD来表征喷雾粒子的大小,MVD定义为将总水量等分成两半的临界尺寸,即认为直径大于MVD的大水滴的总体积与直径小于MVD的小水滴的总体积相等。根据MVD的定义,对于某种给定分布的结冰云雾(水滴簇),我们只需要找到一种尺寸,使得大于这种尺寸的水滴总质量与小于这种尺寸的水滴总质量相等,则该尺寸就是给定结冰云雾的MVD。因此,根据原始分布计算蒸发后水滴簇MVD的方法为:
设原始喷雾产生的水滴簇包含N种直径,其分布为水滴直径d1_i,质量比例f1_i,很明显:
设蒸发之后的水滴直径为d2_i,质量比例(相对于液态和气态水的总质量)为f2_i,则有:
令:
如果:
并且
则有:
在d2_i和d2_i+1间进行插值,即可得到MVD的值。
根据以上计算方法可知,要计算蒸发之后的MVD,需要以下 输入量:(1) 蒸发之前喷雾粒子的分布,包括水滴直径d1_i及其对应的质量比例f1_i;(2) 蒸发之后水滴的直径d2_i,蒸发之后的质量比例f2_i可以根据d1_i、f1_i和d2_i由式(10)计算获得。其中,d1_i和f1_i取决于喷嘴的特性以及雾化时的水压和气压,由PDI测试得到,d2_i决定于风洞内的流动条件,不同流动环境和条件对应的d2_i也不同。因此,为了获得蒸发之后的MVD,必须在获得初始喷雾直径的基础上,计算不 同条件下的蒸发后直径d2_i。
4 结冰风洞试验段粒子MVD特性分析 4.1 典型喷雾粒子测试首先采用PDI测试了典型状态下雾化水滴的速度、数量和质量分布。喷嘴雾化的条件为:水压pw=0.403MPa,气压pa=0.25MPa。
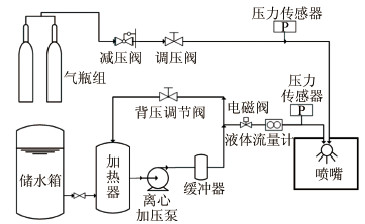
图 5给出了不同直径雾化水滴的速度分布,可以看到,雾化水滴的直径在0~65μm之间,大部分水滴直径小于30μm,雾化水滴的速度主要分布于-2~4m/s的区间,最大不超过6.5m/s。
 |
| 图 5 雾化水滴的速度分布 Fig 5 Velocity distribution of spraying droplets |
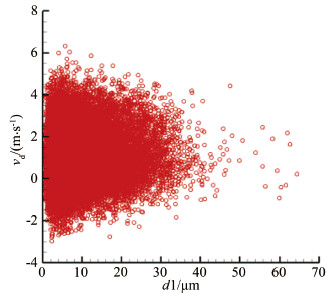
图 6给出的是不同直径雾化水滴的数量分布,直径越小的水滴,其数量越多。图 7给出的是不同直径水滴的质量占比,根据MVD的定义,可以计算出该分布的MVD值为22.3μm。图 7表明,水滴质量占比呈近似正态分布,质量占比最高的是直径在22μm左右的水滴,这是由于水滴数量随着直径增加而减少,小直径的水滴虽然数量多,但其质量小,大直径的水滴虽然质量大,但其数量小,因此与MVD值接近的水滴占有高的质量比例。
 |
| 图 6 雾化水滴的数量分布 Fig 6 Amount distribution of spraying droplets |
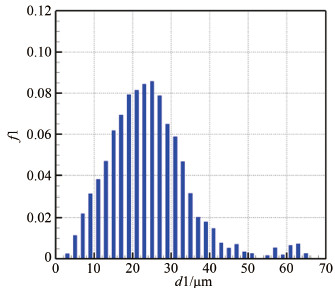 |
| 图 7 雾化水滴的质量分布 Fig 7 Mass distribution of spraying droplets |
给出喷雾水滴的初始分布之后,采用数值方法对水滴在结冰风洞内的运动和传质传热情况进行计算,进而得到结冰风洞试验段内水滴的分布特性。
计算构型如图 8所示,由某试验段截面为3m×2m结冰风洞的稳定段、收缩段和扩散段组成,水滴从喷嘴喷出,经过收缩段最后运动到试验段。
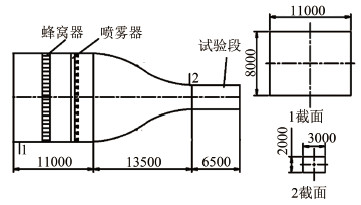 |
| 图 8 计算构型 Fig 8 Computational configuration |
计算条件为:收缩段入口截面气流温度T_air=-15℃,试验段风速v=120 m/s,收缩段入口截面相对湿度RH=70%、100%,水滴初始温度T_water=40℃,收缩段入口总压p0=0.534×105Pa。
表 1和2分别给出了湿度为70%和100%时,喷雾粒子的初始直径及其运动到结冰风洞试验段时的直径。图 9和10给出的是2种湿度条件下不同直径水滴运动到试验段的直径变化率da,da定义为由于蒸发导致的水滴直径变化的百分比,即
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| d 1/μm | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| d 2/μm | 0 | 8.0 | 20.5 | 31.0 | 41.0 | 50.8 | 60.5 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| d1/μm | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| d2/μm | 4.7 | 14.3 | 23.8 | 33.4 | 42.9 | 52.4 | 62.0 |
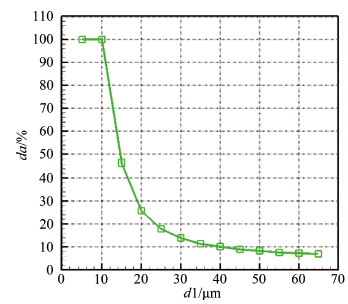 |
| 图 9 蒸发后水滴直径变化率(相对湿度70%) Fig 9 Change ratio of droplet diameter after evaporation (Relative humidity is 70%) |
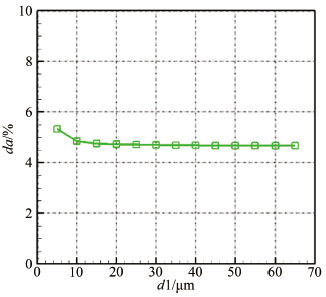 |
| 图 10 蒸发后水滴直径变化率(相对湿度100%) Fig 10 Change ratio of droplet diameter after evaporation (Relative humidity is 100%) |
计算结果表明:(1) 水滴在非饱和空气中运动的蒸发量远大于饱和空气中水滴的蒸发量;(2) 湿度为70%时,水滴在运动过程中有比较明显的蒸发,水滴直径越小,其直径变化率越大,初始直径小于10μm的水滴运动到试验段之前已经全部蒸发完毕,直径变化率达100%,最大的水滴由于蒸发,其直径将由65μm减小至60.5μm,直径变化率为7%;(3)空气湿度为100%时,水滴在运动过程中也伴随着蒸发过程,随着水滴直径的增加,蒸发后水滴直径的绝对变化量也增加,值得注意的是,不同水滴的直径变化率接近,在4.7%左右。
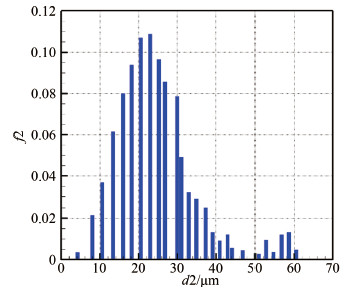
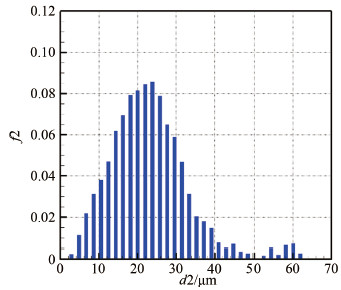
4.3 典型状态结冰风洞试验段粒子的MVD特性根据实验测试的喷雾水滴初始分布以及计算获得的水滴运动过程中的传热传质特性,可以得到结冰风洞试验段水滴的分布,进而由式(10) ~(14)得到试验段水滴的MVD。图 11给出的是湿度为70%时试验段不同直径水滴的质量分布,此时的MVD为22.6μm,比初始的MVD略高;图 12给出的是湿度100%时试验段水滴的质量分布,对应的MVD值为21.2μm,略小于初始的MVD。
 |
| 图 11 试验段水滴的质量分布(相对湿度70%) Fig 11 Mass distribution of droplets in the test section (Relative humidity is 70%) |
 |
| 图 12 试验段水滴的质量分布(相对湿度100%) Fig 12 Mass distribution of droplets in the test section (Relative humidity is 100%) |
可以发现:(1)与初始水滴分布类似,试验段的水滴也保持了近似的正态分布;(2)虽然空气越不饱和,水滴蒸发越明显,但湿度为100%时试验段水滴的MVD反而比湿度为70%时小,这主要是因为在空气不饱和时,很多小水滴已经全部蒸发成气体,使得剩下水滴簇的MVD不降反升;(3)无论空气饱和与否,试验段的MVD与初始MVD都很接近,需要注意的是,虽然蒸发不能引起明显的MVD变化,但会导致风洞内的液态水含量减小。
5 结论采用实验测试和数值计算相结合的方法,对结冰风洞试验段水滴的MVD特性进行了研究,对比了空气饱和与不饱和状态的影响,得到如下结论:
(1) 喷嘴出口处的初始喷雾粒子与试验段的水滴均保持近似正态的分布,直径与MVD值接近的水滴占有高的质量比例;
(2) 无论空气是否饱和,喷雾水滴在结冰风洞内运动时都会发生蒸发现象,导致水滴直径减小,但试验段的MVD与初始MVD接近,蒸发不能引起明显的MVD变化;
(3) 由于空气不饱和时,很多小水滴已经全部蒸发成气体,使得剩下水滴簇的MVD不降反升,因此湿度为100%时试验段水滴的MVD反而比湿度为70%时小;
(4) 采用本文提出的实验测试和数值计算相结合的方法研究冰风洞试验段水滴的分布特性,可有效弥补在风洞内进行直接试验测试的不足,为结冰风洞的设计和调试提供技术支撑。
| [1] | Cebeci T, Kafyeke F. Aircraft icing[J]. Annual Review of Fluid Mechanics, 2003, 35:11-21. |
| [2] | Frank T Lynch, Abdollah Khodadoust. Effects of ice accretions on aircraft aerodynamics[J]. Progress in Aerospace Sciences, 2001, 37(8):669-767. |
| [3] | Bragg M B, Broeren A P, Blumenthal L A. Iced-airfoil aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41(5):323-362. |
| [4] | Soeder R H, Sheldon D W, Robert F S, et al. NASA glenn icing research tunnel user manual[R]. NASA/TM-2003-212004, 2003. |
| [5] | Kind R J, Potapczuk M G. Experimental and computational simulation of in-flight icing phenomena[J]. Progress in Aerospace Science, 1998, 34:275-345. |
| [6] | Thomas B I, John R O. New icing cloud simulation system at the NASA Glenn research center icing research tunnel[R]. AIAA-98-0143, 1998. |
| [7] | Leone G, Vecchione L. The new CIRA icing wind tunnel spray bar system development[R]. AIAA-2000-0629, 2000. |
| [8] | Robert F I. Icing cloud calibration of the NASA Glenn icing research tunnel[R]. AIAA-2001-0234, 2001. |
| [9] | Robert F I. Comparison of liquid water content measurement techniques in an icing wind tunnel[R]. NASA/TM-1999-209643, 1999. |
| [10] | Robert F I. 2006 icing cloud calibration of the NASA Glenn icing research tunnel[R]. NASA/TM-2006-215177, 2006. |
| [11] | Bhargava C, Loth E, Potapczuk M. Numerical simulation of icing clouds in the NASA glenn icing research tunnel[J]. Journal of Aircraft, 2005, 42(6):1442-1451. |
| [12] | 符澄, 彭强, 张海洋, 等. 结冰风洞喷嘴雾化特性研究[J]. 实验流体力学, 2015, 29(2):32-36. Fu C, Peng Q, Zhang H Y, et al. The atomization characteristics research for spray nozzle of icing wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(2):32-36. |
| [13] | 符澄, 彭强, 张海洋, 等. 结冰风洞环境对喷嘴雾化特性的影响初步研究[J]. 实验流体力学, 2015, 29(3):30-34. Fu C, Peng Q, Zhang H Y, et al. Preliminary research on spray nozzle atomization characteristics in icing wind tunnel environment[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(3):30-34. |
| [14] | 易贤, 马洪林, 王开春, 等. 结冰风洞液滴运动及传质传热特性分析[J]. 四川大学学报(工程科学版), 2012, 44(sup. 2):132-135. Yi X, Ma H L, Wang K C, et al. Analysis of water droplets movement and heat/mass transfer in an icing wind tunnel[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(sup. 2):132-135. |
| [15] | 蔡英磊, 董威. 冰风洞试验中水滴的传热传质计算研[J]. 航空发动机, 2013, 39(3):36-40. Cai Y L, Dong W. Calculation and analysis of heat and mass transfer for water droplet in icing tunnel test[J]. Aeroengine, 2013, 39(3):36-40. |
| [16] | 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳:中国空气动力研究与发展中心, 2007. Yi X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang:China Aerodynamics Research and Development Center, 2007. |