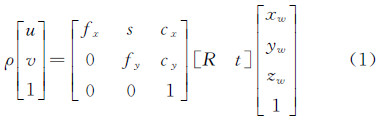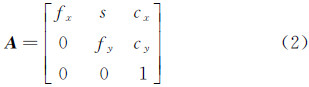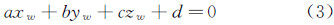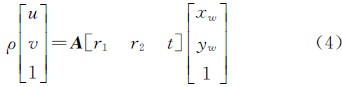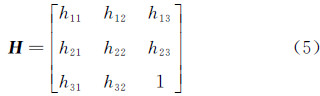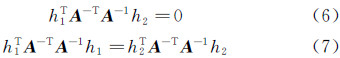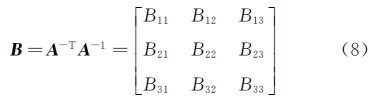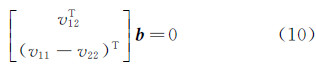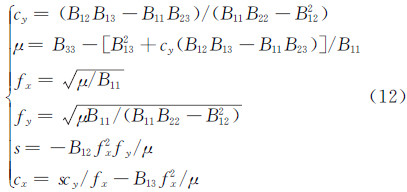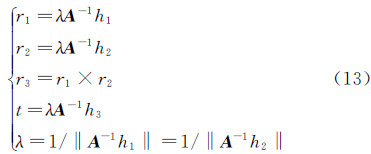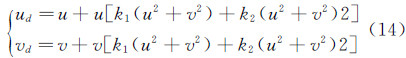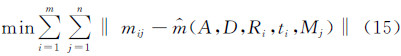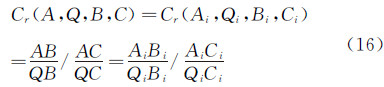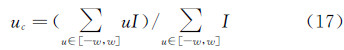2. 中国空气动力研究与发展中心, 空气动力学国家重点实验室, 四川 绵阳 621000;
3. 西南科技大学 信息工程学院, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China;
3. School of Information Engineering, University of Southwest Science and Technology, Mianyang Sichuan 621000, China
飞机穿过包含过冷水滴的云层时,表面容易结冰,使阻力增大、升力减小、临界迎角降低以及失速速度增大,给安全飞行造成极大危害[1, 2]。为确保飞行安全,非常有必要开展飞机结冰机理研究。目前,国内外学者已经从风洞试验、数值计算、传热过程等角度进行了结冰机理研究,并取得了一些研究成果[3, 4, 5, 6]。
在结冰风洞试验研究中,通常需要测量冰横截面轮廓,以判定结冰厚度和形状等重要信息。目前,广泛使用的冰横截面轮廓测量方法是热刀法,通过将铜质金属片加热后插入冰块,使冰块融化形成缝隙,在缝隙处插入标尺纸,使用铅笔或钢笔在标尺纸上描绘冰外部轮廓。这种接触测量方法存在的问题包括:首先,使用铅笔或钢笔手工描绘冰横截面轮廓容易破坏冰微小结构,无法得到精细化测量结果;其次,难以满足结冰生长过程冰形在线三维测量需求。研究表明,结冰冰形(厚度及形状)与液态水含量、平均水滴直径、温度、结冰时间、飞行速度和迎角等紧密相关[7, 8]。目前,为了探索结冰时间与结冰冰形之间的关系,通常需要多次试验,效率较低。此外,热刀法一次只能测量1个横截面,通过多次切割可以得到不同位置处冰形,但也难以得到精细的冰块三维形状。显然,精细化的冰块三维形状信息对提升结冰条件下飞机气动力CFD计算精度具有重要价值。因此,迫切需要可用于结冰生长过程冰形在线三维测量的方法。近期,国内外学者尝试了采用非接触测量方法进行冰横截面轮廓[9, 10]和三维形状半在线测量[11, 12]。中国空气动力研究与发展中心曾经尝试采用基于面结构光的三维扫描仪进行结冰外形扫描,但是,由于冰块表面反射系数低、透射系数高,需向冰块表面喷洒深色涂料,才能得到高对比度编码图案图像,极大地限制了该测量方法应用范围,也无法用于在线测量。与投影仪投射的编码条纹相比,激光器投射的线激光具有亮度集中、图像对比度高等优点,已被广泛应用于工业三维测量领域,无需向冰块喷洒深色涂料也可得到较好的观测图像。Hovenac等[9]采用线结构光测量冰轮廓,将线激光投射到冰块表面,用1台摄像机记录被冰块表面高低起伏调制变形的激光线条图像,根据激光线与摄像机之间的几何位置关系,计算激光线条位置处的冰块轮廓,并采用3组共面安置的线结构光测量设备实现了冰块完整轮廓测量。Zhang等[10]提出了相似的测量方法,即向冰块表面投射线激光,用2台摄像机拍摄激光线图像,通过立体视觉计算冰轮廓线三维测量结果。线结构光一次可测量一条轮廓线,与一维扫描装置配合,即可实现冰块三维形状扫描。比如,Hovenac等[9]等提出直接改变激光器方位进行扫描,Gong等[11, 12]采用转动棱镜改变激光方向进行三维扫描。
线结构光用于冰形在线三维测量的最大挑战是如何获得高对比度激光线图像,以及如何从冰面激光线图像中准确提取激光线位置。在风洞试验过程中,气流中的水滴、冰粒等引起激光能量衰减、降低激光线图像对比度,给冰面激光线位置提取造成极大困难。为得到高对比度冰面激光线图像,Gong等[11, 12]采用中波红外激光以增强激光穿透能力,并结合停止喷雾、冰面结霜等方法用于提升激光线条图像对比度,最终实现了结冰试验中半在线冰形三维测量。
作为结冰生长过程冰形在线三维测量前期探索性研究内容,本文设计基于线结构光的冰横截面轮廓测量简易装置,开发相关测量程序,并针对线结构光能量衰减而导致的激光线图像对比度低的问题,提出冰面激光中心线提取方法。对冰箱冻结的已知半径圆柱形冰块进行轮廓线测量精度评估测试;并对在中国空气动力研究与发展中心0.3m×0.2m结冰风洞中得到的二元翼型结冰冰块进行横截面轮廓测量,得到初步测量结果。
1 基于线结构光的冰横截面轮廓测量原理基于线结构光的冰横截面轮廓测量原理如图 1所示,激光器垂直投射面激光在冰面上,产生一束激光光条,激光光条受到冰面高度调制发生形变,摄像机以一定角度拍摄激光光条,采用图像处理方法提取激光光条中心线,并根据事先标定的激光平面与摄像机之间的几何位置关系计算激光光条中心线三维坐标,这些三维坐标在激光平面上的投影即为该光条处冰块横截面轮廓。
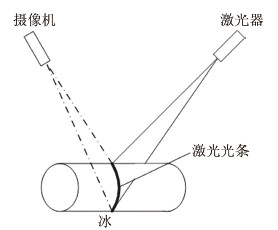 |
| 图 1 基于线结构光的冰横截面轮廓测量原理 Fig 1 Principle of ice cross sectional profile measurement with line structural laser |
采用图 2所示线面模型,可用于计算激光光条三维坐标,其中,ow-xwywzw是世界坐标系,由图 3所示标定板定义,其中,ow是棋盘格左上角顶点,xw、yw分别沿棋盘格水平、竖直方向,zw垂直于棋盘格平面,oc-xcyczc是摄像机坐标系,其中,oc是光心,zc与摄像机光轴重合,xc、yc垂直于光轴,u,v是图像坐标系。
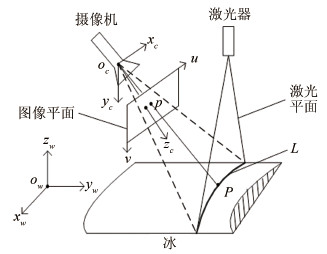 |
| 图 2 基于线面模型的激光线三维坐标计算 Fig 2 3D coordinates calculation of laser line based on line-surface model |
 |
| 图 3 用于激光平面标定的图像 Fig 3 Images used for laser plane calibration |
设激光光条L上任意一点P在图像平面上的投影为p,P的世界坐标为(xw,yw,zw),p的图像坐标为(u,v),它们之间满足:
式中:ρ是比例因子;fx、fy是u轴和v轴的等效焦距;cx、cy是光学中心;s是u轴和v轴的不垂直因子,一般情况下取s=0; R 是世界坐标系ow-xwywzw变换到摄像机坐标系oc-xcyczc的3×3旋转矩阵; t 是世界坐标系ow-xwywzw变换到摄像机坐标系oc-xcyczc的3×1平移矢量,R和t 为外部参数,描述了世界坐标系到摄像机坐标系间的变换关系;fx、fy、cx、cy、s为内部参数,令
作为内部参数矩阵。
线激光器投射出的激光平面在世界坐标系下的方程可描述为:
式中:(a,b,c,d)是激光平面方程系数。
给定摄像机投影方程(1)、激光平面方程(3)中系数,即可根据激光中心线上任意一点的图像坐标(u,v),计算其三维世界坐标(xw,yw,zw)。将三维世界坐标(xw,yw,zw)向激光平面投影,即可得到激光中心线上所有像素对应的冰块横截面轮廓。
2 线结构光测量系统标定当激光投射器与摄像机相对位置固定后,通过标定可确定摄像机投影方程(1)和激光平面方程(3)中的参数,以用于线结构光三维测量。
2.1 摄像机标定摄像机标定是通过一系列空间位置已知的参考点确定摄像机投影方程(1)中内外参数。典型的摄像机标定方法包括直接线形变换法[13]、RAC两步法[14]和张正友标定法[15],其中,张正友标定法[15]利用多幅不同视角位置的标定板(见图 4)上特征点的世界坐标与其图像上像点图像坐标间对应关系进行摄像机标定,具有使用简单和标定精度高等优点。本文采用基于张正友标定法的摄像机标定工具包[16]进行摄像机标定,并对摄像机拍摄图像进行非线性畸变修正。
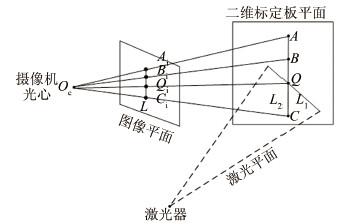 |
| 图 4 采用棋盘格基于交比不变性进行激光平面标定原理 Fig 4 Laser plane calibration principle based on cross ratio invariability using checkerboard |
张正友标定法分2步执行:第一步先利用理想的线性成像模型求出单应性矩阵 H ,并解出摄像机内部参数,然后运用内部参数和单应性矩阵 H 求出摄像机外部参数;第二步利用非线性成像模型求出径向畸变系数。
设定标定板上所有特征点的世界坐标zw=0,则摄像机投影方程(1)可简化为:
其中,A [r1 r2 t]为3×3矩阵,令 H = A [r1 r2 t]作为单应矩阵,并设
则h1,h2,h3]=A[r1,r2,t]。
因为r1,r2单位正交,则:
利用式(6)和(7)的约束条件,可计算出摄像机内部参数。
设:
其中,B 为对称矩阵,定义六维向量 b = [B11,B12,B22,B13,B23,B33] T,
则有:
其中,
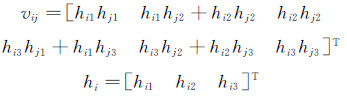
根据约束条件可得到关于 b 的2个齐次方程:
拍摄n幅标定板图像,可得到如下线性方程组:
式中: V 是一个2n×6的矩阵。如果n≥3,则可以列出6个以上的方程,从而可以解出一个带有比例因子的 b 。
求得了 b 即可得到矩阵 B ,进而即可求得摄像机的内部参数。假设μ为一个任意的比例系数,则有:
根据单应性矩阵 H 和内部参数 A ,可计算不同角度下摄像机的外参:
在实际应用中,一般摄像机的镜头并非理想的光学镜头,所以得到的图像坐标一般都会偏离理想的坐标,采用式(14)的2参数径向畸变模型对镜头畸变进行校正。
式中:ud,vd表示实际图像坐标,u,v表示理想图像坐标,k1,k2是径向畸变参数。给定n幅标定图像,每幅标定图像有m个点,则共有m×n个点,通过最小二乘可以得到径向畸变参数k1和k2的初始估计,令D=[k1,k2]作为径向畸变参数。
上述方法计算出的相机参数初值易受噪声干扰,为此采用最大似然估计对模型参数进行优化。设n图像中m×n个标定点的数据都被独立同分布的噪声所污染,给定如下目标函数:
式中: mij是第i幅图像中第j个标定点的图像坐标;A是摄像机内部参数;D是畸变参数;Ri和ti分别表示第i幅图像坐标系的旋转矩阵和平移向量;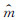 (A,D,Ri,ti,Mj)表示第i幅图像中的第j个标定点世界坐标Mj的图像坐标。式(15)运用LM(Levenberg-Marquardt)算法[17]可得到优化的摄像机参数。
(A,D,Ri,ti,Mj)表示第i幅图像中的第j个标定点世界坐标Mj的图像坐标。式(15)运用LM(Levenberg-Marquardt)算法[17]可得到优化的摄像机参数。
激光平面标定用于确定激光平面方程系数(a,b,c,d)。典型的激光平面标定方法有拉丝法、锯齿靶法和基于交比不变原理的二维靶标标定方法等[18],本文选用基于交比不变原理的二维靶标标定方法。在透视投影变换中,长度与长度之间的比例是可变的,但是长度比率的比值是不变的。如图 4所示,激光平面与二维标定板平面相交于直线L1,标定板上已知的3个棋盘格角点A、B、C构成直线L2,直线L1和L2的交点Q为激光平面上一个标定特征点。根据摄像机透视投影变换,直线L2在摄像机图像平面上的投影为直线L,4个共线点A、B、Q、C与其相对应的投影点Ai、Bi、Qi、Ci具有相同的交比Cr,即:
式中:AB、QB、AC、QC、AiBi、QiBi、AiCi、QiCi为2点之间的距离,点A、B、Q、C的物理世界坐标由棋盘格确定,Ai、Bi、Qi、Ci的图像坐标由角点提取算法从棋盘格图像中计算得到。由式(3)可计算出光平面上标定特征点Q在标定板平面坐标系下的局部世界坐标。如图 4所示,把标定板移动2次,可得到4个以上非共线特征点,并根据摄像机标定结果,可确定激光平面方程系数(a,b,c,d)。
3 激光中心线提取如图 5(a)所示,冰块(特别是明冰)对激光反射较弱、透射较强,导致大部分激光能量被吸收,难以得到高对比度激光线图像,给激光中心线提取带来极大困难。为此,本文提出粗、精2步定位法用于激光中心线提取。
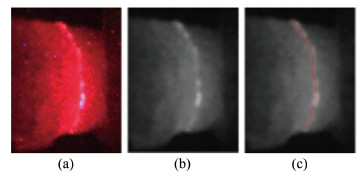 |
| 图 5 结冰表面激光线条图像及中心线提取结果 Fig 5 The center-line of laser line image on ice surface |
基本思路是:(1) 先对激光图像进行中值和高斯滤波,消除图像噪声干扰;(2) 结合R通道和灰度图像信息,对激光图像进行阈值分割,得到激光透射区域R;(3) 在分割区域R内,寻找每一行内最大像素作为粗定位结果;(4) 以粗定位结果为中心,在[-w,w]像素窗口内(本文取w=11),采用灰度重心法计算激光光条中心线亚像素位置,得到精定位结果。灰度重心法计算公式如下:
式中:u是像素横坐标,I是图像像素值。
图 5给出了冰块激光线中心线提取示例,其中图 5(b)是去噪后冰块灰度图像,图 5(c)是激光中心线提取结果。
4 实验结果及分析采用波长为650nm、线激光宽度可调的线激光器,以及分辨率为2048pixel×1536pixel的彩色摄像机,构成了如图 6所示简易冰形测量装置。在Matlab平台上编写了测量系统标定、激光中心线提取和激光光条三维坐标计算程序。
 |
| 图 6 放置于冰柜中的线结构光测量装置 Fig 6 The line structured light measurement device placed in a freezer |
在实验室环境下,采用形状已知的圆柱形冰块用于测量结果精度评估。圆柱形冰块半径为24mm。图 7(a)是拍摄的激光图像,图 7(b)是激光中心线提取结果。如图 8所示,以半径为24mm的圆弧作为真实值,与线结构光测量值进行对比。根据测量值拟合出的圆柱形冰块半径为23.991mm,圆柱形冰轮廓线测量值与真实值的均方根误差为0.536mm,平均相对误差为0.018,最大相对误差为0.052。
 |
| 图 7 圆形体冰块测量图像(a)及激光中心线提取结果(b) Fig 7 The captured laser line image (a) on cylindrical ice surface and the extracted center-line (b) of laser line image |
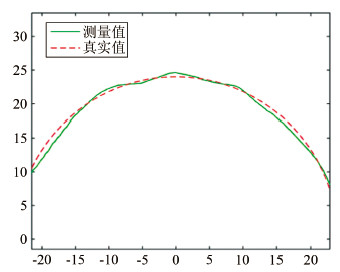 |
| 图 8 圆柱形冰轮廓线测量结果(单位:mm) Fig 8 The cylindrical ice cross sectional profile measurement result (unit: mm) |
此外,采用该测量装置对中国空气动力研究与发展中心的0.3m×0.2m结冰风洞进行了冰横截面轮廓测量。试验中采 用NACA0012翼型,迎角为2°,风速为35m/s,温度为-12℃,水压0.35MPa,气压0.30MPa,结冰时间2.5min。如图 6所示,在测量过程中为避免冰块融化,将冰块和测量装置放置于冰柜中,图 9给出了图 5所示冰横截面轮廓测量结果。
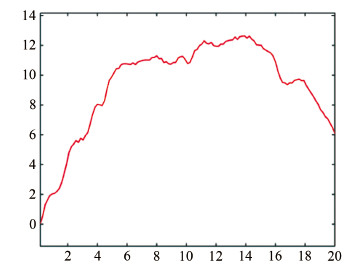 |
| 图 9 二元翼型结冰横截面轮廓测量结果(单位:mm) Fig 9 The cross section profile measurement results for the ice on a two elements airfoil (unit: mm) |
影响线结构光测量精度的主要因素包括2方面:测量系统标定精度和激光中心线提取精度。对于冰轮廓线测量而言,测量误差主要来源于激光中心线提取误差。影响激光中心线提取误差的根本原因为:冰块对激光线反射较弱,难以得到高对比度激光线图像。在本文的测量装置中,所使用的Bayer格式彩色摄像机无法充分感知冰块表面反射的激光线能量,此外镜头前端未使用滤波片导致背景区域杂散光进入摄像机降低了线激光图像对比度;此外,如图 6所示,为得到冰块横截面上的轮廓线,激光面垂直放置,而使摄像机未能与激光线反射方向对齐,导致摄像机所接受的激光线反射能量不足。这些因素共同导致了线激光图像对比度不高和图像信噪比差等问题。此外,该简易测量装置拍摄的冰块图像大小仅为200pixel×300pixel,未充分利用摄像机有效分辨率2048pixel×1536pixel,这意味着在冰块图像中1个像素表示的实际距离仅为1.33mm,影响冰块测量精度。
针对上述问题,需要改进测量装置光学系统:改用黑白摄像机,采用与线激光同波长的光学滤波片,以提高线激光图像能量、降低图像背景噪声;调整摄像机视野范围,使冰块完全覆盖成像区域,以提高成像像素利用率;使激光斜向投射在冰块表面,并在激光主反射方向上放置摄像机,以提高进入摄像机中的激光反射能量;采用转动棱镜或一维平移装置对冰块进行三维扫描测量,通过三维数据切片得到冰块横截面轮廓线。
5 结论为进行结冰生长过程冰形在线测量,本文初步探索了基于线结构光的冰轮廓线测量,设计了简易测量装置,编写了基于Matlab的测量系统标定、冰块透射表面激光中心线提取和激光光条三维坐标计算程序,进行了冰箱冻结冰块和结冰风洞冻结冰块轮廓线测量验证,证实了采用线结构光进行冰轮廓线测量的可行性。
下一步工作包括:首先,对各种冰(如明冰、霜冰、混合冰等)对激光线能量衰减问题进行针对性研究,从光学系统设计上进一步提升冰面激光线图像对比度,从图像处理算法上提升冰面激光中心线提取精度;其次,为进行结冰生长过程冰形在线三维测量,还需重点研究结冰试验条件下,如何消除冰粒、雾滴对摄像机成像的影响,以获得可靠的激光线图像;最后,研究如何在风洞试验状态下,利用转动棱镜或一维运动平台实现结冰过程中冰形三维扫描测量。
致谢: 感谢中国空气动力研究与发展中心易贤博士、杜艳霞博士、李伟斌博士、王梓旭、王茂等学者在风洞结冰试验与测试中提供的帮助和指导。
| [1] | 周莉, 徐浩军, 闵桂龙, 等. 结冰对飞机动态响应特性的影响[J]. 飞行力学, 2011, 29(4):32-36. Zhou L, Xu H J, Min G L. Effects of ice accretion on aircraft dynamic response[J]. Flight Dynamics, 2011, 29(4):32-36. |
| [2] | 钟长生, 杜亮, 洪冠新. 飞机结冰引起的飞行动力学问题探讨[J]. 飞行力学, 2004, 22(3):64-68. Zhong C S, Du L, Hong G X. The exploration of flight dynamics problem on aircraft icing[J]. Flight Dynamics, 2004, 22(3):64-68. |
| [3] | 易贤, 桂业伟, 朱国林, 等. 运输机翼型结冰的计算和实验[J]. 航空动力学报, 2011, 26(4):808-813. Yi X, Gui Y W, Zhu G L, et al. Experimental and computational investigation into ice accretion on airfoil of a transport aircraft[J]. Journal of Aerospace Power, 2011, 26(4):808-813. |
| [4] | 范洁川, 于涛. 飞机结冰风洞试验模拟研究[J]. 实验流体力学, 2007, 21(1):1-7. Fan J C, Yu T. A study of simulation for airplane icing tests in icing wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(1):1-7. |
| [5] | 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D].中国空气动力研究与发展中心, 2007. Yi X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang:China Aerodynamics Research and Development Center, 2007. |
| [6] | 杜雁霞, 桂业伟, 肖春华, 等. 飞机结冰过程的传热研究[J]. 工程热物理学报, 2009, 30(11):1923-1925. Du Y X, Gui Y W, Xiao C H. Investigation of heat transfer in aircraft icing[J]. Journal of Engineering Thermophysics, 2009, 30(11):1923-1925. |
| [7] | Ruff G A, Anderson D N. Quantification of ice accretions for icing scaling evaluations[R]. AIAA-98-0195, 1998. |
| [8] | 潘环, 艾剑良. 飞机结冰冰形预测的建模与仿真[J]. 系统仿真学报, 2014, 26(1):221-224. Pan H, Ai J L. Modeling and simulation of aircraft ice shape prediction[J]. Journal of System Simulation, 2014, 26(1):221-224. |
| [9] | Hovenac E A, Vargas M. A laser-based ice shape profilometer for use in icing wind tunnels[R]. NASA STI/Recon Technical Report N, 1995. 106936:1-7 |
| [10] | Zhang Long, Guo Longde, Yang Jianjun. Investigation of ice shape measurement technique based on laser sheet and machine vision in icing wind tunnel[C]. Image and Graphics, 2009. ICIG'09. Fifth International Conference on IEEE, 2009:790-795. |
| [11] | Gong Xiaoliang, Stephan Bansmer. Laser scanning applied for ice shape measurements[J]. Cold Regions Science and Technology, 2015, 115:64-76. |
| [12] | Gong Xiaoliang, Stephan Bansmer. 3-D ice shape measurements using mid-infrared laser scanning[J]. Optics Express, 2015, 23(4):4908-4926. |
| [13] | Abdel-Aziz Y I, Karara H M. Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry[J]. ASP Symposium on Close-Range Photogram, 1971, 81(2):103-107(5). |
| [14] | Tsai R Y. An efficient and accurate camera calibration technique for 3D machine vision[C]//Proceeding of IEEE Conference on Computer Vision & Pattern Recognition, 1986:364-374. |
| [15] | Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11):1330-1334. |
| [16] | Jean-Yves Bouguet. Camera Calibration Toolbox for Matlab[DB/OL]. http://www.vision.caltech.edu/bouguetj/calib_doc, 2015-10-14. |
| [17] | Moré J J. The Levenberg-Marquardt algorithm:implementation and theory//Numerical analysis[M]. Berlin:Springer Berlin Heidelberg, 1978:105-116. |
| [18] | Huyh D Q, Owens R A, Hartmann P E. Calibrating a structured light stripe system:a novel approach[J]. International Journal of Computer Vision, 1999, 33(1):73-86. |