对于大气层内飞行的飞行器的实时控制、导航和飞行后的数据分析,准确测量其飞行参数至关重要[1]。传统的测量系统采用基于压力测量的置于飞行器头部的空速管,以及安装在飞行器侧缘的迎角及侧滑角传感器等装置进行测量。但对于大迎角状态下飞行的飞行器,其前端及侧缘探出的传感装置会引起飞行器头部非对称涡流,从而导致较大的侧向力,导致飞行器横向不稳定。对于高超声速飞行状态,探出的传感装置会产生很大的热流,导致其难以正常工作。
针对上述问题,国外研发了嵌入式大气数据传感系统(Flush Air Data Sensing System,FADS)。国外对于FADS系统的研究起步较早,在20世纪60 年代,美国国家航空航天局(NASA)为了满足航天飞机进入大气层时的大气数据测量需要,提出了设计一种融于飞行器表面流线的大气数据传感系统的思想。FADS系统的基本思想是:大气数据通过一组非探出的配置在表面的测压孔测得的表面压力来计算出,并不需要探针深入周围的流场中来测量大气数据。这种方法可以避免头部的小曲率半径引起的高热流的影响,扩大了大气数据系统的应用范围,从亚、跨、超声速直至高超声速领域。FADS系统可以直接集成到飞行器的头部,不需要活动部件。由于FADS系统并不需要探测周围的流场,而是根据飞行器头部的压力分布来解算飞行参数,因此校准相对容易。由于FADS系统具有的优势,自20世纪60年代以来取得了巨大的发展。
60年代早期,FADS系统最初的原理模型在X-15飞行器中进行验证[2]。但是该系统机械设计繁琐,试验效果也不理想,在X-15飞行器项目结束后,这种在超声速状态下采用机械装置进行大气数据测量的思想便被抛弃。80年代初,Hillje和Nelson[3, 4]采用30°/10°组合锥体套接的大气数据传感系统(Ascent Air Data System,AADS)应用于航天飞机上升段中,并在低马赫数时对该系统进行了风洞试验校准,效果较好,但是该方法不适合于马赫数较高的情况。90年代初,FADS系统在F-14飞行器的跨声速、大迎角状态下进行过系统的测试,Terry等 [5]通过在机身头部不同周线上配置测压孔,利用压力传感器得到的数据对测压孔位置与飞行参数的敏感性进行了分析,对于如何选择有效的测压孔来计算飞行参数的计算方案进行了初步的探讨,以验证该系统在更宽泛飞行条件下的性能,并提供了全面详细的风洞测压数据。
近来,经过不断的发展及完善,FADS系统已被广泛试验应用于F-14、X-31、X-33、X-34、X-38和X-43等[5, 6, 7, 8, 9, 10, 11]各型飞行器上。针对用于钝头体上的FADS系统,目前国外技术已经比较成熟,而针对尖楔前体的FADS系统,其关键技术尚未突破。国内该项技术正在尝试实验中,从部分实验结果看,并不是非常理想[12]。 FADS系统的理论模型是建立在经典的空气动力学理论基础上的,因此必须要经过系统的风洞试验校准才能用于实际的飞行试验中。作为一项正在发展的新技术,目前国内未有公开的基于风洞实验校准用的实验数据。而校准是FADS系统实际应用中保证模型可靠性及精度不可缺少的一个环节。因此,本文基于国外文献中公开报道的F-14全面风洞实验测压数据,对于钝头机体用FADS系统进行了系统的校准,并对于相关的校准参数的变化趋势进行了详细的分析,以期为用于钝头体FADS系统的进一步发展提供参考。
1 FADS系统的大气数据测量原理 1.1 理论模型FADS系统的基本思想是通过测得的表面压力数据反推得到飞行参数,为此,需建立一个将表面压力与飞行参数关联起来的压力模型,该模型需适用较大的马赫数范围,并足够简单,通过简化的模型来描述复杂的流场问题。因此,FADS系统气动压力模型把势流模型(适用于亚声速条件)与修正的牛顿流模型(适用于超声速条件)[13],通过形压系数结合起来。形压系数综合考虑了气动外形、系统因素等影响,可以将其看作是马赫数、迎角及侧滑角的函数,飞行前可以通过风洞试验或CFD计算得到。
FADS系统的理论模型[1]为:
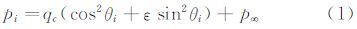
式中:pi为第i个测压孔测得的表面压力,qc为冲击动压,p∞为静压,ε为形压系数,其为马赫数、有效迎角及有效侧滑角的函数,
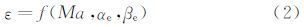
θi为第i个测压孔处的来流入射角(该点的法线方向与来流方向的夹角),由式(3)确定:
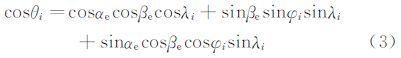
式中:αe,βe分别为有效迎角及侧滑角;φi,λi为第i个测压点的圆周角及圆锥角。测压点i的圆周角φi及圆锥角λi的定义如图 1所示。
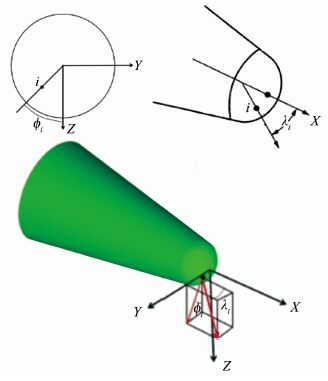
|
| 图 1 测压孔圆周角及圆锥角 Fig. 1 Sketch of clock and cone angle of the pressure port definitions |
针对钝头体,不同的测压孔选择方案对于迎角的精度影响较大,采用经典的三点式算法[1],可以建立迎角的求解方法。对于迎角三点式求解流程,具体为:
定义压差变量参数为
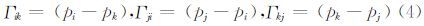
式中:pi,pj,pk为位于迎角平面的测压孔的压力值,其中3个测压点必须要包括驻点的压力。选取的其余2个测压点尽量与测压点1呈对称分布。通过三点法求解得到的迎角是有效迎角αe,并非真实迎角。
当|αe|≤45°时,取
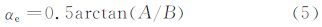
当|αe|>45°时,取
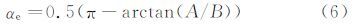
其中:
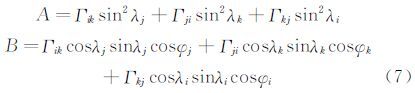
得到有效迎角后,取位于侧滑角平面上的测压点,其中驻点仍是必须包含的点,可以求解得到有效侧滑角:
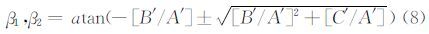
其中
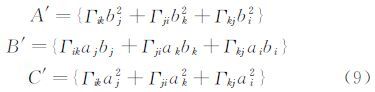
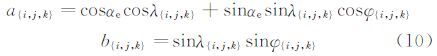
有效迎角及侧滑角的具体详细的选择方案,参见文献[1]。在得到有效迎角及侧滑角后,必须要进行校准,得到迎角修正量(上洗角)及侧滑角修正量(侧洗角)的校准曲线,进而得到真实迎角及侧滑角。
2 校准流程FADS系统经过风洞实验或数值计算校准,才能真正应用到实际飞行器中,本文采用风洞实验得到的测压数据进行校准,具体的校准方法为:
(1) 应用三点法,求解式(1),得到有效迎角ae及有效侧滑角βe;然后根据式(11)和(12)得出有效迎角及有效侧滑角的修正量δα和δβ,
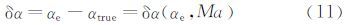
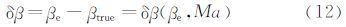
(2) 将αe和βe代入到式(3)中,得出各个压力测量点的入射角θi;
(3) 将式(2)中得到的入射角代入式(1),得到
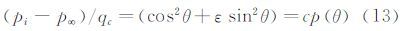
(4) 将式(13)改写为
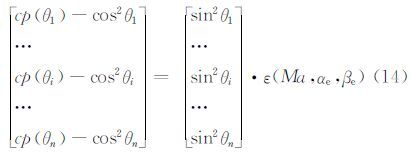
(5) 应用最小二乘法得到式(14)的一个最小二乘解,即为形压系数修正量
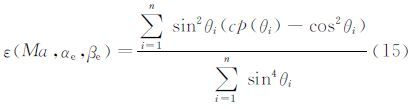
FADS系统的校准采用F-14飞行器外形,采用文献[5]提供的风洞实验数据,Ma=0.73、0.9、1.05、1.20、1.39;迎角范围α=-4°~20°;侧滑角范围β=-8°~8°。F-14飞行器上FADS系统的布点方案如图 2所示,具体位置信息如表 1所示。
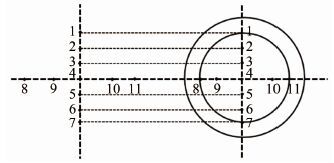
|
| 图 2 测压孔配置 Fig. 2 Pressure ports configuration |
| 测压点编号 | 圆周角φi/(°) | 圆锥角λi/(°) |
| 1 | 180 | 60 |
| 2 | 180 | 40 |
| 3 | 180 | 20 |
| 4 | 0 | 0 |
| 5 | 0 | 20 |
| 6 | 0 | 40 |
| 7 | 0 | 60 |
| 8 | 90 | 60 |
| 9 | 90 | 30 |
| 10 | 270 | 30 |
| 11 | 270 | 60 |
一般来说,迎角及侧滑角的校准是相互独立的,通过测得的一系列压力数据,分别得出校准关系数据,确定校准曲线。Ma=0.9时不同测压点组合得到的迎角偏差与有效迎角的关系如图 3所示。 不同的测压点组合得到的迎角修正量差别很大,有的已经背离实际情况。虽然通过校准后,偏差量可以修正,从而使得实际得到的迎角误差较小,但还是要选择最符合实际物理流动的测压点。王鹏等[14]对于测压孔的选取原则进行过较为详细的验证,本文不再详述。因此,实际选取的测压孔为(3,4,5),与王鹏等人的结论一致。
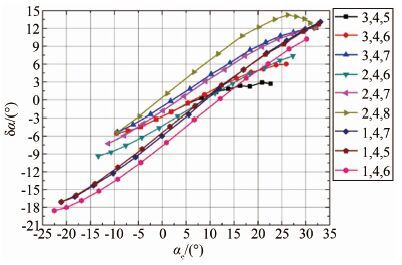
|
| 图 3 迎角参数的不同选点方案比较 Fig. 3 Variation of angle of attack parameters with effective angle-of-attack based on different pressure ports |
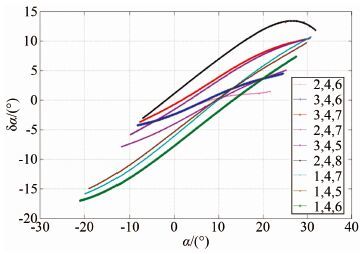
|
| 图 4 上洗角校准曲线 Fig. 4 Calibration curves for the angle-of-attack flow correction angle |
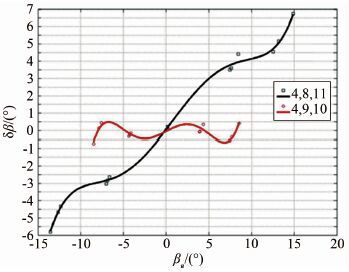
侧滑角的校准与迎角的校准相似。Ma=1.39时采用(4,8,11)及(4,9,10)测压点组合得到的迎角偏差量如图 5所示,采用(4,8,11)的偏差量太大,与实际不一致,因此侧滑角的测压点组合选取(4,9,11)。得到的校准曲线如图 6所示。
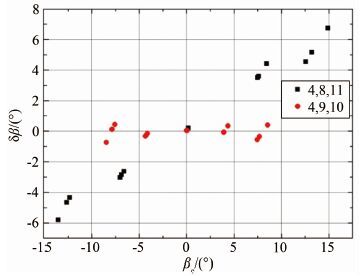
|
| 图 5 侧滑角参数的不同选点方案比较 Fig. 5 Variation of angle of sideslip parameters with effective angle of sideslip based on the different pressure ports |
|
| 图 6 侧洗角校准曲线 Fig. 6 Calibration curves for the angle-of-sideslip flow correction angle |
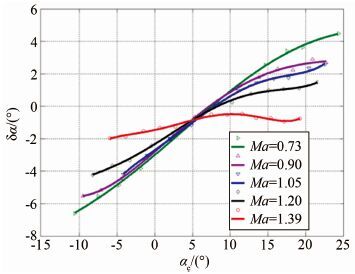
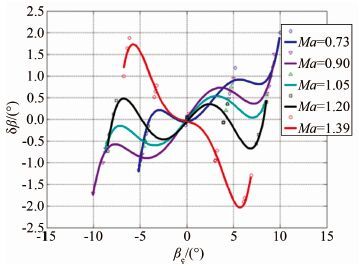
因此,对于迎角的校准,选取测压点(3,4,5),对于侧滑角的校准,选取测压点(4,9,11)。得到的在不同马赫数下的迎角及侧滑角修正量的校准曲线如图 7和8所示。
|
| 图 7 迎角校准曲线随马赫数的变化 Fig. 7 Calibration curves for angle-of-attack at Ma=0.73,0.90,1.05,1.20,1.39 |
|
| 图 8 侧滑角校准曲线随马赫数的变化 Fig. 8 Calibration curves for angle-of-sideslip at Ma=0.73,0.90,1.05,1.20,1.39 |
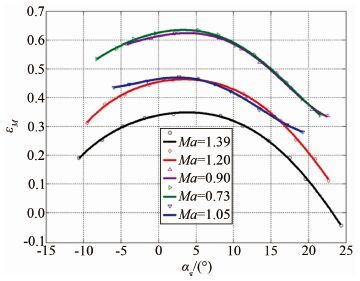
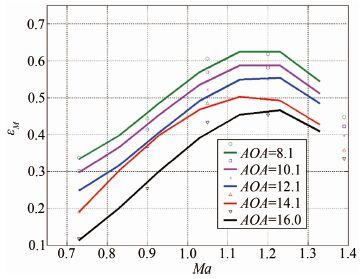
形压系数的校准方法按照第2节中的方法进行,得到的形压系数随有效迎角及马赫数的变化如图 9和10所示。
|
| 图 9 形压系数随迎角的变化 Fig. 9 Variation of the shape and compressibility parameter with effective angle-of-attack at Ma=0.73,0.90,1.05,1.20,1.39 |
|
| 图 10 形压系数随马赫数的变化 Fig. 10 Variation of the shape and compressibility parameter with Ma at α=8.1°,10.1°,12.1°,14.1°,16.0° |
在马赫数固定,侧滑角为0°时,形压系数随迎角的变化趋势为:F-14机头为非对称外形,形压系数的峰值不在0点,且随有效迎角的增大而减小;随Ma数的增加,形压系数趋近0;在迎角固定,侧滑角为0°时,形压系数随马赫数的变化趋势为:对于Ma<1.0,形压系数随Ma数增加而增加,形压系数在Ma=1.0附近变化较剧烈;此外,形压系数与风洞实验模型的尺寸相关。
4 结 论钝前体的FADS系统的气动模型是建立在势流理论及修正牛顿流理论基础上的,尽管已经比较成熟,但是仍需要进行风洞实验校准工作。飞行器机头表面的气流会受到机体诱导的侧洗和上洗的影响,改变了机头表面测压孔处气流的流向角。因此,通过模型得到的当地飞行数据,需要进行校正才能得到真实的大气数据。这就需要大批量的风洞实验校准,也就是说,FADS系统真正用于实际飞行之前,必须进行风洞实验校准。针对F14风洞测压实验数据,本文对钝头机体用FADS系统的3个关键参数进行了校准,得出的结论为:
(1)上洗角及侧洗角的校准与测压点的选取关系很大,不同的测压点可能会给出差别较大的预测结果,虽然理论上通过校准,多大的误差都可以修正,但是已经与实际不相符合,因此,合理选取测压点对于正确的校准至关重要。测压点中一定要包括驻点的测压点,其他2个测压点与驻点测压点呈对称分布。
(2)形压系数是难以校准的参数,形压系数反应的是整体的误差修正量,因为形压系数与飞行器的外形、马赫数、有效迎角及有效侧滑角相关。因此,对于形压系数的校准,需要综合考虑实际飞行器的外形及实验条件的影响。
| [1] | Cobleigh B R, Whitmore S A, Haering E A Jr, et al. Flush Air Data Sensing (FADS) system calibration procedures and results for blunt fore-bodies[R]. NASA TP-1999-209012, 1999. |
| [2] | John C P, Earl K R. Flight evaluation of the X-15 ball nose flow-direction sensor as an airdate system[R]. NASA TN D-2923, 1965. |
| [3] | Hillje E R, Nelson R L. Ascent air data system results from the space shuttle flight test program[R]. AIAA-80-0422, 1980. |
| [4] | Siemers P M, Wolf H. Shuttle entry air data system concepts applied to space shuttle orbiter flight pressure data to determine air data[R]. AIAA-83-0118, 1983. |
| [5] | Terry L J, Timothym R, Paul S M III. Wind-tunnel investigation of a flush air data system at Mach numbers from 0.7 to 1.4[R]. NASA TM-101697, 1990. |
| [6] | Whitmore S A, Mores T R, Larson T J. High angle-of-attack flush air data sensing system[J]. Journal of Aircraft, 1992,29(5): 915-919 |
| [7] | Whitmore S A, Cobleigh B R, Hearing E A. Design and calibration of the X-33 flush air data sensing(FADS)system[R]. NASATM-1998-206540,1998 |
| [8] | Westhelle C H. X-38 backup air data system[R]. AIAA-2002-0007, 2002. |
| [9] | Ellsworth J C, Whitmore S A. Reentry air data system for a sub-orbital spacecraft based on X-34 design[R]. AIAA-2007-1200, 2007. |
| [10] | Baumann E, Joseph W P. The X-43A flush air data sensing system flight test results[R]. AIAA-2008-6570, 2008. |
| [11] | Ellsworth J C. An analytical explanation for the X-43A flush air data sensing system pressure mismatch between flight and theory[R]. AIAA-2010-4964, 2010. |
| [12] | 秦永明, 张春. 嵌入式大气数据传感系统标定试验研究[C]//第九届全国实验流体力学学术会议论文集, 2013. Qin Y M, Zhang C. Experimental study of flush air data sensing system calibration[C]//The Ninth Chinese Conference of Experiments in Fluid Mechanics Papers, 2013. |
| [13] | Currie I G. Fundamental Mechanics of Fluids[M]. New York: McGraw-Hill, Inc, 1974. |
| [14] | 王鹏, 金鑫, 张卫民. FADS系统测压孔配置对迎角校准的影响[J]. 战术导弹技术, 2013, (2): 70-73. Wang P, Jin X, Zhang W M. Research on effect of configuration of pressure orifices on calibration for angle of attack[J]. Tactical Missile Technology, 2013, (2):51-55. |



