2. 北京立方天地科技有限责任公司, 北京 100083
2. MicroVec., Inc, Beijing 100083, China
湍流中的拟序结构被认为是湍流产生和发展的关键,因此针对拟序结构的研究一直是湍流研究的一个重要方向。近期的湍流研究主要关注拟序结构和湍流统计量之间的关系。Smits[1]在关于高雷诺数壁湍流的综述性文章中将拟序结构主要分为4类,包括近壁区条带,马蹄涡,大尺度结构(Large-Scale Motions,LSMs)和超大尺度结构(Very-Large-Scale Motions,VLSMs)。这里马蹄涡是对称以及不对称马蹄涡、Ω形涡和拱形涡的统称,这些涡一般由1个或2个流向涡腿和1个展向涡头组成,展向涡头的旋转方向和湍流边界层的平均剪切方向一致[2]。Adrian[3]用平面粒子图像测速(Particle Image Velocimetry,PIV)实验证明了在湍流边界层外区存在马蹄涡,同时这些马蹄涡的涡腿附着在壁面上并沿流向排列形成了流向涡包结构。目前,这种附着马蹄涡模型已被广泛接受[4]。但是,随着数值计算以及实验手段的不断改进和完善,有学者提出了不同的意见。Yang[5]通过马蹄涡发生器产生马蹄涡并观察马蹄涡向下游发展的情况,发现由涡产生的喷射(Ejection)现象能够导致二次马蹄涡的产生,并且能够诱导产生反向展向涡。Pirozzoli[6]通过条件平均进一步阐明了湍流中涡管和剪切层的相互作用,发现涡管基本分布在剪切层上并推断前者可能是Kelvin-Helmholtz不稳定性的产物。Lozano-Durán[7]在追踪拟序结构发展变化的过程中发现并不是所有的壁面附着结构都产生于壁面。Eitel-Amor[8]重做了Zhou[9]的数值实验,指出以前的研究[9, 10]可能过高地估计了马蹄涡存在的生命周期以及再生的重要性和鲁棒性,在湍流耗散环境中马蹄涡会很快衰减,不足以维持湍流大尺度运动。
通过上面的讨论可知,马蹄涡虽然能够成功地描述湍流边界层中的一些现象,但仍有学者对其在充分发展湍流中的重要性提出了疑问。在本文中,定义正展向涡和湍流边界层中马蹄涡头的方向一致,用“p”表示(Prograde Spanwise Vortices),负展向涡用“r”表示(Retrograde Spanwise Vortices),与湍流边界层平均剪切方向相反。众所周知,在湍流边界层中存在和马蹄涡涡头相反的负展向涡,而且总是和正展向涡成对出现[2, 6, 11]。随着雷诺数的升高,负展向涡的作用将变得更加明显[2]。目前,对负展向涡的产生机理主要有3种解释:正展向涡诱导局部剪切失稳[5],马蹄涡的相互合并[12]以及Ω形涡的一部分[11]。然而,由于旋涡结构复杂的三维特性,目前这些解释仍缺少三维流场的进一步实验验证。
想要完美地解释负展向涡的产生机理以及和正展向涡的关系,就必须得到时间解析的瞬时三维三分量(3D3C)速度场。随着科学技术的发展和实验手段的不断完善,层析PIV技术[13, 14]的出现使这种想法成为可能。从本质上讲,层析PIV和平面PIV的原理相同,它通过多相机多视角成像,然后利用倍增代数重构技术(Multiplicative Algebraic Reconstruction Technique,MART)得到流场示踪粒子的三维空间分布,进而互相关分析得到3D3C速度场。经过近10年的发展,层析PIV已经被用于测量高低雷诺数湍流边界层[15, 16]、零质量射流[17]、激波边界层相互作用[18]、三角翼前缘涡[19]以及涡环撞壁实验[20]等,得到了复杂流场的三维结构。
本文运用层析PIV技术测量了Reτ≈1700的湍流边界层,并且从统计角度对正负展向涡进行了分析,希望对湍流边界层中的拟序结构有更深入的理解。本文的组织结构如下:第1节和第2节分别介绍了层析PIV的具体实验方法以及旋涡辨识的方法,这2部分是数据分析的基础;第3节统计了正负展向涡沿法向的变化规律;第4节进一步讨论了正负展向涡的空间位置对流场速度的影响;第5节讨论了几个典型的三维流场结构;最后给出总结和结论。
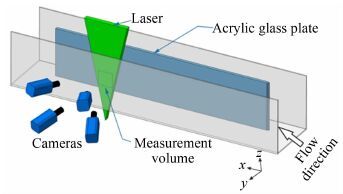
1 实验方法本实验在北京航空航天大学大水洞完成,整个测量工况如图 1所示,其中x,y,z分别代表流向、法向和展向。为了生成满足要求的湍流边界层,在大水洞中竖直安装了一块大小为7m×1m的有机玻璃板并且前缘为椭圆倒角,直径为3mm的拌线布置在距平板前缘0.1m的位置。水洞底壁的宽度为1m,玻璃板被安装在距侧壁0.6m的位置,实验时水位高度也为0.6m。测量体处在展向中心,距玻璃板前缘6.7m,下边界距平板壁面的高度为5.5mm。流场中投放平均粒径为20μm的空心玻璃微珠作为示踪粒子,其密度为1.05×10-3g·mm-3。4台分辨率为2456pixel×2048pixel的12位CCD相机呈“×”形布置在水洞一侧,相机之间的夹角约为60°,各台相机配置尼康f=45mm定焦体视镜头。为了减少由于视角引起的光学畸变,镜头的光圈f#被调到8和11之间,并且相机、镜头和物面满足Scheimpflug条件。光源采用500mJ双脉冲激光(镭宝光电Vlite-500 PIV专用双脉冲激光器),波长532nm,经过扩束光路被扩展成厚度为16mm的体光源。相机和激光之间通过同步器(北京立方天地SM-MicroPulse725同步器)进行控制,实验时激光频率为4Hz,2次曝光的时间间隔Δt=1.2ms。每台相机采样了300幅图像,采样时长约为38s,最终得到了150个速度场。
|
| 图 1 层析PIV实验工况示意图 Fig. 1 Experimental setup of Tomo-PIV in water tunnel |
层析PIV实验前需要标定物理空间和像素空间的关系。本文采用多项式标定(x,z方向采用三次多项式,y向采用一次多项式),标定板在测量体厚度范围内以2mm等间距移动并成像。初始得到的映射函数需要进行自修正[21],将映射函数的误差控制在0.1pixel以内,具体处理过程可以参考文献[22]。在层析PIV中,图像前处理也是一个非常重要的环节,可以很大程度上提升重构的精度和效率。本文对原始图像进行了时序最小背景剔除和空间滑动背景剔除,最终的图像进行了3×3的高斯平滑,高斯核σ=0.5。经过图像前处理后,粒子浓度约为0.06ppp(particle per pixel)。结合映射函数,空间粒子灰度场通过MART算法重构得到。本文进行10次MART迭代,重构体的大小为80mm×16mm×45mm,图像放大率为0.055mm/pixel,因此重构体素(voxel)的个数为1454voxel×290voxel×818voxel。
重构后的粒子灰度场直接通过互相关分析确定粒子的位移。本文采用多层迭代体变形算法[23],最终窗口大小为48voxel×48voxel×48voxel,重叠率为75%。为了提高计算效率,第1层互相关采用快速傅里叶变换算法(Fast Fourier Transform,FFT),其余互相关在得到速度参考矢量后进行窗口预偏置,然后采用小位移直接互相关算法。在体变形时只采用线性插值,这已经能满足计算精度的要求。另外,每一层互相关得到的速度场需要进行归一化坏点剔除[24]和高斯滤波,才能成为下一层互相关迭代的参考速度矢量。最终得到的速度场在剔除坏点的基础上进行了高斯平滑,平滑窗的大小为3×3×3,平滑强度σ=1。
流场的品质和参数通过激光多普勒测速(Laser Doppler Velocimetry,LDV)进行标定,表 1给出了流场的一些基本信息。实验时水温为18℃,对应的运动粘性系数ν为1.055mm2/s。当自由来流速度U∞约为0.413m/s时,流场的湍流度为0.97%。通过Musker方法[25]计算得到壁面摩阻速度uτ为15.57mm/s,边界层厚度δ为120mm,对应的基于壁面摩阻速度和动量厚度的雷诺数分别为1769和5176。根据公式用壁面粘性尺度(Wall Units,WU)对物理量进行无量纲化。
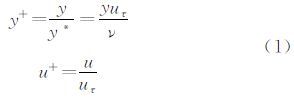
| ν/(mm2·s-1) | U∞/(mm·s-1) | uτ/(mm·s-1) | δ/mm | Reθ | Reτ |
| 1.055 | 412.8 | 15.57 | 119.8 | 5175.7 | 1768.7 |
因此,粘性尺度的测量体大小为1176WU×235WU×661WU。速度场的法向测量范围为100<y+<300(由于边界效应,实际分析的速度场法向范围略小于重构体的范围),流动位于对数区内。根据图像放大率计算出PIV互相关的判读体实际尺寸(即测量空间分辨率)为2.64mm×2.64mm×2.64mm≈38.8WU×38.8WU×38.8WU,速度矢量之间的间距(Δx+,Δy+,Δz+)为0.66mm≈9.7WU。最后,通过速度剖面(本文未给出)估计的测量误差没有超过0.1pixel,整体相对误差约为1.6%。
2 旋涡及涡心辨识方法 2.1 三维流场的旋涡辨识在湍流边界层中,存在涡量的地方可能存在旋涡,也可能是剪切层,因此,必须从湍流背景流场中提取真正的旋涡。根据Robinson[26]关于旋涡的定义,旋涡通常会以一定的速度对流,需要考虑伽利略不变性(Galilean Invariant),但在湍流边界层中旋涡的对流速度往往与所处位置的流动结构有关。目前的旋涡识别方法大多通过分析局部速度梯度张量来实现,例如Q准则、Δ准则、λ2准则以及λci准则,这些判据之间存在一定的联系,某些情况下是相互等价的[27]。本文采用基于当地脉动速度u的λci准则,即旋涡强度判据,该判据用局部速度梯度的复特征值的虚部来表示旋转的强度。由于分析的是脉动速度,湍流边界层当地时均速度U(仅考虑流向速度)已经从流场中剔除。考虑到PIV数据存在噪音以及空间分辨率的问题,速度梯度的计算往往存在误差。同时,旋涡强度在湍流边界层中并不是均匀分布,而是与法向高度y+有关。因此,阈值的设置不仅要考虑误差,还要考虑y+的影响。根据其他学者的研究成果[2, 11],本文阈值的设定如公式(2)所示。

式中:λcirms(y+)表示旋涡强度沿法向的标准差,通过全部样本统计得到。旋涡的方向通过归一化的实特征值对应的特征向量Λr=[Λx,Λy,Λz]来判断。结合涡量的正负,不同方向上的旋涡强度λci=[λcix,λciy,λciz]可表示为:
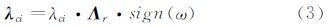
即,旋涡强度在旋涡方向上的投影。其中sign(ω)表示涡量的符号。为了进一步区分旋涡,若该旋涡的主轴方向与某个坐标轴的夹角小于30°(即分量大于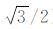 )就认为该旋涡在这个方向上占主导,这与Pirozzoli[6]所用的阈值(~26°)相似。没有特殊说明,流向、展向和法向涡都按此阈值定义。
)就认为该旋涡在这个方向上占主导,这与Pirozzoli[6]所用的阈值(~26°)相似。没有特殊说明,流向、展向和法向涡都按此阈值定义。
本文对展向涡的定位采用了类似文献[28]的方法,即找出展向涡所对应的连通区域,以该连通区域的质心作为三维流场中展向涡的位置。具体计算过程为:
(1)计算得到满足|Λz|>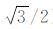 的连通域。为了排除噪音的干扰,连通域的大小至少为3个空间网格体;
的连通域。为了排除噪音的干扰,连通域的大小至少为3个空间网格体;
(2)计算每个连通域中λciz的质心,该质心的坐标用[xc,yc,zc]表示,该质心也是涡心的坐标;
(3)在[xc,yc,zc]处插值得到各个方向的旋涡强度[λcix,λciy,λciz]和对流速度[u,v,w];
(4)根据λciz的方向判断正展向涡和负展向涡。
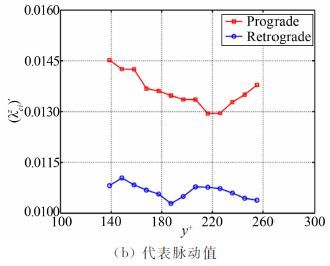
3 展向涡沿法向分布规律 3.1 展向涡强度 很多文献给出了涡量沿法向的变化规律,在对数区随着y+的增加而减小。图 2给出了正负展向涡强度沿法向的变化规律,曲线通过统计涡心处的展向涡强度得到,其中图 2(a)表示展向涡平均强度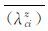 ,图 2(b)代表展向涡脉动强度(λciz)′。从图中可以看出:正展向涡(红色)的强度总体上沿法向减少,而负展向涡(蓝色)的强度几乎不变;同时,正展向涡的强度明显强于负展向涡。如果按同样的方法观察流向和法向涡沿y+的变化规律,正负涡强度几乎没有差别,都随着y+的增加而降低。也就是说,对于不同方向的旋涡,只有正负展向涡的强度存在较大的差别,这一事实进一步证明了湍流的各向异性。在图 2中y+=220的位置处出现了一个拐点,正展向涡的强度有增加的趋势,出现这一现象的原因有2点:一是本文考虑了展向涡的方向,与其他学者统计的方法不同;二是由于本文的样本数较少,可能还没有达到统计收敛。
,图 2(b)代表展向涡脉动强度(λciz)′。从图中可以看出:正展向涡(红色)的强度总体上沿法向减少,而负展向涡(蓝色)的强度几乎不变;同时,正展向涡的强度明显强于负展向涡。如果按同样的方法观察流向和法向涡沿y+的变化规律,正负涡强度几乎没有差别,都随着y+的增加而降低。也就是说,对于不同方向的旋涡,只有正负展向涡的强度存在较大的差别,这一事实进一步证明了湍流的各向异性。在图 2中y+=220的位置处出现了一个拐点,正展向涡的强度有增加的趋势,出现这一现象的原因有2点:一是本文考虑了展向涡的方向,与其他学者统计的方法不同;二是由于本文的样本数较少,可能还没有达到统计收敛。
|
| 图 2 正负展向涡强度沿法向变化规律 Fig. 2 The strength of spanwise vortices along the wall-normal direction |
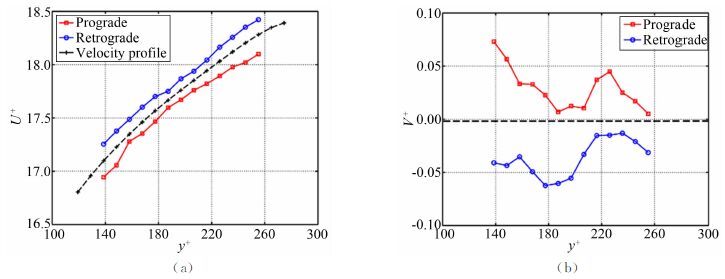
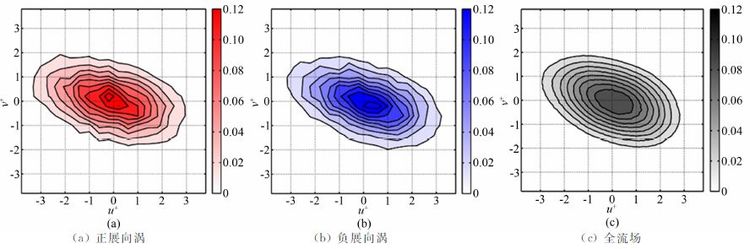
在第2节中已经给出了涡心坐标的计算方法,即计算质心坐标,进一步插值得到各个涡心的速度,该速度虽然是欧拉坐标下的速度,但根据旋涡的定义可以用来代表旋涡的对流速度。图 3给出了测量高度内展向涡的流向平均对流速度(见图 3(a))和法向平均对流速度(见图 3(b))。整体上,负展向涡的流向对流速度高于平均速度而正展向涡的速度低于平均速度。从图 3(b)可以看出,正展向涡的平均法向速度大于0,即向上运动,而负展向涡的平均法向速度小于0,朝下运动。由于样本数较少,曲线不是很光滑,但趋势还是非常明显。为了进一步明确涡心对流速度的分布,图 4给出了不区分高度的u,v联合概率密度分布,其中图 4(a)代表正展向涡,图 4(b)代表负展向涡,图 4(c)表示全流场所有空间点上的速度。统计上流向速度与法向速度之间存在相关性:当流向速度大于当地平均速度时法向速度朝下且速度增大,类似湍流中的扫掠(sweep,u>0,v<0)现象;当流向速度小于当地平均时法向速度朝上,类似喷射(ejection,u<0,v>0)。另外,对于正负展向涡,对流速度概率最高的位置分别出现在第二、四象限。大部分正展向涡朝上运动,但是也有相当一部分朝下运动,这一点和附着涡模型[3, 4]不太一致。如果从雷诺应力-uv大于0的角度出发,高低速区域与雷诺应力有很好的相关性,贡献了大部分雷诺应力,并且流场中发生扫掠和喷射的概率很高。
|
| 图 3 正负展向涡的流向对流速度(a)和法向对流速度(b)沿高度的变化。(a)中的黑色虚线代表速度剖面,(b)中的黑色虚线代表V+=0。 Fig. 3 (a) The mean streamwise velocity of prograde and retrograde spanwise vortices as a function of y+,the black dotted line represents the mean velocity profile. (b) The mean wall-normal velocity of prograde and retrograde spanwise vortices as a function of y+,the black dotted line represents V+=0. |
|
| 图 4 流向速度和法向速度的联合概率密度分布 Fig. 4 The joint probability density function of streamwise velocity and wall-normal velocity. (a) prograde spanwise vortices,(b) retrograde spanwise vortices,(c) the whole flow field. |
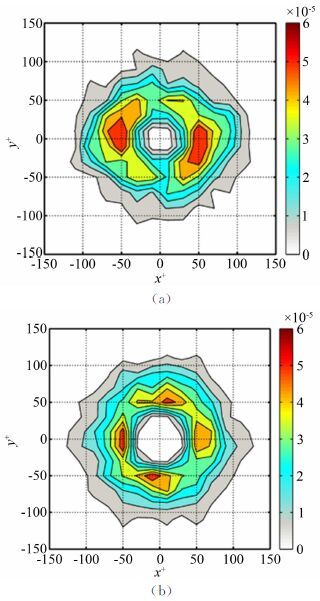
通过第3节的分析可知:正负展向涡在法向的区别主要集中在强度、空间流场结构以及对流速度上,本节主要讨论正负展向涡在x-y平面内的空间关系。以正展向涡的涡心为中心,在半径为200WU的区域内统计周围正负展向涡出现的概率,在展向z允许有±2Δz+(±19.4WU)的偏差。在统计过程中,同一个展向涡如果同时被不同的中心涡选中,则选择其中距离最近的一个。图 5为统计得到的结果,图 5(a)表示中心为正展向涡时周围正展向涡的分布情况,而图 5(b)表示中心是正展向涡,负展向涡在其周围的分布情况,横纵坐标分别表示离中心涡的流向和法向距离,云图代表周围涡出现的概率,颜色越红说明在该位置出现的概率越高。在图 5中,正展向涡基本上沿流向水平排列,间距约为60WU,由于样本数量有限导致统计的分辨率较低。对于图 5(b)中的负展向涡,基本上分布在正展向涡的流向和法向。Natrajan[11]在文章中展示了法向分布的这种情况,但并没有展示流向分布这种情况,在实际流场中,后者往往也是存在的,其出现的概率几乎和法向出现的概率相等。另外,仔细观察负展向涡法向出现的位置可以发现:在正展向涡底部时其偏向上流,而在正展向涡上部时偏向下游,这与Natrajan[11]的结果一致。
|
| 图 5 正展向涡(a)和负展向涡(b)在正展向涡周围的分布情况 Fig. 5 The distribution of prograde (a) and retrograde (b) spanwise vortices around a prograde vortex |
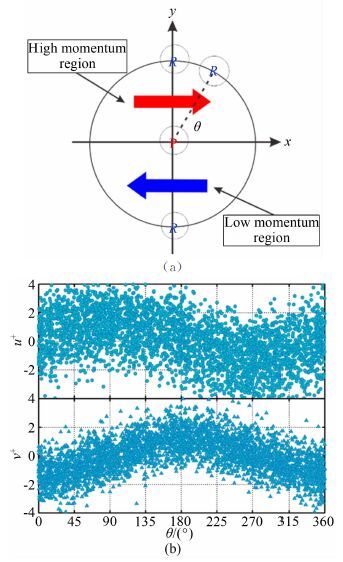
进一步分析正负展向涡的空间位置对流场速度的影响。如图 6(a)所示,以正展向涡为中心,负展向涡的位置可以用他们之间的连线与流向的夹角θ表示(半径变化较小,一般在100个粘性尺度以内,如图 5(b)所示)。θ的取值范围为0°到360°,180°和0°表示负展向涡在正展向涡的上下游,而90°和270°表示在上层和下层。连线中心的脉动速度可以由插值得出,用该速度可以比较容易和准确地判断出流场速度与展向涡空间位置的关系。图 6(b)给出了连线中心的脉动速度(u+,v+)随角度θ的变化规律,圆点代表流向速度u+,三角代表法向速度v+。随着角度的变化,流向速度呈现出正弦曲线的变化规律,而法向速度表现出与之相对的余弦变化趋势。当负展向涡分布在正展向涡的流向,即θ为0°或180°时,流向速度的平均值几乎为0,而法向速度的平均值却最大,约为1.2;当负展向涡分布在正展向涡的法向时,即θ为90°或270°时,流向速度表现出高低速区域,而法向速度却维持在0左右,如图 6(a)中的红蓝箭头所示。该规律完全背离了图 4所描述的速度之间的依赖关系,高低速区的产生无法简单地用扫掠和喷射来解释。需要注意的是,这种和涡结构有很强关系的高低速区域的尺度都比较小,与图 5中展向涡之间的距离相当。一般来说,喷射产生于近壁区并逐渐向上运动,相反,扫掠产生于较高位置朝壁面运动[7]。这种大范围相对运动容易产生大尺度结构,而中小尺度的流动结构更多是由于不稳定性和旋涡运动造成的。
|
| 图 6 (a)高低速区域与正负展向涡位置关系示意图,(b)速度与正负展向涡空间位置的关系 Fig. 6 (a) The schematic diagram about the relationship between the low (high) momentum region and the spatial arrangement of spanwise vortices,(b) The corresponding variations in u+(v+) and θ |
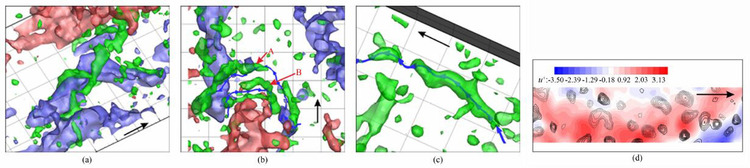
目前,尽管层析PIV的分辨率和精度还有待进一步提高,但它在获取三维大尺度流动结构上已表现出了一定的优势。本节将主要展示通过层析PIV获得的三维流动结构,如图 7所示。图 7(a)、(b)和(c)中的绿色等值面代表旋涡强度λci/λcirms(y+)=3.8,图 7(a)和(b)中的蓝色和红色等值面分别代表低速区和高速区。图 7(b)和(c)中的蓝色实线为涡线,箭头指示旋涡方向。图 7(d)为某一瞬时x-y截面的流向速度u+的云图,黑色实等值线为正展向涡,虚等值线为负展向涡。图 7(a)给出了一种较常见的情况,即一个低速条带被环形涡裹挟,条带的摆动和涡的方向耦合在一起。图 7(b)所示的情况较为复杂,在一个较大的拱形涡(红色A所指)上游有一个较小的反向拱形涡(红色B所指),旋涡方向可以通过蓝色涡线判断。Adrian[12]认为这是由于2个对称的Ω形的涡在展向合并造成的。从图 7(c)中穿过涡量等值面中心的涡线可以看出:该等值面表示一个流向涡,在该流向涡的下游并没有出现很强的展向涡,而是类似螺旋的结构。图 7(d)所展示的平面流动结构中,高速区域(红色)的上方是负展向涡,下方是正展向涡,也就是说高速区域的形成可能和涡结构的空间位置有关。通过上面的观察,在充分发展湍流边界层的局部小尺度区域内流动结构更多地和局部不稳定性以及涡的相互作用有关,表现出复杂性和多样性。因此,旋涡结构和高低速区域之间的关系需要进一步深入系统地研究。
|
| 图 7 湍流边界层中的流动结构。(a)蓝色和红色等值面分别代表u+=-2.1和2.3,绿色是旋涡强度等值面λci/λcirms(y+)=3.8。(b)同(a),蓝色实线为涡线,箭头指示旋涡方向,红色A,B分别指示较大和较小的拱形涡,两涡的方向相反。(c)绿色等值面代表λci/λcirms(y+)=3.8,蓝色涡线从等值面中心穿过。(d)某一瞬时x-y截面的流向速度u+的云图,红色表示高速区域,蓝色表示低速区域,虚线表示负展向涡,实线表示正展向涡。黑色箭头表示流动方向 Fig. 7 The three dimensional plots of instantaneous flow structures in TBL. (a) the blue and red volume represent the iso-surface of u+=-2.1 and 2.3 respectively,the green is the iso-surface of swirl λci/λcirms(y+)=3.8. (b) the same with (a),the blue solid line represents the direction of vortices,the red A and B indicate two opposite vortexes,A is larger at downstream and B is smaller at upstream. (c) the same with (b). (d) The instantaneous contour of u+ in the plane of x-y. The red represents high momentum region,and the blue represents low momentum region. The solid and dotted black line represent prograde and retrograde spanwise vortices respectively. The black arrow in all the panels represents the flow direction |
本文通过层析PIV测量了Reτ≈1700的湍流边界层,并统计分析了100<y+<300内边界层中展向涡的规律。结果表明:
(1) 对于旋涡强度,正负展向涡表现出不同的性质。随着法向高度的增加正展向涡逐渐变弱而负展向涡基本保持不变。
(2) 流向速度和法向速度呈现出很强的相关性,导致流场中的大尺度高低速区域成为雷诺应力-uv的主要来源。
(3) 正展向涡在流向呈现出等间距分布,而负展向涡大多分布在正展向涡的流向和法向,但并没有统计这种分布在流向持续的长度。
(4) 在小尺度范围内(约为100WU),高低速区域并不受喷射和扫掠机制的控制,而是更多和涡结构的空间位置以及局部不稳定性有关。
| [1] | Smits A J, Mckeon B J, Marusic I. High-Reynolds number wall turbulence[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 353-375. |
| [2] | Wu Y, Christensen K T. Population trends of spanwise vortices in wall turbulence[J]. J Fluid Mech, 2006, 568: 55-76. |
| [3] | Adrian R J, Meinhart C D, Tomkins C D. Vortex organization in the outer region of the turbulent boundary layer[J]. J Fluid Mech, 2000, 422: 1-54. |
| [4] | Adrian R J. Hairpin vortex organization in wall turbulence[J]. Physics of Fluids, 2007, 19(4). |
| [5] | Yang W, Meng H, Sheng J. Dynamics of hairpin vortices generated by a mixing tab in a channel flow[J]. Exp Fluids, 2001, 30(6): 705-722. |
| [6] | Pirozzoli S. Flow organization near shear layers in turbulent wall-bounded flows[J]. Journal of Turbulence, 2011: N41. |
| [7] | Lozano-Durán A, Jiménez J. Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades[J]. J Fluid Mech, 2014, 759: 432-471. |
| [8] | Eitel-Amor G, Örlü R, Schlatter P, et al. Hairpin vortices in turbulent boundary layers[J]. Physics of Fluids, 2015, 27(2): 025108. |
| [9] | Zhou J, Adrian R J, Balachandar S, et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. J Fluid Mech, 1999, 387: 353-396. |
| [10] | Kim K, Sung H J, Adrian R J. Effects of background noise on generating coherent packets of hairpin vortices[J]. Physics of Fluids, 2008, 20(10): 105107. |
| [11] | Natrajan V K, Wu Y, Christensen K T. Spatial signatures of retrograde spanwise vortices in wall turbulence[J]. J Fluid Mech, 2007, 574: 155-167. |
| [12] | Adrian R J, Balachandar S, Lin Z C. Spanwise growth of vortex structure in wall turbulence[J]. KSME International Journal, 2001, 15(12): 1741-1749. |
| [13] | Gao Q, Wang H P, Shen G X. Review on development of volumetric particle image velocimetry[J]. Chinese Science Bulletin, 2013, 58(36): 4541-4556. |
| [14] | Elsinga G E, Scarano F, Wieneke B, et al. Tomographic particle image velocimetry[J]. Exp Fluids, 2006, 41(6): 933-947. |
| [15] | Elsinga G E, Adrian R J, Van Oudheusden B W, et al. Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer[J]. J Fluid Mech, 2010, 644: 35-60. |
| [16] | Gao Q. Evolution of eddies and packets in turbulent boundary layers[D]. Minnesota: The University of Minnesota, 2011. |
| [17] | 高琪, 王洪平. 层析PIV技术及其合成射流测量[J]. 中国科学:技术科学, 2013, (7): 828-835. Gao Q, Wang H P. The tomographic PIV and it's application on synthetic jet measurement[J]. Science China: Technological Sciences, 2013, (7): 828-835. |
| [18] | Humble R A, Elsinga G E, Scarano F, et al. Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction[J]. J Fluid Mech, 2009, 622: 33-62. |
| [19] | 王成跃, 高琪, 魏润杰, 等. 三角翼前缘涡三维流动显示和层析PIV测量[C]. 第八届全国流体力学学术会议, 2014. Wang C Y, Gao Q, Wei R J, et al. 3D flow visualization and tomographic particle image [JP]velocimetry for vortex breakdown of a delta wing[C]. The 8th National Congress of Fluid Mechanics, 2014. |
| [20] | Violato D, Ianiro A, Cardone G, et al. Investigation on circular and chevron impinging jets by IR thermography and time-resolved tomographic PIV[C]. ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, 2011. |
| [21] | Wieneke B. Volume self-calibration for 3D particle image velocimetry[J]. Exp Fluids, 2008, 45(4): 549-556. |
| [22] | Gao Q, Wang H P, Wang J J. A single camera volumetric particle image velocimetry and its application[J]. Science China: Technological Sciences, 2012, 55(9): 2501-2510. |
| [23] | Scarano F. Iterative image deformation methods in PIV[J]. Meas Sci Technol, 2002, 13(1): R1-R19.[LL] |
| [24] | Westerweel J, Scarano F. Universal outlier detection for PIV data[J]. Exp Fluids, 2005, 39(6): 1096-1100. |
| [25] | Kendall A, Koochesfahani M. A method for estimating wall friction in turbulent wall-bounded flows[J]. Exp Fluids, 2008, 44(5): 773-780. |
| [26] | Robinson S K. Coherent motions in the turbulent boundary layer[J]. Annual Review of Fluid Mechanics, 1991, 23(1): 601-639. |
| [27] | Chakraborty P, Balachandar S, Adrian R J. On the relationships between local vortex identification schemes[J]. J Fluid Mech, 2005, 535: 189-214. |
| [28] | Del Alamo J C, Jiménez J, Zandonade P, et al. Self-similar vortex clusters in the turbulent logarithmic region[J]. J Fluid Mech, 2006, 561: 329-358. |



