2. 东北农业大学理学院, 哈尔滨 150030;
3. 日本鸟取大学 地域学部, 鸟取 6808551
2. College of Science, Northeast Agricultural University, Harbin 150030, China;
3. Regional Faulty, Tottori University, Tottori 6808551, Japan
近年来,由于极寒天气的频繁出现使得风力机叶片结冰问题逐渐受到了广泛关注[1, 2, 3, 4, 5]。研究叶片的结冰机理和防除冰技术的主要手段之一就是利用结冰风洞来实际测试。结冰风洞是一种模拟在寒冷环境中过冷水滴在一定风速带动下撞击到物体表面结冰的实验设备。结冰风洞多用于航天航空领域,最主要的就是机翼结冰,还有发动机、传感器及相关零部件结冰。目前世界上能够进行结冰实验的风洞有20余座,主要分布在美国、加拿大、法国、英国、意大利和俄罗斯等国家。其中具有代表性的是美国NASA 刘易斯研究中心的闭式结冰风洞,意大利的IWI结冰风洞及中国空气动力研究与发展中心于2014年完成的3m×2m 大型冰风洞[6, 7, 8]。然而,这些风洞规模大、耗能多、成本高,中、小科研院所和高校很难建设和使用。因此,研制结构简单,能耗低廉的结冰风洞成为结冰研究的一个重要方向。风力机工作的环境就是在地表,属于在自然环境下的结冰问题,而不是像飞机属于高空特殊环境下的结冰。因此,研究风力机叶片结冰问题,在某种意义上来说并不需要如此高精度、高成本的结冰风洞,接近自然条件的低温环境风洞更适合。另外,如果利用自然低温为结冰风洞提供冷源的话,既省去了复杂的人工制冷设备,降低设备成本费用,又省去了人工制冷设备的能耗,降低设备使用费用。通过自然低温为冰风洞制冷在国际上已有先例,加拿大在1942年就建造了一座开式的简易冰风洞,利用冬季寒冷的气候自然制冷;位于明尼苏达州首府的Fluidyne Engineering Corp利用冬季寒冷环境为冰风洞制冷,所研发的开环式冰风洞主要用于发动机防冰研究[9]。在国内还没有利用自然低温进行制冷的冰风洞。
综上所述,为了研究风力机的结冰特性与开发防除冰系统,本研究利用东北地区特有的低温环境,在常规开口射流式风洞的基础上,安装水雾喷射系统并增加实验气道,提供结冰环境条件,设计了利用自然低温的风力机结冰风洞实验系统。该实验系统利用自然低温可省去人工制冷设备,大幅降低安装使用的成本及能耗,实现较长时间的结冰测试。在2015年冬季,对结冰风洞的主要参数进行了测试和标定,包括温度稳定性、液态水含量和过冷水滴平均直径,验证了该系统的有效性。
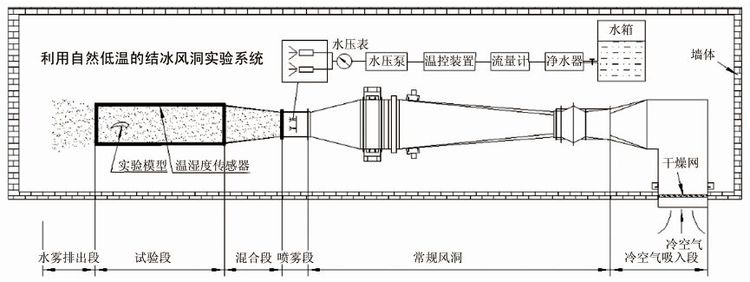
1 结冰风洞设计图 1为设计的利用自然低温风力机结冰风洞实验系统。所用的基础风洞为日本鸟取大学工学部设计制造的开口射流式风洞,实验段截面为0.6m×0.6m,风速范围为1~15m/s。在该风洞的原吹出口处安装了水雾喷射系统,在其后设置了喷雾段、混合段和实验段。室外冷空气由冷风段吸入后,喷雾系统喷出的过冷水滴在混合段充分混合,然后作用于实验段的实验物上结冰。其中喷雾系统包括喷头,水压表,水压泵,温控装置,流量计及净水器。通过调整风速、喷头数量、喷嘴口径及水压组合来控制水滴的流量及水滴粒径。图 2为利用自然低温的结冰风洞实验系统实物图。
|
| 图 1 结冰风洞实验系统简图 Fig. 1 Sketch of icing wind tunnel test system |

|
| 图 2 结冰风洞实验系统 Fig. 2 Icing wind tunnel test system |
温度是影响结冰的重要参数,直接影响到结冰的类型和外形。冰风洞能否提供稳定的过冷环境成为验证其有效性的重要指标。在本研究中利用自然低温进行实验,无法对温度进行精确调节,但实验可选择在相近的环境温度下进行,可保持实验段内过冷温度稳定。
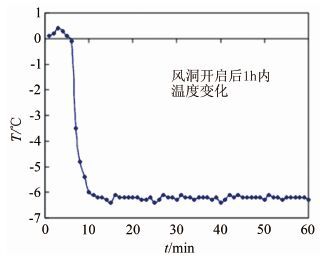
图 3所示列举了某一时间段内风洞开启1h实验段温度的变化情况。实验中采用HTC-1温度传感器实时测量风洞实验段温度,温度传感器测量范围为-50~70℃,测量精度为±0.5℃。可以发现风洞从开始降温直至达到稳定,并在-6.2℃范围内保持较长时间,温度误差不超过0.5℃。在实验过程中,先对实验段进行降温,当达到温度稳定后,开启喷雾系统进行结冰实验并实时记录环境温度,使实验过程始终在相对稳定的低温环境中进行。因此,只要在外界环境温度相对稳定的时间段内进行实验,结冰风洞实验段的温度便可保持非常好的稳定性,满足结冰风洞的实验要求。
|
| 图 3 试验段温度变化举例 Fig. 3 Example of temperature change in wind tunnel |
液态水含量(Liquid Water Content,LWC,g/m3)是指单位体积的空气中所含有的液态水质量。LWC是影响结冰形状和结冰类型的重要结冰云雾参数,得到结冰风洞中LWC分布,是得到定量结冰风洞实验结果的基础。对于结冰风洞中LWC的测量,有直接法和间接法2种。本研究采用的是间接法,即将由冰刀法衍生而成的栅格置于实验段中进行实验,通过分析栅格上的结冰质量推算出LWC。
2.2.1 液态水含量计算方法[10]结冰是由于过冷水滴碰撞到物面而导致的,在物体外形和空气绕流条件一定的情况下,水滴的运动轨迹只和水滴的粒径有关系。在所有运动轨迹中,物体上下表面最远撞击点所对应的轨迹为极限轨迹。位于极限轨迹之间的水滴会与物面碰撞,而在极限轨迹之外的水滴将绕过物体。记水滴的收集系数为Em,对于单位宽度d的栅格棱而言,远场中两条极限轨迹之间的距离为Δy,则有

假设来流速度为v,在极限轨迹间的水滴在单位时间内和单位宽度上的结冰质量Mi,则有
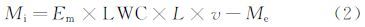
式中:Me为单位时间物体表面蒸发量;v为来流速度;L为单位展长。
由于栅格棱的宽度较小,故在标定规程中取Δy=d,即Em=1,同时忽略表面蒸发量,即Me=0,则式(2)可以变换为
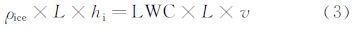
式中:ρice为冰的密度(实验过程中实时测量);hi为栅格棱上结冰厚度。
整理得任意栅格棱条处的LWC为
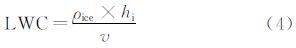
图 4所示为进行标定过程中所用的栅格,其整体尺寸为568mm×568mm,栅格的横、纵棱的中心间距为80mm,横、纵棱的宽度为8mm。在结冰实验条件下,将栅格放入实验段中进行结冰实验,获得一定时间的结冰栅格棱上的结冰厚度,根据位于极限轨迹之间的水滴与物面碰撞结冰原理,计算出实验段的液态水分布情况。为减小实验误差,对同种工况下栅格结冰进行4次实验,取4次实验的均值为风洞的LWC值。

|
| 图 4 结冰厚度测试用栅格 Fig. 4 Mesh for icing thickness measurement |
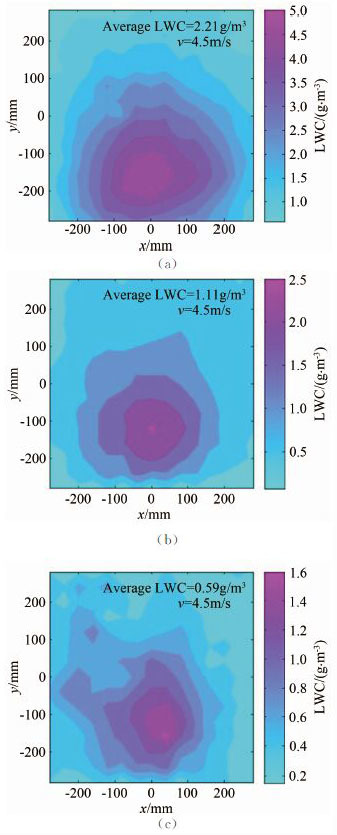
图 5所示给出了风速为4.5m/s下的3种液态水分布云图。通过云图可以发现,在冰风洞实验段的中心部分产生了150mm×150mm的均匀区域,在该范围内可进行静态叶片的结冰实验研究。同时,围绕中心形成多个液态水含量相近的环形区域,在该区域内可进行风力机叶片段的旋转结冰实验。
|
| 图 5 实验段液态水分布 Fig. 5 The distribution of LWC in the experimental section |
过冷水滴粒径(Medium Volume Diameter,MVD)大小是重要的结冰云雾参数,获得结冰风洞内水滴粒径,是得到定量结冰风洞实验结果的基础。对于实验段中运动的过冷水滴,常通过多普勒粒子分析、光学阵列探测等方法,所使用设备及方法复杂且昂贵。
在本研究中采用数值计算与风洞实验相结合的手段标定水滴直径。其分析思路如下,测量ΔT结冰时间内,速度为v对应任意碰撞物面位置sn处的结冰厚度为hn,在此基础上hn的表达式可以写为
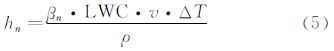
式中:βn为任意碰撞物面位置sn处的水滴收集率。在物体外形和空气流动一定情况下,任意碰撞物面的sn处的水滴收集率只和水滴直径有关。定义水滴撞击的起始位置s0,sn表示碰撞点距离起始位置s0的物面曲面距离,此处的局部收集系数βn满足
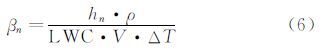
针对上述特性对冰风洞水滴粒子直径标定方法如下:选取典型外形(圆柱)进行风洞实验,测得多个碰撞物面sn处的结冰厚度hn,得到局部撞击极限βn与碰撞物面sn的关系曲线βn0=β(sn);针对冰风洞实验的空气绕流条件,通过数值计算的方法获得不同粒径所对应的局部撞击极限βn与碰撞物面sn的关系曲线βnm=β(sn);将实验测量的关系曲线βn0=β(sn)与多条关系曲线βnm=β(sn)进行比对,最终得出水滴粒径分布情况。
2.3.2 局部收集系数计算方法[11]通过数值计算的方法求解水滴粒子运动轨迹及撞击极限,先要计算空气的流场,在得到流场分布基础后分析单个水滴的运动轨迹及其撞击特性,再求解多个粒子的轨迹簇,进而确定水滴的撞击极限,最后分析任意碰撞物面位置sn处的水滴收集率。
控制方程为低速粘流的时均N-S方程,取其通用形式为
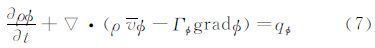
采用标准的κ-ε湍流模型,采用Simple方法求解方程(7),方程(7)各项的物理意义及具体表达式可参见文献[12]。
在流场解算的基础上建立水滴的运动方程,首先做如下假设:(1)水滴的体积保持不变;(2)水滴密度在整个过程中保持不变;(3)水滴的初始速度与自由流的速度相等,水滴质量较小不影响流场性质,通过分析运动中水滴的受力、根据牛顿第二运动定律建立水滴的运动方程为
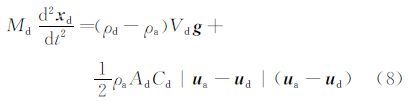
式中:xd代表水滴位置,Md为水滴质量,Vd为水滴体积,ρd为水滴密度,ρa是空气密度,g是重力加速度,Ad是水滴的迎风面积,Vd是水滴的体积,Cd是阻力系数,ua代表当地气流速度,ud代表水滴速度。
采用Euler方法离散求解水滴运动方程,其在x轴方向的方程加速度方程为
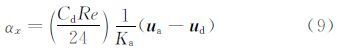
y轴方向水滴的加速度方程为
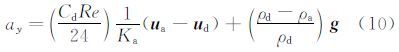
由水滴的加速度得出在tn时刻水滴的速度为(udn,vdn),所处的位置为(xdn,ydn),则在tn+1时刻水滴速度和位置为
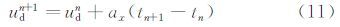
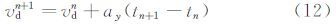
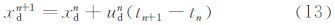
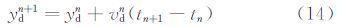
开始计算时给定水滴的初始位置,然后计算Δt时间步长后水滴的新位置。水滴在物面的最远撞击点所对应的轨迹为极限轨迹,极限轨迹分别于物体的表面两侧相切。
通过水滴轨迹计算确定撞击点位置之后,就能够获得一组水滴纵向点出发点位置(y0,y1,y2,…,yn)以及其对已碰撞在物面的位置(s0,s1,s2,…,sn),此处si表示碰撞点距离驻点的物面曲线距离,为了得到函数s=s(y),根据这2组数据进行代数插值,得到局部收集系数是s关于y的一阶导数,采用三次样条插值。
函数s(y)在子区间[yi-1,yi]上的表达式si(y)是次数不高于3的代数多项式,所以si*(y)是线性函数,记
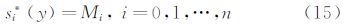
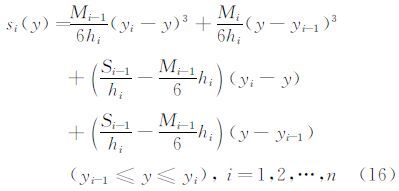
相应地,局部收集系数sl′(y)的表达式为
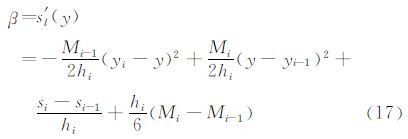
图 6所示为实验用有机玻璃圆柱,外径为30mm,厚为5mm,高为150mm。在结冰实验条件下,将实验模型固定在支架上,实验过程中取较低的实验温度并使实验模型能充分预冷,保证水滴在物面碰撞后即可冻结。实验过程中取风速为5m/s,温度为-8℃,空心圆柱置于LWC=0.59g/m3处,结冰时间为5min。为减小实验误差对同种工况下结冰进行4次实验。

|
| 图 6 实验圆柱 Fig. 6 Experimental cylinder |
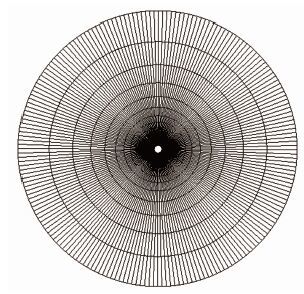
图 7所示为数值计算网格。计算条件与实验条件相同,计算采用O型网格,网格数量为6584。
|
| 图 7 计算网格 Fig. 7 Mesh for computation |
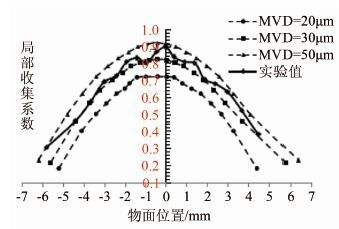
图 8所示为实验获得的局部收集系数曲线与数值仿真计算获得的MVD=20μm、MVD=30μm及MVD=50μm的局部收集系数曲线的比较。可以发现,实验获得的局部收集系数曲线介于MVD=30μm与MVD=50μm的局部收集系数曲线之间,可以推断出该喷雾系统产生的水滴粒子介于30~50μm之间,满足常规实验要求。
|
| 图 8 实验与计算对比 Fig. 8 Comparison of experiment and calculation |
为了研究风力机结冰与防除冰问题,本研究设计了一种利用自然低温条件的简便低成本的风力机结冰风洞试验系统。通过在冬季进行的验证实验,该结冰风洞的主要参数:实验段温度稳定性、液态水滴含量分布与液滴平均粒径等均在一定程度上满足实验需求,可利用其对风力机的叶片等进行结冰特性与防除冰技术研究。本研究提出的这种方法也可以为研究其他结构的结冰问题提供借鉴和参考。
| [1] | 何玉林, 李俊, 董明洪, 等. 冰载对风力机性能影响的研究 [J].太阳能学报, 2012, 33(9):1490-1496. He Y L, Li J, Dong M H, et al. Research the effect of wind turbine performance under icing conditions[J]. Acta Energiae Solaris Sinica, 2012,33(9): 1490-1496. |
| [2] | 朱程香, 王珑, 孙志国, 等. 风力机叶片翼型的结冰数值模拟研究[J].空气动力学学报, 2011,29(4):522-528. Zhu C X, Wang L, Sun Z G, et al. Numerical study of wind turbine blade airfoil ice accretion[J]. Acta Aerodynamica Sinica, 2011, 29(4):522-528. |
| [3] | Wang X. Convective heat transfer and experimental icing aerodynamics of wind turbine blades[D]. Maniboba: Department of Mechanical and Manufacturing Engineering of University of Manitoba,2008. |
| [4] | Frohboese P, Anders A. Effects of icing on wind turbine fatigue load[J]. Journal Physics: Conference Series,2007,(75): 0120361. |
| [5] | 孙少华, 徐洪雷, 符鹏程, 等. 叶片覆冰对风电机组的影响[J]. 风能, 2014, (9):100-103. Sun S H, Xu H L, Fu P C, et al. Effect of blade icing on wind turbine[J]. Wind Energy, 2014, (9):100-103. |
| [6] | Shin J, Bond T. Results of an icing test on a NACA 0012 airfoil in the NASA Lewis Icing Research Tunnel[R]. NASA TM-105374,1992. |
| [7] | Shin J, Bond T. Experimental and computational ice shapes and resulting drag increase for a NACA0012 airfoil[R]. NASA TM-105743,1992. |
| [8] | Vecchione L, De Matteis P, Leone G. An overview of the CIRA icing wind tunnel[R]. AIAA-2003-0900, 2003. |
| [9] | 邢玉明, 盛强, 常士楠.大型开式冰风洞的模拟技术研究[C]//大型飞机关键技术高层论坛暨中国航空学会2007年学术年会论文集, 深圳:2007:1-10. Xing Y M, Sheng Q, Chang S N. Study on simulation technology of large open ice wind tunnel[C]//China Aviation Society of the Key Technologies of Large Aircraft in 2007, Shenzhen: 2007: 1-10. |
| [10] | 易贤, 桂业伟, 肖春华, 等. 结冰风洞液态水含量测量方法研究[J]. 科技导报, 2009, 27(21):86-90. Yi X, Gui Y W, Xiao C H, et al. A method of liquid water content measurement in icing wind tunnel[J]. Science & Technology Review, 2009, 27(21):86-90 |
| [11] | 易贤, 桂业伟, 杜雁霞, 等. 结冰风洞水滴直径标定方法研究[J]. 实验流体力学, 2010, 24(5):36-41. Yi X, Gui Y W, Du Y X, et al. Study on the method of droplet diameter calibration in icing wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5):36-41. |
| [12] | 易贤.飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳:中国空气动力研究与发展中心, 2007. Yi X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. |



