飞机结冰是飞行实践中经常遭遇的一种物理现象,也是导致飞行安全隐患的主要因素之一[1, 2],由于结冰环境的不同,结冰的类型也有所差异,典型的结冰类型包括霜冰、明冰与混合冰[3]。结冰风洞试验是进行飞机结冰和防除冰研究的主要手段。与常规风洞试验一样,进行结冰风洞试验,必须遵循一定的相似准则。由于影响结冰的因素除了空气流场之外,还包括结冰云雾条件和飞行状态等,因此结冰试验相似准则远比常规风洞试验所要求的相似准则复杂。由于这种复杂性,从结冰风洞建立之初,国外就开始了针对结冰试验相似准则的研究[4, 5, 6, 7, 8, 9],国内近年来也在相关领域开展了一些研究工作[3, 10]。经过研究者们多年的努力,目前的相似准则已经可以完全适用于霜冰(Rime Ice)的模拟,但在模拟明冰(Glaze Ice)和混合冰(Mixing Ice)时,参考冰形与试验冰形之间始终存在一定程度的差异[11],使得现有相似准则应用的普适性受到限制。
与霜冰形成完全是干模式结冰不同,明冰及混合冰的生长过程是典型的湿模式结冰[12],其伴随着液态水膜的形成、生长及其与冰层的相互作用。对这一复杂过程的描述,目前广泛采用的是Messinger提出的模型[13],该模型基于热力学的分析方法,只从宏观上考虑了结冰过程的能量平衡,不能刻画结冰相变过程的传热学效应,尤其是忽略了相变的时间效应。而目前采用的结冰试验相似准则对相变过程模拟的相似参数,均来源于Messinger模型,这也是在明冰和混合冰试验中,参考冰形与试验冰形之间始终存在一定程度的差异的原因。针对该问题,本文基于结冰过程液/固相变的基本理论[14, 15, 16],对飞机结冰过程的液/固相变传热特性进行了分析和研究,提出一个考虑相变时间效应的结冰试验相似参数CT,并采用数值手段对该相似参数的有效性进行计算评估。
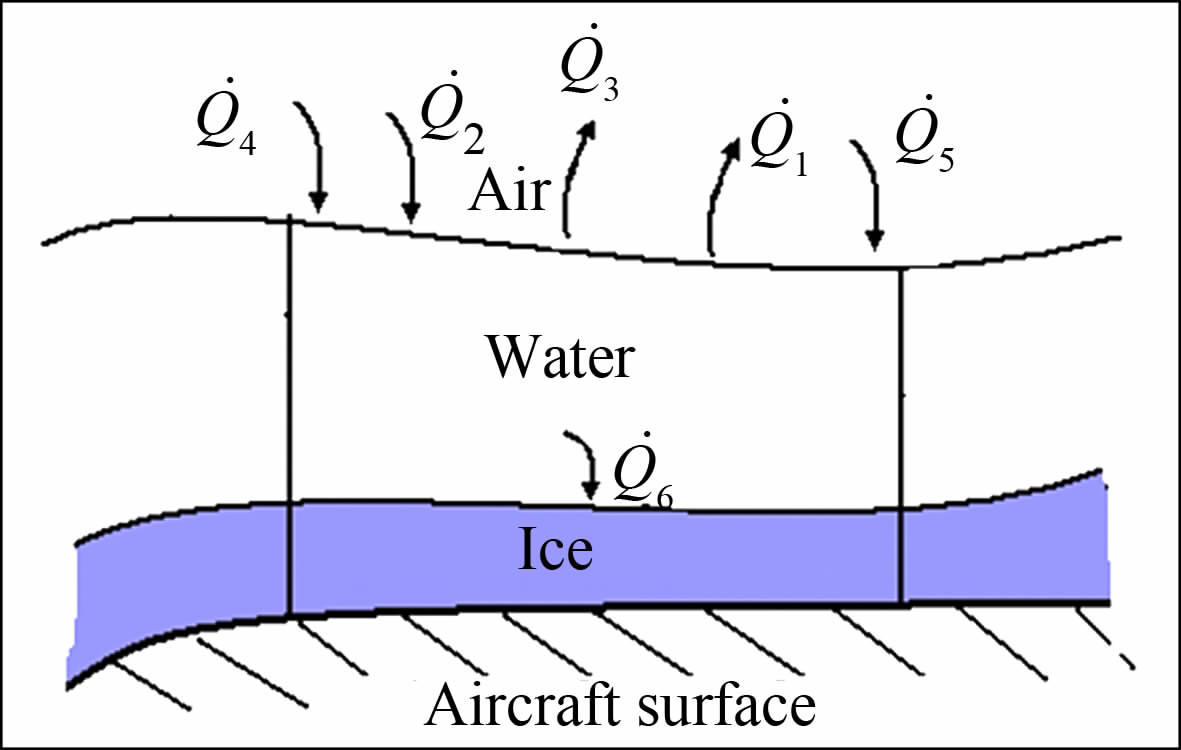
1 基于Messinger模型的结冰热力学相似参数考虑结冰表面上某控制体积中的能量传递情况,Messinger将能量传递分成6项[13],如图 1所示,则根据热力学第一定律,控制体积表面的能量平衡方程可以写成:
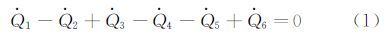
|
| 图 1 结冰表面控制体积内的能量传递 Fig. 1 Heat transfer on icing surface |
方程(1)中,$\dot{Q}$1为气流与表面的对流换热,$\dot{Q}$2为空气摩擦对表面的加热,$\dot{Q}$3为水滴或积冰表面蒸发的热量,$\dot{Q}$4为撞击在表面的水滴本身所带有的热能,$\dot{Q}$5为撞击在表面的水滴所具有的动能而转化成的热,$\dot{Q}$6为水滴冻结成冰的相变过程所释放的热能,各项表达式分别为:
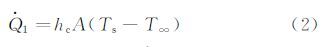





以上各式中:hc为对流传热系数,A为控制体积的表面积,Ts为冰表面温度,T∞为空气温度,rc为恢复因子,V∞为自由流速度,ca为空气比热,${\dot{m}}$va为蒸发液态水质量,hv为蒸发潜热,${\dot{m}}$im为与控制体积表面相碰撞的所有水滴的质量总和,cw为水的比热,${\dot{m}}$so是结冰的质量,hf为水的融解潜热。
将式(2)~(7)代入(1)可得:
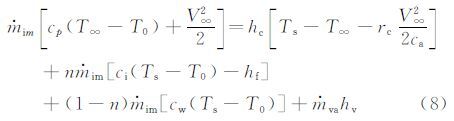
式中:T0为参考温度,T0=273.15K;ci为冰的比热;n为冻结比例,定义为表面某控制体积中冻结成冰的水质量与进入该控制体积的所有水质量的比值。对于明冰,将表面温度Ts=T0=273.15K代入式(8)并进行变换,可得到冻结比例表达式:
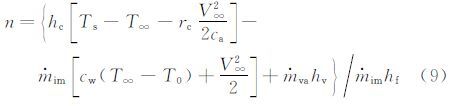
通常将式(9)写成如下形式:
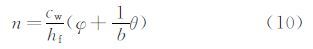
其中,φ为水滴能量传递势,其表达式为:
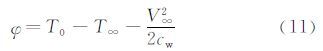
θ为空气能量传递势,可写成:
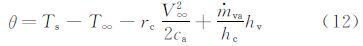
b为相对热因子,定义为:
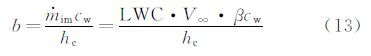
式中:LWC为液态水含量,β为收集系数。
冻结比例n,相对热因子b,空气、水滴的能量传递势θ和φ,是基于Messinger模型得到的结冰热力学相似参数,其中n和b均为无量纲参数,θ和φ则具有温度的量纲。为了使结冰过程的热力学特性相似,不同研究者定义了不同的相似参数及组合。AEDC的准则中有2个相似参数,分别为冻结比例n和水滴能量传递势φ,相似性要求为


其中下标“m”和“f”分别代表模型结冰的试验条件和全尺寸物体的参考结冰条件。ONERA的准则定义了2个相似参数,分别为热相对因子b和冻结比例n,其热力学过程的相似要求除了满足方程(14),还需满足

Messinger模型只从宏观上考虑了结冰过程的能量平衡,不能刻画结冰相变过程的传热学效应,尤其是忽略了相变的时间效应,基于该模型得到的相似准则在模拟明冰和混合冰方面始终存在不足。为此,本文尝试从传热学的角度推导相变的相似参数。
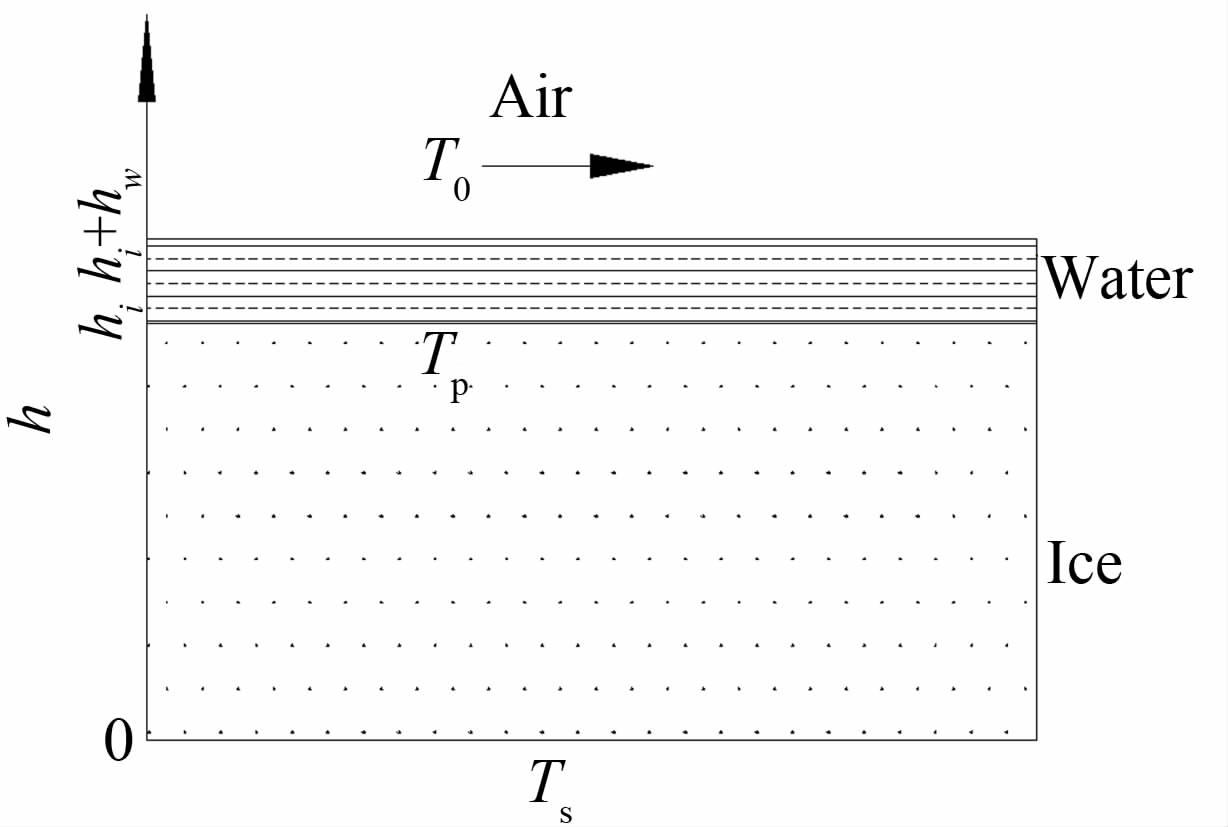
根据来流条件的不同,当空气中的过冷水滴撞击到飞机表面时,通常会出现表面无液膜和液/固共存的2种结冰现象,前者称为干模式结冰,后者称为湿模式结冰。由于干模式可以看作湿模式的特殊情况,为了使推导具有通用型,以湿模式作为推导对象,如图 2所示 ,一维相变传热过程可描述如下[14, 16]:
|
| 图 2 结冰表面物理模型 Fig. 2 Physical model of icing surface |
固相区和液相区:
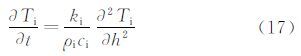
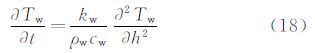
液/固相界面:
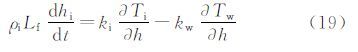
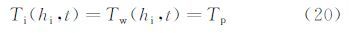
液/气相界面:
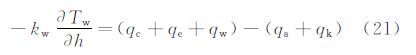
式中:qc为气流与表面的对流换热;qe为蒸发带走的热量;qw为撞击在表面的水滴自身携带的能量;qa为气动加热量;qk为撞击在表面的水滴所具有的动能。
质平衡方程:
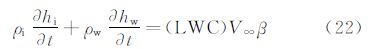
若将固、液相区的导热视为准稳态过程,对(17)和(18)式进行积分,并根据边界条件(20)和(21)式可得冰层和水膜的温度分布分别为
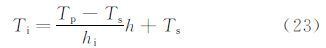
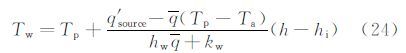
式中:q′source=qa+qk;${\bar{q}}$=αc+LWC·Vβcw+γeLe,αc为对流换热系数;γe为当量蒸发系数;Le为蒸发潜热。
将冰层生长过程分为液膜出现之前的干模式和液膜出现后的湿模式[14],并定义从干模式转变为湿模式的临界时间为tc,对质平衡方程(22)在湿模式区间(tc-t)进行积分得:
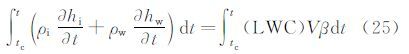
则湿模式阶段,水膜、冰层厚度与时间的关系为:
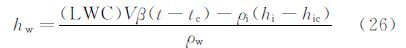
根据式(23)、(24)及液/固相界面能量方程(19)可得:
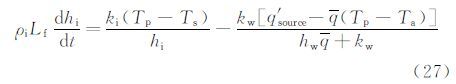
将(26)代入(27)式,即可获得冰层厚度随时间的变化关系:
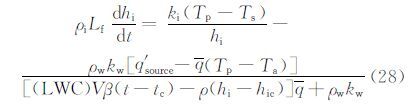
在水膜出现的临界点,有:
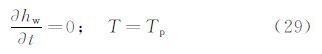
可得从干模式转变为湿模式的临界冰层厚度为:
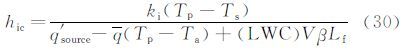
本文认为,对于2种相似的结冰,干模式转变为湿模式的无因次临界冰层厚度应相等,为此引入新的相似参数CT(临界厚度,Critical Thickness),定义

为相似参数,表征的是干模式转变为湿模式的无因次临界冰层厚度,其中L为特征尺寸,则相似性要求为
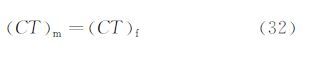
对于结冰试验,需要确定的试验参数共有7个,包括模型尺寸Lm、速度Vm、压力pm、水滴直径dm、液态水含量LWCm、结冰时间tm和温度Tm,而现有的结冰试验相似准则共有4个约束方程,因此在选取试验参数时可以自由指定3个,通常根据结冰风洞试验段大小指定试验模型尺寸,再自由给定速度和压力,其余试验参数则通过计算获得。以AEDC的相似准则为例,其确定试验参数的公式为[3]:
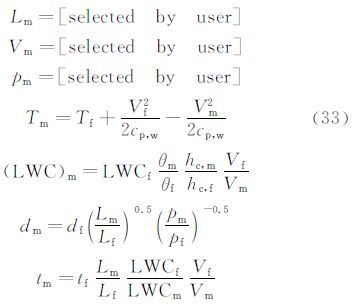
在实际应用中,通常以Weber数相等作为试验速度选取的条件,即:
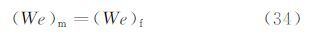
将新的相似参数CT引入,结合式(32)和(34)进行数值迭代求解,可使得压力与速度唯一确定,避免压力与速度选取的随意性。
4 相似参数的有效性评估采用数值方法对本文提出的相似参数的有效性进行评估,数值评估的主要思路为,计算2个几何相似且严格缩比翼型上的结冰,计算条件按新相似参数及式(33)确定的参数关系式进行选取。如果在2个翼型上得到的冰形也具有与物体几何尺寸同样的缩比比例,则认为相似参数是有效的。本文分别选用NACA0012翼型和某超临界翼型进行了数值仿真评估,数值计算的方法参见文献[3]。
4.1 NACA0012翼型NACA0012翼型的参考结冰条件为:特征尺寸1m,速度72m/s,压强101 325Pa,温度-7℃,水滴直径20μm,液态水含量0.5g/m3,结冰时间25min,由该条件计算的CT数为0.0069。表 1给出的是参考结冰条件以及按照式(32)、(33)和(34)所计算的1/2缩比模型的试验条件,表中“Reference”代表参考结冰条件,“Sacling”代表缩比的试验条件。
| Case | L/m | V/(m·s-1) | P/Pa | T/℃ | d/μm | LWC/(g·m-3) | t/min |
| Reference | 1 | 72 | 101325 | -7.0 | 20.0 | 0.50 | 25.0 |
| Scaling | 0.5 | 94.0 | 100412 | -7.4 | 11.7 | 0.65 | 7.3 |
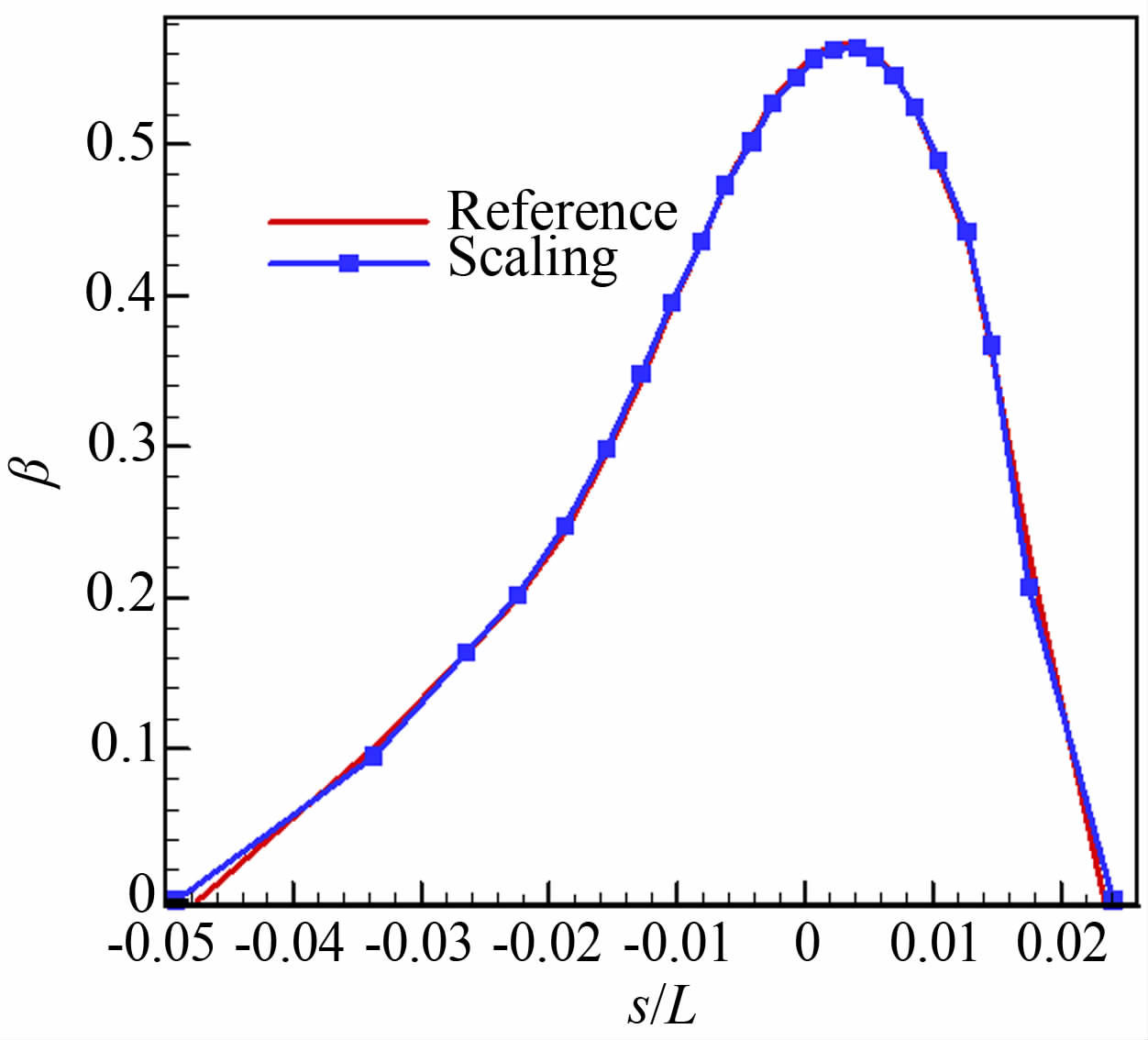
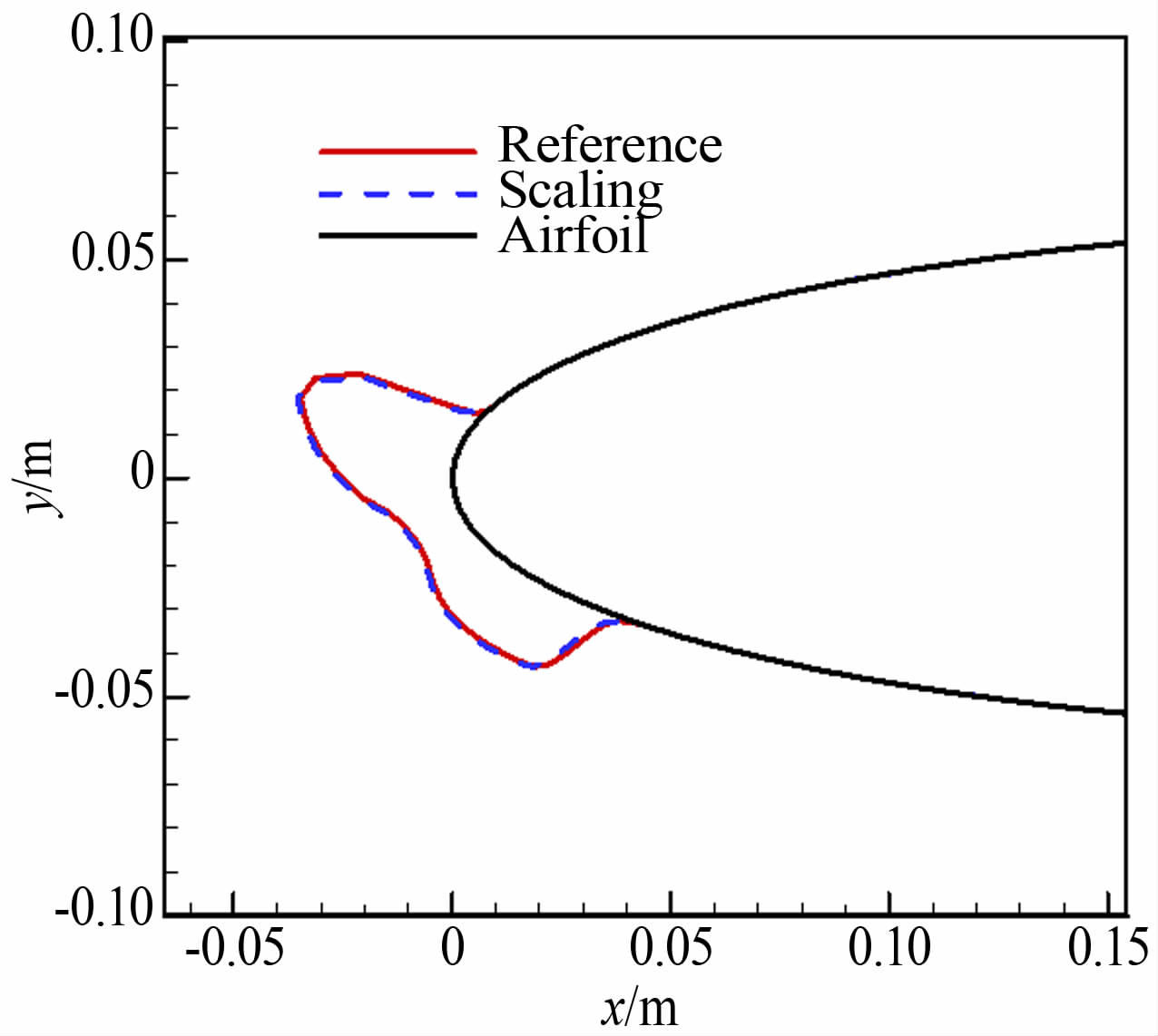
图 3给出的是参考状态和缩比状态下,翼面水滴收集率分布曲线,可以看到,除了在下翼面撞击极限附近有微小差别,2种状态的水滴收集率分布均保持一致;图 4显示的是将参考条件和缩比条件对应的冰形归一化之后的对比,可以发现,无论结冰的范围、冰的厚度和冰角位置等,二者均保持一致,说明按照表 1所给出的参数进行结冰,能够保证参考条件和试验条件具有一致的结冰外形。
|
| 图 3 试验条件与参考条件水滴收集率对比(NACA0012 翼型) Fig. 3 Comparison of collection efficiencies (NACA0012 airfoil) |
|
| 图 4 试验条件与参考条件结冰外形对比(NACA0012 翼型) Fig. 4 Comparison of ice shapes (NACA0012 airfoil) |
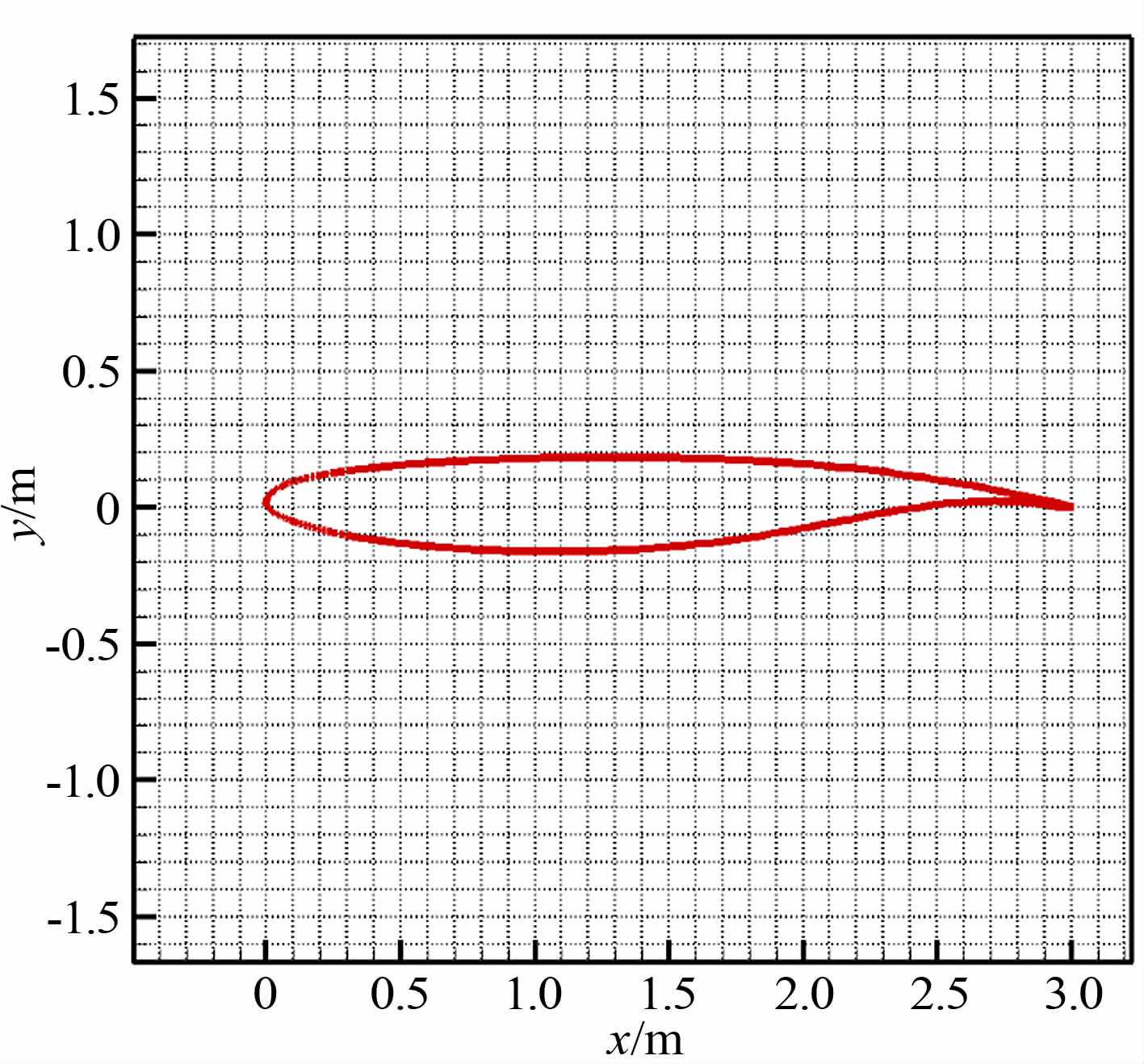
本文研究所采用的超临界翼型源自某型运输机机翼剖面,如图 5所示,该翼型弦长3m,最大厚度0.35m。
|
| 图 5 计算采用的超临界翼型(超临界翼型) Fig. 5 The supercritical airfoil for simulation (supercritical airfoil) |
超临界翼型的参考结冰条件为:特征尺寸3m,速度116m/s,压强84 606Pa,温度-8.8℃,水滴直径20μm,液态水含量0.54g/m3,结冰时间22.5min,由该条件计算的CT数为0.001,表 2给出的是参考结冰条件及其对应的1/2缩比模型的试验条件。
| Case | L/m | V/(m·s-1) | P/Pa | T/℃ | d/μm | LWC/(g·m-3) | t/min |
| Reference | 3 | 116 | 84606 | -8.8 | 20.0 | 0.54 | 22.5 |
| Scaling | 1.5 | 150.5 | 87585 | -9.9 | 11.9 | 0.72 | 6.5 |
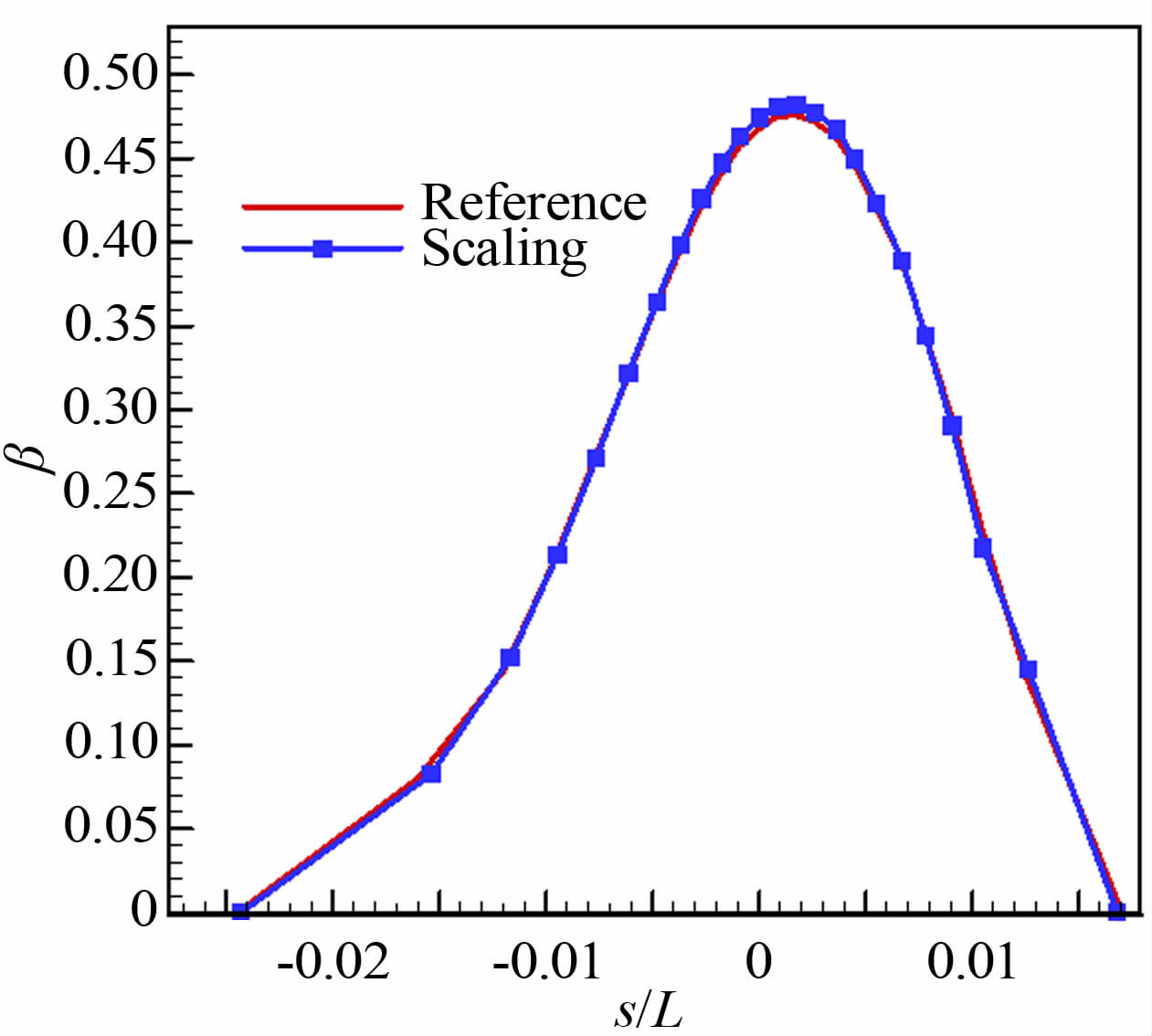
图 6给出的是水滴收集率分布曲线的对比,计算显示缩比条件与参考条件下的水滴收集率一致,由于水滴收集率主要决定于来流速度、水滴直径和空气密度,虽然缩比条件的水滴直径比参考条件小会导致水滴收集率降低,但是缩比条件中速度、密度的增加,以及模型尺寸的减小又会带来水滴收集率的增加,综合效应使得缩比条件与参考条件下的水滴收集率达到了一致。
|
| 图 6 试验条件与参考条件水滴收集率对比(超临界翼型) Fig. 6 Comparison of collection efficiencies (supercritical airfoil) |
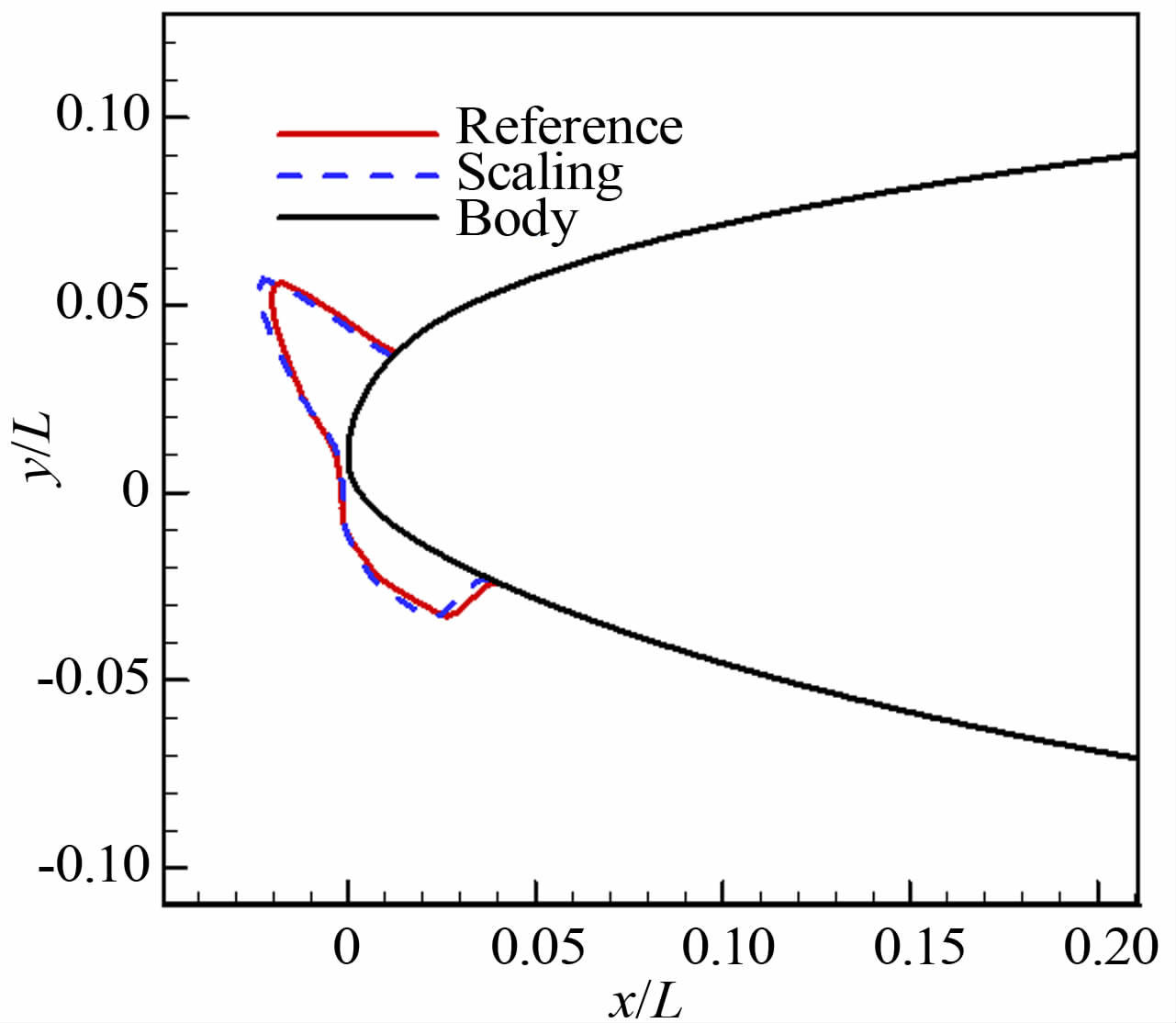
图 7给出的是结冰外形对比,可以看到:翼面形成的是典型明冰;2种条件对应的结冰在上翼面结冰极限以及驻点处的厚度完全相同;下翼面的结冰极限有微小差异,缩尺条件的结冰极限略小于参考条件;翼面下方的冰角保持一致,翼面上方的冰角有细微差异,缩尺条件的冰角比参考条件的冰角略大。总的说来,2种冰形在翼面的分布范围相同,冰的生长趋势和冰形轮廓总体上是一致的。说明按照表 2的缩尺结冰条件,能够得到与参考冰形相似的结冰。
|
| 图 7 缩尺条件与参考条件结冰外形对比(超临界翼型) Fig. 7 Comparison of ice shapes (supercritical airfoil) |
基于结冰过程的传热模型,提出了一个考虑相变时间效应的结冰试验相似参数CT,并采用数值方法进行了验证评估,得到如下结论:
(1)从结冰相变的传热学过程所推导的新相似参数,与基于Messinger结冰热力学模型所推导的相似参数有明显区别,其显著特征是考虑到了结冰的干模式和湿模式,体现了相变的时间效应;
(2)通过将新的相似参数引入到现有结冰试验相似准则中,结合等Weber数的试验速度选取原则,可使得试验压力与速度唯一确定,避免了压力与速度选取的随意性;
(3)数值仿真评估结果说明,采用本文提出的相似参数及相应的试验参数确定方法,能够得到与参考条件一致的水滴收集率和结冰,初步说明新相似参数的是有效的;
(4)飞机结冰,尤其是包含湿模式的结冰,涉及到复杂环境下的空气和液态水流动、传热传质与相变,本文工作是对湿模式结冰精确模拟试验理论的初步探索,虽然初步结果让人满意,但还需进一步深入和完善,尤其需要开展大量的实验验证工作。
| [1] | Cebeci T, Kafyeke F. Aircraft icing[J]. Annual Review of Fluid Mechanics, 2003, 35:11-21. |
| [2] | Bragg M B, Broeren A P, Blumenthal L A. Iced-airfoil aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41(5):323-362. |
| [3] | 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳:中国空气动力研究与发展中心,2007. Yi X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. |
| [4] | Charpin F, Fasso G. Icing testing in the large modane wing-tunnel on full-scale and reduced scale models[R]. NASA-TM-75737, 1979. |
| [5] | Ruff G A. Analysis and verification of the icing scaling equations[R]. AEDC-TR-85-30, 1985. |
| [6] | Ruff G A. Verification and application of the icing scaling equations[R]. AIAA-86-0481,1986. |
| [7] | Anderson D N. Rime-, mixed-, and glaze-iced evalutions of three scaling laws[R]. AIAA-94-0718, 1994. |
| [8] | Anderson D N. Methods for scaling icing test conditions[R]. AIAA-95-0540, 1995. |
| [9] | Anderson D N. Further evaluation of traditional icing scaling methods[R]. AIAA-96-0633, 1996. |
| [10] | 易贤, 朱国林, 桂业伟. 一种改进的积冰试验相似准则及其评估[J]. 实验流体力学, 2008, 22(2): 84-87. Yi X, Zhu G L, Gui Y W. Modification and evaluation of an icing scaling law[J]. Journal of Experimentals in Fluid Mechanics, 2008, 22(2): 84-87. |
| [11] | Anderson D N. Manual of scaling methods[R]. NASA/CR-2004-212875, 2004. |
| [12] | 杜雁霞, 桂业伟, 肖春华, 等. 飞机结冰过程的液/固相变传热研究[J]. 航空动力学报, 2009, 24(8): 1824-1829. Du Y X, Gui Y W, Xiao C H, et al. Investigation on solid-liquid phase change heat transfer of aircraft icing[J]. Journal of Aerospace Power, 2009,24(8):1824-1829. |
| [13] | Messinger B L. Equilibrium temperatuer of an unheated icing surface as a function of airspeed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29-42. |
| [14] | Myers T G. An extension to the messinger model for aircraft icing[J]. AIAA Journal, 2001, 39(2): 211-218. |
| [15] | 易贤, 桂业伟, 朱国林. 飞机三维结冰模型及其数值求解方法[J]. 航空学报, 2010, 31(11): 2152-2158. Yi X, Gui Y W, Zhu G L. Numerical method of a three-dimensional ice accretion model of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2152-2158. |
| [16] | Du Y X, Gui Y W, Xiao C H, et al. Investigation on heat transfer characteristics of aircraft icing including runback water[J]. International Journal of Heat and Mass Transfer, 2010, 53: 3702-3707. |



