2. 同济大学土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
随着社会经济的不断发展,为了追求快速的交通路径,在跨河跨海大桥方面,桥梁结构朝着大跨轻柔的方向发展。大跨轻柔结构对风致振动提出较高的要求,特别是对桥梁颤振。20世纪末,中央开槽作为一种气动措施被提出来,但没有应用到实际工程中去。西堠门大桥[1]是一座真正意义上为改善结构的气动性能而采用中央开槽钢箱梁的悬索桥,使得箱梁桥的颤振性能显著提高。
关于大跨度悬索桥中央开槽断面的颤振分析,很多学者得出了相近结论。日本学者Hiroshi Sato等[2]在对1991m主跨的明石海峡大桥气动稳定性分析研究中,得出桥梁断面中央开槽措施在改善断面气动稳定性上效果显著;Larsen[3]认为随着槽宽比的增大,桥梁断面抵抗颤振的能力越强;曹丰产[4]运用CFD方法分析了头部形状和开槽宽度对颤振性能的影响,得出不是所有开槽宽度都有利于颤振稳定;杨詠昕[5]和邹小洁[6]认为中央开槽断面对颤振稳定存在很大的影响,且存在一个最优槽宽比,只有在最优槽宽比时才能体现出中央开槽措施的优势;对于气动导数识别,张若雪[7]认为流线型较好的断面,颤振导数只与断面的几何外形有关。
国内外学者的研究给出中央开槽有利于提高颤振性能的定性结论,没给出各关键参数对颤振性能影响的分析。在风洞试验中,模型控制是由关键参数模拟得出的,分体双箱梁的横梁连接对于桥梁的整体稳定性起到了很大的作用等。在颤振分析过程中涉及到多项关键参数的共同作用,因此有必要对关键参数给出单独颤振分析。本文从开槽比、质量参数、弯扭频率和纵向遮盖率4项关键参数出发,分析其对颤振性能的影响。在槽宽比和纵向遮盖率的参数分析上,得出颤振临界风速变化曲线,曲线峰值对应最优开槽比。在质量参数和弯扭频率参数上,对颤振性能影响做了定量分析,得出颤振性能对各参数的敏感度不同。
1 节段模型风洞试验研究本文以浙江舟山西堠门大桥为背景。在同济大学土木工程防灾国家重点实验室TJ-1边界层风洞中进行试验,TJ-1风洞为全钢结构的开口式直流边界层风洞,风洞试验段尺寸为1.8m(宽)×1.8m(高)×12m(长)。试验在均匀流场中模拟竖向和扭转2个自由度的振动。
试验通过调节节段模型的开槽宽度和纵向遮盖长度来控制开槽比和纵向遮盖率。设定0%、20%、30%、40%、60%、80%、100% 7种开槽比D/B(其中D为开槽宽度,B为未开槽节段宽度),0%、12.5%、25%、37.5% 4种纵向遮盖率3l/L(l为每个横梁遮盖长度,L为节段总长度)。对20%、30%、40%的开槽断面进行4种纵向遮盖下的颤振试验,对60%、80%、100%的开槽断面进行0%、25% 2种纵向遮盖下的颤振试验,并依照规范进行+3°、0°、-3° 3种迎角试验[8]。试验共49个工况。
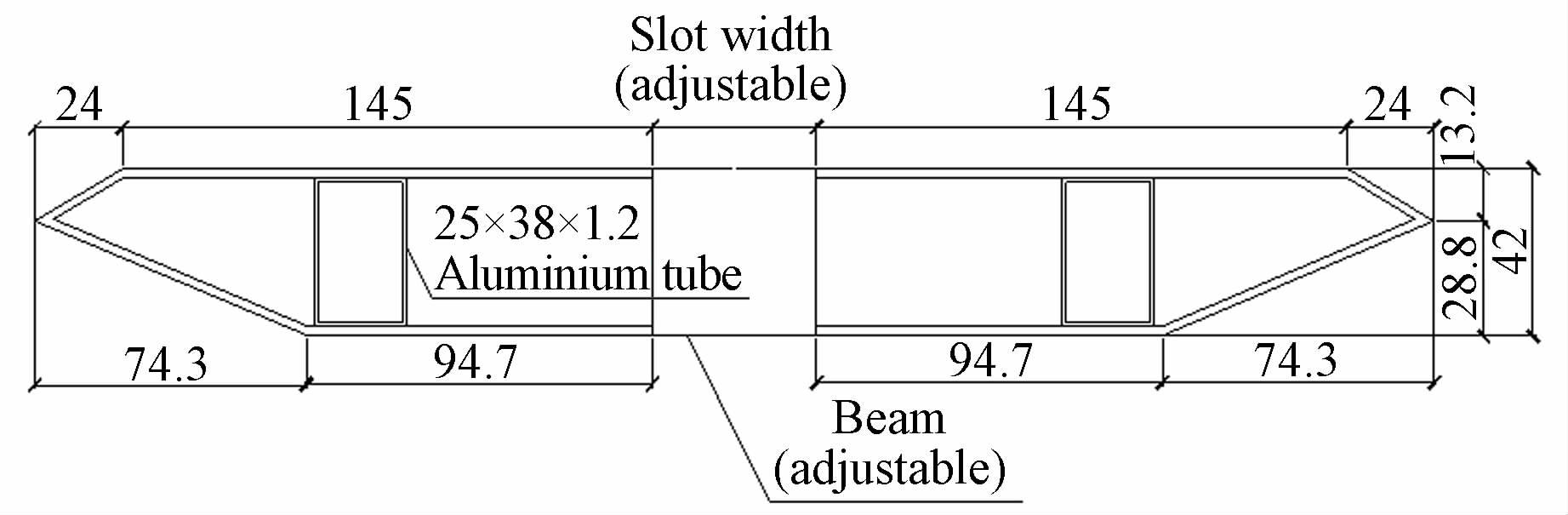
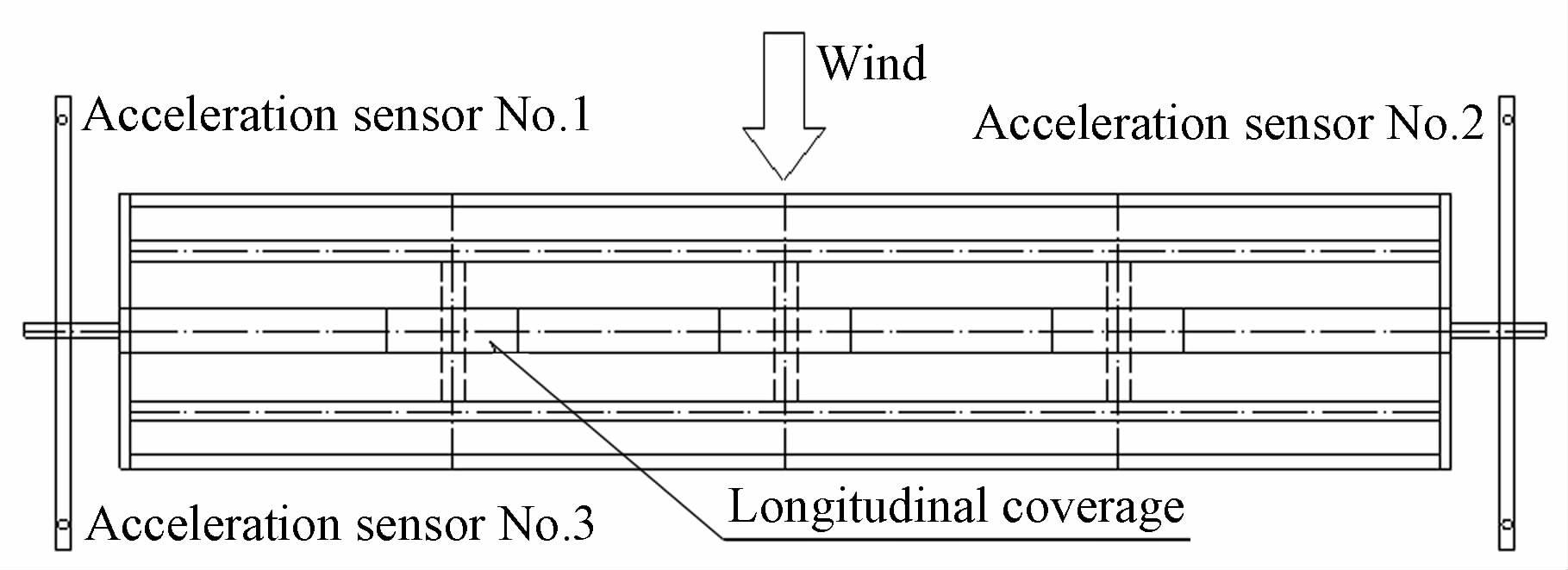
未开槽节段主要模型参数为:质量M=5.165kg/m、质量惯矩Im=0.06506(kg·m2)/m、宽度B=0.338m、高度H=0.042m、竖弯频率fh=1.172Hz、扭转频率ft=3.174Hz、模型缩尺比i=1∶80。试验是研究成桥状态下4项关键参数对颤振性能的影响,基于片条假定,将主缆、吊杆、护栏及其他附属设施等对结构模态的贡献等效在主梁上。模型横断面如图 1所示、加速度布置图和现场试验图如图 2、3所示。
|
| 图 1 中央开槽钢箱梁节段模型横断面图(单位:mm) Fig. 1 Section model of central slotted steel box girder (Unit: mm) |
|
| 图 2 节段模型加速度传感器布置图 Fig. 2 Layout of acceleration sensors for section model |

|
| 图 3 节段模型颤振试验模型装置 Fig. 3 Device of section model flutter test |
利用自由振动法与修正的最小二乘法颤振导数识别程序[9],对中央开槽钢箱梁做节段模型颤振试验和颤振导数的识别。
试验共49个工况,对应49组颤振导数。现以0%开槽比0°迎角工况的颤振导数为例,说明颤振导数随折减风速的变化趋势,如图 4所示。

|
| 图 4 西堠门大桥钢箱梁断面颤振导数 Fig. 4 Flutter derivatives of steel girder section for Xihoumen Bridge |
二维颤振数值模型的运动方程为:
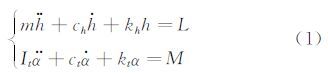
其中,m和It为桥梁节段模型的延米质量和质量惯矩;kh和kt分别为模型的竖弯和扭转刚度;ch和ct分别为模型的竖弯和扭转阻尼比,L和M分别为模型的延米气动升力和升力矩。Scanlan[10, 11]气动自激力为:
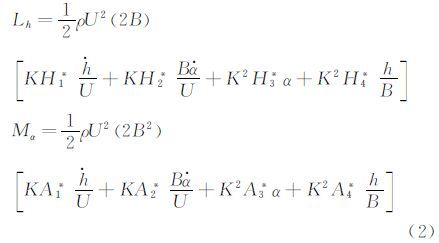
其中,U为平均风速,ρ为空气密度,B为模型宽度,K为无量纲折减频率,h和α分别为模型的竖向和扭转位移,Hi*和Ai*(i=1,2,3,4)分别为竖弯、扭转颤振导数。将(2)式代入(1)式,可得:
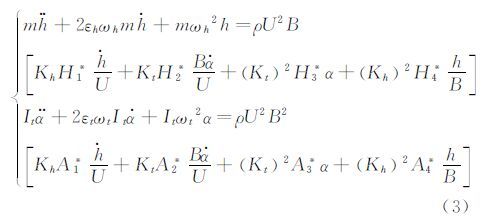
令

将(4)式代入(3)式后,二维颤振问题转化为求解(5)式的复特征值和特征向量问题:
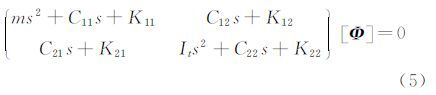
进而转化为求解一元四次方程:
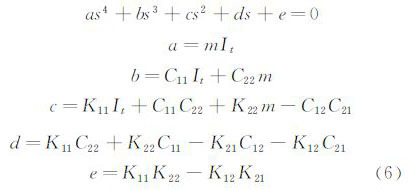
因一元四次方程有解析解,本文基于二维颤振复模态特征值直接分析方法(Straight Forward Method),获得方程的特征值如下:
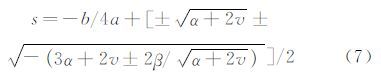
特征值可表示成s=(-ζ+i)ω,其中ω为圆频率,且为正值。当s=(0+i)ω时,全桥阻尼为0,颤振发生。
2.2 各工况颤振临界风速由于该节段模型流线型较好,节段模型的物理参数对颤振导数的数值不产生影响,颤振导数只与节段模型的几何形状有关,故保持除槽宽比和遮盖率之外的其他物理参数不变,采用基于MATLAB编程的二维颤振复模态特征值直接分析方法[12, 13],对风洞试验识别出的颤振导数进行二维耦合颤振分析,计算出49组颤振导数所对应的49项颤振临界风速,如表 1所示,其中未显示数据为导数无法识别所致。
| 槽宽比 | 纵向遮盖率 | 颤振临界风速/(m·s-1) | 最不利风速/(m·s-1) | ||
| +3°迎角 | 0°迎角 | -3°迎角 | |||
| 0% | ---- | 83 | 97 | ---- | 83 |
| 20% | 0.00% | 91 | 125 | 137 | 91 |
| 12.50% | 95 | 122 | 131 | 95 | |
| 25% | 84 | 114 | 118 | 84 | |
| 37.50% | 75 | 90 | 128 | 75 | |
| 30% | 0.00% | 101 | 129 | ---- | 101 |
| 12.50% | 102 | 126 | ---- | 102 | |
| 25.00% | 98 | 121 | ---- | 98 | |
| 37.5% | 105 | 113 | ---- | 105 | |
| 40% | 0.00% | 112 | 124 | 134 | 112 |
| 12.50% | 113 | 124 | 119 | 113 | |
| 25% | 94 | 134 | ---- | 94 | |
| 37.50% | 78 | 109 | 124 | 78 | |
| 60% | 0.00% | 106 | 111 | ---- | 120 |
| 25% | 117 | 125 | 138 | 117 | |
| 80% | 0.00% | 95 | 99 | ---- | 95 |
| 25% | 92 | 105 | 107 | 92 | |
| 100% | 0.00% | 91 | 94 | ---- | 91 |
| 25.00% | 89 | 92 | 102 | 89 | |
选取在0%遮盖率和25%遮盖率情况下,分析不同开槽比对颤振性能的影响,如图 5所示。

|
| 图 5 不同开槽比节段模型颤振临界风速 Fig. 5 Critical flutter wind speed of section model with different slot ratio |
从图中可以明显看出,颤振临界风速随槽宽比的增加,呈现先增大后减小的趋势。在仅有开槽比一种改变因素时,分体双箱梁颤振临界风速曲线均在某一开槽比时取得极大值,即最优开槽比,如0%遮盖率2工况临界风速最大分别为113.6和129.1m/s,增长率为36.9%和33.1%,可见中央开槽对于提高颤振临界风速效果显著。0%和25%遮盖率对应最优槽宽比分别为45%和60%。25%遮盖率2个工况的峰值相对0%遮盖率的峰值整体向右平移,可以认为增加横梁纵向遮盖使得气流通过开槽的面积变小,相当于减小了一部分开槽比,致使颤振临界风速峰值右移。
从表 1还可看出每种开槽比,+3°、0°、-3°迎角工况颤振临界风速依次增大。+3°迎角为最不利迎角,对应临界风速为最不利风速。
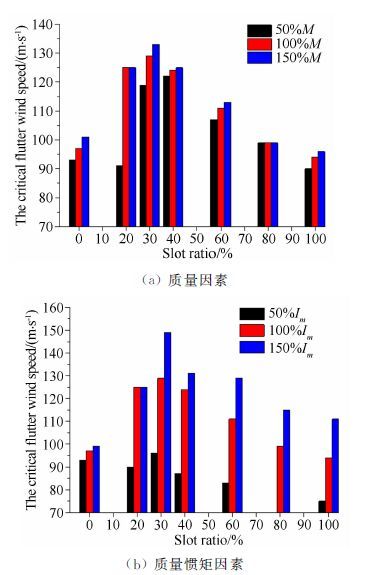
3.2 质量参数实际工程应用中在进行槽宽比的优化选型时,改变槽宽比不止会影响结构的几何外形,同时会在较大程度上改变结构的质量参数,比如质量和质量惯距。质量参数对颤振临界风速的影响鲜有研究。张若雪[7]的研究认为,流线型较好的截面,其颤振导数只与断面的几何外形有关,模型的物理参数对颤振导数无影响。基于此结论,本文利用风洞试验的模型和颤振导数,在数值算法中分别增加和减少模型质量M和质量惯矩Im,得到二者对颤振性能的影响。选取0%遮盖率0°迎角的各工况,改变模型质量M和质量惯矩Im为原值的50%和150%,控制其他参数不变。数值分析结果如表 2和图 6所示,表中临界风速单位为m/s。
| 槽宽比 | 0% | 20% | 30% | 40% | 60% | 80% | 100% | |
| 质量因素 | 2.5825(50%) | 93 | 91 | 119 | 122 | 107 | 99 | 90 |
| 5.165 | 97 | 125 | 129 | 124 | 111 | 99 | 94 | |
| 7.7475(150%) | 101 | 125 | 133 | 125 | 113 | 99 | 96 | |
| 质量惯矩因素 | 0.03253(50%) | 93 | 90 | 96 | 87 | 83 | 64 | 75 |
| 0.06506 | 97 | 125 | 129 | 124 | 111 | 99 | 94 | |
| 0.09759(150%) | 99 | 125 | 149 | 131 | 129 | 115 | 111 | |
| 注:表中较高临界风速是人为改变参数得到的,更便于对比分析;试验存在偶然误差。 | ||||||||
|
| 图 6 质量参数对颤振性能的影响 Fig. 6 Effect of mass parameter on flutter stability |
从表 2和图 6可以得出,随着质量、质量惯矩的增大,临界风速不断增大,且质量惯矩的变化幅度较质量因素变化大。
3.3 弯扭频率同样,分析弯扭频率对颤振性能的影响,与分析质量参数时的原理一样,由于气动导数只与断面的几何形状有关,可以使用原始模型和颤振导数。选取0%遮盖率0°迎角的各工况,改变竖弯基频fh和扭转基频ft为原值的50%和150%,控制其他参数不变。数值分析结果如表 3和图 7所示,表中临界风速单位为m/s。
| 槽宽比 | 0% | 20% | 30% | 40% | 60% | 80% | 100% | |
| 竖弯基频因素 | 0.586(50%) | 102 | 125 | 145 | 130 | 119 | 105 | 96 |
| 1.172 | 97 | 125 | 129 | 124 | 111 | 99 | 94 | |
| 1.758(150%) | 95 | 96 | 121 | 114 | 101 | 82 | 94 | |
| 扭转基频因素 | 1.587(50%) | 49 | 43 | 58 | 54 | 49 | 54 | 59 |
| 3.174 | 97 | 125 | 129 | 124 | 111 | 99 | 94 | |
| 4.761(150%) | 145 | 188 | 208 | 196 | 175 | 126 | 104 | |
| 注:表中较高临界风速是人为改变参数得到的,更便于对比分析;试验存在偶然误差。 | ||||||||

|
| 图 7 弯扭频率对颤振性能的影响 Fig. 7 Effect of torsional and bending frequency on flutter stability |
从表 3和图 7中可以明显得出,随着扭转频率的增大,临界风速不断增大;相反,竖弯频率的增大会引起颤振性能的下降。对颤振临界风速的变化幅度影响而言,扭转频率相比竖弯频率较大。
综合分析质量参数和弯扭频率因素,不同参数对颤振性能的影响程度不一样,即颤振性能对各个参数的敏感度不同。颤振性能对以上几项关键参数的敏感度从小到大依次为:质量、竖弯基频、质量惯矩、扭转频率,因此在今后的大跨度桥梁设计中更要注重分体双箱梁截面的抗扭转设计。
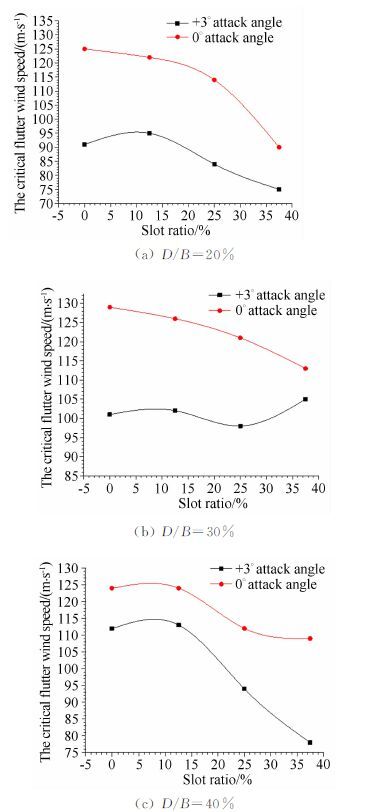
3.4 纵向遮盖率控制其他条件不变改变纵向遮盖率,单独分析纵向遮盖的影响,如图 8所示。
|
| 图 8 颤振临界风速随纵向遮盖率的变化规律 Fig. 8 Critical flutter wind speed versus longitudinal coverage ratio |
从上图不能得出纵向遮盖对颤振性能影响的统一规律,但可以肯定不是所有遮盖率都有利于颤振稳定,如开槽比40%时,随着遮盖率的增大颤振临界风速急剧减小。对于每种开槽宽度存在一个最优纵向遮盖率,开槽比为20%、30%和40%开槽比时的最优遮盖率分别为12.5%、37.5%和12.5%,且20%和40%开槽比时变化趋势相似。
4 结 论基于风洞试验数据和数值算法综合研究,对大跨度中央开槽悬索桥钢箱梁断面的颤振关键参数进行了研究,包括几何参数、质量参数、频率参数等,得出了如下主要结论:
(1) 槽宽比的影响:颤振临界风速随槽宽比的增加,先增大后减小,各工况均存在最优开槽比,颤振临界风速增长率高达37%。横梁纵向遮盖相当于减少了一部分开槽宽度。+3°、0°、-3°迎角颤振临界风速依次增大,+3°迎角为最不利迎角,对应临界风速为最不利风速。
(2) 质量参数的影响:相同槽宽比时,随着质量、质量惯矩的增大,临界风速不断增大,且质量惯矩造成的临界风速变化幅度较质量因素变化大。
(3) 频率参数的影响:随着扭转频率的增大,颤振临界风速不断增大;相反,竖弯频率的增大会引起颤振性能的下降。对颤振临界风速的变化幅度影响而言,扭转频率相比竖弯频率较大。
(4) 参数敏感性:颤振临界风速对各个参数的敏感度不同,敏感度从小到大依次为:质量、竖弯基频、质量惯矩、扭转频率。在开槽钢箱梁选型阶段,除要注意槽宽比的选择外,不能忽视其它因素的影响。
(5) 遮盖率的影响:对于每种开槽宽度存在一个最优纵向遮盖率,开槽比为20%、30%和40%开槽比时的最优遮盖率分别为12.5%、37.5%和12.5%,且20%和40%开槽比时变化趋势相似。
| [1] | 葛耀君. 大跨度悬索桥抗风[M]. 北京:人民交通出版社, 2011. Ge Yaojun. Wind resistance of long span suspension bridges[M]. Beijing:China Communication Press, 2011. |
| [2] | Sato H, Ogihara K. Aerodynamic characteristics of slotted box girders[C]. The Hong Kong Institution of Engineers. Proceedings of Bridges into 21st Century. Hong Kong:The Hong Kong Institution of Engineers, 1995:721-728. |
| [3] | Larsen A. Aeroelastic considerations for the gibraltar bridge feasibility study[M]//Bridge Aerodynamics. Rotterdam:Balkema, 1998:165-173. |
| [4] | 曹丰产. 桥梁断面中间开槽对颤振稳定性的影响[J]. 同济大学学报, 2002, 30(5):551-556. Cao Fengchan. Influence of central slot on bridge box girder's flutter instability[J]. Journal of Tongji University, 2002, 30(5):551-556. |
| [5] | 杨詠昕, 葛耀君, 曹丰产. 大跨度悬索桥中央开槽箱梁断面的颤振性能[J]. 中国公路学报, 2007, 20(3):35-40. Yang Yongxin, Ge Yaojun, Cao Fengchan. Flutter performance of central-slotted box girder section for long-span suspension bridges[J]. China Journal of Highway and Transport, 2007, 20(3):35-40. |
| [6] | 邹小洁, 杨詠昕, 葛耀君. 大跨度悬索桥钢箱加劲梁中央开槽的颤振控制机理[J]. 力学季刊, 2007, 28(2):187-194. Zou Xiaojie, Yang Yongxin, Ge Yaojun. Flutter mitigation of long span suspension bridges with central slotted box girders[J]. Chinese Quarterly of Mechanics, 2007, 28(2):187-194. |
| [7] | 张若雪. 桥梁结构气动参数识别的理论和实验研究[D]. 上海:同济大学, 1998. Zhang Ruoxue. Theoretical and experimental study on identification of aerodynamic parameters of bridge decks[D]. Shanghai:Tongji University, 1998. |
| [8] | 中华人民共和国交通部. JTG/T D60-01-004公路桥梁抗风设计规范[S]. 北京:人民交通出版社, 2004. Ministry of Transport of the People's Republic of China. JTG/T D60-01-004 Wind-resistent design specification for highway bridges[S]. Beijing:China Communication Press, 2004. |
| [9] | 丁泉顺, 陈艾荣, 项海帆. 桥梁断面气动导数识别的修正最小二乘法[J]. 同济大学学报, 2001, 29(1):25-29. Ding Quanshun, Chen Airong, Xiang Haifan. Modified least-square method for identification of bridge deck aerodynamic derivatives[J]. Journal of Tongji University, 2001, 29(1):25-29. |
| [10] | Scanlan R, Tomko J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, 1971, 97(6):1717-1737. |
| [11] | Simiu Emil, Scanlan Robert H. Wind effects on structures fundamentals and applications to design[M]. 3rd ed. NewYork:A Wiley-Inter science Publication, 1996. |
| [12] | Wilde K, Fujino Y, Masukawa J. Time domain modeling of bridge deck flutter[J]. Structural Engineering Earthquake Engineering, 1996, 13(2):93-104. |
| [13] | 邵亚会, 葛耀君, 柯世堂. 超大跨度悬索桥二维颤振频域直接分析方法[J]. 哈尔滨工业大学学报, 2011, 43(8):119-123. Shao Yahui, Ge Yaojun, Ke Shitang. Straight forward method for two-dimensional flutter analysis of super-long-span suspension bridge in frequency domain[J]. Journal of Harbin Institute of Technology, 2011, 43(8):119-123. |



