2. 中国人民解放军 94710部队, 江苏无锡 214142;
3. 中国人民解放军 93256部队, 沈阳 110043;
4. 空军航空大学, 安徽蚌埠 233000
2. Chinese People's Liberation Army with Number of 94710, Wuxi Jiangsu 214142, China;
3. Chinese People's Liberation Army with Number of 93256, Shenyang 110043, China;
4. Air Force Aeronautical University, Bengbu Anhui 233000, China
脉冲爆震发动机(PDE)具有很高的循环热效率、结构简单、推重比高[1, 2],因此,在过去的几十年中得到了广泛而深入的研究[3, 4, 5, 6, 7, 8]。即便如此,PDE的若干瓶颈问题至今仍未得到很好的解决。为解决高频起爆的问题,2001年,Levin[9]提出了一种新概念PDE,称之为2-Stage PDE。随后,美国、日本和中国也先后开展了相关研究。美国GE研究中心[10, 11]分别于2003和2005年对2-Stage PDE进行了冷、热态实验。结果表明,冷态条件下二维凹面腔中气流流动表现出高频自振荡的特性,在特定压力下振荡幅值较大;热态试验获得了1200Hz,压力振幅超过15%环境压力的脉动燃烧,但没有出现高频爆震。2008年,南京航空航天大学[12]通过连续的二维超声速射流对撞得到了间断产生的激波,研究了压比对激波频率与幅值的影响规律,并进行了初步的热态试验,但没有产生爆震燃烧。2013年,据俄罗斯“新闻新空网”报道,俄罗斯留里卡设计局设计了一种2-Stage PDE样机并进行了长达10min的试验,结果表明,发动机的平均推力超过100kg,比推力和燃油效率比常规的喷气发动机提高了30%~50%。
目前,国内外对2-Stage PDE的研究报道多为整机试验研究,原理性基础研究较少。事实上,2-Stage PDE的工作过程十分复杂,涉及一级预燃、超声速射流聚心碰撞诱导非定常激波、激波聚焦及起爆爆震等一系列复杂的物理化学过程,并具有高瞬态性、对几何结构和气动热力学参数敏感等特点。因此,对其工作循环中的各物理过程进行单独的简化研究,有助于掌握2-stage PDE各环节的工作机理及关键技术。因此,利用暂冲式激波管或类激波管装置针对2-Stage PDE工作过程中非定常激波在凹面腔内聚焦及起爆爆震波这一重要环节进行机理性实验十分必要。但目前来看,大部分暂冲式激波聚焦实验都是在二维凹面腔中进行的[13, 14, 15],关于此过程的流场演化及细节特征已有较多的研究成果。然而,研究表明,二维凹面腔与三维凹面腔中的激波聚焦存在着较大区别[16],而关于后者的实验研究更是鲜有报道。
本文设计了三维暂冲式激波聚焦及起爆实验装置,分别以空气和C2H2/Air混合气为介质,开展了暂冲式激波聚焦与起爆爆震实验。测得了激波聚焦时刻凹面腔底部的动态压力曲线,并在热态实验中获得了爆震波。同时,对实验中的工况进行了高精度的数值模拟,揭示激波聚焦及起爆爆震波的机理,为2-Stage PDE原理样机的设计提供技术基础。
1 实验装置与计算方法 1.1 实验装置暂冲式激波聚焦及起爆爆震实验系统原理图及照片如图 1、2所示。整个实验系统由高压段、双膜机构、实验段、喷口罩和测速管5部分构成。高压段用于储存实验所需的压缩空气或燃料/空气混合气。在高压段下游设置2个充气接口,其中一个通过单向阀与空压机相连,用于充入压缩空气;另一个通过单向阀与燃料掺混罐相连,用于填充混合气。空压机、燃料掺混罐和针形截止阀均通过耐压管与充气接口相连。高压段既可只填充压缩空气作为驱动段,又可充入空气/燃料混合气作为驱动气体。此处,双膜机构确保了入射激波强度在相同工况下具有很好的重复性。

|
| 图 1 暂冲式激波聚焦起爆实验系统示意图 Fig. 1 Schematic of blowndown shock focus apparatus |

|
| 图 2 暂冲式激波聚焦起爆实验系统照片 Fig. 2 Photo of blowndown shock focus apparatus |
实验段由壳体、喷口罩、锥形整流罩和凹面腔单元组成,如图 3所示。凹面腔单元由凹面腔、锥形整流罩和4个翼型支板构成,其中,凹面腔的型面曲线为x3+y3+z3=37.753,x=-16.5mm的部分球面。凹面腔与锥形整流罩通过周向均布的8个沉头螺钉连接,实验时用螺钉罩将8个螺钉的沉孔盖住,以保证壁面的光滑度。压电式压力传感器(美国Dytran公司的2300V5压电式动态压力传感器,测量范围为0~5000psi,谐振频率500kHz)从整流锥内部旋入凹面腔底部的螺纹孔,电缆从其中一块翼型支板引出,与测试电路相连。

|
| 图 3 实验段照片 Fig. 3 Photos of test section |
为测量燃烧后激波与火焰的传播速度,以验证是否为爆震燃烧,设计了测速管,如图 4所示。沿测速管轴向间隔0.1m均匀布置了8个火焰离子探针,它们各自的输出信号经信号调理电路综合成一路输出。在前4个火焰离子探针所在横截面与离子探针成90°角的轴向上布置4个动态压力传感器。测速管上游通过法兰与喷口罩相连,故整个低压段(测速管和实验段)都是连通的。在测速管上游设置一个与真空泵相连的抽气孔,用于将整个低压段抽真空。在测速管下游末端,通过将爆破膜片夹在2个法兰之间将整个低压段密封。

|
| 图 4 测速管照片 Fig. 4 Photo of velocity test section |
为揭示环形喷口宽度和驱动压力对激波聚焦影响的作用机理,采用与实验段1:1的二维轴对称模型进行了数值模拟研究。由于激波在凹面腔内聚焦的波系结构复杂,且具有高瞬态性,故进行了简化处理,忽略了体积力、气体粘性和传热的影响。为节省计算资源,网格划分采用块结构网格自适应加密算法,根据设定的密度梯度来标记需要加密的区域。在保持整个实验段与实际尺寸1:1的同时,缩短了高压段的长度,以减少计算量。在冷态模拟中,采用三阶龙格-库塔格式对时间进行离散,三阶WENO格式对空间进行离散,来求解非定常的Euler方程。为了与热态实验进行对比,热态模拟中采用了C2H2/O2/N2的单步反应机理,化学反应速率和气体的物理性质通过Chemkin库计算得到。并利用MUSCL-Roe/HLL混合算法及半隐式的龙格-库塔算法求解带化学反应的多组分欧拉方程。计算模型及根据密度梯度标记的3层待加密(2×2×4)区域如图 5所示。初始网格尺寸为0.2mm,加密后的最小网格尺寸为0.0125mm,如图 6所示。
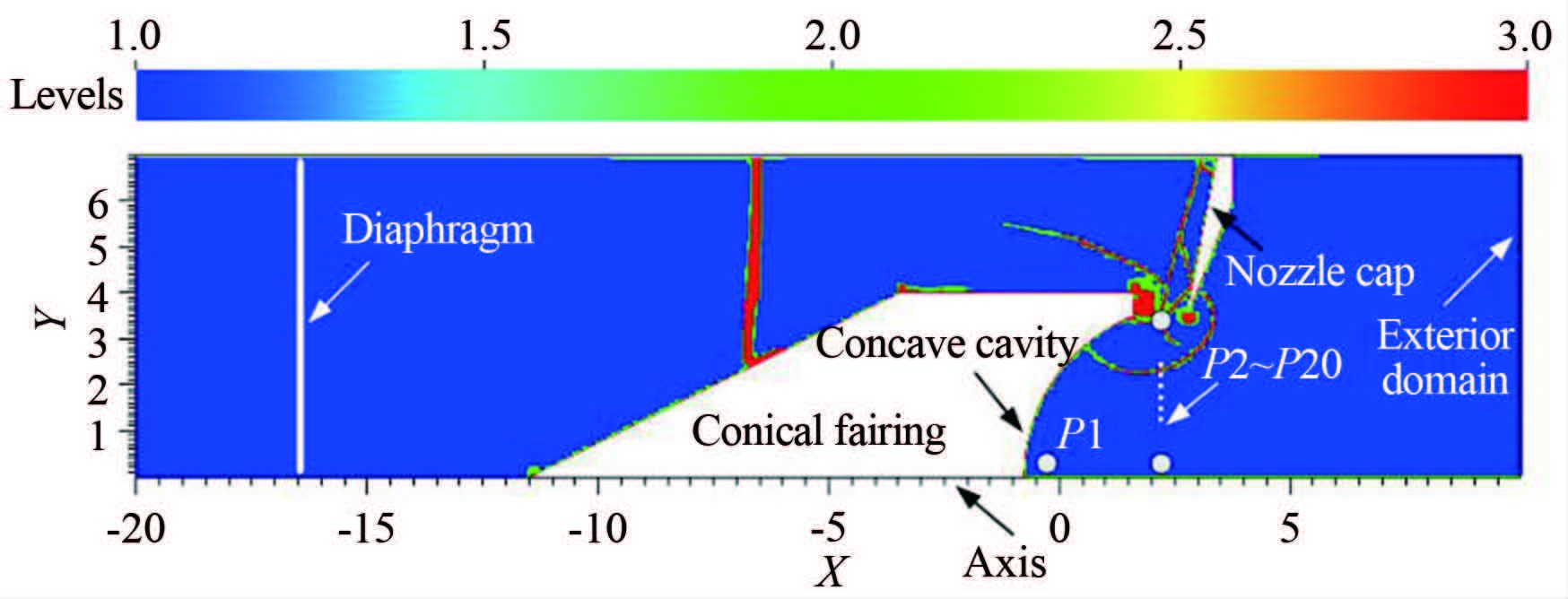
|
| 图 5 部分计算区域及根据密度梯度标记的待加密区域 Fig. 5 Computational model and AMR levels |

|
| 图 6 初始网格与经过2×2×4三层加密后的网格划分 Fig. 6 Initial and 2×2×4 refined grids |
从锥形整流罩之前40mm处到上游末端壁面之间为高压区,将该区域的温度和压力分别初始化为300K和0.55MPa。凹面腔壁面为半圆(x2+y2=37.752,x=-16.5mm)绕对称轴y=0旋转而成。环形喷口宽度d=5.4mm,计算外区向下游延伸10倍凹面腔深度的距离(由于计算区域过大,图 5只截取了关键区域)。为定量分析流场特征,在凹面腔底部顶点处设置了一个监测点P1,环形射流对撞面的中线上设置了19个监测点,如图 5所示。所有壁面均为等温壁面,温度恒定为Twall=300K;外区域出口为压力出口边界,pout=0.091MPa,温度Tout=300K。
1.3 数值算法验证图 7(a)、(b)是文献[14]中激波聚焦前后的阴影照片。7(c)、(d)是利用本文的数值方法得到的数值纹影。需要说明的是,阴影与纹影方法虽有不同,但二者均是通过密度相关的函数来反映流场中波系结构的,故可进行定性的对比。数值模拟中捕捉到了反射激波R、原过渡规则反射的滑移线S、壁面激波W以及主反射激波M,与实验结果吻合的较好。通过以上对比可以说明,本文采用的数值模拟方法合理,具有较高的可信度。
为验证数值算法模拟激波聚焦起爆过程的可靠性,在与文献[17]条件相同的条件下进行了激波聚焦起爆爆震波的数值计算,实验和数值计算结果对比见图 8。从图中可见数值结果中激波和爆震波结构与实验结果非常吻合。数值计算结果中的爆震波的不稳定结构和得到的爆震波速度等与实验结果较为吻合。证实了MUSCL-Roe/HLL 算法计算结果与实验基本相同,且具有较高的分辨率,能够捕捉到细微的流场结构。
在环形喷口宽度d=5.4mm,驱动压力pres=0.55MPa,初始压力pinit=0.091MPa的条件下,进行了暂冲式激波聚焦冷态实验。图 9(a)为实验测得的凹面腔底部的动态压力pbot和高压段内的驱动压力pres随时间的变化曲线。可以发现,凹面腔底部顶点处出现了多次压力峰值,相邻峰值的平均时间间隔为9.5ms。其中,第1次压力峰值为2.17MPa,为初始压力的23.8倍,是入射激波在凹面腔底部聚焦所致,而后续的压力峰值依次降低。
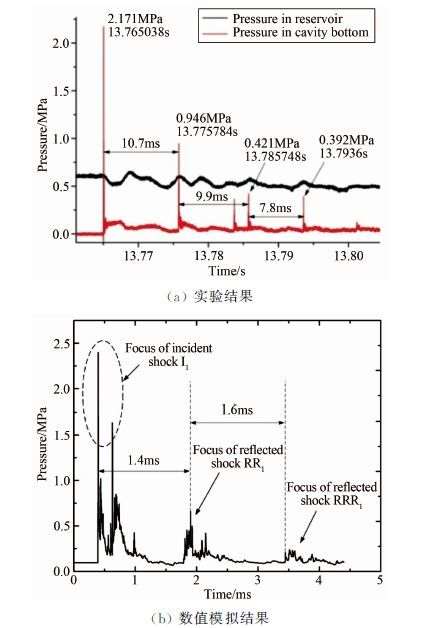
|
| 图 9 d=5.4mm凹面腔底部顶点处的压力时序 Fig. 9 Pressure history at cavity bottom,d=5.4mm ((a): experimental results; (b): numerical results) |
为揭示凹面腔底部的动态压力pbot形成多次峰值的原因,进行了高精度数值模拟。因计算资源所限,在实验段保持与实际尺寸1:1的前提下,将高压段缩减为0.1m,计算模型总长0.24m。图 9(b)为数值模拟中凹面腔底部监测点的压力时序。可见,第1次压力峰值为2.39MPa,与实验值相差10%;计算中,相邻2次激波聚焦的时间间隔平均为1.5ms,而实验装置的实际总长为1.6m,为计算模型长度的6.67倍。按此比例估算,实验中测得相邻2次激波聚焦的时间间隔应为1.5×6.67,约10ms,与实验结果相差5%。误差主要来源于计算中求解的是Euler方程,忽略了粘性、热传导等因素。此外,由于实验中的凹面腔底部顶点处布置的动态压力传感器一方面不可避免地破坏了凹面腔的型面,另一方面,传感器的安装位置也无法确保与数值模拟中监测点的位置完全一致。况且在激波聚焦时刻,凹面腔底部的压力梯度极大。故计算值较实验值略有偏差。
图 10(a)~(d)为第1次激波聚焦的流场演化数值纹影图。在t=275.57μs时刻(见图 10(a)),入射激波I1到达喷口罩前,并向凹面腔内部衍射。在锥形整流罩的中间有一道接触间断D1,将膨胀波后的气流与入射激波之后的气流分开。到了t=343.513μs时刻(见图 10(b)),入射激波I1在对称轴上聚心碰撞,同时,入射激波I1被喷口罩完全反射,形成反射激波R1。随后,第一次激波聚焦发生在t=397.374μs时刻(见图 10(c)),此时,反射激波R1继续向高压段方向传播。到了t=728.236μs时刻(见图 10(d)),反射激波R1已反传至上游通道锥形整流罩的中部。
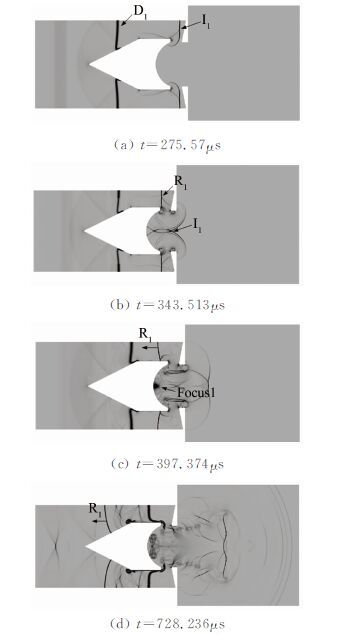
|
| 图 10 第一次激波聚焦的流场演化数值纹影 Fig. 10 Numerical schlieren of flow field development during the first shock focus |
如图 11(a)所示,反射激波R1在t=1065.13μs时刻到达高压段末端,在壁面发生反射,形成反射激波RR1(Re-reflected wave),之后,再次作为入射激波I2向下游传播(见图 11(b)~(d))。在t=1743.67μs时刻,入射激波I2到达喷口罩,形成反射激波R2,同时向凹面腔内衍射。到了t=1799.3μs时刻,入射激波I2在凹面腔底部聚焦,形成第二次激波聚焦。同时,反射激波R2继续向环形通道上游回传。
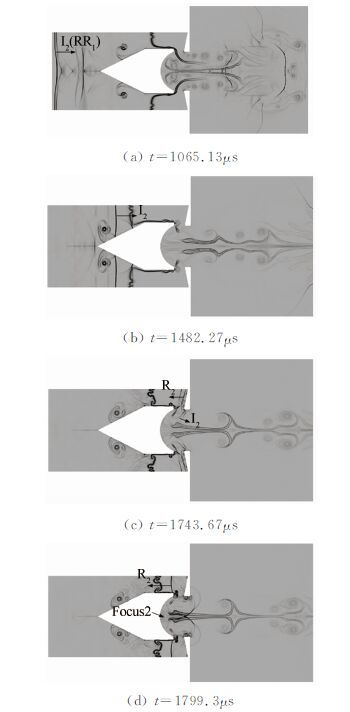
|
| 图 11 第二次激波聚焦的流场演化数值纹影 Fig. 11 Numerical schlieren of flow field development during the second shock focus |
反射激波R2继续向高压段传播(见图 12(a)、(b)),与前述情况相同,在遇到高压段末端壁面后反射,形成反射激波RRR1(Re-re-reflected wave),如图 12(c)所示,其作为下一阶段的入射激波I3向下游传播。在t=3439.17μs时刻,入射激波I3在凹面腔底部聚焦,形成第3次激波聚焦,如图 12(d)所示。
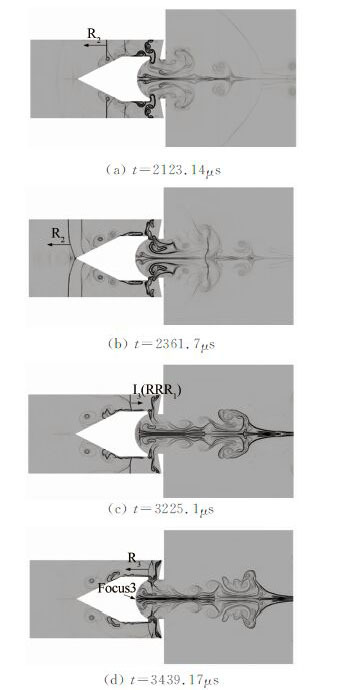
|
| 图 12 第三次激波聚焦的流场演化(数值纹影) Fig. 12 Numerical schlieren of flow field development during the third shock focus |
由此可见,图 9(b)(凹面腔底部顶点处监测点的压力时序)中形成的3次压力峰值分别为入射激波I1聚焦、反射激波RR1(入射激波I2)聚焦和反射激波RRR1(入射激波I3)聚焦所致。由于入射激波在多次反射过程中与接触间断、涡等多次作用,强度渐弱,后续的几次激波聚焦强度也依次减弱。
2.2 冷态实验的数值模拟分析 2.2.1 入射激波的衍射及诱导射流的发展对于入射激波在变截面管道中的传播行为,Skews[18]已通过实验和数值模拟系统地进行了描述。因此,本文仅对入射激波衍射,进入凹面腔之后的行为进行描述。如图 13(a)所示,在t=253.225μs时刻,衍射激波作为入射激波已完全进入凹面腔,称之为入射激波I1。此时的原入射激波已在喷口罩完全反射,形成的反射激波在向上游运动的同时也向凹面腔内衍射,形成了入射激波I2。入射激波I2与前导的入射激波I1像齿轮一样从右至左依次咬合,如图 13(b)~(d)所示。

|
| 图 13 入射激波衍射过程的数值纹影图 Fig. 13 Numerical schlieren during the diffraction of incident shocks |
如图 13(b)所示,在t=256.692μs时刻,向上游回传的反射激波到达涡流区,与涡发生相干。从图 13(b)中的数值纹影放大图可见,除反射激波之外,并无其它次生激波存在,反射激波被涡分割为3段,呈“S”状,中间一段几乎横贯涡核,为典型的弱相干。
随着入射激波后射流的进一步发展,在t=261.542μs时刻,涡强度增强,其与激波的相干转变为强相干[19],反射类型为马赫反射,如图 13(c)所示。从喷口罩上反射的激波,其上半部分作为入射激波I1继续向环形通道上游运动,与涡的上半部分相互作用,产生了弯曲的马赫干M2,反射激波R2和滑移线S2。同样的,反射激波的下半部分在环形喷口的左侧壁面上再次反射后,一方面向右侧运动,与涡的下半部分相互作用,产生了马赫干M1,反射激波R1和滑移线S1;另一方面,向凹面腔内衍射,形成了入射激波I3。同样的,入射激波I3也从入射激波I2的一侧逐渐与之融合。
随着流场的进一步发展,在t=290.444μs时刻,入射激波I1与入射激波I2的大部分已经融合,它们在壁面的反射类型为马赫反射,尽管马赫干在数值纹影中较难分辨,但从图 13(d)的局部放大区域B中可见,由于入射激波在运动过程中不断受到凹面的压缩,反射点产生的压缩波将入射激波向下游推动,使入射激波的根部明显向下游凸起。同时,从区域A可见,此时入射激波I3在凹面腔内壁的反射类型为规则反射。在入射激波I3与入射激波I1、I2之间为若干道衍射激波退化成的压缩波。此时,环形喷口的出口处形成了明显的二次激波,在二次激波靠近凹面腔的一侧,出现了1个明显的涡,且有再压缩激波的存在。同时,环形喷口右侧滑移线的彻底失稳及破碎涡的出现,都表明射流已经得到了充分发展。
如图 14所示,在t=312.278μs时刻,入射激波I2已经追上入射激波I1,并完全叠加在一起。入射激波I1、I2与入射激波I3之间的压缩波系也彼此靠近,有逐渐合并的趋势。沿着图 14(a)中的有向线段L1提取了沿程100个采样点的密度值,作出的曲线如图 14(b)所示。从图 14(b)中的曲线可见,起初,气流密度在环形喷口出口处的膨胀波扇作用下急剧减小,此区域对应着图 14(a)中的I区。在a点,密度值出现一个较小的跃升,对应着图 14(a)中的斜激波。随后在b点,气流密度出现了一个大幅度的跳变,这是由于穿越了二次激波。在二次激波下游与入射激波I3之间为压缩波区,对应着曲线中的II区和III区。很明显,压缩波导致的密度增大不同于穿越激波时的跳变,而是在波动中缓慢增大。在压缩波区的某个位置c处,密度值达到最大,随后又缓慢下降。在d点处,气流密度有一个明显的下降,对应图 14(a)中的入射激波I3。紧接着,气流密度在e点处又出现了一次下降,对应着入射激波I3与入射激波I1、I2之间的压缩波。此后,在f点处密度值再次出现陡降,这是由于穿越了叠加在一起的入射激波I1、I2。
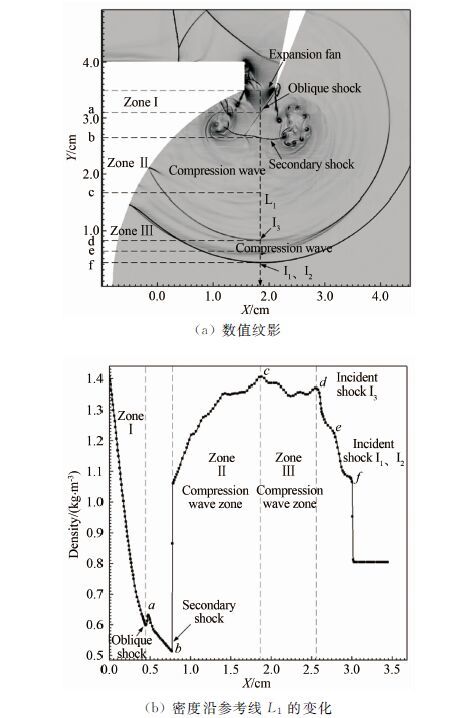
|
| 图 14 t=312.278μs时刻的数值纹影和密度沿参考线L1的分布 Fig. 14 Numerical schlieren and density distribution along L1 at t=312.278μs |
在t=319.804μs时刻,前导的入射激波I1、I2已经接近凹面腔的对称轴,即将发生聚心碰撞。此时,从环形喷口喷出的射流已经充分发展,射流边界(滑移线)进一步失稳,“S”型链状的K-H不稳定结构破碎成多个涡(见图 15)。注意到,靠近凹面腔一侧的涡在涡核与壁面之间诱导出逆向的超声速区,从而出现了一道再压缩激波。沿着有向线段L1提取50个采样点的速度值,作出的曲线如图 16所示。气流经过再压缩激波后,速度值从360m/s陡降至135m/s,以便进一步调整方向,形成涡流。

|
| 图 15 t=319.804μs时刻的数值纹影 Fig. 15 Numerical schlieren at t=319.804μs |
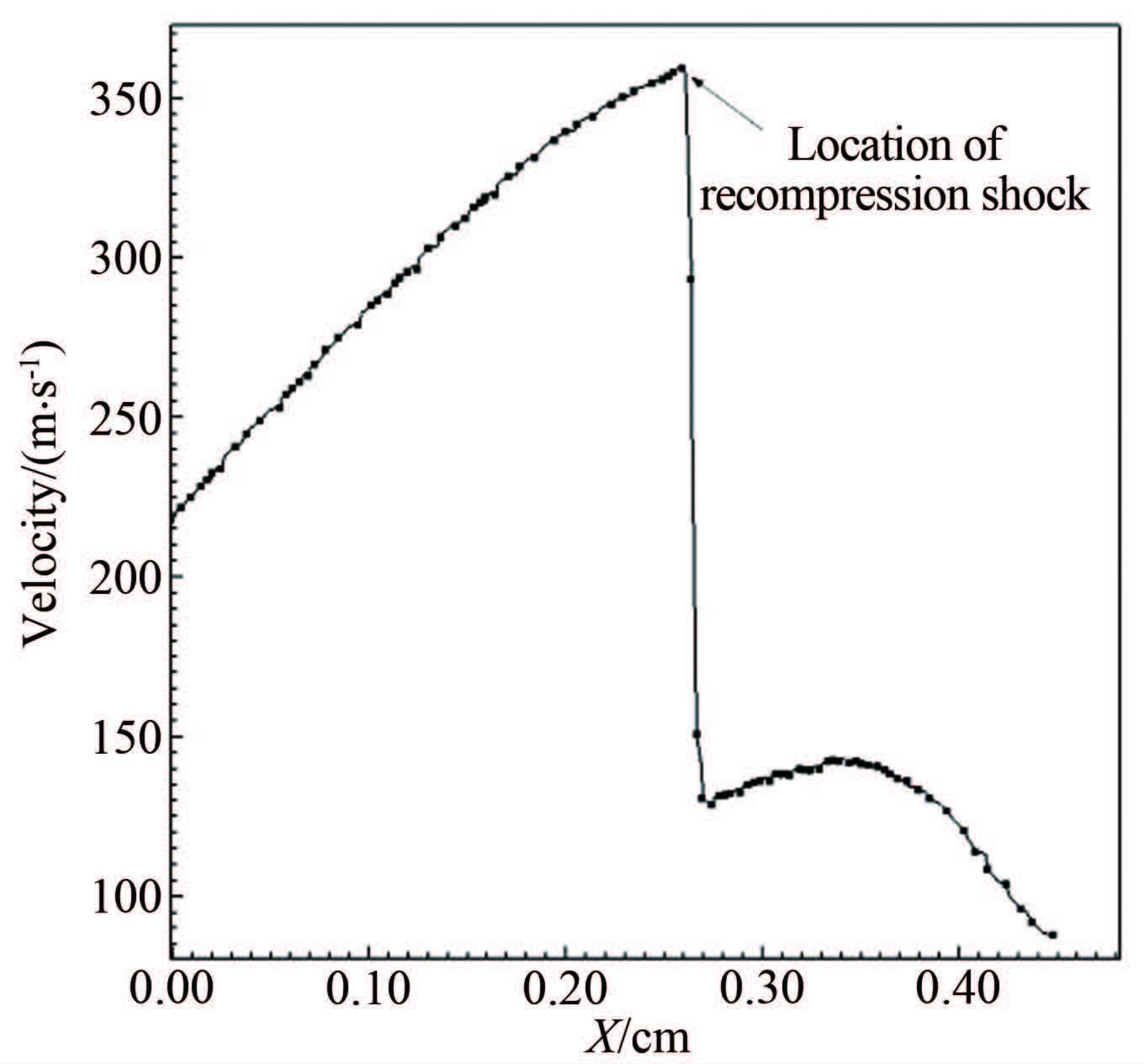
|
| 图 16 速度沿图 15中参考线L1的变化 Fig. 16 Velocity distribution along L1 in Fig 15 |
如图 17(a)~(c)所示,入射激波I1、I2首先在对称轴上聚心碰撞。紧接着,在t=322.33μs时刻,入射激波I1、I2与入射激波I3之间的压缩波也在对称轴上聚心碰撞,随着流场的进一步发展,在t=326.008μs时刻,入射激波I3也到达对称轴并发生碰撞。

|
| 图 17 衍射激波聚心碰撞过程中流场演化的数值纹影 Fig. 17 Numerical schlieren during implosion of diffracted shock |
如前所述,入射激波I1、I2,压缩波和入射激波I3先后在对称轴上聚心碰撞,形成了3层椭球形激波阵面,在t=333.505μs时刻,前2层合并为椭球形激波E1,如图 18所示。此时,由入射激波I3聚心碰撞形成的椭球形激波E2距离椭球形激波E1的左端点尚有一段距离。从图 18的局部放大区域A可见,椭球形激波的左端面实质上是两个沿对称轴对称分布的马赫反射结构,入射激波I、反射激波R、马赫干M、三波点T和滑移线S均清晰可见,上下2个马赫反射结构共同拥有1个马赫干。注意到,此时的入射激波I3在壁面的反射类型仍然维持着von Neumann型过渡规则反射。1994年,Izumi[20]在系统地研究轴向入射的激波聚焦时认为,沿对称面对称分布的上下2个马赫干的碰撞标志着激波聚焦的完成。不同的是,本文中的入射激波是沿凹面腔径向入射的,首先发生的入射激波聚心碰撞形成了沿对称轴对称分布的马赫反射结构,马赫干作为入射激波向凹面腔底部推进,同时,原入射激波也向凹面腔底部运动。因此,激波聚焦是由原入射激波和新形成的马赫干共同参与完成的。

|
| 图 18 t=333.505μs时刻的数值纹影 Fig. 18 Numerical schlieren at t=333.505μs |
如图 19所示,在t=335.038μs时刻,入射激波I1、I2和马赫干同时在凹面腔底部碰撞,激波聚焦得以完成。形成的反射激波刚刚从对称轴上分开,并出现了2个马赫反射结构,如图 19中的局部放大区域A。2个马赫反射结构的滑移线相交于对称轴上,形成了1个朝向凹面腔底部的射流J1。从图 19中的局部放大区域B可以清晰地观察到椭球形激波的右侧部分与左侧相同,也是2个马赫反射结构,且椭球形激波E2在不断地靠近椭球形激波E1。

|
| 图 19 t=335.038μs时刻的数值纹影 Fig. 19 Numerical schlieren at t=335.038μs |
图 20(a)~(h)是激波聚焦后流场演化过程的数值纹影。从各图中的局部放大区域A可见,激波聚焦形成了较强的反射激波,为方便描述,称之为聚焦反射激波。聚焦反射激波为典型的马赫反射结构,如图 20(a)所示。从图 20(a)~(g)可见,聚焦反射激波的三波点始终朝向壁面运动,直至与壁面碰撞而消失。同时,马赫干逐渐变短,到t=361.815μs时刻(见图 20(g))已无法分辨,反射结构由反转马赫反射(InMR)转变为规则反射(RR)。在此过程中,沿对称轴对称分布的反射激波R不断变长并连接起来,形成一个气泡状的主反射激波,如图 20(g)所示。

|
| 图 20 激波聚焦后流场的数值纹影 Fig. 20 Numerical schlieren of post focus flow field |
在凹面腔底部顶点附近,聚焦反射激波的滑移线S与聚焦前椭球形激波E1滞留的滑移线S'相交于一点,形成了1个呈蘑菇状的朝向凹面腔底部顶点的射流J1(图 20(a))。随着流场的发展,射流J1向反方向卷曲,形成了上、下对称的2个涡V,如图 20(b)所示。同时,聚焦反射激波的滑移线S顺着射流向凹面腔底部滑动,使椭球形激波E1的滑移线出现了一个“S”状的扭结,呈现出K-H不稳定结构(KHI)的雏形,并最终导致滑移线的完全失稳(图 20(h))。从图 20(a)~图 (h)可见,“S”状扭结随着聚焦反射激波的滑移线S一起向凹面腔底部滑动,最终与对称轴上下的2个涡V一起在凹面腔底部壁面上发生碰撞。至此,滑移线完全失稳,形成了“S”型铰链状的K-H不稳定结构,如图 20(g)、图 (h)所示。
在椭球形激波的右端面,椭球形激波E2不断加速靠近椭球形激波E1,如图 20(a)~图 (e)所示。在t=342.943μs时刻,椭球形激波E2追上椭球形激波E1,它们的滑移线S"和S'相交在一起,也形成一个扭结,如图 20(e)所示。随着滑移线S"和S'进一步的相互作用,出现了一个新的与J1方向相反的射流J2,射流J2比J1弱,且朝向凹面腔的出口方向,如图 20(g)所示。
2.3 热态实验结果分析将实验中测得的凹面腔底部顶点压力与测速管上1#~4#压力传感器及火焰离子探针信号绘成曲线并按时空分布排列,如图 21所示。图中左侧纵轴为动态压力的度量标尺,每一大格代表 2MPa;右侧纵轴为离子探针输出的电压信号的度量标尺,每一大格代表 5V。可见,在t=9.5ms时刻,破膜产生的入射激波在凹面腔底部顶点附近聚焦,压力高达9.8MPa,且压力峰值出现较大振荡。此外,8个火焰离子探针都测到信号。根据文献[2],初始压力为0.1MPa、当量比为1.0的乙炔/空气混合气的C-J爆震波波后压力为1.9MPa。因此,初步判断激波聚焦触发了过驱爆震。
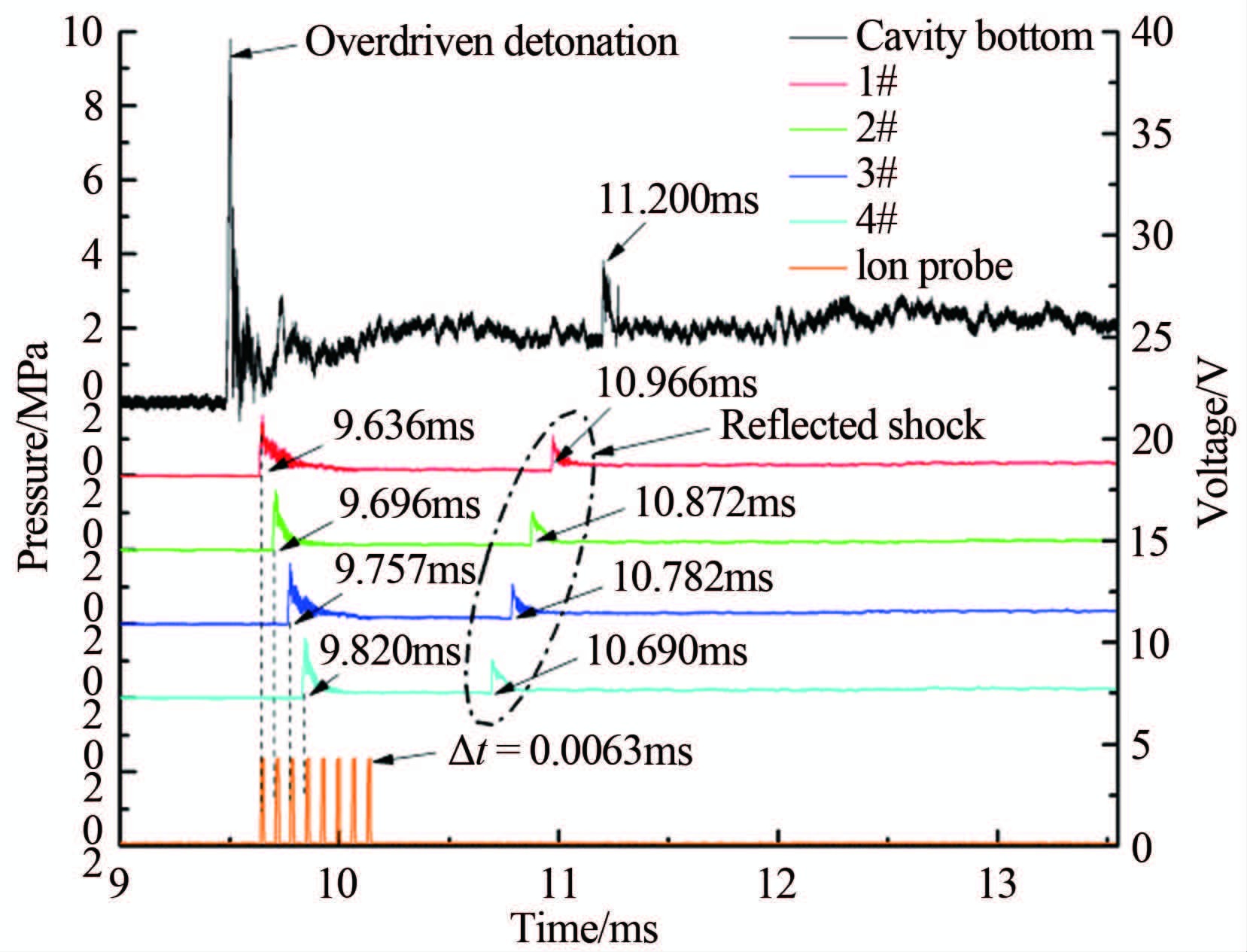
|
| 图 21 驱动压力为1.51MPa、加装测速管条件下凹面腔底部顶点压力与测速管上1#~4#压力传感器及火焰离子探针信号时空分布图 Fig. 21 Traces of 1#~4# PCB pressure sensor at cavity bottom and ion probe (pres=1.51MPa) |
此后,爆震波继续向测速管内传播,并依次扫过1#~4#动态压力传感器,对应着图中的1#~4#曲线。在t=9.636ms时刻,爆震波到达测速管内的1#传感器,峰值压力1.62MPa,接近于C-J爆震的波后压力[2]。紧接着,在t=9.696、9.757和9.820ms时,爆震波依次扫过2#、3#和4#动态压力传感器,据此可得出爆震波的平均传播速度为1631.1m/s。爆震波在到达测速管出口处时膜片破裂,同时形成的反射激波向测速管上游回传,又分别于t=10.69、10.782、10.872和10.966ms时刻先后经过4#、3#、2#和1#压力传感器。此外,从腔底的动态压力曲线可以看出,在爆震波起爆1.702ms之后,即t=11.2ms时刻,又出现一个约3.8MPa的压力峰值。此峰值是在反射激波到达1#压力传感器之后出现的,应为反射激波回传到凹面腔中所致。
从图 21中还可以发现,在t=9.64ms时刻,1#离子探针首先感受到了火焰离子信号,随后,火焰锋面先后到达2#~8#离子探针。8个离子探针是沿测速管轴线间隔0.1m均布的,读出的相邻方波间的平均时间间隔为0.063ms,据此可得爆震波的平均传播速度为1587.3m/s,火焰传播速度与激波传播速度之间的耦合偏差为2.7%。在5%的工程允许误差范围之内,可以认为激波阵面与火焰锋面是紧密耦合的。同时由文献[2]的附录2可以查得,初始压力为0.1MPa、当量比为1.0的乙炔/空气混合气的C-J爆震波传播速度为1866.6 m/s,实验测得速度为1587.3 m/s,达到了C-J爆震波速的85.1%。据此判断在此工况下成功起爆了爆震波。
2.4 热态实验的数值模拟图 22(a)~图 (d)是入射激波衍射、反射与聚焦过程的数值纹影。可以发现,此过程和冷态条件下的流场特征基本相同。需要说明的是,为减少计算量,将高、低压段的分界面设置在如图 22(a)中所示的位置,因此,接触面D将很快进入凹面腔(图 22(a)),并在反射激波的作用下发展为Richtmeyer-Meshkov不稳定结构,如图 22(b)所示。在图 22(c)中,入射激波I在凹面腔底部聚焦,RR-IR结构紧随其后。在图 22(d)中可以清晰地看到入射激波I聚焦后形成的反射激波F-R以及RR-IR结构在聚焦前的波系结构。
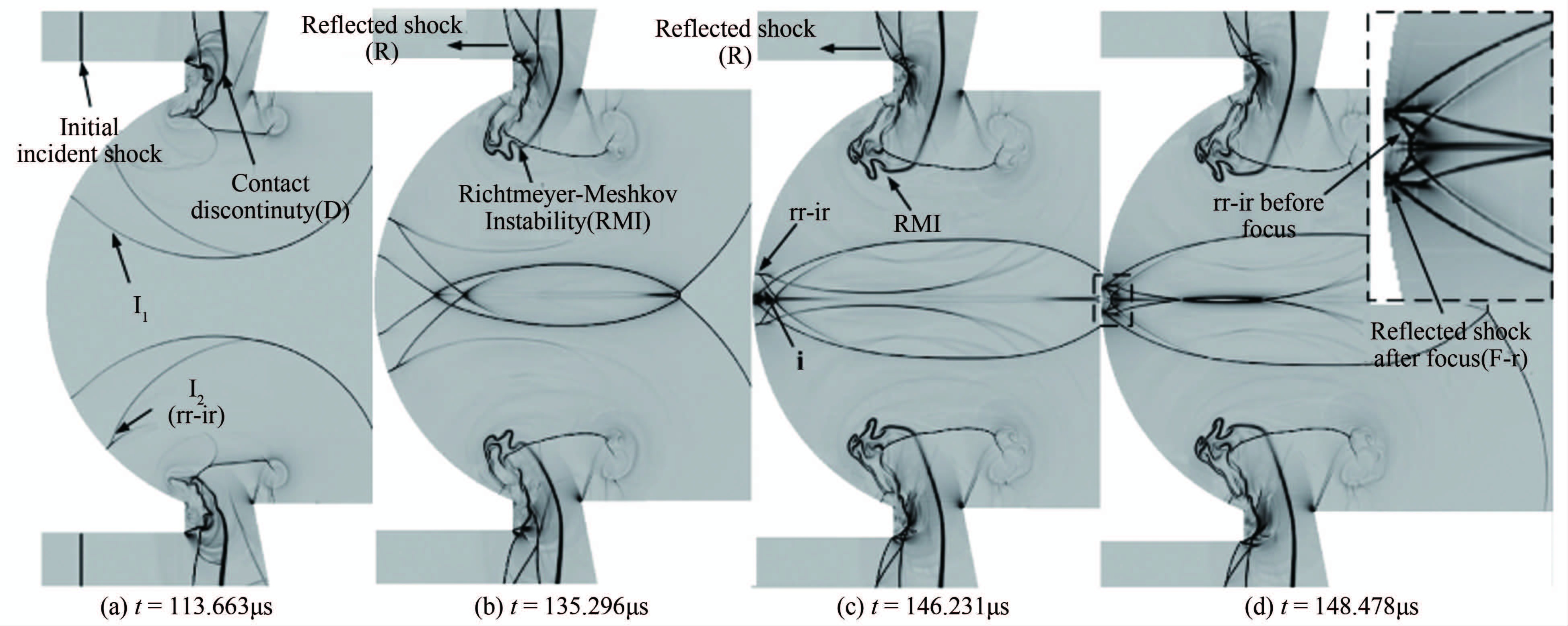
|
| 图 22 激波衍射、反射与聚焦过程的数值纹影 Fig. 22 Numerical schlieren during the processes of shock diffraction,reflection and focus |
RR-IR结构在t=150.198μs时刻在凹面腔底部完全反射,形成一个内凹的、自收缩的激波,如图 23(a)所示,这与SKEWS[14]观察到的轴向入射激波在聚焦时刻的行为极为相似。随后,在t=151.751μs时刻,自收缩的激波在对称轴上收缩成一条狭缝,至此,RR-IR结构完成聚焦,如图 23(b)所示。从局部放大区域A中的95%H2O浓度边界线可见,此时的激波与反应锋面是耦合在一起的,说明触发了爆震。此后,爆震波向凹面腔出口自持传播,如图 23(c)、图 (d)所示。

|
| 图 23 爆震触发过程的数值纹影 Fig. 23 Numerical schlieren during detonation onset |
图 24(a)~图 (d)是爆震波向凹面腔出口和环形喷口上游传播过程的数值纹影。可以发现,爆震波在通过环形喷口出口两侧的涡流区时,强度有所减弱,明显滞后于中轴线附近的爆震锋面,但其在传播和衍射的过程中始终没有熄爆。且在绕过环形喷口出口的拐角后,继续向环形喷口上游反传。
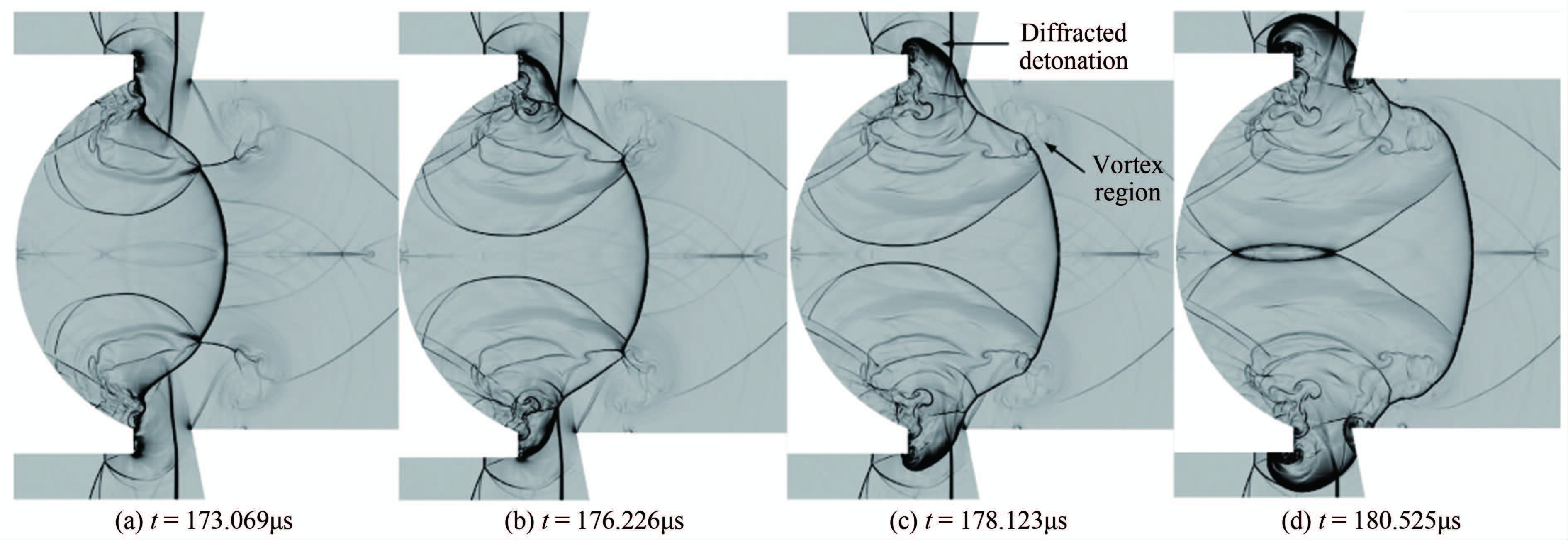
|
| 图 24 爆震传播及反传过程的数值纹影 Fig. 24 Numerical schlieren during the propagation and re-propagation of detonation |
图 25是爆震波起爆时刻的压力与温度云图。可见,激波聚焦点的压力与温度极高,分别达到18MPa和4000K。然而,正如前所述,聚焦点的空间尺度极小,且在环形喷口宽度d=11.4mm的工况下,由RR-IR结构产生的更强的聚焦点位于离开凹面腔底部顶点一定距离的对称轴上。因此,凹面腔底部顶点监测到的压力峰值要低得多(见图 26),仅为12.37MPa。可以发现,数值模拟结果比实验值的9.8MPa明显偏高。这是由于数值模拟中使用的是无粘模型,且没有考虑传热等损失的缘故。此后,过驱的爆震波在测速管内传播,压力与温度逐步下降,直至接近C-J爆震状态。

|
| 图 25 t=303.659μs爆震波起爆时刻的压力(a)和温度云图(b) Fig. 25 Contours of pressure(a) and temperature (b) when detonation is onset (t=303.659μs) |

|
| 图 26 凹面腔底部顶点处的压力时序 Fig. 26 Pressure history at cavity bottom (numerical results) |
图 27是监测点P1~P4的压力时序。图中第1个峰值为爆震锋面到达所致,后续更高的峰值则是由于爆震波在测速管壁面反射生成的马赫干到达以及反射激波到达所致。监测点的分布与热态实验中的实际工况一致,根据压力峰值的时间间隔得到的平均爆震波波速为2056m/s。而实验中测得的爆震波速为1587m/s,比数值模拟的结果明显偏低。这可能是由于在数值模拟中采用的是单步反应机理,且没有考虑粘性、传热等各种损失的缘故。
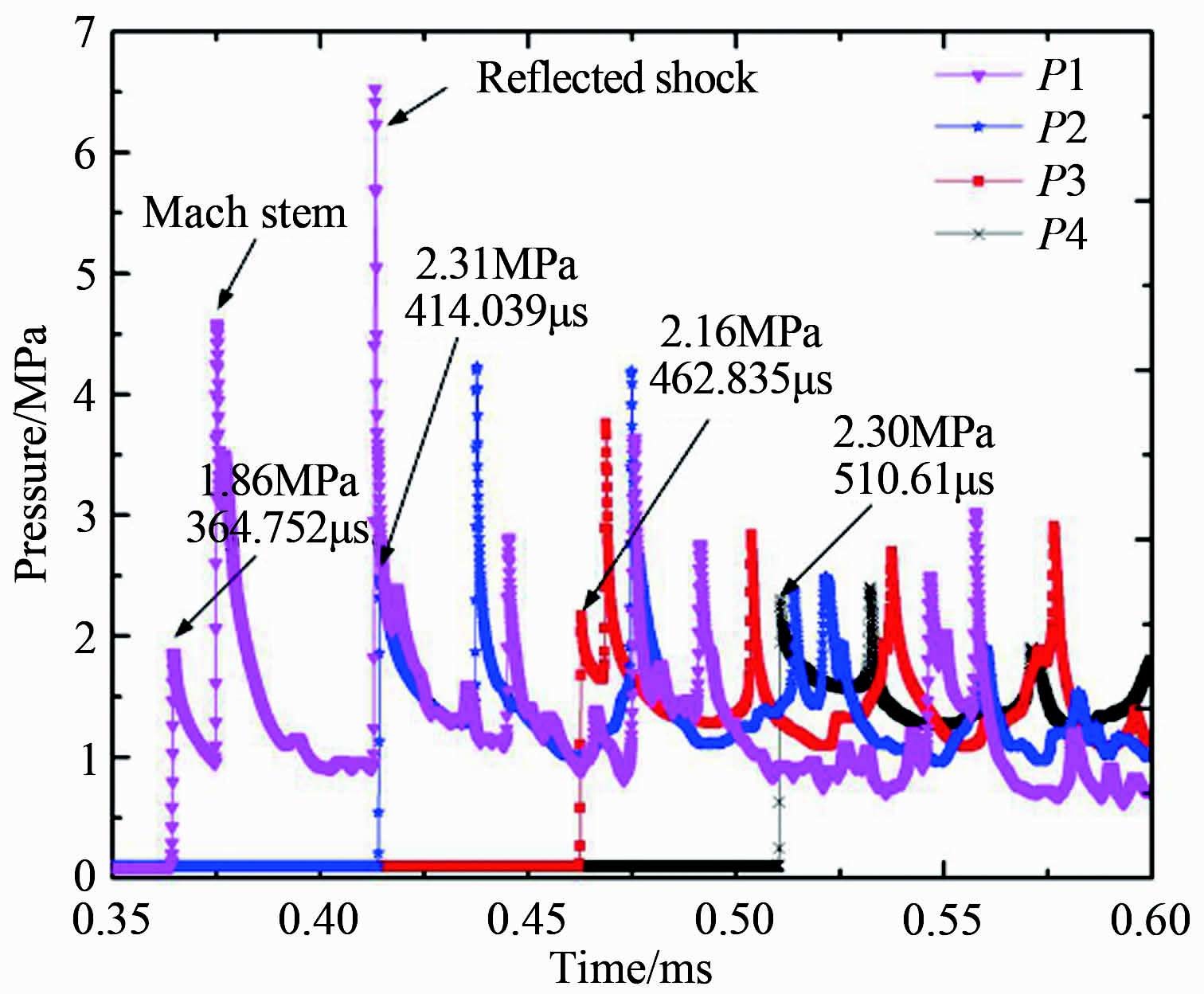
|
| 图 27 监测点P1~P4的压力时序 Fig. 27 Pressure history of P1~P4 (numerical results) |
通过三维暂冲式激波聚焦及起爆爆震的实验和数值模拟,得到了如下结论:
(1) 在环形喷口宽度d=5.4mm,驱动压力pres=0.55MPa,初始压力pinit=0.091MPa的条件下,凹面腔底部顶点处出现了多次压力峰值,相邻峰值的平均时间间隔为9.5ms。其中,第一次压力峰值为2.17MPa,为初始压力的23.8倍,是破膜产生的入射激波聚焦所致;后续的压力峰值依次降低,是破膜时产生的入射激波在喷口罩与高压段末端壁面之间多次反射,形成多次激波聚焦所致;
(2) 以当量比1.0的C2H2/Air混合气作为工质,在驱动压力为1.51MPa,环形喷口宽度d=11.4mm的工况下成功起爆了爆震波。测得火焰传播速度与激波传播速度之间的耦合偏差为2.7%,可认为激波阵面与火焰锋面紧密耦合;测得的爆震波传播速度为1587.3m/s,达到了C-J爆震波速的85.1%。由此验证了环形激波聚焦起爆爆震波的概念,为两级PDE的连续起爆奠定了理论基础;
(3) 环形激波沿三维凹面腔径向入射,首先在对称轴上聚心碰撞,形成沿对称轴对称分布的马赫干,并作为入射激波向凹面腔底部推进,原入射激波也同时向凹面腔底部运动。因此,环形激波沿三维凹面腔径向入射聚焦的完成是以原入射激波和新形成的马赫干在凹面腔底部碰撞为标志的。
| [1] | 严传俊, 王绍卿. 脉冲爆震发动机工作原理与循环分析[J]. 推进技术, 1996, 17(3):56-63. |
| [2] | 严传俊, 范玮, 郑龙席, 等. 脉冲爆震发动机原理及关键技术[M]. 西北工业大学出版社, 2005. |
| [3] | 严传俊, 范玮, 黄希桥, 等. 新概念脉冲爆震发动机的探索性研究[J]. 自然科学进展, 2002, 12(10):1021-1025. |
| [4] | 张群, 范玮, 徐华胜. 中国脉冲爆震发动机技术研究现状及分析[J]. 航空发动机, 2013, 39(3):18-22. Zhang Qun, Fan Wei, Xu Huasheng. A review on research status of pulse engines in China[J]. Aero-engine, 2013, 39(3):18-22. |
| [5] | 郑龙席, 卢杰, 严传俊, 等. 脉冲爆震涡轮发动机研究进展[J]. 航空动力学报, 2014, 29(5):993-1000. Zheng Longxi, Lu Jie, Yan Chuanjun, et al. Research progress on pulse detonation turbine engine[J]. Journal of Aerospace Power, 2014, 29(5):993-1000. |
| [6] | Roy G, Frolov S, Borisov A, et al. Pulse detonation propulsion:challenges, current status, and future perspective[J]. Progress in Energy and Combustion Science, 2004, 30(6):545-672. |
| [7] | Eidelman S, Grossmann W, Lottati I. A review of propulsion apllication of the ppulse detonation engine concept[J]. Journal of Propulsion and Power, 1991, 6:857-865. |
| [8] | 严传俊, 何立明, 范玮, 等.脉冲爆震发动机的研究与发展[J]. 航空动力学报, 2001, 16(3):212-217. Yan Chuanjun, He Liming, Fan Wei, et al. Research and development of pulse detonation engines[J]. Journal of Aerospace Power, 2001, 16(3):212-217. |
| [9] | Levin V A, Nechaev J N, Tarasov A I. A New Approach to Organizing Operation Cycles in Pulse Detonation Engines[C]. Moscow:High-Speed Deflagration and Detonation:Fundamentals and Control, 2001:223-238. |
| [10] | Ivett A Leyva, Venkat Tangirala. Investigation of Unsteady Flow Field in a 2-Stage PDE Resonator[C]. USA:41st Aerospace Sciences Meeting and Exhibit, 2003:715-723. |
| [11] | Keith R, McManus, Dean A J. Experimental Evaluation of a Two-Stage Pulse Detonation Combustor[R]. AIAA-2005-3773. |
| [12] | 周鸿. 两步法高频爆震发动机(Two-stage PDE)机理与特性研究[D]. 南京:南京航空航天大学, 2008. |
| [13] | Achasov O V, Panyazkov O G. Some Gasdynamic Methods for Control of Detonation Initiation and Propagation[C]. Moscow:High-Speed Deflagration and Detonation:Fundamentals and Control, 2001:31-44. |
| [14] | Skews B W, Kleine H. Flow features resulting from shock wave impact on a cylindrical cavity[J]. Journal of Fluid Mechanics, 2007, 580:481-493. |
| [15] | Skews B W, Kleine H. New Flow Features in a Cavity During Shock Wave Impact[C]. Crown Plaza:16th Australasian Fluid Mechanics Conference, 2007. |
| [16] | Liang S M, Wu L N, Hsu R L. Numerical investigation of axisymmetric shock wave focusing over paraboloidal reflectors[J]. Shock Waves, 1999, 9(6):367-379. |
| [17] | Gelfand B E, Khomik S V, Bartenev A M, et al. Detonation and deflagration initiation at the focusing of shock waves in combustible gaseous mixture[J]. Shock Waves, 2000, 10:197-204. |
| [18] | Dowse J, Skews B. Area change effects on shock wave propagation[J]. Shock Waves, 2014, 24:365-373. |
| [19] | Barik H, Chatterjee A. Existence criteria for reflection configurations in shock-vortex interactions[J]. Shock Waves, 2007,16:309-320. |
| [20] | Izumi K, Aso S, Nishida M. Experimental and Computational Studies Focusing Process of Shock Waves Reflected from Parabolic Reflectors[J]. Shock Waves,1994, 4(3):213-222. |





