2. 中国空气动力研究与发展中心, 四川绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
近30年来,以粒子图像测速技术(Particle Image Velocimetry,PIV)为代表的全流场非接触测量方法被广泛地应用于实验流场测量中。这类方法的原理是在流场中均匀地布撒示踪粒子,通过短时间间隔的2幅图片确定粒子的运动速度,并以此速度代表流体的运动速度,从而得到全流场的流动参数。自粒子图像测速技术诞生以来,凭借其多点同时测速的优势,已经发展成为流场测试的主流试验手段,并正在逐步取代2种最重要的逐点速度测量方法:热线风速测量法(Hot-Wire Anemometry,HWA)和激光多普勒速度测量法(Laser-Doppler Velocimetry,LDV)[1],广泛应用于各类流场信息的获取。从河道内水生植物跟湍流的相互作用[2]到超声速边界层中三维拟序结构的观察[3],乃至生物学界鸡胚心脏中血浆流速的测量[4],都有PIV技术的应用。近些年来,由于高能量激光器和短跨帧时间、高分辨率CCD相机的出现,使得PIV技术应用于超声速流场的测量成为可能。
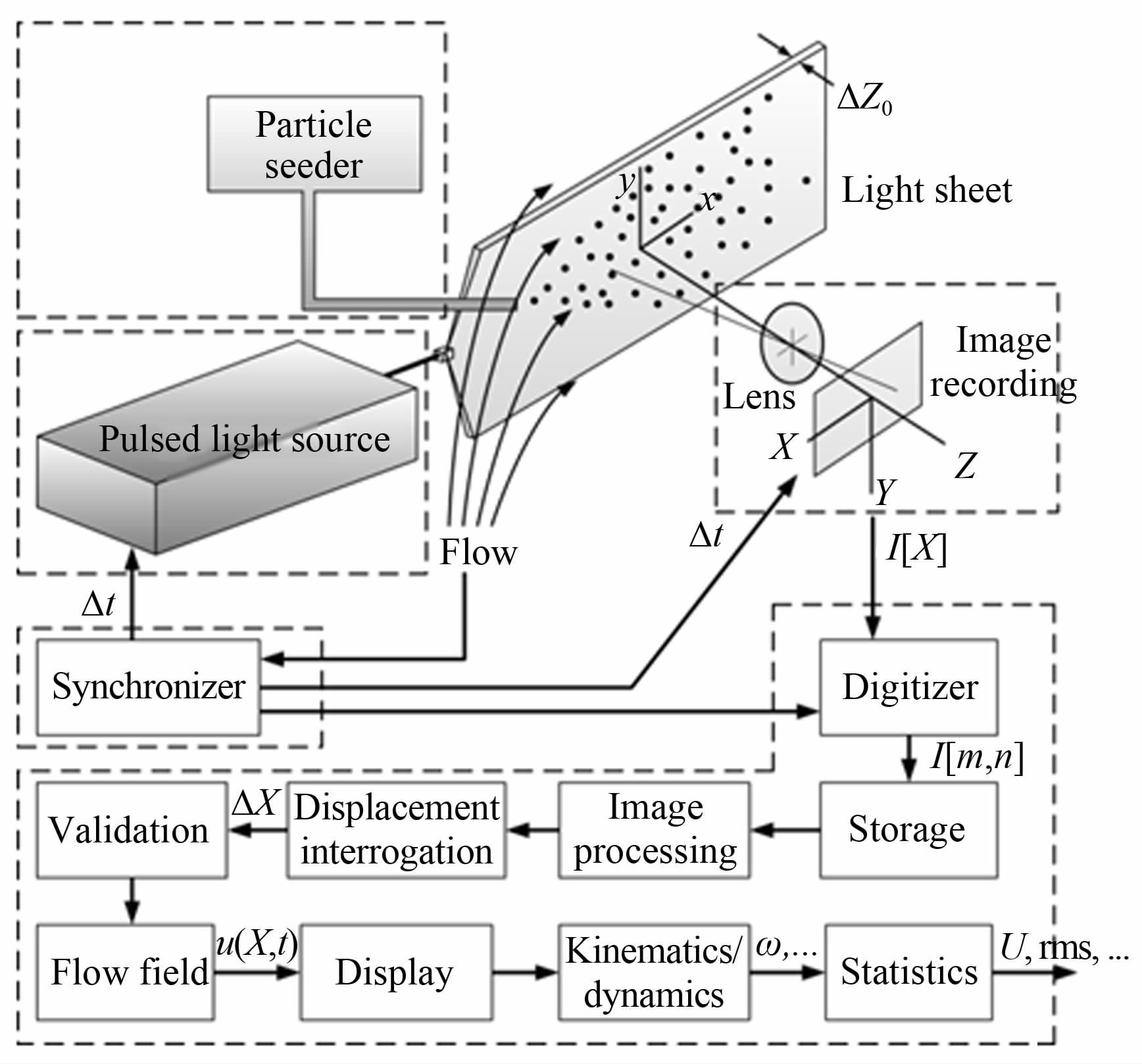
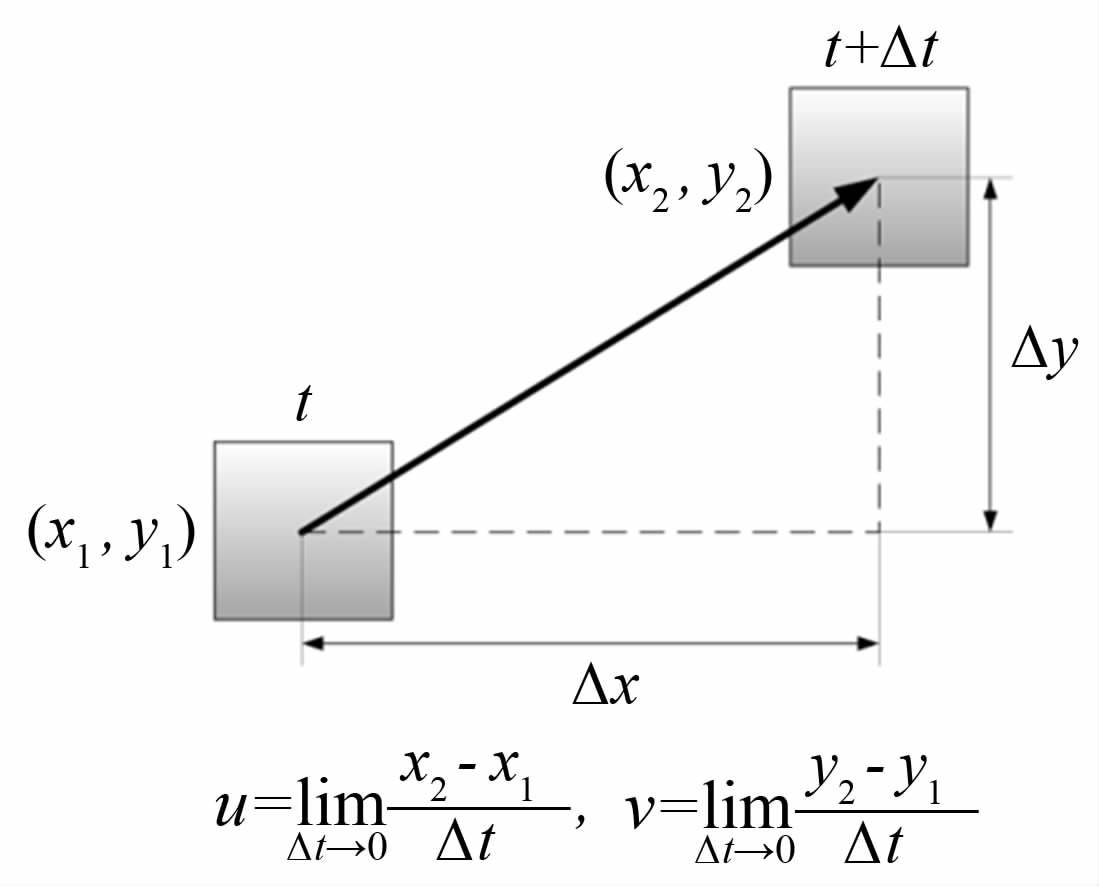
图 1是典型的二维PIV系统部件示意图,根据功能的不同,可以将其分成5个部分:粒子布撒系统、光源、同步器、图像采集装置和后处理系统。其工作过程可以做如下描述:利用粒子布撒器将示踪粒子均匀地分布在主流中,当激光光源照射流场时,粒子将会发生散射,这样图像采集装置(如CCD相机)就能捕捉到粒子在流场中的位置。通常激光发生器会发射一定时间间隔的2个激光脉冲,由于同步器的作用,图像采集装置能够精确地捕捉到2幅清晰的粒子分布图,这2幅原始图像经过数字化、判读区划分、互相关计算等一系列的后处理过程之后,就能得到流场的速度分布。获取速度场的原理图如图 2所示,如果2个激光脉冲的时间间隔足够小,便可认为粒子做轨迹为直线的匀速运动。文献[6]指出,从流场的照明直至速度场的构建都会产生误差,图 1中的每个组成部件都会对测量结果带来1%的不确定度。
|
| 图 2 PIV测速原理示意图 Fig. 2 Principle of PIV measurement |
经过近30年的发展,5个方面的改进[1]使得PIV技术能够应用到精细化复杂流场的测量中。(1) 计算机性能的提高保证了复杂算法的计算能力,使得普通电脑能够计算二维或三维的相关函数。(2) 数字PIV技术的理论已经建立,各设备能够发挥出最佳性能,并且使进一步的优化成为可能。(3) 数码相机的分辨率已经超过1000万像素,使得拍摄的图片具有更可观的清晰度,有能力展示流场中的微细结构。(4) PIV专用相机能够记录纳秒级时间间隔的2幅图像,为更准确描述高速流场打下了基础。(5) 大功率激光器的使用使得相机能够清晰地捕捉到纳米级粒子的散射光强[1]。
高速复杂流场对PIV技术应用有着很高的要求。超声速流动的流场信息相对于低速流场更难捕捉,经过激波时,气流会急剧减速;超声速/高超声速飞行器实际运行环境中气流的高可压缩性和低雷诺数造成附面层过厚,导致激波和附面层之间的相互作用更加严重。在时间尺度和长度尺度上,高速可压缩流比亚声速流要大一个数量级[7],激波带来的局部稀薄效应使得流动的最小长度尺度与分子平均自由程相接近。
在高速流场的PIV实验中,示踪粒子穿过激波,去往低速区,受惯性影响,在这特殊的区域内无法做到完全的流动跟随。甚至会导致测量结果与真实流场之间存在一定程度乃至相当大的偏差[9]。激波不仅形成很大的速度梯度,使得粒子的流动跟随性不可避免被惯性所缚,高可压缩性还造成激波前后粒子浓度差距甚大:示踪粒子浓度变化太大,在低速区集中,在高速区稀疏,造成测量不便、数据处理分析困难。同时,流体介质呈现各向异性,会对粒子散射光的传播路径造成影响,从而影响获得流场数据的准确性[10]。
基于粒子自身惯性带来的不可避免的滑移,粒子流动跟随性迟滞,对高频脉动量响应迟滞。这构成了高速可压缩流场中PIV应用的主要误差[7, 11]。这时,粒子的记录显影与数据处理的难度进一步加大,测量的精度也大打折扣。除了布撒方面要进行改善,还要采取有效的后处理手段。否则测量误差会很大,乃至测量结果中激波出现弥散。
所以,相比于普通流场的PIV测量,应用于超声速气流的PIV系统要求更高,具体体现在光学部件、示踪粒子选择、布撒装置等方面。目前为止,经过研究者们的不懈努力,已经建立起了适用于超声速流动PIV技术的相关理论,并运用该技术在高速复杂流场实验测量领域取得了相应的成果,但该技术在硬件系统及理论方面还有待完善。
1 超声速复杂流动PIV技术研究实践 1.1 光学部件的特殊要求现代PIV系统中的光学部件主要包括相机和激光器。CCD相机是目前PIV系统图像记录的主流设备。CCD是电荷耦合器件(Charge Coupled Device)的简称,它能够将光线变为电荷并将电荷存储及转移,也可将存储的电荷取出使电压发生变化。CCD相机性能参数主要是像素和跨帧时间,像素直接决定了图片的空间分辨率,跨帧时间则决定了PIV技术能够测量的流场速度范围,这2项参数对超声速流场的测量尤为重要。现阶段的跨帧时间已经低至100ns量级,分辨率达到了千万像素(4096pixel×4096pixel)。固体激光器在PIV系统中最为常用,自Kompenhans等人[24]首次将Nd:YAG固态激光器应用于PIV系统中之后,这种特征波长为532nm的激光器得到了大规模的应用。上世纪90年代是Nd:YAG激光器飞速发展的时期,脉冲能量从10mJ[25]提高到了400mJ[26],跨帧时间低至400ns[17],脉冲时间也降至6ns[27]。目前国内的激光器厂商已经能制造脉冲能量高达800mJ的Nd:YAG双脉冲激光器。然而Nd:YAG固态激光器脉冲能量虽高,但重复频率较低,现阶段最高的发射频率也仅仅停留在15Hz左右,这一特点决定了Nd:YAG激光器不适用于时间分辨PIV技术中。而Nd:YLF固体激光器重复频率可以达到10kHz量级[28],但其脉冲能量较低。
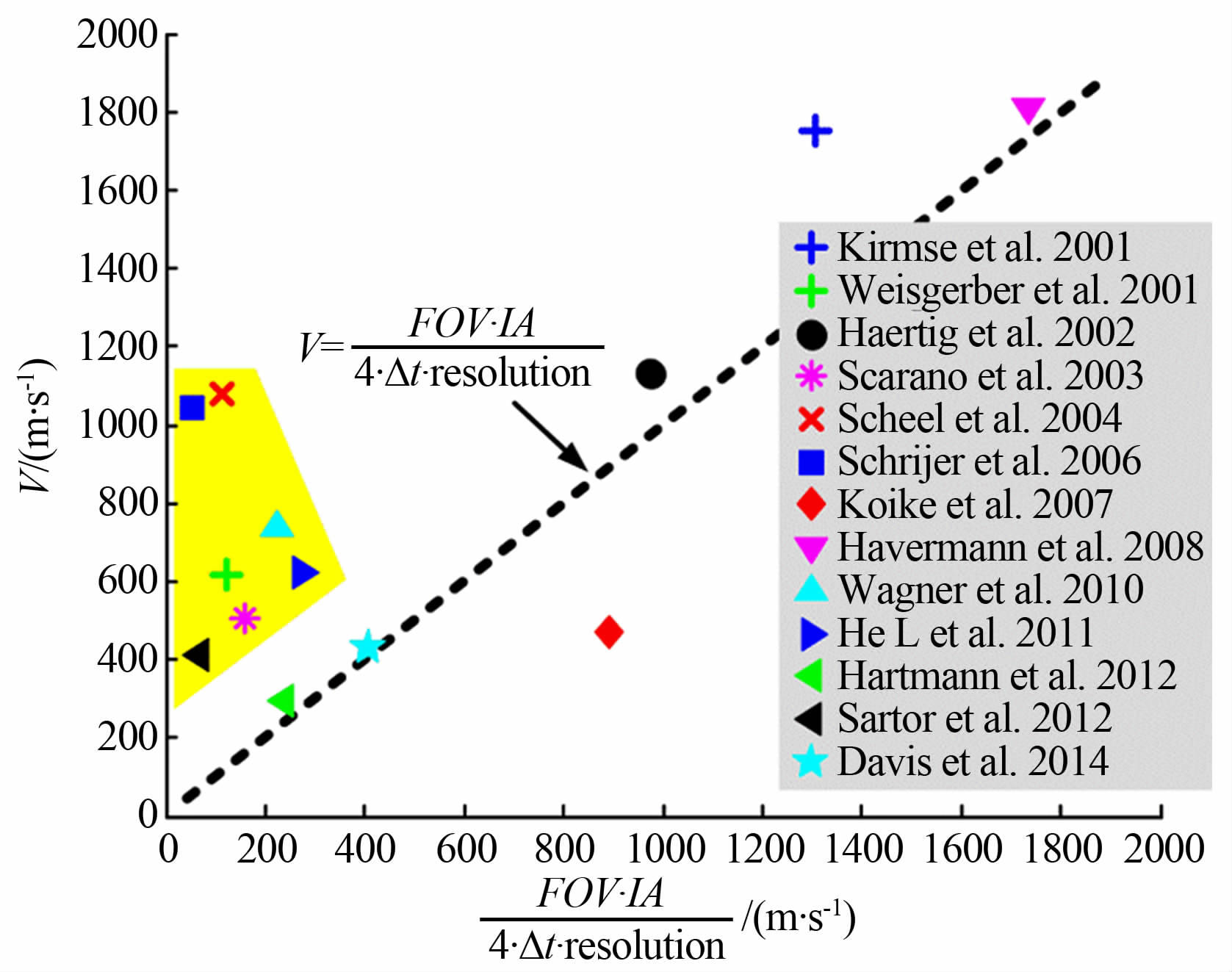
光学部件是PIV系统中的关键部分,从时间分辨率公式$V = \frac{{FOV \cdot IA}}{{4 \cdot \Delta t \cdot {\text{resolution}}}}$可以看出,它的性能也直接决定了PIV技术所能测量的流场速度范围,其中V代表流场的速度,FOV (Field Of View) 代表视场范围,IA (Interrogation Area)表示判读区大小,Δt表示跨帧时间,resolution代表分辨率,目前普遍认为,PIV技术所试用的速度测量范围为0.01~1200m/s。根据此公式,将前人研究工作中流场速度和光学部件参数选择的关系总结成了图 3的形式。以$V = \frac{{\left( {FOV/{\text{resolution}}} \right) \cdot IA}}{{4 \cdot \Delta t}}$作为参考线,可以发现大部分的“点”分布在对角线的左半部分,特别是黄色区域覆盖的区域,这说明在光学部件参数的选择上,$\frac{{\left( {FOV/{\text{resolution}}} \right) \cdot IA}}{{4 \cdot \Delta t}} < V$。单从时间分辨率公式分析,对于判读区大小,往往希望尽可能的减小,以便能够在相同的测量范围内获取更多的速度向量,因此当流场速度提高时,必须减小跨帧时间(Δt)或者增加空间分辨率 (FOV/resolution),而这2个参数恰恰决定了光学部件的综合性能,包括激光器的脉冲时间和最小跨帧时间、相机的像素大小和所能记录2幅图片的最小时间间隔、同步器的控制精度等。由图 3可知,出于各种原因,光学部件的综合性能还不能完全满足所对应的超声速流场的速度测量要求。因此除了提高激光器能量以增加信噪比以外,对于PIV技术应用高速复杂流动,光学部件综合性能的提升还有巨大的空间。
随着跨帧CCD相机和双脉冲激光器的出现,亚微秒的时间间隔使其可以记录1000m/s量级流动速度的互相关图像,PIV技术逐渐开始应用于超声速流动甚至高超声速流动。但是,PIV技术的分析精度本质上决定于示踪粒子的密度、大小和运动响应等物理特性,特别是示踪粒子跟随性在超声速流动中的PIV应用至关重要。示踪粒子的运动特性往往基于粒子在高速流动中跨越激波时的松弛过程,分析其在速度间断面的松弛时间和相应的松弛距离。美国斯坦福大学的Urban和Mungal[29]在试验中发现TiO2粒子的松弛时间大约为3~4μs,而Al2O3粒子松弛时间超过20μs。荷兰代尔夫特理工大学的Scarano和Van Oudheusden[15]通过分析斜激波后的粒子速度
型认为所用的TiO2粒子松弛时间小于2μs。Ragni等人[30]还采用了松弛时间范围0.4~3.7μs的一系列固态粒子进行了系统研究。这些PIV测试都表明,亚微米-纳米尺度的示踪粒子都表现出很好的跟随性,有能力捕捉到超声速流动细节。美国空军技术学院的Huffman等人[31]分别比较了PIV和MTV技术在超声速轴对称射流中的应用,结果发现100nm示踪粒子能够较好地捕捉平均流动特征。
但是,大部分超声速流动试验中,定量分析粒子松弛过程的数学模型仅适用于激波法向马赫数小于1.4的情况,这为更大激波法向马赫数下的流动分析带来了很多的不确定性。虽然,日本东北大学的Koike等人[17]以及荷兰代尔夫特理工大学的Schrijer和Scarano[32]分别提出了一些方法对此进行了修正,但是试验条件对粒子的气动特性和体密度都有着直接影响。接下来本文将进一步开展PIV示踪粒子运动特性的理论和试验研究。
根据德国纽伦堡大学的Melling[33]对固态粒子在气流中的运动特性分析,在BBO方程中仅需考虑粘性项和惯性项。这时,粒子速度Up对绕流速度U的响应为指数衰减关系:
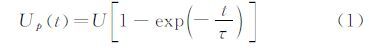
这里t/τ是一个描述粒子运动松弛过程的关键参数。式中τ为粒子运动响应的示踪时间,可以表示为:
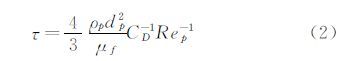
其中,CD为阻力系数,粒子雷诺数Rep则由粒子速度和流动速度之间的相对速度给出:
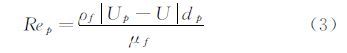
μf是气流的动力粘度,而ρp和dp分别为粒子密度和当量直径。
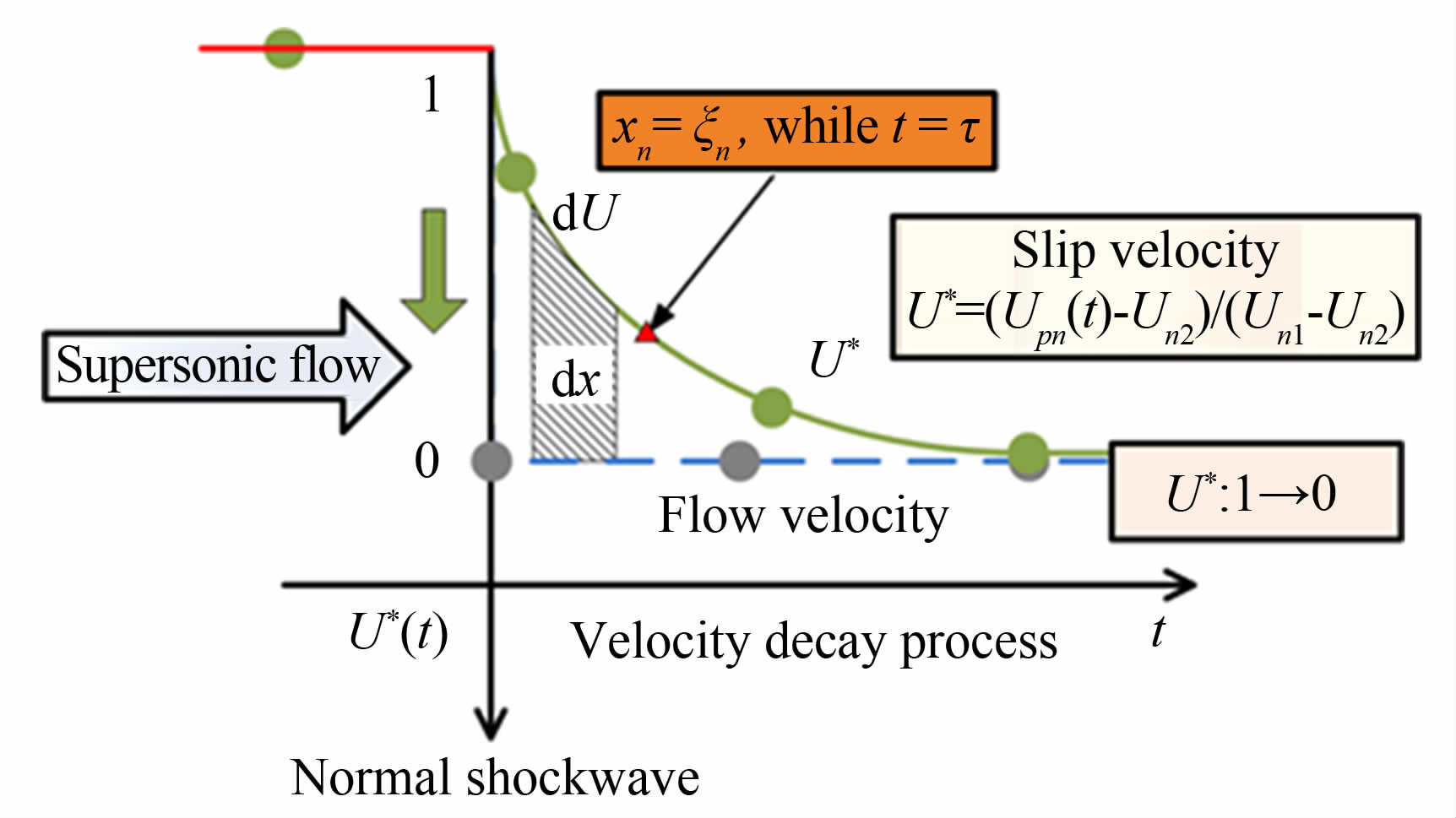
如图 4所示,示踪粒子跨越激波之后将会以指数衰减规律逐渐减速,并恢复到波后气流速度。这里假定所有示踪粒子在激波附近区域混合均匀,由此引入无量纲滑移速度U*:
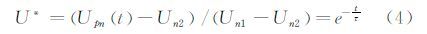
式中,Upn(t)为粒子法向速度,Un1和Un2分别为激波前后的气流速度。
|
| 图 4 超声速流动中示踪粒子跨激波运动特性 Fig. 4 Dynamic characteristics of a particle crossing a shock in supersonic flow |
Dring[34]和Tedeschi[35]对于粒子跨激波的流动现象进行了深入的分析,如Haertig et al[14],Urban and Mungal[29],Amatucci[36]等将其用于分析粒子惯性运动。在大部分超声速流动试验(Schrijer et al[16],Ragni et al[30],Ghaemi et al[37])中,小角度尖楔绕流诱发的斜激波法向马赫数都小于1.4。Melling[33]提出了一个近似模型,认为当激波法向马赫数小于1.4时,粒子松弛过程表现为线性关系,即:
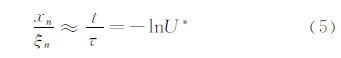
其中,xn为是粒子经过运动时间t(即,PIV相机的跨帧时间ΔT)的法向位移,ξn为粒子跨越激波的法向松弛距离。
但是,高速流动试验研究中的法向马赫数明显高于这个假设条件,Melling公式在更强激波条件下不大适用。上海交通大学陈方等[38]通过在[0,t]时间间隔内进行积分之后,引入无量纲松弛距离x*=xn/ξn提出了一个新的分析模型:
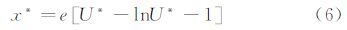
其中,粒子松弛距离
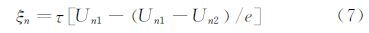
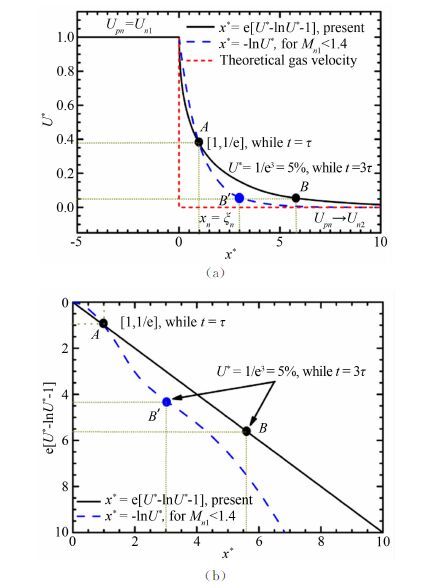
图 5对2个分析模型进行了比较,结果发现:Melling模型滑移速度U*变化较剧烈,法向马赫数较大(>1.4)的情况时与实际相差较大,低估了高速流动中示踪粒子的松弛距离,不能准确反映强间断下粒子的松弛过程。相对而言,新模型没有引入假设条件,适用于更高马赫数下的松弛过程。粒子在A点之前的运动衰减更快,之后则由于惯性相对较慢。当粒子速度恢复到波后气流速度的95%时(即e-3=5%,B点),粒子松弛距离大约为Melling模型计算值的2倍。
|
| 图 5 粒子跨激波的速度变化曲线 Fig. 5 Velocity variation of a particle across a shock |
考虑正激波关系式,可以得到如下公式:
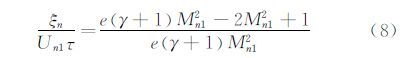
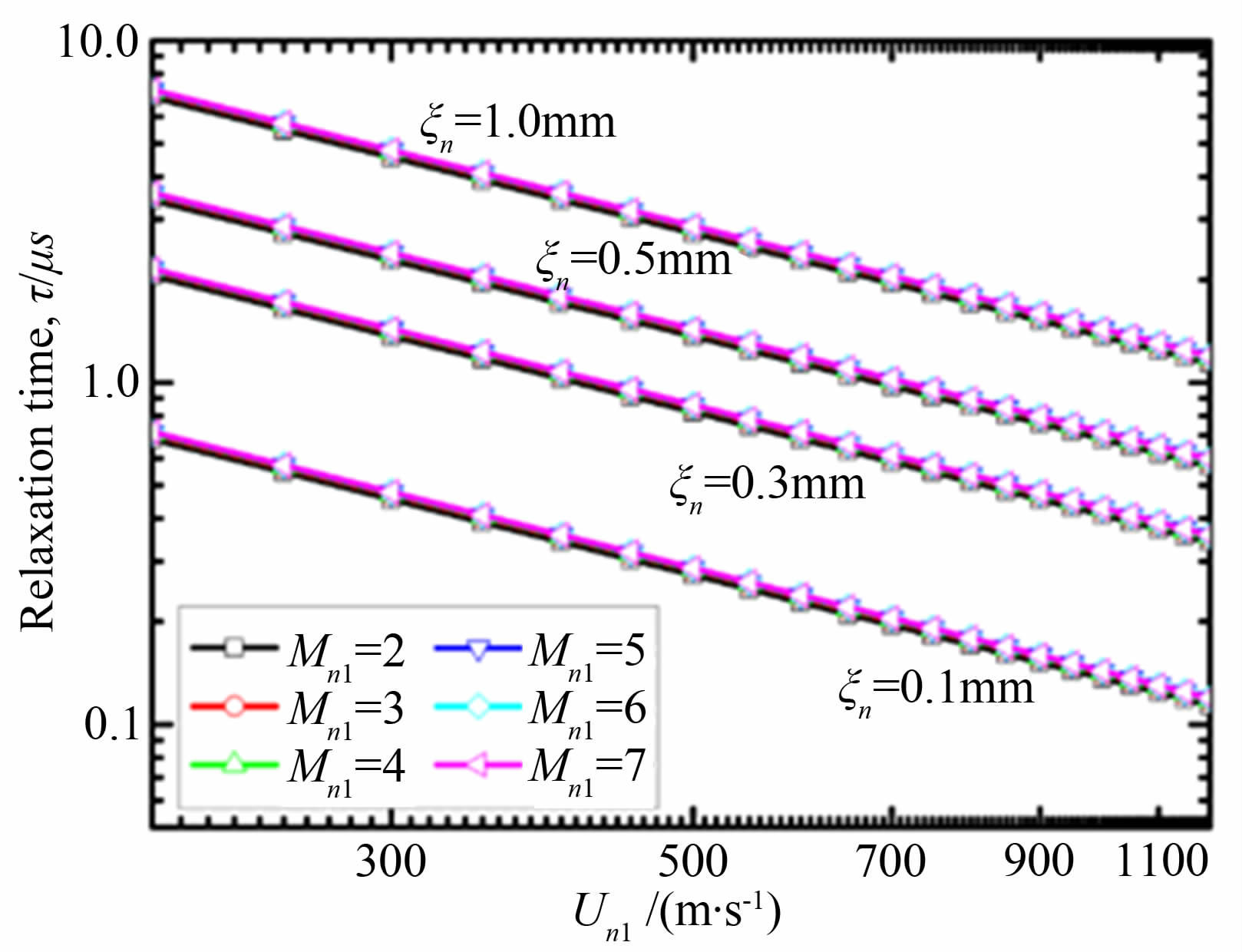
由此,可以给出激波强度Mn1、激波前流动速度Un1以及松弛时间τ的相互关系。从图 6可以看出,激波强度Mn1的影响并不大,而波前流动速度Un1和粒子松弛时间τ基本成反比。显然,粒子松弛时间τ越小,高速流动中PIV测量的可信度越高。
|
| 图 6 粒子运动参数关系 Fig. 6 Particle motion parameters |
为了确定示踪粒子大小选择的配置准则,这里引入半弹性函数(Wooldridge[39]),即:
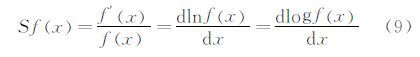
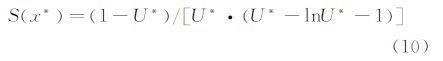
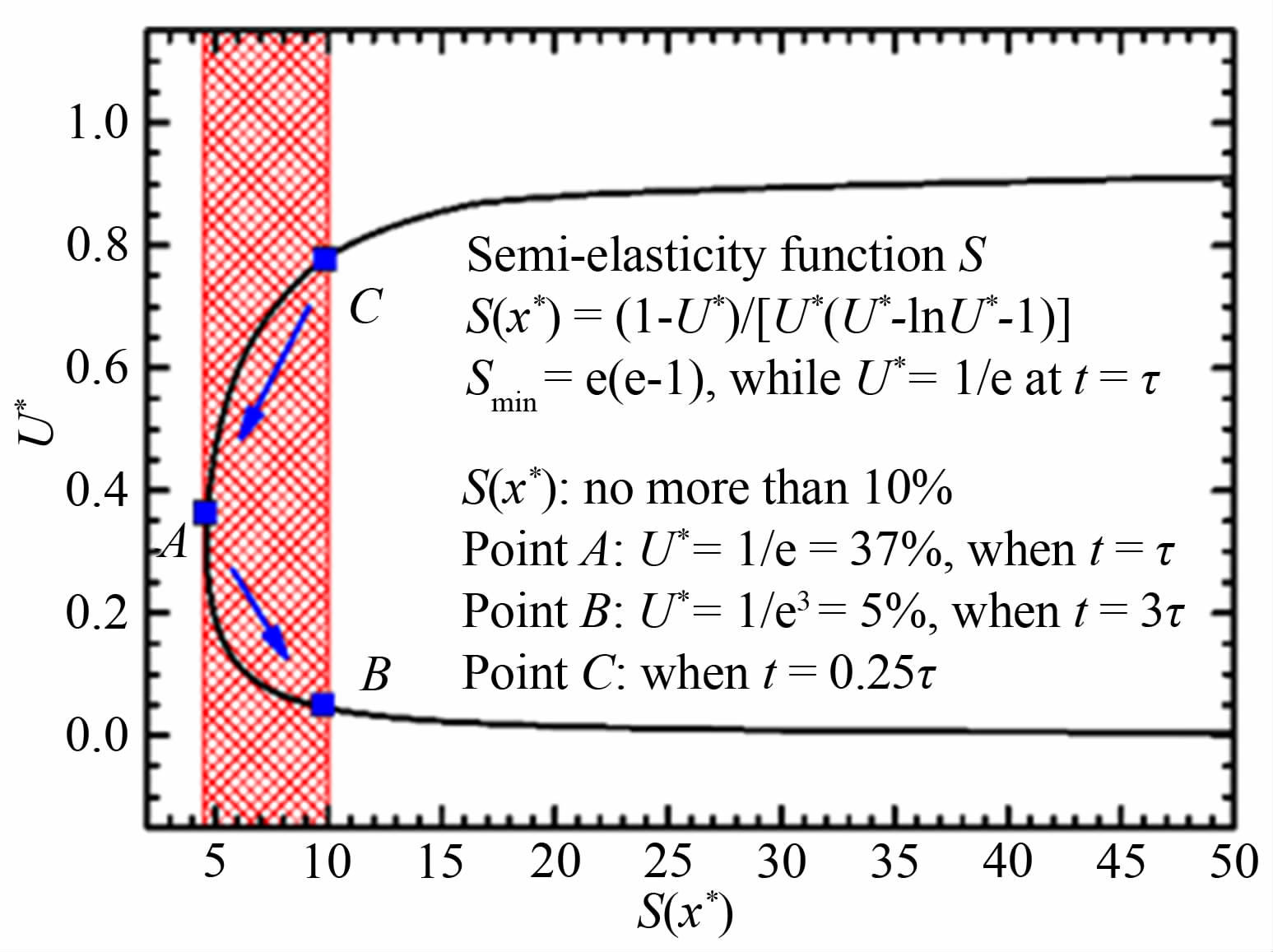
如图 7所示,当t/τ在0.25~3范围内(从C点到B点)变化时,粒子滑移距离x*随粒子滑移速度U*的变化不超过10%。这也表明,这样的粒子滑移时间使PIV测量对粒子跟随性的敏感度小于10%,可以保证足够的粒子跟随性。因此,这个关系式将作为高速流动PIV示踪粒子的选择准则。
|
| 图 7 粒子滑移过程的半弹性函数 Fig. 7 Semi-flexible function of a slipping particle |
如果粒子雷诺数Rep较小(Rep$ \ll $1),粒子阻力系数可以根据Stokes定律[40]给出,即:

这种线性关系只能适用于不可压缩和连续流动,但是可以反映粒子的基本运动关系,由此可以直接给出粒子松弛时间与粒子直径之间的关系:

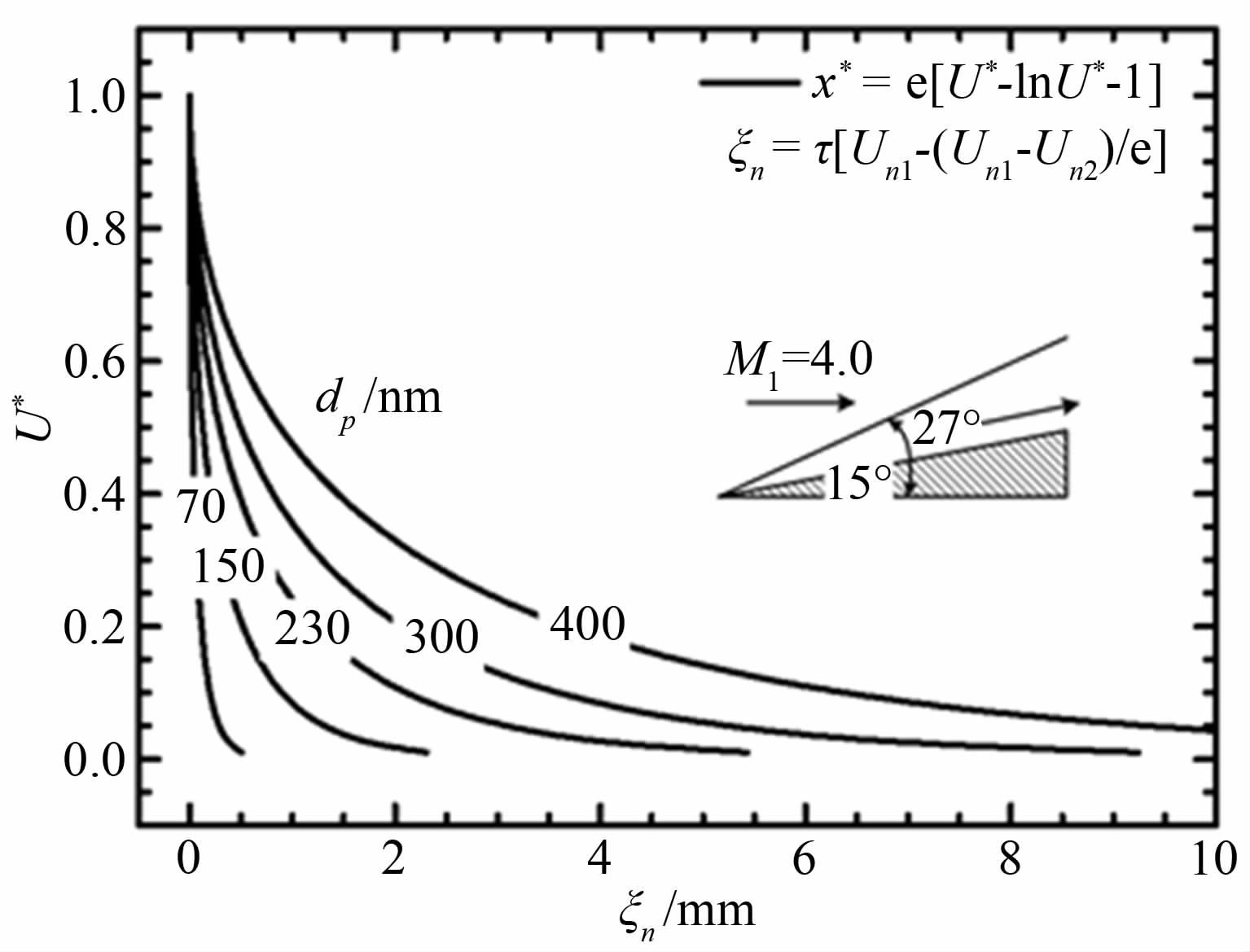
图 8表明不同尺寸粒子的松弛过程。上海交通大学多马赫数风洞Ma=4高速气流(800m/s),测试条件为静压3.1kPa和静温96.4K,气体动力粘度μf=6.4×10-6Pa·s。根据待测区域的流动速度,PIV时间间隔为500ns。在此条件下的15°尖劈模型试验中,尖劈头部诱发一道约27°的斜激波。很显然,粒子越小,粒子松弛距离越短。针对TiO2粒子(密度4.23×103kg/m3),要满足t/τ在0.25~3,示踪粒子应该为70~230nm。当示踪粒子为70nm时,粒子速度将在0.5mm左右恢复到波后流动速度。
|
| 图 8 Ma=4流动中粒子跨激波松弛过程 Fig. 8 Relaxation of particles across a shock in a Ma=4 flow |
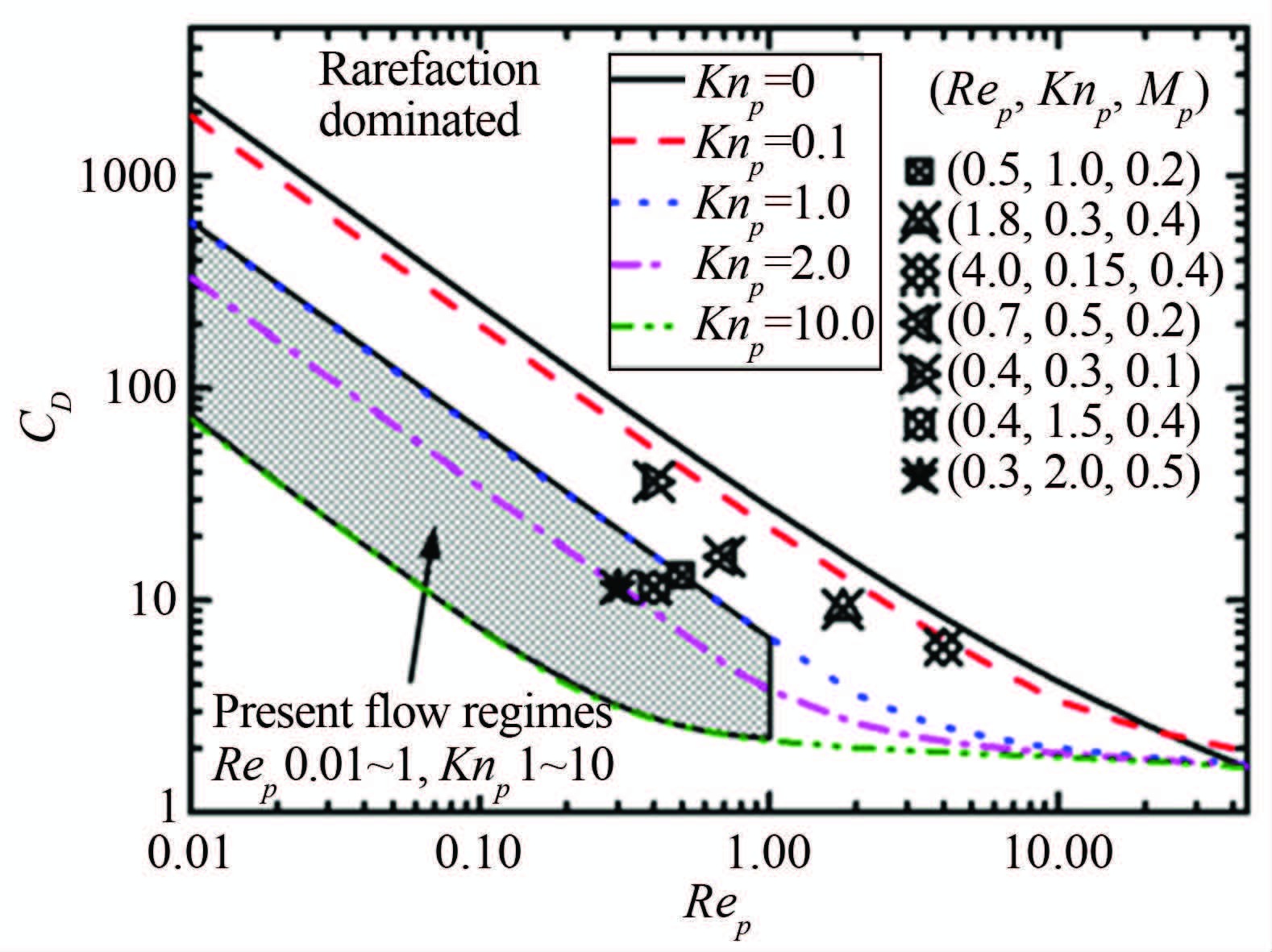
但是,在超声速或高超声速流动中,Stokes律往往失效,还需要考虑到可压缩效应,引入相对马赫数Mp,即
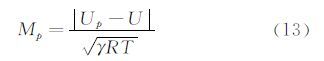
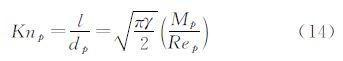
| Rep | Knp | Mp=Knp·Rep·$\sqrt {2/\pi \gamma } $ | |||
| 参数范围 | 0.01≤Rep≤10 | 0.1≤Knp≤10 | 0.4≤Mp | ||
| 流动特性 | 层流 | 过渡流动 | 可压缩流动 | ||
| 参考文献 | Rep | Knp | Mp | PIV测试 | |
| Tedeschi et al[35] | 0.5 | 1 | 0.2 | 斜激波,来流条件:M=2.3,U=550m/s,latex: 500nm | |
| Scarano et al[15] | 1.8 | 0.3 | 0.4 | 可压缩尾迹,来流条件M=2,U=504m/s,TiO2: 500nm | |
| Koike et al[17] | 4 | 0.15 | 0.4 | 横向射流,来流条件:M=1.8,U=460m/s,dioctyl sebacate: 1 μm | |
| Humble et al[66] | |||||
| Ghaemi et al[37] | 0.7 | 0.5 | 0.2 | 斜激波,来流条件:M=2,U=504m/s,TiO2/Al2O3: 500nm | |
| Ragni et al[30] | |||||
| Mathijssen et al[67] | 0.4 | 0.3 | 0.1 | 三角翼,来流条件:M≈2,U=500m/s,Aerosol: 700nm | |
| Chen et al[38] | 0.4/0.3 | 1.5/2 | 0.4/0.5 | 斜激波,来流条件:M=4/7,U=800/1200m/s,TiO2: 300nm | |
Loth[41]给出了考虑可压缩效应和稀薄效应修正的粒子阻力公式:
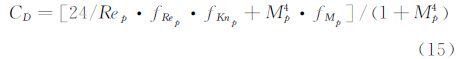
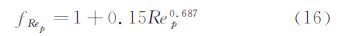
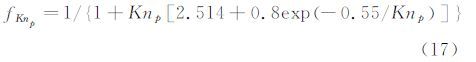
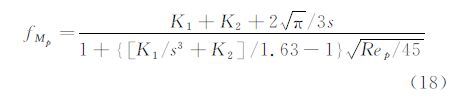
其中,
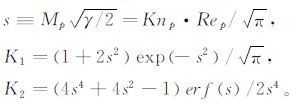
因此,在高速流动(1<Rep<45)中,粒子松弛时间与粒子直径平方为非线性关系,不再满足公式12。这就意味着,高速流动PIV试验对粒子跟随性提出了更高的要求。在上述Ma=4尖劈流动PIV试验中,采用经过修正的阻力计算模型(公式(15)-(18)),要满足粒子选择准则t/τ=0.25~3,粒径应该在20~50nm,才能够更好地捕捉高速流动。
1.3 示踪粒子及其布撒技术PIV技术的基本原理是通过测量示踪粒子的位移确定速度场,因此示踪粒子的选择尤为重要。一般对示踪粒子的要求有2方面[42]:(1)良好的散射特性,以便拍摄的图像具有高的信噪比,这就需要粒子的粒径不能过小。(2)优秀的跟随性,这样得到的速度场才能够更加真实地反映实际流场,所以粒子的粒径要足够小。可见这2方面的要求是相互矛盾的,实际选择往往要折衷考虑,该矛盾在超声速流场中的示踪粒子选择上尤为突出。此外,从安全性角度出发,示踪粒子还应该具备对人体无毒无害、对设备无腐蚀性和化学反应惰性等特点。同时,实验结束后在设备中的残留污染少。
在超声速PIV实验中的用到的示踪粒子可分为固态粒子和液态粒子。常见的固态粒子有SiO2、Al2O3、TiO2等[30],其中SiO2的散射特性较好,但熔点低,Al2O3的熔点高,但散射特性一般,而TiO2同时具备散射特性好、熔点高的优点[43],因此应用更加广泛。
粒子越小,其运动松弛时间越短。Urban[44],Goyne et al[45],Scarano和Van Oudheusden[15]等人在研究中发现,30nmAl2O3和TiO2粒子的松弛时间接近。但是,这些纳米尺度粒子将不可避免发生聚团现象而使其有效粒径增大一个数量级。相比而言,Al2O3粒子更容易聚团,比如300nm粒子聚团之后将凝结成块,达到2~40μm[15]。TiO2粒子相比较其他可用于布撒的粒子材料,具有较高的折射率,使得它作为示踪粒子更加可靠。TiO2粒子的气动特性、成本和操作性上都有更大的优势[29],TiO2粒子尺寸完全可以适应高速流场各种脉动尺度,因此成为在高速流动测试中的最佳选择[16]。
PIV技术要求的粒子布撒浓度比较高,在激波、大尺度的涡区以及强剪切层等高速流场结构中应用PIV技术,是比较难以获得优质结果的。为了对流场中精细的结构加以分析,对粒子有光散射性高和流动跟随性好的要求。除此之外,还需要被布撒的粒子具备合适并尽量接近平均值的粒径,均匀地散布在流场之中。这样才能消除过大粒子带来的过强影响以及小粒子类似于背景噪声的干扰,得到一个更接近事实的结果分析。因此,粒子布撒器决定了布撒效果的优劣。
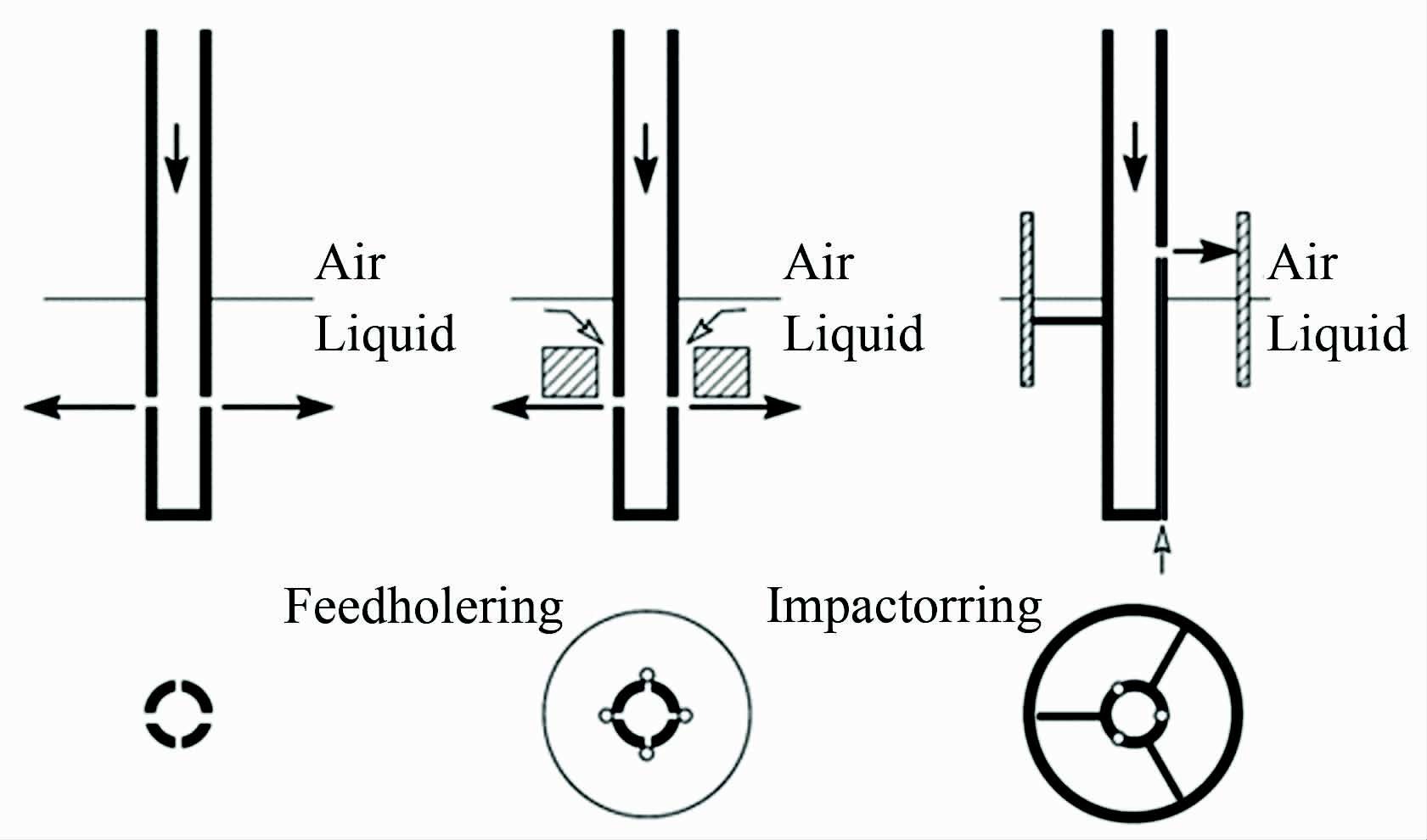
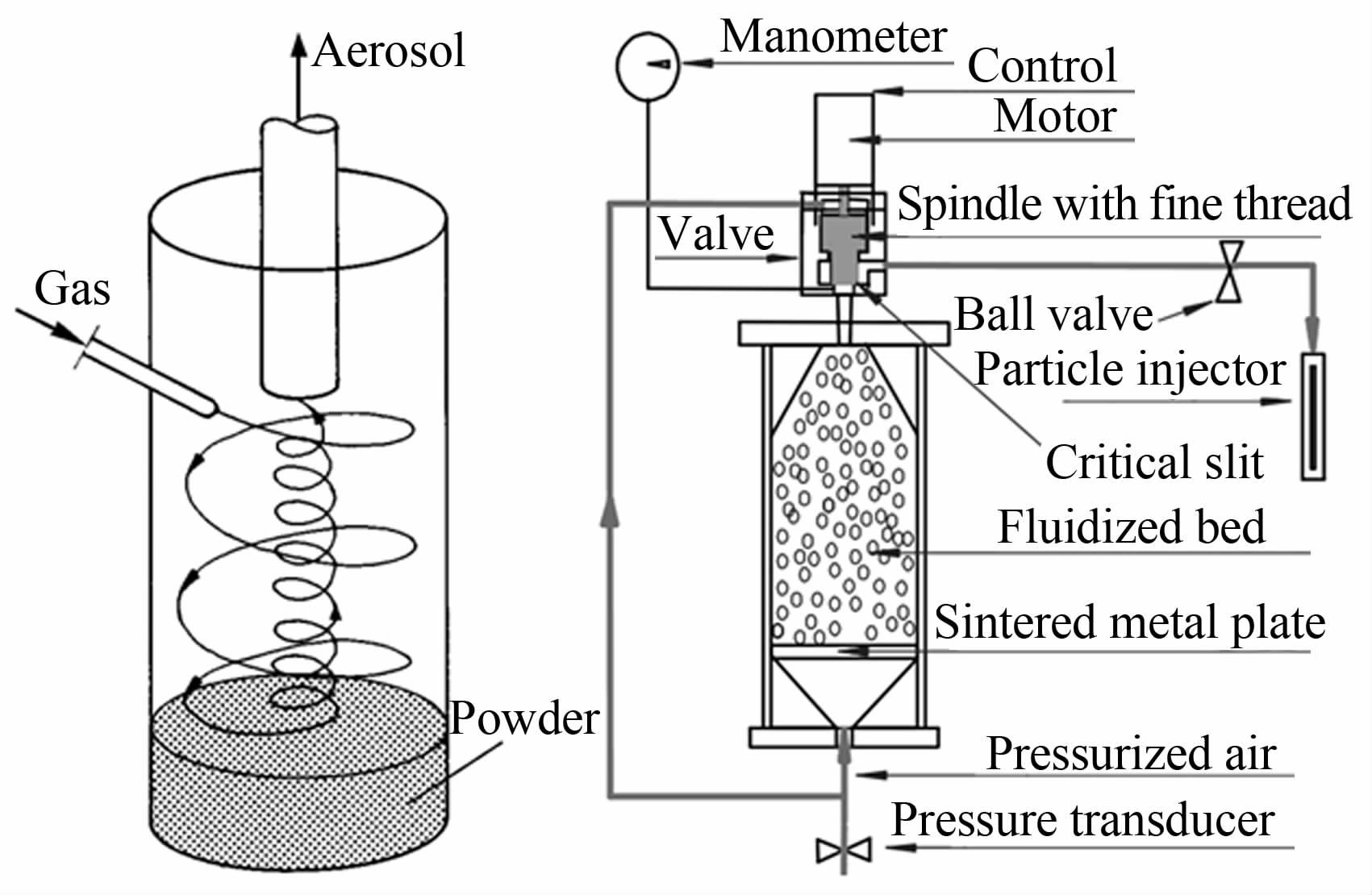
传统的固态粒子发生器可以分为旋流式和流化床式两大类,两类粒子发生器都是利用高速气流和粒子充分混合进而形成气溶胶,通过布撒管路将高粒子浓度的气流加注到主流中,具体形式见图 10。虽然研究者们已经在粒子发生器的形式和结构上做了一系列的改进,但由于超声速PIV实验粒子布撒的难度,目前粒子浓度的控制还停留在经验判断阶段,浓度是否合适主要依靠实验结果做进一步的调整[1]。
|
| 图 10 固态粒子发生器 Fig. 10 Solid particle seeder |
Ragni[30]等人分别用了旋流式、流化床式和Laskin喷嘴式的粒子发生器,比较了不同种类、粒径的固态示踪粒子和雾化后的癸二酸二辛酯(DEHS)液滴在穿越激波后的跟随特性,首次证明了固态粒子的松弛时间能够小于400ns。从松弛时间判断,固态粒子是否脱水、粒子发生器是否安装滤网对结果影响很大,而DEHS的跟随特性好于大部分布撒条件下的固态粒子。
高速流动条件下,PIV测量要求超细和不易发生聚团的示踪粒子。而这些亚微米或纳米示踪粒子非常容易因为潮湿或储存等原因而结块,因此必须采用高效粒子布撒装置对结块粒子进行破碎或清除。Melling[33]总结了很多常用的粒子布撒技术及其试验装置,这些布撒系统需要尽可能在不扰动气流的条件下提供相对均匀的粒子分布。为了在PIV测试区域保证粒子和气流能够充分混合以保持均匀性,粒子往往需要在风洞稳定段进行添加。而稳定段的运行压力和温度都非常高,如Ma=4流动大约在400K和2MPa。这也要求示踪粒子的注入压力至少要高于主流压力1~2MPa,才能保证示踪粒子进入稳定段。如此高压的技术要求,对目前常用的粒子布撒技术提出了极大的挑战。
为了更好地解决以上问题,本文提出了如图 12所示的粒子布撒系统,结合了流化床和旋流器等技术,在布撒装置中形成了类似“龙卷风”的高压、高动量的粒子流。利用高压干燥气体为驱动气体,最大工作压力可以达到12MPa,可携带粒子浓度变化范围为0.01~0.2kg/s。在耐压能力达到16MPa的旋压成型粒子容器中,隔绝纳米粒子与含有水蒸气的空气接触,在纳米粒子周围形成防潮保护层。可以在高温(1000K)和高压(16MPa)环境下工作,结合操作流程和控制时序便于加注和清理粒子,能够实现气溶胶的流量可控、快速均匀混合和防潮,气溶胶中示踪粒子平均直径能够达到纳米量级,解决了高速高压示踪粒子技术的粒子跟随性和布撒问题。
|
| 图 12 上海交通大学PIV示踪粒子布撒系统 Fig. 12 Particle seeder system in SJTU |
热线风速仪(Hot-Wire Anemometry,HWA)是一种基于传热学的速度测量方法,具有高的空间分辨率和频率响应,信噪比极高,然而它属于入侵式单点测量,布置于流场中的热线会对流动产生扰动,这对于高速复杂流场的测量可以说是致命的缺陷,因此对于低速湍流度较弱的流场来说,HWA是一种理想的速度测量方法。激光多普勒测速法 (Laser-Doppler Velocimetry,LDV)是另一种常用的流场测试手段,其原理是利用多普勒效应,通过测量散射光的频率变化从而得到速度值。LDV同样具有高的空间分辨率,而且属于非入侵式测量,适用于高度湍流测试,但单点测量的劣势同样制约着这种方法的进一步推广。
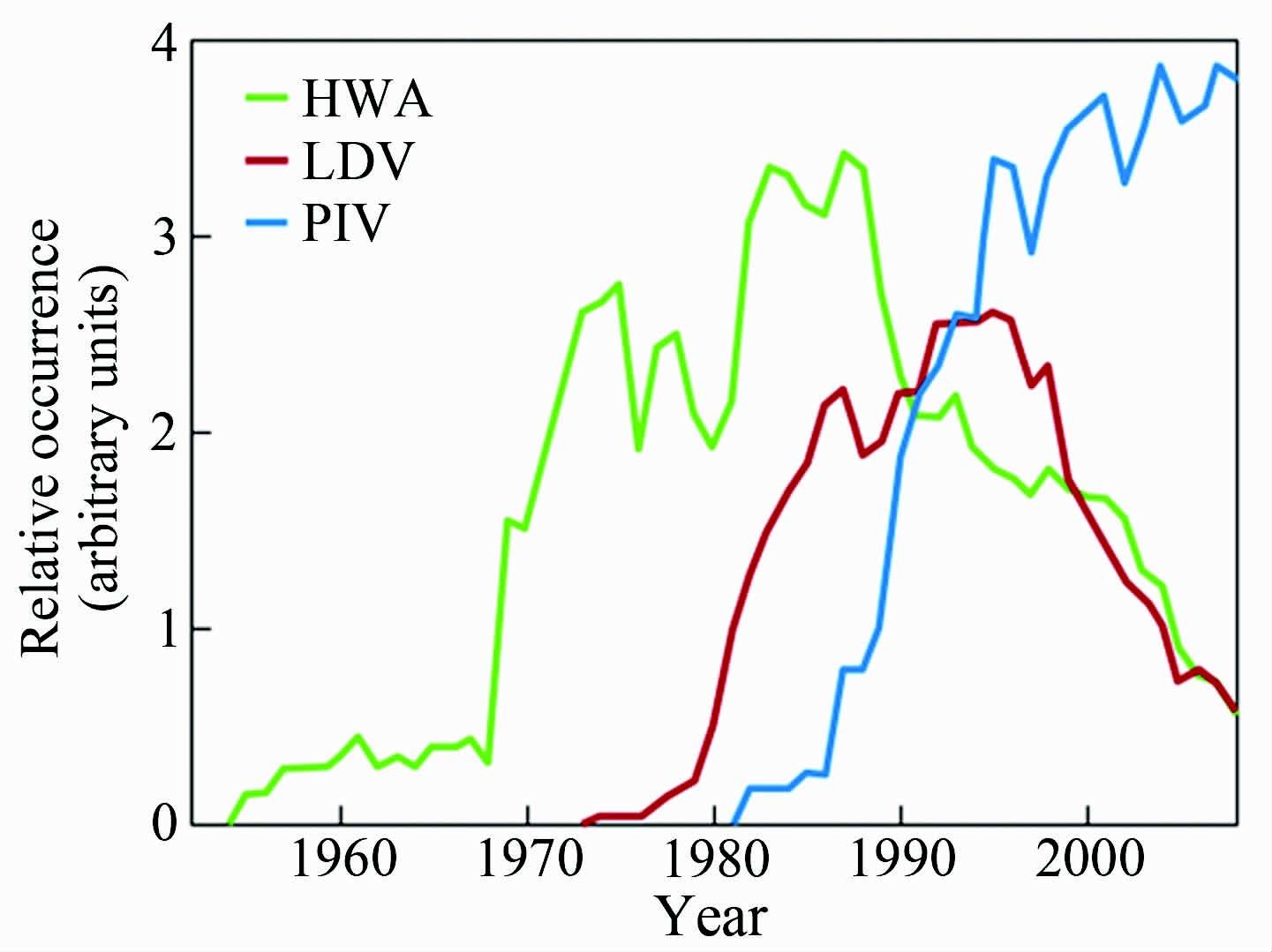
相比之下,PIV这种非入侵式全场测量方法在高速复杂流场测试中已经展现出了不可比拟的优势。以平面PIV技术为例,除了激光的热效应和引入粒子有可能对流场产生影响[47]之外,可以说没有其他的干扰因素,这对于超声速复杂流场的测量是极为有利的,同时,全流场测量大大提高了效率。PIV技术另外的一个优点是速度的矢量化测量,这就使得后续计算涡量场等深度流场信息挖掘成为了可能。此外,基于平面PIV测量方法衍生而来的诸如时间分辨PIV技术、体视PIV技术、全息PIV技术等,能够极大地帮助研究者们认识湍流脉动、三维结构流动等一系列复杂流场。虽然PIV技术还存在精度、空间分辨率、信噪比低等缺陷,但不妨碍它成为应用最广的流场测量技术。这一点,Google Ngrams中关于这3种速度测量方法的文章数量统计(如图 13所示),也从另一方面体现出了近年来PIV技术相比于HWA和LDV在研究者中的受欢迎程度。
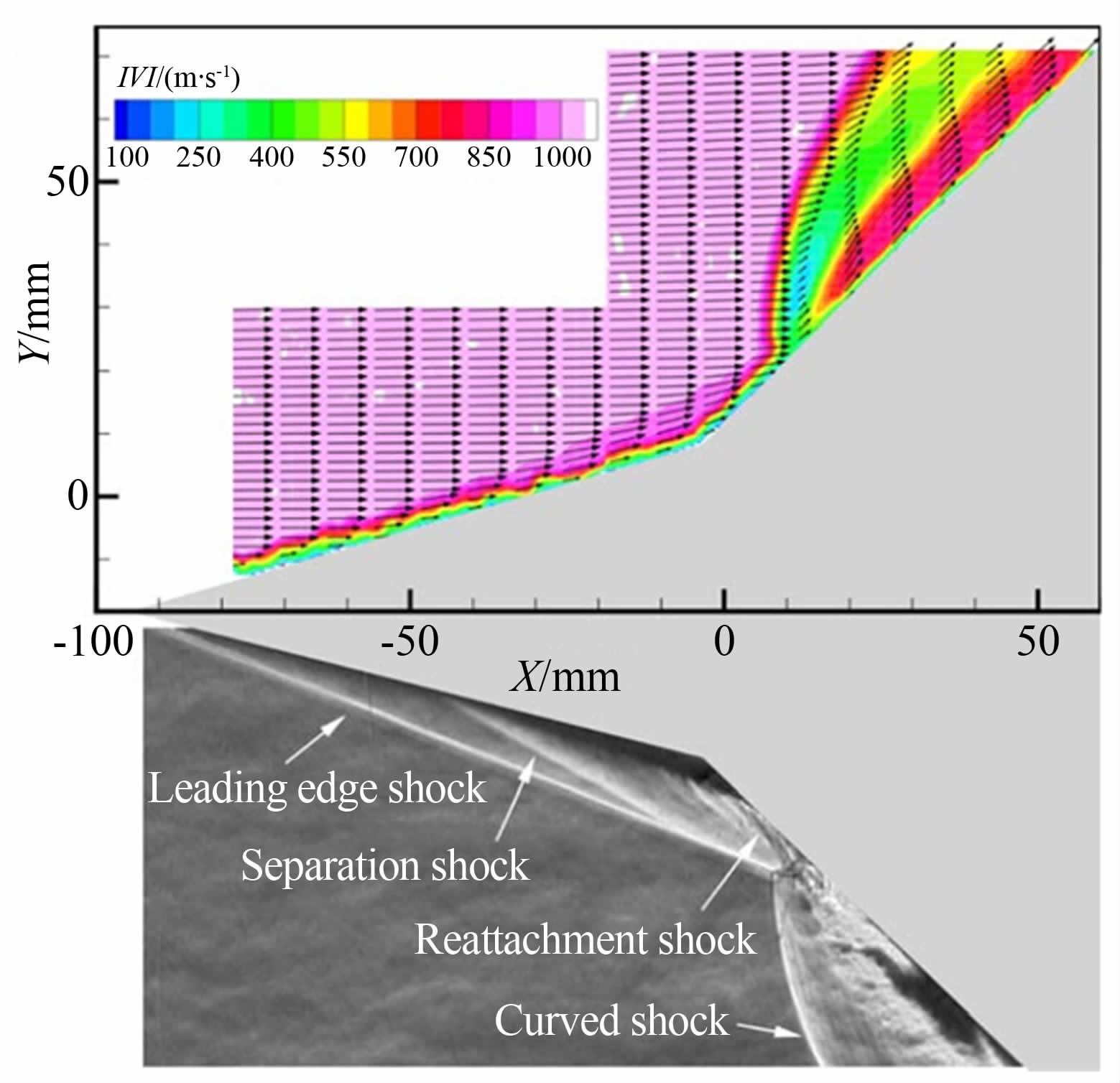
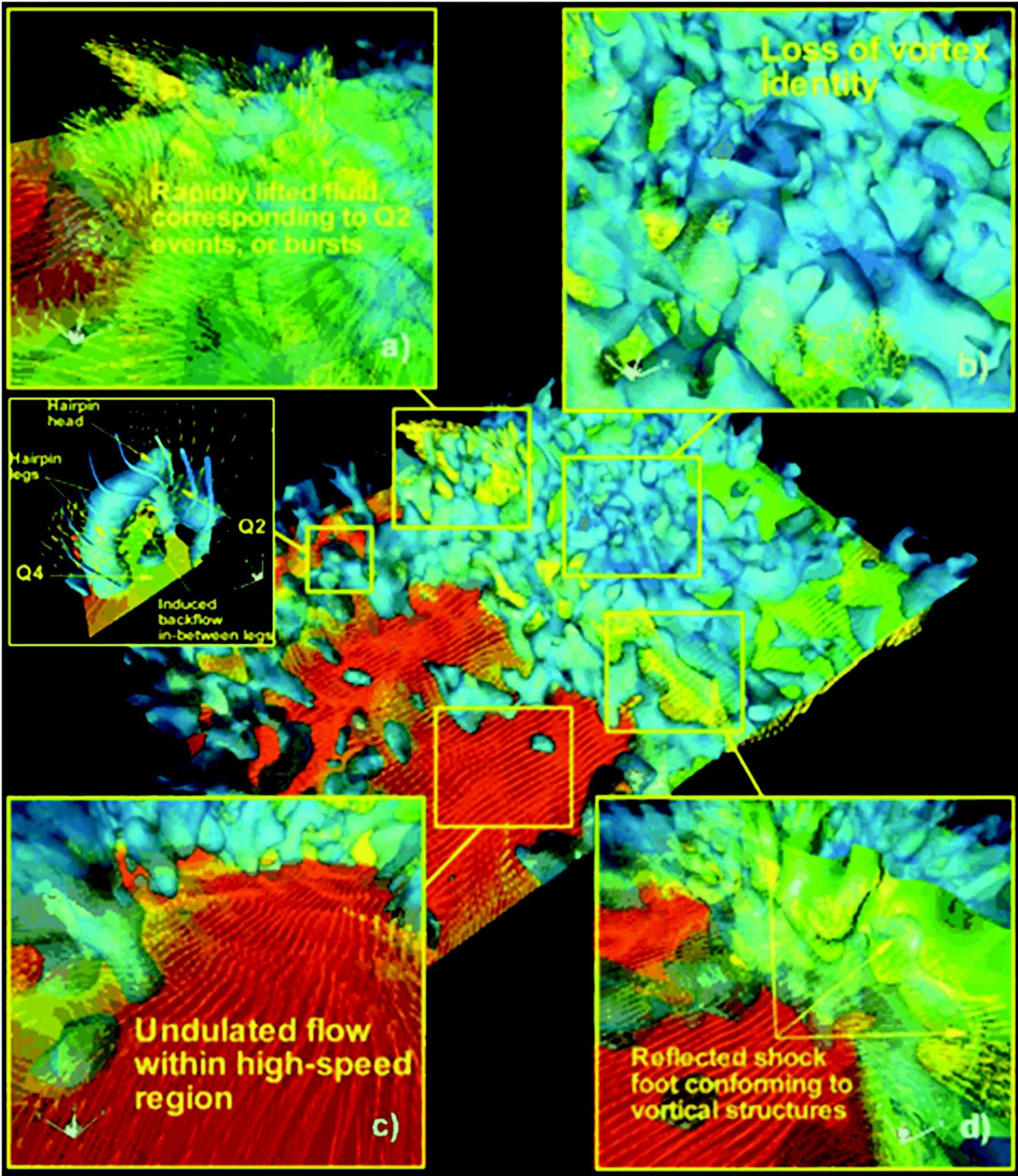
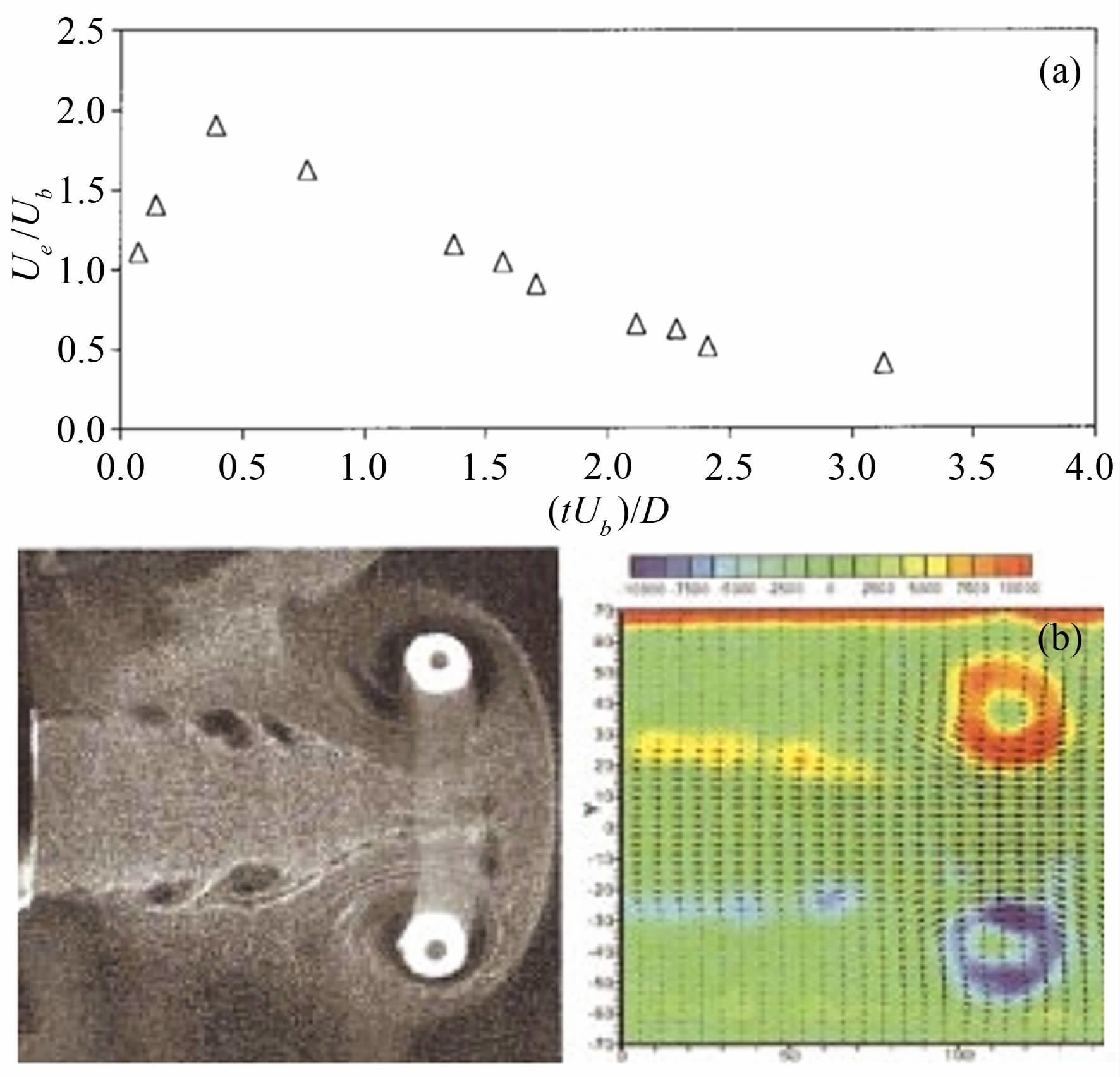
利用PIV技术研究激波流场方面,Haertig[14]等人将PIV技术应用于高马赫数激波风洞(Ma=3.5和4.5),激波前后测得的速度值与理论值做了比较,首次证明了PIV技术在高速、短历时流场中的适用性,但是受空间分辨率的限制,速度场的云图粗糙,捕捉激波波面能力较弱。Scarano等人[16]将PIV技术应用到了高超声速流场(Ma=7,1043m/s)的测试中,作者将双尖劈模型的PIV测量结果、纹影结果(如图 14所示)和理论值做了比较,指出除了激波面附近(厚度为2倍的松弛距离)和近壁面处,PIV技术能够对高超声速流场做定量化研究。从图 14可以看出,PIV技术在捕捉激波面的能力与纹影技术相比还存在差距,且弯曲激波(curved shock)波后速度场的准确性还有待商榷。以激波边界层相互干扰为代表的高速复杂流场一直是人们的研究热点,PIV技术的进一步发展为观察超声速边界层内的流场结构提供了条件。Ganapathisubramani[49, 50]研究了Ma=2流场中湍流边界层内的流动结构,发现了与不可压缩边界层内类似的大尺度拟序结构,展示了不同壁面法向距离平面内拟序结构的形态,指出可压缩湍流边界层内的对数区域范围比不可压缩边界层内的大。文献[22]详细描述了跨声速流动中激波诱导分离对激波-边界层相互干扰的影响。利用时间分辨PIV技术,机翼近壁面处的激波与分离流的动态相互干扰得到了展示[21]。进一步的,Theunissen等人[51]在近壁面处采用了自适应判读区选择技术,增大了近壁面法向的空间分辨率,能够更精确地展示激波边界层相互干扰的流场结构。另外,平面PIV技术也被用于涡流发生器的高度和位置对边界层分离概率和反射激波不稳定性影响的定量化研究中[52],指出分离区的大小与近壁区的动量通量密切相关,虽然涡流发生器不能完全消除分离区,但能显著增加反射激波的稳定性。而利用最新的层析PIV技术 (Tomographic PIV)[53],激波/湍流边界层相互干扰的三维涡结构得到了很好的展示,发现了跟不可压缩边界层内类似的大尺度拟序结构[54],得到了反射激波形态的测量结果,对激波形态进行定量分析,其结果能够与DNS计算结果对应[55],其中边界层内的多尺度结构如图 15所示[54]。层析PIV技术也被应用于研究涡流发生器的尾迹结构,实验结果能够清晰地观察到尾迹和主流间的剪切层内K-H涡的形态,作者指出流向涡和K-H涡的相互作用使得尾迹结构更加复杂[56]。在超声速漩涡流场的PIV研究中,Havermann[18]和Arakeri[48]等人克服粒子布撒和时序控制等困难,分别研究了激波管出口涡环的演化过程,典型速度场如图 16(b)所示[48]。图 16(a)中,t和D分别代表时间和激波管直径,Ub和Ue分别代表激波管出口处流体的初始速度和流体速度随时间的变化值,即Ub=Ue(t=0),由该图可以发现,在Ue衰减至0之前会先加速到2倍的初始速度,这体现了可压缩性对激波管出口流体速度衰减过程的影响。文献[57]和文献[23]分别研究了超声速流场中存在横向射流的流场结构和超声速射流剪切层内的流场特征,其中文献[23]利用PIV技术研究了利用微射流(Microjet)对控制自由射流和冲击射流不稳定性和噪声的有效性,证明了PIV技术在定量研究多速度尺度流场结构的适用性。
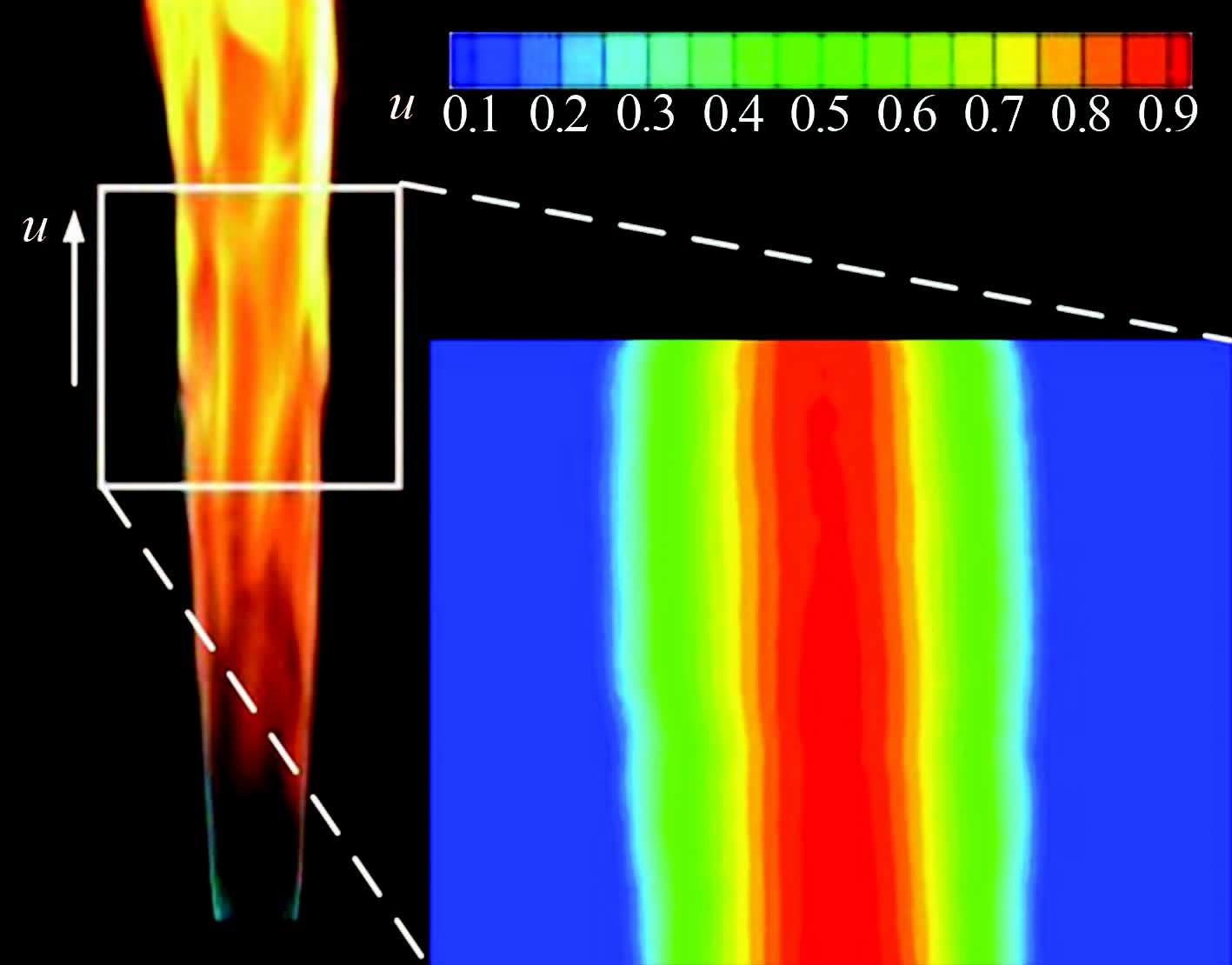
在燃烧场的测试领域,Clemens[58, 59]等人用PIV技术测量了低速射流火焰区(约3m/s)的速度场分布,如图 17所示,并结合LII方法分析了火焰区内的碳烟的形成机制。而早在2001年,就已经有学者将PIV技术引至超燃冲压发动机燃烧室流场的测试中[13],分别测量了混合区、点火区、燃烧区的速度场,目的是研究燃料射流和主流间混合层的结构。文献[8]以公称粒径为12nm的SiO2作为示踪粒子,用平面PIV技术比较了2种不同几何结构的氢气喷嘴对超燃冲压发动机燃烧室冷态流场、燃烧流场的影响,为燃料喷嘴的结构选择提供了依据,典型速度场分布如图 18所示,其中图 18(a)为冷态流场,图 18(b)为燃烧流场。从图 17可以发现,利用PIV技术测量低速射流火焰可以得到较为满意的平均速度场,而在超燃冲压发动机燃烧室流场中(见图 18),由于受限空间、激波、射流和燃烧等因素导致大范围的多尺度区域,流场过于复杂,该文献中得到的冷态和燃烧流场的测试结果均难以反映出精确的速度场。
超燃冲压发动机的研究热潮势必吸引着研究者们去定量化认知发动机燃烧室流场中的精细结构,而超燃流场是超声速复杂流场的典型,其包含了激波、激波/边界层相互干扰、边界层分离、高速漩涡流、速度多尺度、高温燃烧等超声速复杂流场中PIV技术应用的所有难点。如本节所述,即便研究者们针对高速复杂流场的某一特定问题开展了PIV的定量化研究并取得了一定的成果,但是目前为止利用PIV技术精确测量超声速燃烧流场的报导鲜有公开,其原因可归结为现阶段常用的示踪粒子和布撒技术无法满足测量需求。因此迫切需要寻找在燃烧流场中具有高信噪比的示踪粒子和发展适用于大速度梯度复杂流场的粒子布撒技术,才能让超燃冲压发动机燃烧室流场的PIV精确测量成为可能。
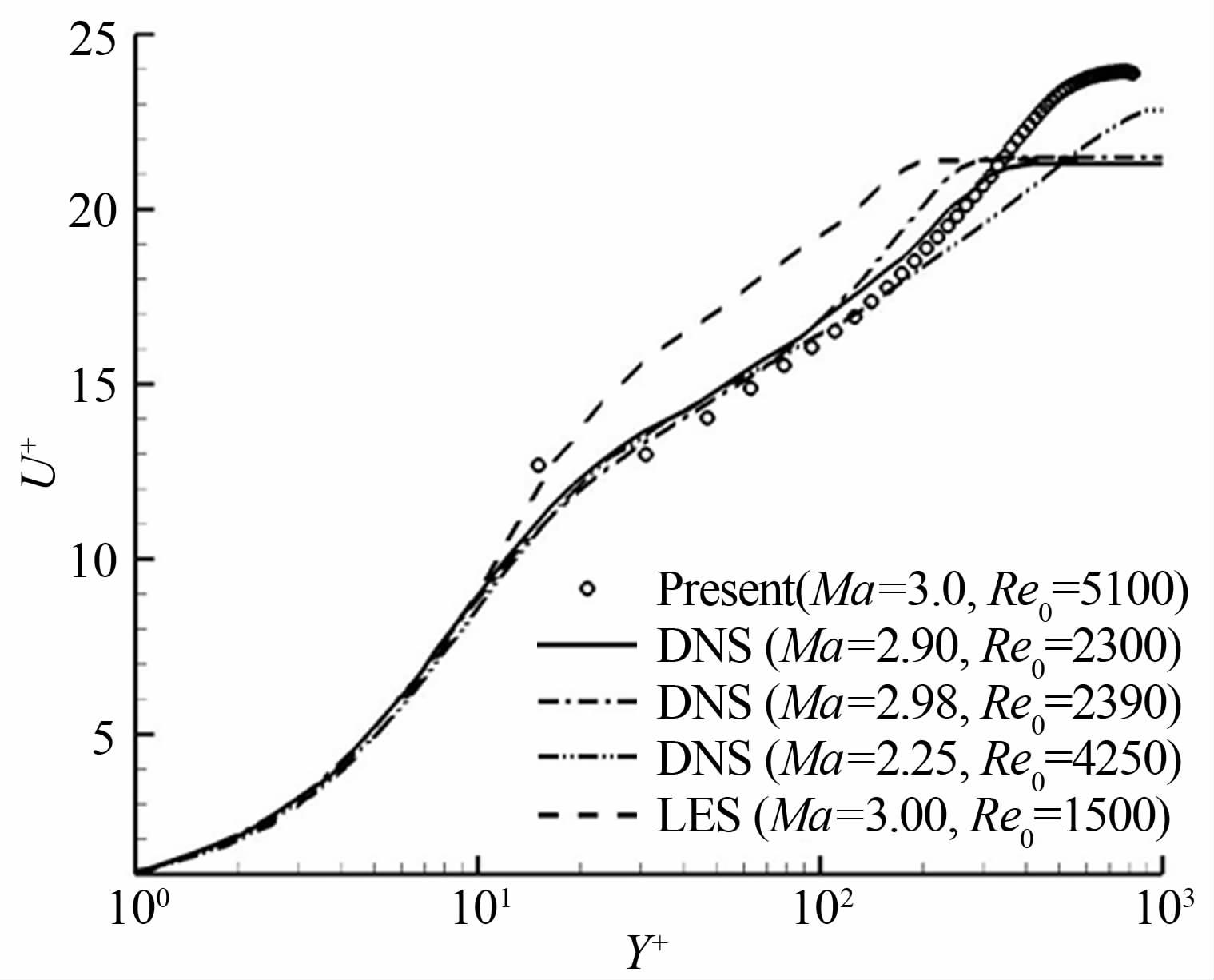
2.3 国内超声速复杂流场的PIV研究成果国内的研究者中,国防科学技术大学易仕和教授的团队利用PIV技术研究了Ma=3流场中平板湍流边界层内的拟序结构和统计学特性[20],得到了与文献[50]相同的结论,边界层平均速度型的实验结果与数值结果符合较好(见图 19)。而文献[60]利用PIV技术获得了激波与层流/湍流边界层相互作用的速度场和涡量场,同时应用NPLS技术得到了激波边界层相互干扰的精细流场结构。
上海交通大学高超声速创新技术实验室在超/高超声速流场测试中PIV技术的应用研究方面做了许多富有特色的工作。实验研究方面,配备有多马赫数超/高超风洞(见图 20)、大能量(500mJ)可变发射波长的激光器和高分辨率CCD(4000pixel×2672pixel)相机,具备开展超/高超声速PIV实验理想的流场、光源及图像采集条件。具体实验参数,即多马赫数风洞及PIV系统的详细介绍见文献[38, 61, 62, 63]。

|
| 图 20 多马赫数风洞-PIV系统示意图 Fig. 20 Pictures of Multi-Mach wind tunnel and PIV system |
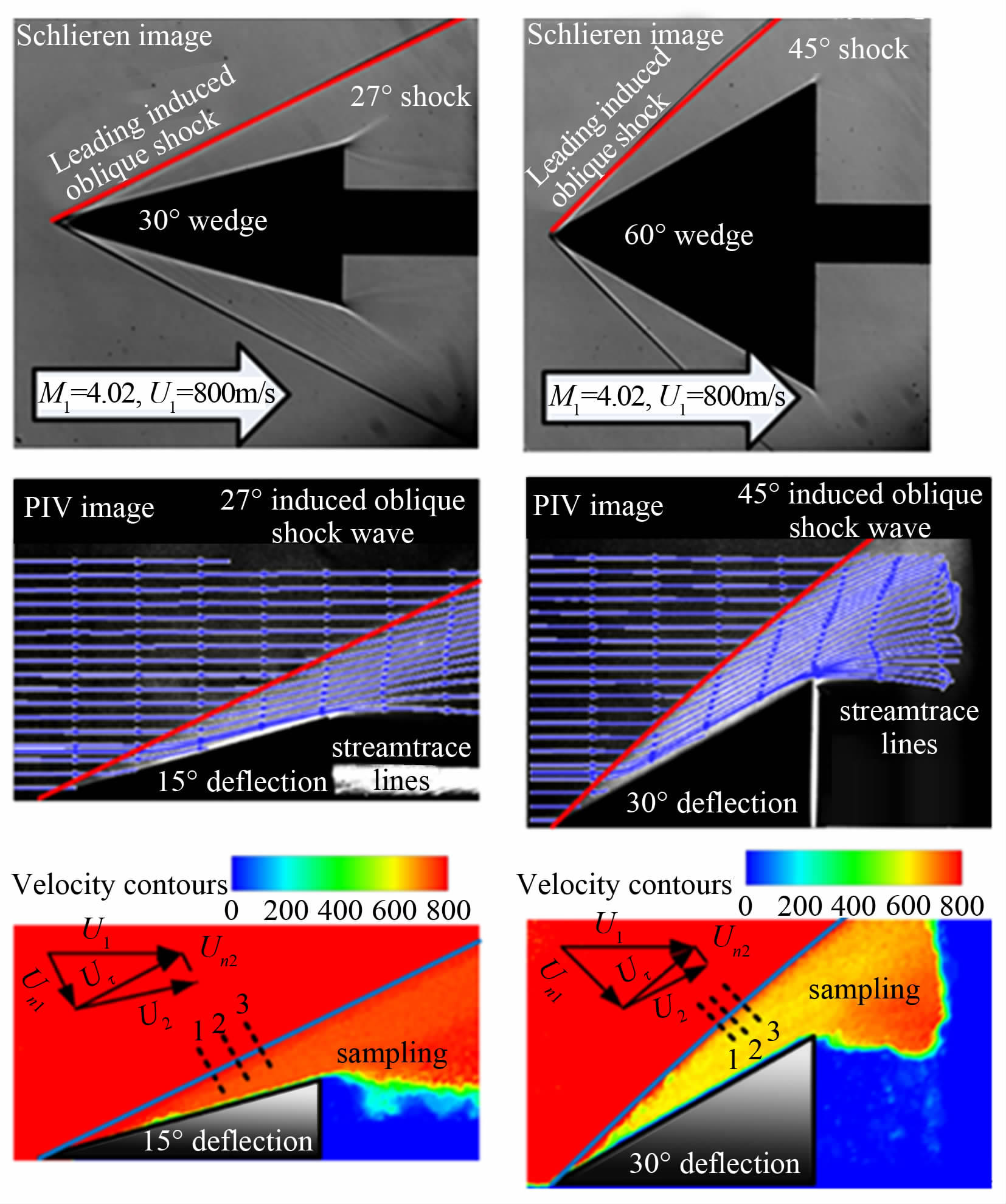
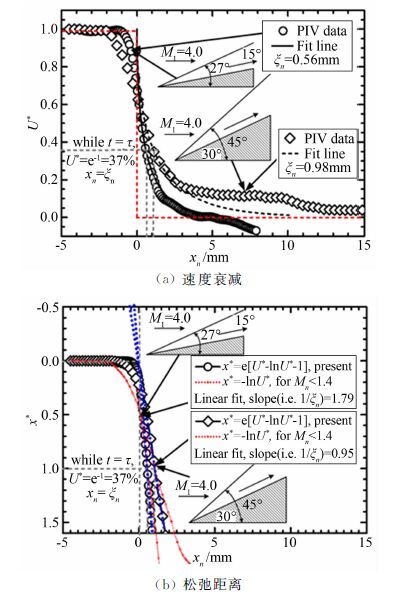
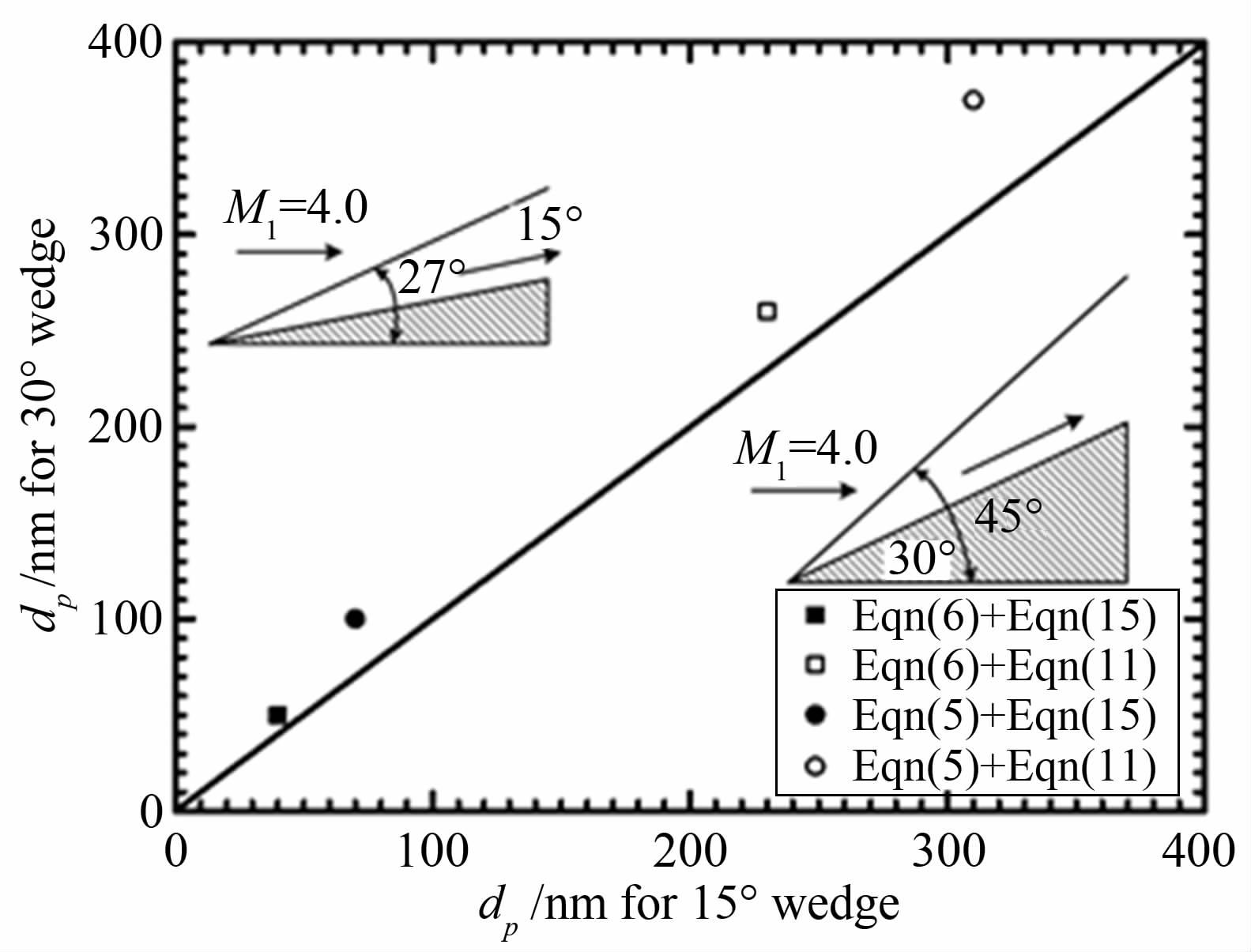
在激波流场PIV试验中,分别采用了半角为15°和30°的尖劈模型,示踪粒子采用标称直径为30nm的TiO2粒子。从图 21中可以看出,尖劈前缘诱导了一道附着斜激波,测量结果与纹影图和理论值吻合非常好。在激波法向位置进行取样以后,可以得到PIV测量的激波法向速度。如图 22所示,根据前文给出的粒子跨激波的速度衰减模型(公式(6)),给$\phi $出粒子的松弛距离分别为0.56mm(15°尖劈)和$\phi $1.05mm(30°尖劈),继而根据公式7可以确定示踪粒子松弛时间τ。结合阻力修正公式(15)~(18),很容易给出尖劈试验待测区域粒子的实际尺寸。如图 23所示,示踪粒子大约为40~50nm,完全可以满足高速流动中对粒子跟随性的要求。而且,粒子直径接近于标称值,这一结果也从另一个角度证明了粒子布撒装置的能力,可以有效解决粒子潮结问题。
|
| 图 21 尖劈试验测量结果 Fig. 21 Experimental results of sharp wedges |
|
| 图 22 PIV测得的激波法向速度分布 Fig. 22 Distribution of PIV measured velocity on the normal component of the shock wave |
|
| 图 23 示踪粒子的气动直径 Fig. 23 Aerodynamic diameters of the tracer particles |
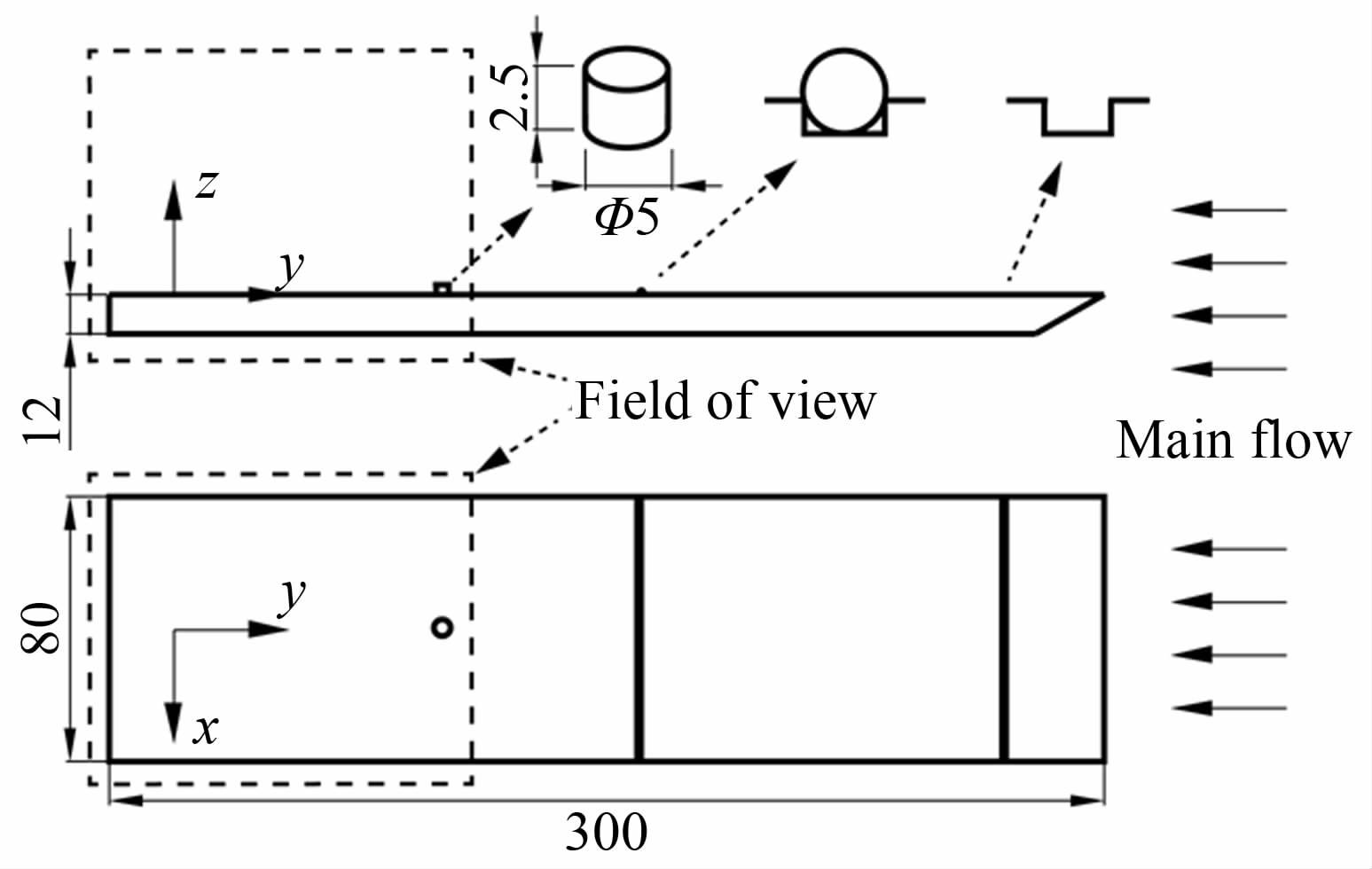
在此基础上,又开展了超声速平板湍流边界层相关的实验研究工作,平板模型见图 24。模型尺寸为L×W×H=300mm×80mm×12mm,在距前缘200mm处有一个直径5mm、高度2.5mm的圆柱型凸起,重点观察凸起物下游的湍流边界层形态。同时,为了使边界层提前转捩,在圆柱凸起上游加了2种形式的转捩带:分别在距离前缘30和140mm处开了宽度1mm、深0.5mm的凹槽,并在140mm处的凹槽上布置有$\phi $1.25mm的铜线。根据拍摄视场和CCD相机的分别率可知,空间分辨率为$\phi $0.045mm/pixel,在后处理过程中,选取的判读区大小为16pixel×16pixel。从实验拍摄的原始图像看,湍流边界层厚度在4mm左右,因此能够较为准确地捕捉到湍流边界层的结构。在Ma=4流场(总温400K,总压2.5MPa,Re=1.4×107/m)中分别对x-y平面和y-z平面(见图 24)做了测量。
|
| 图 24 平板模型示意图 Fig. 24 Schematic of the plate model |
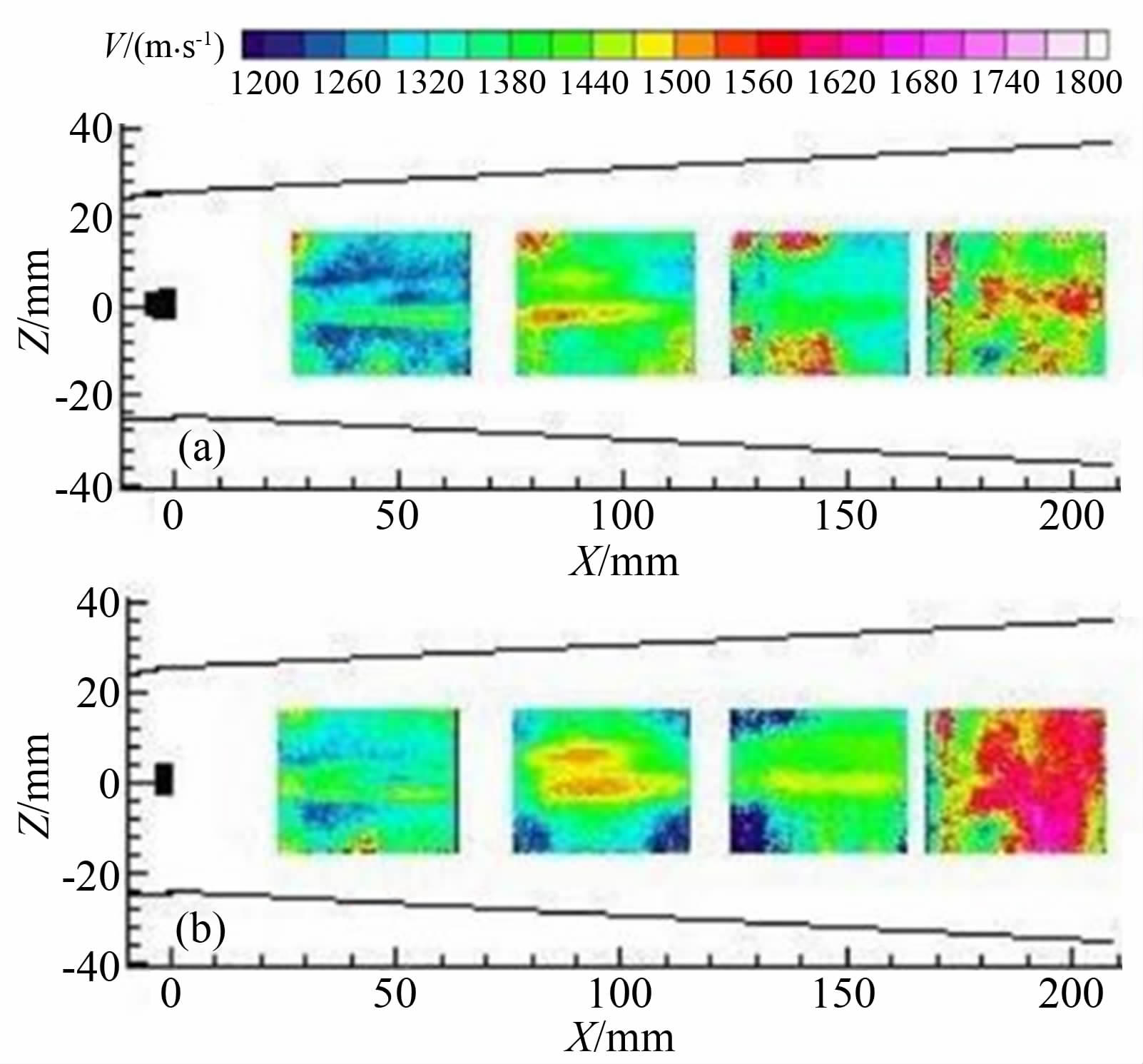
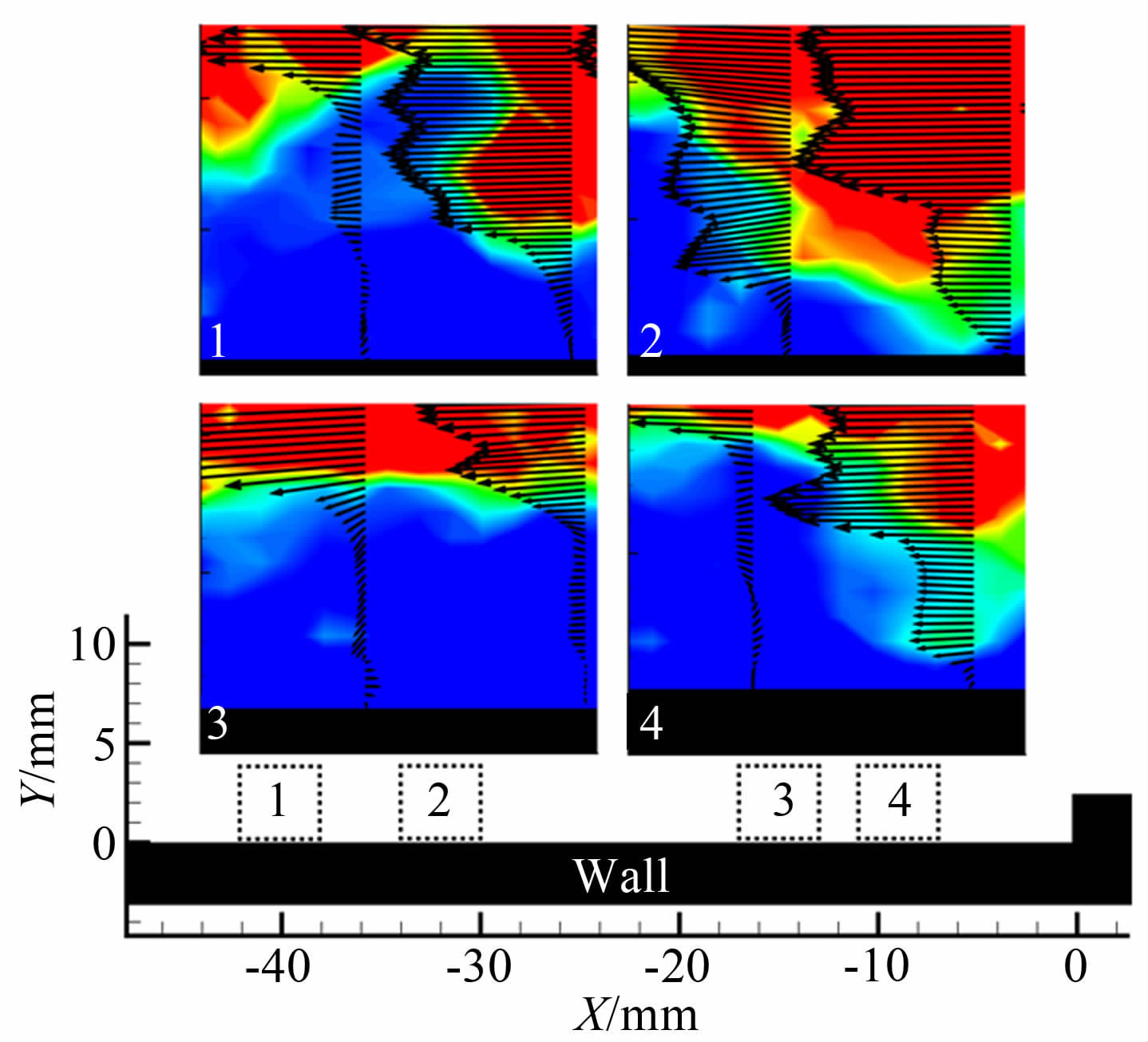
实验结果如图 25所示,其中图 25(a)、(b)分别表示y-z平面、x-y平面的测试结果。可见原始图片清晰,速度场符合客观规律,成功捕捉到了湍流边界层的精细结构,其中的绿色虚线为通过原始图片判断的湍流边界层轮廓。而图 26则更加清晰地反映了不同位置处的湍流边界层内的速度矢量:沿着流动方向分别取了4个位置放大显示,其中的位置编号与速度矢量图的编号一一对应。课题组下一步的工作将继续集中在优化粒子布撒效果及超声速环境中微小尺度湍流结构的观察上,并最终实现超声速燃烧流场的PIV测试。

|
| 图 25 Ma=4 平板PIV原始图片及速度云图 Fig. 25 Original pictures and the velocity contour of a Ma=4 plate |
|
| 图 26 Ma=4 平板PIV速度向量图 Fig. 26 Velocity contours of the Ma=4 plate |
超声速流场由于高滞止参数和存在强速度梯度区域,对粒子布撒器和示踪粒子的特性提出了更高的要求。通过跟随性模型分析现有粒子,可以发现受制于粒子的密度和粒径,激波波面附近粒子不能迅速地跟随气态介质改变速度,因此在速度梯度或者湍流强度大的区域,PIV的测量结果往往不能令人满意。即便模型能够准确判断密度和粒径已知的示踪粒子的跟随性,但是对于纳米粒子来说,要做到密度和粒径“已知”也是相当困难,这是因为:对于粒径,因为团聚等因素,固态粒子的真实粒径难以确定,而液态粒子从产生到测量的过程会发生冷凝或者蒸发,因此粒径也不能直接得到。至于密度,固态多孔材料的密度也只能粗略估计。另一方面,激波引起的气流密度的突变,会导致流场折射率的不一致,图 27就展示了激波波面附近模糊的视场[64],通过对比可以发现,区域B内由于激波的干扰使得画面失真,对速度场的计算极为不利。再者,文献[16]已经成功地将PIV技术应用到了Ma=7流场的测试中,而对于更高速度的流场测试,现有的PIV理论和技术能否适用还有待验证。
3.1.2 PIV系统本身的限制提高速度测量的精度和空间分辨率是PIV技术一直追求的2个关键之处,从原理上来讲,上述两者是相互制约的。时间间隔为Δt的2帧图像的速度测量误差和空间分辨率取决于视场的线性尺度lx和判读区内粒子可允许的最大位移Δxp,max,那么分别定义动态空间范围(Dynamic Spatial Range,DSR)和动态速度范围(Dynamic Velocity Range,DVR)[1]:
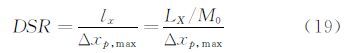
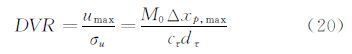
其中M0是图像放大率,LX(=lx M0)是图像传感器的线性尺度,umax(=Δxp,max /Δt)是判读区内粒子的最大速度,cτdτ(=σu Δt)是针对特定粒子图像直径(particle image diameter)dτ的最小可分辨粒子图像位移,cτ是一个关于判读算法的无量纲量,典型值在0.05到0.2之间。根据公式(19)和公式(20),我们可以得到
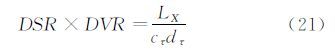
该不确定度原则表明,针对特定的PIV系统,动态空间范围和动态速度范围的乘积为常数。因此,如果提高空间分辨率,势必会降低相对测量精度。而目前所有的双脉冲PIV系统的DVR和DSR分别被限制在了200和100以下[1]。
3.1.3 特殊流场中示踪粒子的选择在航空发动机燃烧室的流场测试中,由于强旋涡流动和燃烧的存在,PIV技术的应用相当困难。目前常用示踪粒子的密度远大于气流的密度,受到旋涡气流离心力的影响,示踪粒子往往被“甩”出了旋涡的核心区域,因此得不到研究者们所关心的测试区域的速度场。而在燃烧场的测试中,对示踪粒子的要求则更加苛刻:首先需要保证示踪粒子不发生化学反应,再者,不能在高温环境下熔化,在此基础上,还必须有良好的散射特性,保证高的信噪比。公开文献中关于燃烧场PIV测量的报道不多,示踪粒子依然集中在了常用的固态粒子SiO2[8, 13]、Al2O3[58, 59]和TiO2上,如表 2所示。
| 材料 | 粒径/μm | 密度/(103 kg/m3) | 描述 |
| Al2O3 | 0.2~1 | 3.95~4.1 | 易聚团,高熔点2300K |
| SiO2 | 0.2~1 | 2.65 | 粒子分布均匀,散射性最好;熔点1900K |
| TiO2 | 0.01~1 | 4.23 | 粒子散射性好,2800K保持稳定;粒子分布不均匀 |
高精度、高分辨率始终是PIV技术的发展方向,通过上文的分析可知,精度和分辨率是相互制约的,因此在提升PIV系统中单体部件性能的同时,如何做好优化使得PIV系统整体性能得到最大的发挥至关重要。
通用的精确的PIV方法并不存在,必须从具体研究的流动机理角度改造相应的PIV测试手段,随着研究者们对复杂流场认知能力的不断提高,利用PIV技术更加深入地去揭示未知流动环境的愿望也更加迫切,因此深入以问题细致的需求驱动发展更加专用的体视PIV、全息PIV、显微PIV等专项PIV技术将成为今后的重点。超燃冲压发动机的研究热潮必然会将PIV测试技术提升到更高的层次。
超声速复杂流动中PIV测量的难点还是集中在粒子种类选择及布撒技术[65],同时与粒子特性相对应的光学特性也是研究薄弱的环节。自PIV技术诞生至今,示踪粒子的发展可以说始终处于停滞状态,目前的纳米级金属氧化物粒子包括液态粒子在高速复杂流场的测试中始终存在跟随性、信噪比等问题,因此急需寻找新型示踪粒子,使之能够适用于旋涡流、燃烧流场等极端流动环境。同时,粒子布撒技术也要突破现有结构的束缚。
4 结论及展望基于笔者所在课题组在超声速流场PIV技术领域的研究实践,针对示踪粒子布撒器设计,粒子松弛特性模型构建,激波流场测试分析,超声速平板湍流边界层结构分析等方面具体问题的研究和认识,从理论、定量化的角度深入分析了应用于超声速流场PIV技术现阶段依然存在的问题。根据我们的实践经验可以看出:在超声速流场中通用的精确的PIV方法不存在,必须从具体研究的流动机理角度改造相应的PIV测试手段。
超声速湍流边界层微细结构观察、超声速射流剪切层内小尺度混合研究都是目前超声速燃烧场的PIV测量的难题,目前超声速流场测试的PIV方法仍需要进一步发展。
通过不断深入的复杂流场机理研究及相应PIV方法研究,粒子图像测速方法的理论逐渐健全起来。今后大力推动精确PIV方法发展的责任主体一定是从事具体研究的流动机理的科学家,只有不断全面改造能够适应流动机理的PIV测试手段,才能更好的完成流动机理研究。
致谢:感谢国家自然基金委“面向发动机的湍流燃烧基础研究”重大研究计划项目(项目编号:91441205)、“高性能科学计算的基础算法与可计算建模” 重大研究计划项目(项目编号:91330203)支持。
| [1] | Westerweel J, Elsinga G E, Adrian R J. Particle image velocimetry for complex and turbulent flows[J]. Annual Review of Fluid Mechanics, 2013, 45:409-436. |
| [2] | Cameron S M, Nikora V I, Albayrak I, et al. Interactions between aquatic plants and turbulent flow:a field study using stereoscopic PIV[J]. Journal of Fluid Mechanics, 2013, 732:345-372. |
| [3] | Elsinga G E, Adrian R J, Van Oudheusden B W, et al. Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer[J]. Journal of Fluid Mechanics, 2010, 644:35-60. |
| [4] | Vennemann P, Kiger K T, Lindken R, et al. In vivo micro particle image velocimetry measurements of blood-plasma in the embryonic avian heart[J]. Journal of Biomechanics, 2006, 39(7):1191-1200. |
| [5] | Adrian R J. Twenty years of particle image velocimetry[J]. Experiments in Fluids, 2005, 39(2):159-169. |
| [6] | Adrian R J, Westerweel J. Particle image velocimetry[M]. Cambridge University Press, 2011. |
| [7] | Scarano F, Haertig J. Application of non-isotropic resolution PIV in supersonic and hypersonic flows[C]//5th International Symposium on Particle Image Velocimetry, Busan, Korea. 2003. |
| [8] | Scheel F. PIV measurement of a 3-dimensional reacting flow in a Scramjet combustion chamber[R]. AIAA-2004-1038. |
| [9] | Grant I. Particle image velocimetry:a review[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 1997, 211(1):55-76. |
| [10] | Elsinga G E, Van Oudheusden B W, Scarano F. Evaluation of aero-optical distortion effects in PIV[J]. Experiments in Fluids, 2005, 39(2):246-256. |
| [11] | Durst F, Melling A, Whitelaw J H. 激光多普勒测速技术的原理和实践[M]. 北京:科学出版社, 1992. Durst F, Melling A, Whitelaw J H. Principles and Practice of Lasser-Doppler Anemometry[M]. Beijing:Academic Press, 1992. |
| [12] | Kirmse T, Agocs J, Schröder A, et al. Application of particle image velocimetry and the background-oriented schlieren technique in the high-enthalpy shock tunnel Göttingen[J]. Shock Waves, 2011, 21(3):233-241. |
| [13] | Weisgerber H, Martinuzzi R, Brummund U, et al. PIV measurements in a Mach 2 hydrogen-air supersonic combustion[R]. AIAA-2001-1757. |
| [14] | Haertig J, Havermann M, Rey C, et al. Particle image velocimetry in Mach 3.5 and 4.5 shock-tunnel flows[J]. AIAA Journal, 2002, 40(6):1056-1060. |
| [15] | Scarano F, Van Oudheusden B W. Planar velocity measurements of a two-dimensional compressible wake[J]. Experiments in Fluids, 2003, 34(3):430-441. |
| [16] | Schrijer F F J, Scarano F, Van Oudheusden B W. Application of PIV in a Mach 7 double-ramp flow[J]. Experiments in Fluids, 2006, 41(2):353-363. |
| [17] | Koike S, Takahashi H, Tanaka K, et al. Correction method for particle velocimetry data based on the Stokes drag law[J]. AIAA Journal, 2007, 45(11):2770-2777. |
| [18] | Havermann M, Haertig J, Rey C, et al. PIV measurements in shock tunnels and shock tubes[M]//Particle Image Velocimetry. Berlin Heidelberg:Springer, 2008:429-443. |
| [19] | Wagner J L, Yuceil K B, Clemens N T. Velocimetry measurements of unstart of an inlet-isolator model in Mach 5 flow[J]. AIAA Journal, 2010, 48(9):1875-1888. |
| [20] | He L, Yi S H, Zhao Y X, et al. Experimental study of a supersonic turbulent boundary layer using PIV[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(9):1702-1709. |
| [21] | Hartmann A, Klaas M, Schröder W. Time-resolved stereo PIV measurements of shock-boundary layer interaction on a supercritical airfoil[J]. Experiments in Fluids, 2012, 52(3):591-604. |
| [22] | Sartor F, Losfeld G, Bur R. PIV study on a shock-induced separation in a transonic flow[J]. Experiments in Fluids, 2012, 53(3):815-827. |
| [23] | Davis T, Kumar R, Alvi F. Shear layer characteristics of supersonic free and impinging jets[J]. Shock Waves, 2014, 1:33. |
| [24] | Kompenhans J, Reichmuth J. Particle imaging velocimetry in a low turbulent windtunnel and other flow facilities[C]//AGARD conference proceedings. AGARD, 1986(399):35.1-35.13. |
| [25] | Reuss D L, Adrian R J, Landreth C C, et al. Instantaneous planar measurements of velocity and large-scale vorticity and strain rate in an engine using particle-image velocimetry[R]. SAE Technical Paper, 1989. |
| [26] | Muniz L, Martinez R E, Mungal M G. Applications of PIV to turbulent reacting flows[C]//Proc 8th Int Symp on Applications of Laser Techniques to Fluid Mechanics, Lisbon. 1996. |
| [27] | Anderson D J, Greated C A, Jones J D C, et al. Fibre optic PIV studies in an industrial combustor[C]//Proc 8th Int Symp on Applications of Laser Techniques to Fluid Mechanics, Lisbon. 1996. |
| [28] | 钟强, 陈启刚, 王兴奎, 等. 提高PIV片光源质量的研究[J]. 实验力学, 2013, 28(6):692-698. Zhong Qiang, Chen Qigang, Wang Xingkui, et al. On the improvement of PIV light sheet quality[J]. Journal of Experimental Mechanics,2013, 28(6):692-698. |
| [29] | Urban W D, Mungal M G. Planar velocity measurements in compressible mixing layers[J]. Journal of Fluid Mechanics, 2001, 431:189-222. |
| [30] | Ragni D, Schrijer F, Van Oudheusden B W, et al. Particle tracer response across shocks measured by PIV[J]. Experiments in Fluids, 2011, 50(1):53-64. |
| [31] | Huffman R, Elliott G. An experimental investigation of accurate particle tracking in supersonic, rarefied axisymmetric jets[R]. AIAA-2009-1265. |
| [32] | Schrijer F F J, Scarano F. Particle slip compensation in steady compressible flows[C]//7th International Symposium on Particle Image Velocimetry, Rome, Italy. 2007. |
| [33] | Melling A. Tracer particles and seeding for particle image velocimetry[J]. Measurement Science and Technology, 1997, 8(12):1406-1416. |
| [34] | Dring R P. Sizing criteria for laser anemometry particles[J]. Journal of Fluids Engineering, 1982, 104(1):15-17. |
| [35] | Tedeschi G, Gouin H, Elena M. Motion of tracer particles in supersonic flows[J]. Experiments in Fluids, 1999, 26(4):288-296. |
| [36] | Amatucci V A, Dutton J C, Kuntz D W, et al. Two-stream, supersonic, wake flowfield behind a thick base. I-General features[J]. AIAA Journal, 1992, 30(8):2039-2046. |
| [37] | Ghaemi S, Schmidt-Ott A, Scarano F. Nanostructured tracers for laser-based diagnostics in high-speed flows[J]. Measurement Science and Technology, 2010, 21(10):105403. |
| [38] | Chen F, Liu H, Rong Z. Development and application of nanoparticle tracers for PIV in supersonic and hypersonic flows[R]. AIAA-2012-0036. |
| [39] | Wooldridge J. Introductory econometrics:A modern approach[M]. Cengage Learning, 2012. |
| [40] | Stokes G G. On the effect of the internal friction of fluids on the motion of pendulums[M]. Pitt Press, 1851. |
| [41] | Loth E. Compressibility and rarefaction effects on drag of a spherical particle[J]. AIAA Journal, 2008, 46(9):2219-2228. |
| [42] | 徐惊雷. PIV技术在超及高超声速流场测量中的研究进展[J]. 力学进展, 2012, 42(1):81-90. Xu Jinglei. The development of the PIV experimental study of the super/hypersonic flowfield[J]. Advances in Mechanics, 2012, 42(1):81-90. |
| [43] | 张亚, 陈方, 刘洪, 等. 高速流动中PIV示踪粒子松弛特性研究[J]. 实验流体力学, 2013, 27(6):70-75. Zhang Ya, Chen Fang, Liu Hong, et al, Research on the relaxation characteristics of PIV tracer particles in supersonic flow[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6):70-75. |
| [44] | Urban W D, Mungal M G. Planar velocity measurements in compressible mixing layers[R]. AIAA-1997-075. |
| [45] | Goyne C P, McDaniel J C, Krauss R H, et al. Velocity measurement in a dual-mode supersonic combustor using particle image velocimetry[J]. AIAA Journal, 2001, 1761:24-27. |
| [46] | Kähler C J, Sammler B, Kompenhans J. Generation and control of tracer particles for optical flow investigations in air[M]//Particle image velocimetry:Recent improvements. Berlin Heidelberg:Springer, 2004:417-426. |
| [47] | Murakami M. Effect of tracer particles-quantized vortices interaction on PIV measurement result[C]//Advances in Cryogenic Engineering:Transactions of the Cryogenic Engineering Conference-CEC. AIP Publishing, 2014, 1573(1):300-306. |
| [48] | Arakeri J H, Das D, Krothapalli A, et al. Vortex ring formation at the open end of a shock tube:A particle image velocimetry study[J]. Physics of Fluids, 2004, 16(4):1008-1019. |
| [49] | Ganapathisubramani B, Clemens N T, Dolling D S. Large-scale motions in a supersonic turbulent boundary layer[J]. Journal of Fluid Mechanics, 2006, 556:271-282. |
| [50] | Ganapathisubramani B. Statistical properties of streamwise velocity in a supersonic turbulent boundary layer[J]. Physics of Fluids, 2007, 19(9):098108. |
| [51] | Theunissen R, Schrijer F F J, Scarano F, et al. Application of adaptive PIV interrogation in a hypersonic flow[C]//Proceedings of the 13th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, 2006:26-29. |
| [52] | Giepman R H M, Schrijer F F J, Van Oudheusden B W. Flow control of an oblique shock wave reflection with micro-ramp vortex generators:Effects of location and size[J]. Physics of Fluids, 2014, 26(6):066101. |
| [53] | Scarano F. Tomographic PIV:principles and practice[J]. Measurement Science and Technology, 2013, 24(1):012001. |
| [54] | Humble R A, Elsinga G E, Scarano F, et al. Investigation of the instantaneous 3D flow organization of a shock wave/turbulent boundary layer interaction using tomographic PIV[R]. AIAA-2007-4112. |
| [55] | Humble R A, Elsinga G E, Scarano F, et al. Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2009, 622:33-62. |
| [56] | Sun Z, Schrijer F F J, Scarano F, et al. The three-dimensional flow organization past a micro-ramp in a supersonic boundary layer[J]. Physics of Fluids, 2012, 24(5):055105. |
| [57] | Yamauchi H, Choi B, Takae K, et al. Flowfield characteristics of a transverse jet into supersonic flow with pseudo-shock wave[J]. Shock Waves, 2012, 22(6):533-545. |
| [58] | Narayanaswamy V, Clemens N T. Simultaneous LII and PIV measurements in the soot formation region of turbulent non-premixed jet flames[J]. Proceedings of the Combustion Institute, 2013, 34(1):1455-1463. |
| [59] | Buxton O R H, Burns R A, Clemens N T. Simultaneous Krypton PLIF, LII and PIV Measurements in a Sooting Jet Flame[C]//51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2013. |
| [60] | 全鹏程, 易仕和, 武宇, 等. 激波与层流/湍流边界层相互作用实验研究[J]. 物理学报, 2014, 63(8):084703. Quan Pengcheng, Yi Shihe, Wu Yu, et al. Experimental investigation of interactions between laminar or turbulent boundary layer and shock wave[J]. Acta Physica Sinica, 2014, 63(8):084703. |
| [61] | 荣臻, 陈方, 刘洪, 等. 粒子图像测速技术在马赫数4.0流场测试中的应用[J]. 实验流体力学,2012, 26(3):53-58. Rong Zhen, Chen Fang, Liu Hong, et al. Application of particle image velocimetry to Mach 4.0 flows[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3):53-58. |
| [62] | 荣臻, 陈方, 刘洪, 等. 超声速PIV示踪粒子布撒技术研究[J]. 实验流体力学, 2012, 26(2):64-67. Rong Zhen, Chen Fang, Liu Hong, et al. Research on seeding technique of PIV in supersonic flow[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(2):64-67. |
| [63] | Rong Z, Liu H, Chen F. Development and application of PIV in supersonic flows[C]//Recent Progresses in Fluid Dynamics Research:Proceeding of the Sixth International Conference on Fluid Mechanics. AIP Publishing, 2011, 1376(1):187-189. |
| [64] | Scarano F. Overview of PIV in supersonic flows[M]//Particle Image Velocimetry. Berlin Heidelberg:Springer, 2008:445-463. |
| [65] | Crosswy F L. Particle size distributions of several commonly used seeding aerosols[C]//Wind Tunnel Seeding Systems for Laser Velocimeters. 1985, 1:53-75. |
| [66] | Humble R A, Scarano F, Van Oudheusden B W. Particle image velocimetry measurements of a shock wave/turbulent boundary layer interaction[J]. Experiments in Fluids, 2007, 43(2-3):173-183. |
| [67] | Mathijssen T, Bannink W J, Scarano F. Investigation of a sharp-edged delta wing in a supersonic flow using stereo PIV[R]. AIAA-2009-3896. |