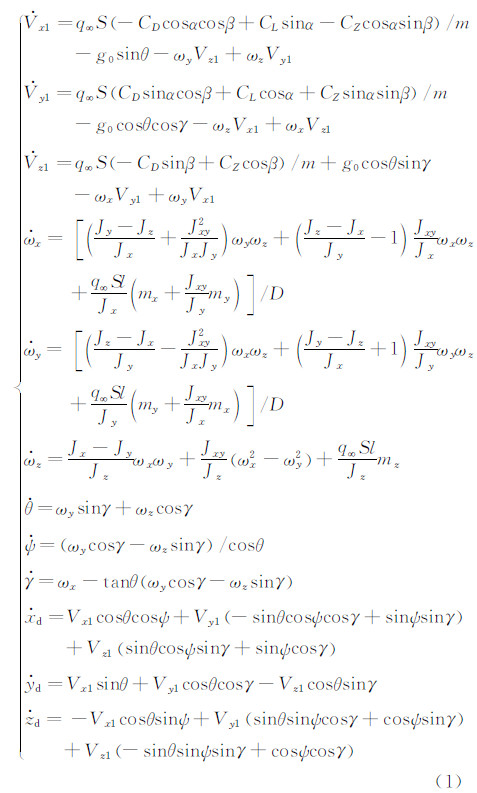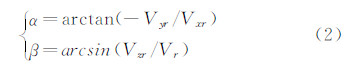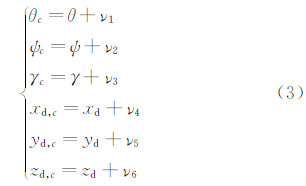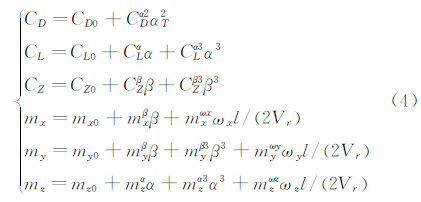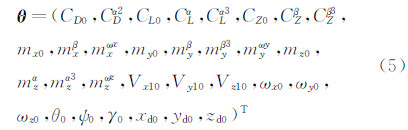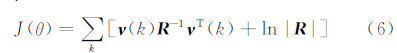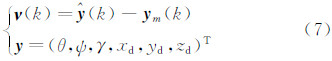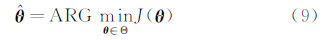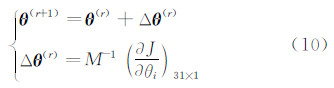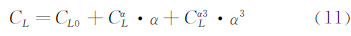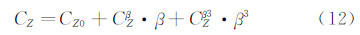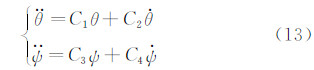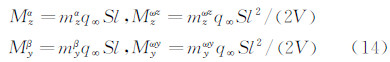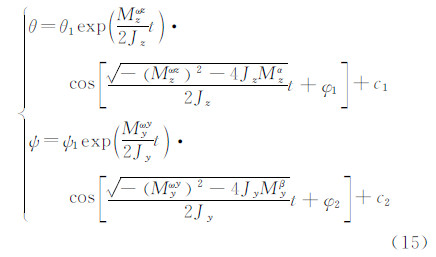2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Research Institute, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
在国内,目前气动力参数的获取主要基于常规风洞试验,飞行力学特性数据主 要基于大气自由飞试验[1]。风洞自由飞试验作为由常规风洞试验到全尺寸飞行器试飞试验之间的一个重要过渡环节,综合了以上两种试验手段,其拍摄记录了飞行器模型在风洞流 场中“自由飞行”的运动轨迹,既避免了风洞试验中模 型支撑装置对流场和气动参数测量结果的影响,又具有可控性、可重复性、费用低、周期短等优势。因此,风洞自由飞试验有利于获取飞行器气动力参数和飞行力学特性数据库,开展有关飞行器系统辨识的研究[2]。
由于风洞自由飞试验技术在现代先进飞行器设计中的重要作用,欧美日等相关大学和研究机构均在开展有关该试验技术的研究。德国亚琛工业大 学(RWTH Aachen University)自2008年起开展了利用风洞自由飞实现飞行器系统辨识的研究[3];日本东海大学、九州大学自2000年起开展了利用风洞自由飞实现飞行器飞行力学特性研究[4, 5, 6];目前,我国也在该领域开展了相关研究工作,文献[7]对有翼飞行器在脉冲风洞中自由飞试验的动导数测量结果进行了初步讨论;文献[8]讨论了风洞自由飞实验结果精准度的考 核标准;中国空气动力研究与发展中心蔡金狮等人[9]自1995年起开展了利用最大似然法对弹道靶自由飞试验进行气动参数辨识的研究。近年来,该中心正致力于风洞自由飞试验手段的各项研究工作[10]。
风洞自由飞试验测量数据中只包含模型位置和姿态角信息,无法获取线加速度、角速率及角加速度的测量量,若对有限的含噪声的位置和姿态角数据进行二阶数值微分,将造成气动系数的严重误差。因此,本文将气动参数辨识技术应用于风洞自由飞试验,利用有限测量数据(xd,yd,zd,θ,ψ,γ)获取飞行器的气动特性,并对此类试验提出几点建议,以提高气动参数辨识结果的可信度。
1 风洞自由飞试验气动力参数辨识原理及方法 1.1 气动力参数辨识基本原理目前工程上应用最为广泛的气动力参数辨识方法是最大似然法(MLE:Maximum Likelihood Estimation),该方法将参数辨识问题转化为一优化问题,通过优化选取气动力模型参数值,使模型输出与实测值间的偏差达极小[11]。对于风洞自由飞试验,图 1给出了气动参数辨识最大似然法的基本原理。
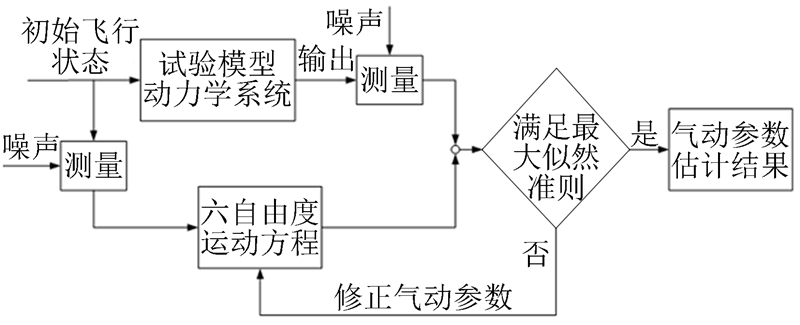 |
| 图 1 飞行器气动参数辨识最大似然法的基本原理 Fig 1 MLE for aircraft aerodynamic parameter estimation |
下文针对风洞自由飞试验,给出气动参数辨识最大似然法的数学模型、辨识准则、辨识算法以及辨识准度评价方法。
1.2 气动力参数辨识数学模型风洞自由飞试验气动力参数辨识问题的数学模 型由状态方程、观测方程、气动力模型构成。飞行器 六自由度动力学系统包括3个速度分量、3个角速率分量、3个欧拉角和3个位置坐标,共12个状态变量。参照航天工业标准QJ1028A中的弹体坐标系定义,原点o为模型质心,ox1轴沿模型纵轴,指向锥顶;oy1轴在纵对称平面内,垂直于ox1轴,向上为正;z轴垂直于ox1y1平面,其方向按右手定则确定。状态方程可如下:
式中:D=1-Jxy2/(JxJy);Vx1,Vy1,Vz1为体轴系速度分量;ωx,ωy,ωz为体轴系角速率分量;θ,ψ,γ为俯仰、偏航和滚转姿态角;xd,yd,zd为大地系位置坐标分量;m为飞行器质量;g0为重力加速度,取为常值;S为参考面积,l为参考长度;Jx,Jy,Jz,Jxy为惯性矩和惯性积;CD,CL,CZ,mx,my,mz为速度系下气动力和力矩系数;q∞为动压,q∞=1/2ρVr2,其中 V r 为相对 速度,由模型速度 V 与来流风速 V w合成,V r= V - V w;α,β分别为迎角和侧滑角,其计算公式如下:
观测向量取为 y =(θ,ψ,γ,xd,yd,zd)T,相应的观测方程为:式中:νi i=1,2,…,6 是观测噪声,为高斯白噪声。
在状态方程(1)中含有六分量气动系数。采用最大似然法进行气动参数辨识,需要给出参数化的空气动力数学模型。这里采用多项式模型,其中气动静导数取至3阶以反映非线性特性,动导数只取线性项。气动力系数的数学模型和相应气动参数的具体形式如下:
式中:αT为总迎角,
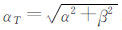 ;Cα·,Cα2·,Cα3·,Cβ·,Cβ3·,Cω·分别表示各气动力和力矩系数对迎角、总迎角二次方、迎角三次方、侧滑角、侧滑角三次方、角速率的气动导数。
;Cα·,Cα2·,Cα3·,Cβ·,Cβ3·,Cω·分别表示各气动力和力矩系数对迎角、总迎角二次方、迎角三次方、侧滑角、侧滑角三次方、角速率的气动导数。
气动力模型(4)所包含的气动参数均为待辨识参数。由于状态变量的初值是未知的,它对最大似然参数辨识结果的影响又较显著,通常将状态变量的初值也作为未知参数参加辨识。因此,待辨识参数为
1.3 气动力参数辨识准则及算法如1.1节所述,本文采用最大似然准则,其形式如下[12]:
式中, ν (k)为输出误差向量: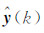 为由状态方程和观测方程计算得到的观测量预测值,y m(k)为观测量的实测值。 R 为观测噪声协方差矩阵,当观测噪声的统计特性未知时,采用 R 的最优估计:
为由状态方程和观测方程计算得到的观测量预测值,y m(k)为观测量的实测值。 R 为观测噪声协方差矩阵,当观测噪声的统计特性未知时,采用 R 的最优估计:
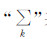 表示对辨识段所有数据点求和,N为辨识段数据点数。
表示对辨识段所有数据点求和,N为辨识段数据点数。
气动参数辨识问题就是寻求待辨识参数θ的最大似然估计值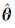 ,使准则函数J( θ )达最小值,即:
,使准则函数J( θ )达最小值,即:
本文采用修正Newton-Raphson迭代算法求解此优化问题。其迭代公式为:
式中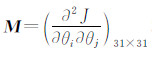 称为信息矩阵。
2 仿真辨识算例
2.1 仿真算例
称为信息矩阵。
2 仿真辨识算例
2.1 仿真算例
本节以某10°半锥角尖锥模型为例,具体说明气动力参数辨识算法在风洞自由飞试验中的应用。模型及试验工况的基本参数为:m=0.2217kg,l=0.16896m,底部直径D=0.06m,相对质心位置 cg=0.596,总压p0=514520Pa,总温T0=410K,来流马赫数Ma=5。
为验证算法的有效性,首先给定模型仿真初始条件,V=7m/s,θ=5°,ψ=5°,γ=0°,和1组气动力参数,由状态方程组(1)仿真得出各观测量的时间历程作为实测值。观测量取俯仰、偏航和滚转姿态角及3个位置坐标。选取以下14个气动参数进行辨识:CD0,Cα2D,CL0,CαL,CZ0,CβZ,mx0,mβx,my0,mβy,mωyy,mz0,mαz,mωzz。
主要气动力参数辨识值与真值(即仿真时用的参数值)的比较列于表 1,文中涉及到的角度单位采用弧度计。应用辨识所得参数对飞行器纵向位置坐标xd、法向位置坐标yd和迎角α进行估计,如图 2所示。由表 1和图 2可见,估计结果与仿真测量数据符合得较好,说明辨识结果是可信的。
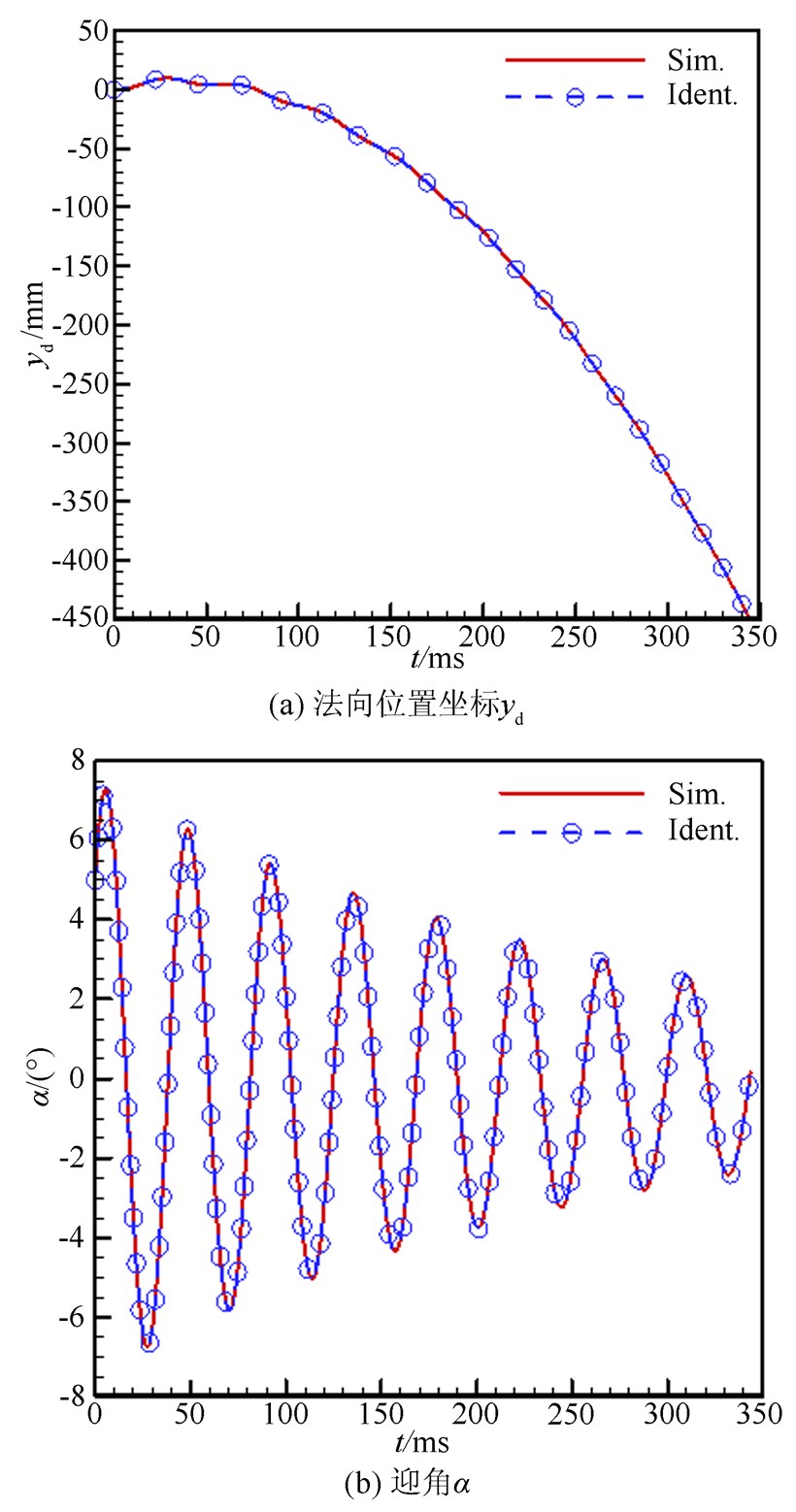 |
| 图 2 估计结果与仿真值的比较 Fig 2 Comparison of estimation and simulation |
在实际应用中,观测量的实测结果中不可避免地会存在测量噪声。将法向位置坐标的仿真计算结果分别叠加64组白噪声后作为测量值,此白噪声的标准差为对应测量值的1%,并计算辨识参数的平均值与标准差,列于表 1中。由表 1可见,法向位置坐标测量精度仅对法向气动参数影响较大,如零升系数CL0、升力线斜率CαL和动导数mωzz等,而对其它气动系数的辨识结果影响甚微,其中,零升系数和升力线 斜率的分布如图 3所示。由图 3可见,第4组试验 中,法向气动参数的辨识结果为CL0=-0.00072,CαL=5.10605,与真值偏差最大,但应用该组辨识结果对主要观测量进行拟合,其与测量值差异很小,如图 4所示。由此可见,法向位置坐标的测量准度对法向力气动系数的影响很大。
| 气动
参数 |
真值 | 辨识值 | |||
| Case1 | Case2 | Case3 | Case4 | ||
| CD0 | 0.13500 | 0.13500 | 0.13502 | 0.13506 | 0.13539 |
| σ(CD0) | - | - | 0.00002 | 0.00007 | 0.00053 |
| Cα2D | 2.57020 | 2.57020 | 2.56900 | 2.56574 | 2.54113 |
| σ(Cα2D) | - | - | 0.00158 | 0.00566 | 0.03859 |
| CL0 | 0.00000 | 0.00000 | -0.00013 | -0.00026 | -0.00072 |
| σ(CL0) | - | - | 0.00027 | 0.00050 | 0.00109 |
| CαL | 2.15624 | 2.15624 | 2.07060 | 1.78666 | 1.25394 |
| σ(CαL) | - | - | 1.11643 | 2.09025 | 5.73614 |
| CZ0 | 0.00000 | 0.00000 | -0.00003 | -0.00015 | -0.00045 |
| σ(CZ0) | - | - | 0.00045 | 0.00085 | 0.00230 |
| CβZ | -2.15624 | -2.15624 | -2.18416 | -2.24418 | -2.41409 |
| σ(CβZ) | - | - | 0.18697 | 0.35946 | 0.93932 |
| mx0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| σ(mx0) | - | - | 0.00000 | 0.00000 | 0.00000 |
| mβx | -0.01000 | -0.01000 | -0.01004 | -0.01013 | -0.01077 |
| σ(mβx) | - | - | 0.00006 | 0.00018 | 0.00095 |
| my0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| σ(my0) | - | - | 0.00000 | 0.00000 | 0.00000 |
| mβy | -0.16616 | -0.16616 | -0.16616 | -0.16616 | -0.16617 |
| σ(mβy) | - | - | 0.00000 | 0.00001 | 0.00003 |
| mωyy | -0.50000 | -0.50000 | -0.49979 | -0.49955 | -0.50361 |
| σ(mωyy) | - | - | 0.00345 | 0.00628 | 0.01897 |
| mz0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00001 |
| σ(mz0) | - | - | 0.00000 | 0.00000 | 0.00001 |
| mαz | -0.16616 | -0.16616 | -0.16614 | -0.16611 | -0.16577 |
| σ(mαz) | - | - | 0.00006 | 0.00011 | 0.00056 |
| mωzz | -0.50000 | -0.50000 | -0.50208 | -0.50872 | -0.52700 |
| σ(mωzz) | - | - | 0.02240 | 0.04219 | 0.11483 |
| 说明:Case1: 仿真值作为测量值; Case2: 仿真值yd叠加白噪声后作为测量值,信噪比为100∶1; Case3: 仿真值yd叠加白噪声后作为测量值,信噪比为100∶2; Case4: 仿真值yd叠加白噪声后作为测量值,信噪比为100∶5。 |
|||||
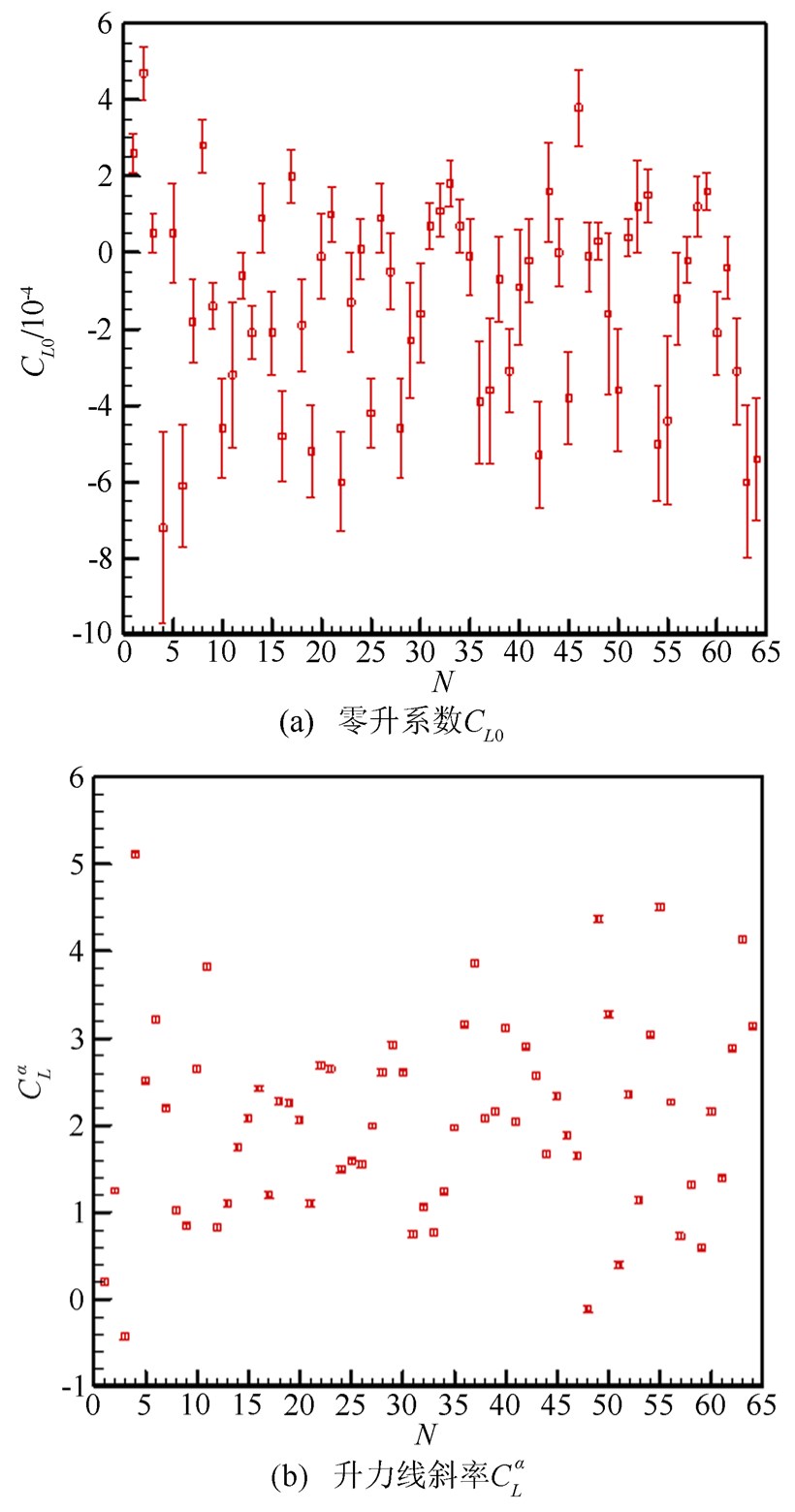 |
| 图 3 法向气动参数辨识结果 Fig 3 Identified results of the normal aerodynamic parameters |
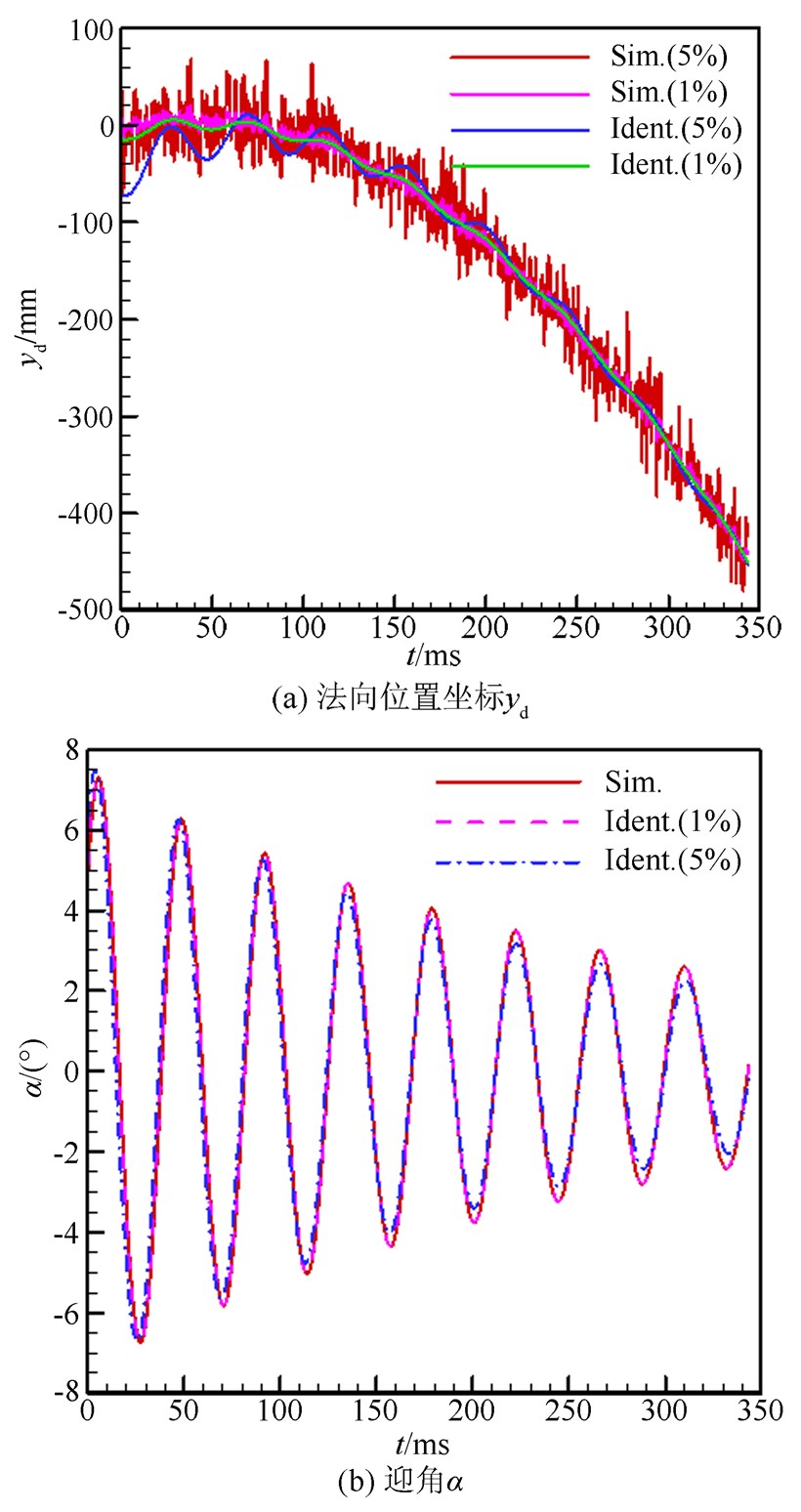 |
| 图 4 估计结果与仿真值的比较(含噪声) Fig 4 Comparison of estimation and simulation (with noise) |
为了进一步观察噪声对辨识结果的影响程度,加大噪声信号,将64组噪声幅值分别改为2%和5%叠加到法向位置坐标的仿真值中作为测量值,辨识结果同样列于表 1。由表 1可见,零升系数CL0、升力线斜率CαL及动导数mωzz等参数辨识结果误差进一步增大。在噪声幅值为1%、2%和5% 3种情况下,CαL的辨识误差分别为3.97%、17.14%和41.85%,动导数mωzz的辨识误差分别为0.42%、1.74%和5.4%。因此,为了保证CL0及CαL辨识结果的有效性,噪声幅值应控制在2%以内,即测量精度控制在10mm。在噪声幅值5%情况下,选取其中辨识结果与真值偏离最大的1组气动参数对观测量进行拟合,如图 4所示。由图 4可见,法向位置拟合结果与测量值偏差较大,与零升系数CL0与升力线斜率CαL的辨识结果较差有关。因此,法向位置坐标的测量精度会影响法向力系数的可信度。此外,由于CL0与CαL 2者均作用于升力系数,公式如下:
只要恰当组合CL0与CαL,亦可得到满意的升力系数。因此,小不对称量CL0对CαL影响很大。鉴于侧向位置坐标zd随侧滑角的变化也不明显,侧力系数也有类似公式: 因此,CZ0与CβZ可得到类似结论:侧向位置坐标的测量精度会影响侧向力系数的可信度,微小测量误差即会造成CZ0与CβZ的不可辨识,且CβZ的可辨识性受CZ0影响很大。因此,风洞自由飞试验中的气动参数CL0、CαL、CZ0与CβZ的辨识结果受观测量精度影响较大,对风洞自由飞试验中观测量的测量精度有较高要求,位置坐标的精度需控制在10mm以内。相对而言,动导数mωyy与mωzz受观测量精度影响较小,位置坐标的测量精度控制在25mm的合理范围内即可。实际上,由于力矩导数主要影响短周期运动,力导数影响长周期运动[13],而风洞自由飞试验的空间较小,试验时间较短,长周期运动体现不充分,位置坐标随迎角、侧滑角的变化不明显,因此,力导数的辨识存在一定难度。只有在模型上安装过载测量设备的情况下,风洞自由飞试验才能对力导数进行有效辨识。
3 实测数据辨识算例 3.1 实测数据算例上一节算例是将各观测量的仿真时间历程作为实测值,并未考虑到真实风洞试验环境下不可避免的传感器常值误差、传感器安装位置误差、传感器时间延长误差、测量噪声等一系列干扰的影响,即便对仿真值叠加白噪声也并不能完全反映真实试验飞行历程,所以本节针对10°半锥角尖锥模型的风洞自由飞试验实测数据开展气动力参数辨识研究。
试验是在中国空气动力研究与发展中心超高速空气动力研究所Φ1m高超声速风洞中进行的。试验工况、模型构型、观测量与待辨识气动参数的选取与2.1节一致。所得气动参数的辨识结果列于表 2。利用气动参数辨识结果对状态变量进行拟合,与实测数据的比较如图 5所示。
| 气动参数 | 辨识结果 | DATCOM结果 | 近似解析解 |
| CD0 | 0.19354 | - | - |
| Cα2D | 0.11889 | - | - |
| CL0 | -0.04001 | - | - |
| CαL | 2.28618 | 2.02827 | - |
| CZ0 | -0.03319 | - | - |
| CβZ | 1.34235 | -2.02827 | - |
| mx0 | 0.00012 | - | - |
| mβx | -0.00908 | 0.00000 | - |
| my0 | -0.00126 | - | - |
| mβy | -0.20601 | -0.14324 | -0.20433 |
| mωyy | -0.49813 | -0.22918 | -0.45308 |
| mz0 | 0.00366 | - | - |
| mαz | -0.19345 | -0.14324 | -0.20449 |
| mωzz | -0.28897 | -0.22918 | -0.38361 |
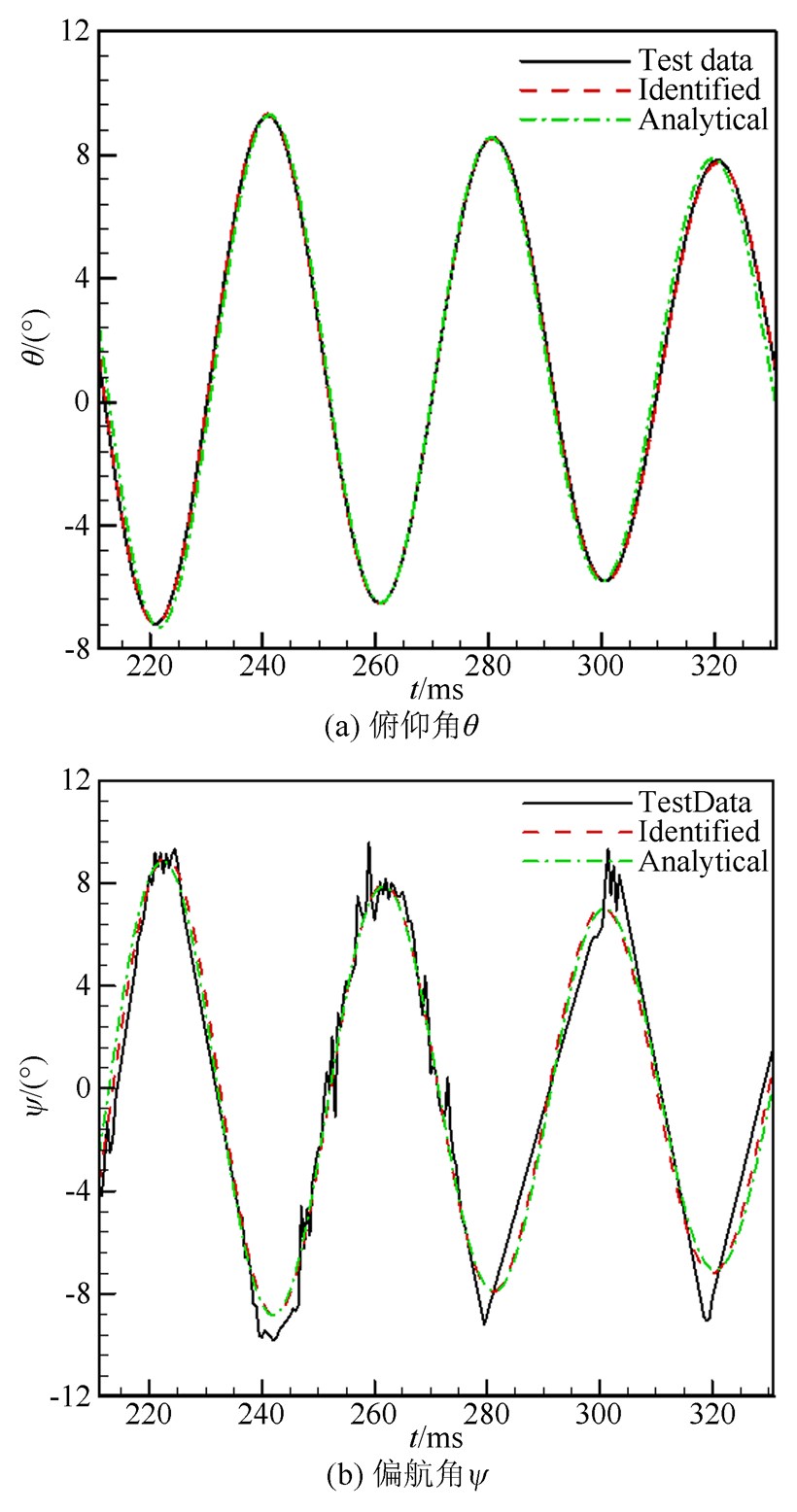 |
| 图 5 拟合结果与测量值的比较 Fig 5 Comparison of fitting results and measurement |
同时,本文给出了mβy、mαz、mωyy、mωzz等气动参数的近似解析解。考虑一种比较理想的简单情况,即在自旋速度很小时,对于轴对称模型,较为简单准确 的线性力学模型是俯仰角θ与偏航角ψ组成的常系数微分动力学方程组,公式如下[14]:
式中:由于模型为轴对称体,因此方程组(13)有解析解:
由方程组(14)出发,分别通过观测量 ti,θi i=0,1,…,n和 ti,ψi i=0,1,…,n,采用遗传算法(GA:Genetic Algorithms[15])识别出方程中mβy、mαz、mωyy、mωzz等气动参数和姿态角的拟合曲线,如表 2和图 5所示。图中,“Identified”和“Analytical”分别表示利用辨识结果和近似解析解得到的姿态角拟合曲线。此外,表 2中也列出部分气动参数近似牛顿解,由气动力工程计算软件DATCOM[16]得出。
3.2 结果分析综合比较表 2与图 5结果,下面对模型的气动参数辨识结果进行简要分析。
(1) 静导数mαz与mβy辨识结果近似相等,与DATCOM计算结果比较,相对误差分别为5.51%和28.41%,基本满足工程精度要求。造成mβy误差较大的主要原因是偏航角实测数据质量较差,如图 5(b)中偏航角多次出现尖点,对航向静导数辨识结果造成较大影响。
(2) 俯仰阻尼导数mωzz与DATCOM计算结果相比偏小26.09%,文献[17]、[18]中辨识结果也比近似牛顿解计算结果偏小。
(3) 偏航阻尼导数mωyy辨识结果比DATCOM计算结果偏小约1倍。造成大误差的原因主要有2方面:一方面,DATCOM等工程计算软件算法精度有限,下一步考虑开展计算流体力学研究,并应用其计算结果进行比对;另一方面,偏航角实测数据质量较差,且航向静导数误差已较大,进而对航向动导数辨识结果造成很大影响。
(4) 在不考虑模型自旋情况下,最大似然辨识方法与近似解析方法的理论基础相同,两者得到的气动参数结果一致。但当考虑模型自旋时,将计入模型进动和章动的影响,解析方法将成为三周期法,而最大似然辨识方法仅增加一个待辨识参数,方法仍适用。
(5) 利用气动参数辨识结果对姿态角进行拟合,与实测数据一致性较好,说明辨识结果具有一定可信度。 4 初步结论
通过仿真辨识算例和实际风洞试验辨识算例结果可得出以下初步结论:
(1) 静导数辨识结果mαz与mβy近似相等,且与DATCOM计算结果接近,动导数mωzz变化趋势与国外文献发表结果一致。说明将基于最大似然法的气动参数辨识技术应用于风洞自由飞试验中,是获取飞行器气动特性的有效途径之一。
(2) 位置坐标的测量误差将造成长周期气动参数CαL、CβZ等结果的可信度较低,甚至不可辨识。因此,可提高测量数据精准度(通过提高高速摄像设备的性能实现,如提升拍摄速度与增多像元素),如法向、侧向位置坐标的测量精度控制在10mm以内,有效提高参数辨识结果的可信度。
(3) 动导数mωyy与mωzz的可辨识性较高,观测量的测量精度控制在25mm的合理范围内即可。此外,在模型上安装过载测量设备,增加加速度等测量量,亦可提高待辨识气动参数的可信度。
| [1] | 张守言主编. 模型自由飞试验[M]. 北京: 国防工业出版社, 2002. |
| [2] | 卿理勋. 几种动态模型自由飞试验技术[J]. 飞行力学, 1995, 13(3): 18-23. |
| [3] | Jan N, Wolfgang A. Free flight wind tunnel tests for parameter identification[R]. RWTH Aachen University, 2008. |
| [4] | Yamasaki T, Fujita H, Goto N. Identification of blimp dynamics by indoor free flight tests[R]. AIAA 2002-4405. |
| [5] | Kikomoto Y, Kobayashi O. Free flight of airplane in wind tunnel[C]. Proceedings of Aircraft Symposium, 2000. |
| [6] | Sakata H, Kobayashi O. Free flight of airplane in wind tunnel (Second Report)[C]. Proceedings of Aircraft Symposium, 2003. |
| [7] | 马家驩, 李江, 潘文欣, 等. 有翼飞行器高超声速动导数的风洞自由飞测量[J]. 流体力学实验与测量, 2001, 15(4): 70-76. Ma Jiahuan, Li Jiang, Pan Wenxin, et al. Hypersonic pitching damp measurements for a winged vehicle by model free flight[J]. Experiments and Measurements in Fluid Mechanics, 2001, 15(4): 70-76. |
| [8] | 贾区耀, 杨益农, 蒋增辉. 风洞自由飞实验结果的精度、准度[J]. 宇航学报, 2009, 30(6): 2082-2085. Jia Quyao, Yang Yinong, Jiang Zenghui. The precision and accuracy of wind tunnel free-flight experiment result[J]. Journal of Astronautics, 2009, 30(6): 2082-2085. |
| [9] | 蔡金狮, 万宗国. 自由飞弹道靶气动参数辨识[C]//第7届跨声速流学术会议论文集, 1995: 72-77. |
| [10] | 孙海生, 岑飞, 聂博文, 等. 水平风洞模型自由飞试验技术研究现状及展望[J]. 实验流体力学, 2011, 25(4): 103-108. Sun Haisheng, Cen Fei, Nie Bowen, et al. Present research status and prospective application fo wind-tunnel free-flight test technique[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 103-108. |
| [11] | 蔡金狮, 汪清, 王文正, 等. 飞行器系统辨识学[M]. 北京: 国防工业出版社, 2003. |
| [12] | 汪清, 钱炜祺, 何开锋. 导弹气动参数辨识与优化输入设计[J]. 宇航学报, 2008, 29(3): 789-793. Wang Qing, Qian Weiqi, He Kaifeng. Aerodynamic paramenter identification and optimal input design for missile[J]. Journal of Astrinautics, 2008, 29(3): 789-793. |
| [13] | 顾均晓. 飞行稳定性和自动控制[M]. 北京: 国防工业出版社, 2008. |
| [14] | Eikenberry R S. Analysis of the angular motion of missiles[R]. SC-CR-70-6051, 1970. |
| [15] | 钱炜祺, 汪清, 王文正, 等. 遗传算法在气动力参数辨识中的应用[J]. 空气动力学学报, 2003, 21(2): 196-201. Qian Weiqi, Wang Qing, Wang Wenzheng, et al. Application of genetic algorithms for aerodynamic parameter estimation[J]. Acta Aerodynamica Sinica, 2003, 21(2): 196-201. |
| [16] | Auman L, Doyle J, Rosema C, et al. Missile Datcom user's manual[M]. 2008 revision. AFRL-RB-WP-TR-2009-3015, 2008. |
| [17] | Prislin R H. High amplitude dynamic stability characteristics of blunt 10-degree cones[R]. AIAA-66-0465. |
| [18] | 马家驩, 潘文欣, 翟曼玲, 等. 10°尖锥标模高超声速动导数的实验测量[J]. 空气动力学学报, 1997, 15(4): 452-456. Ma Jiahuan, Pan Wenxin, Zhai Manling, et al. 10° Cone model free flight experiment in hypersonic impulse type wind tunnel for dynamic stability measurement[J]. Acta Aerodynamica Sinica, 1997, 15(4): 452-456. |