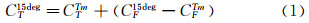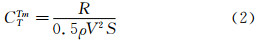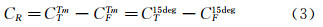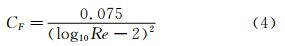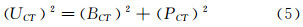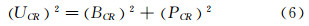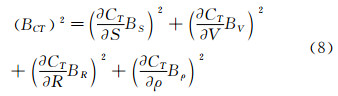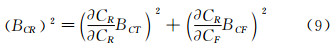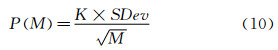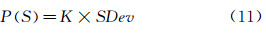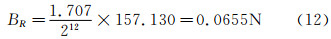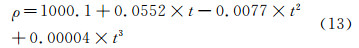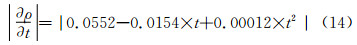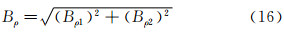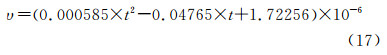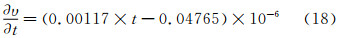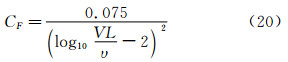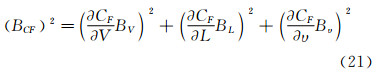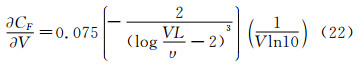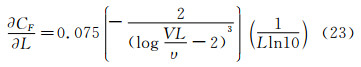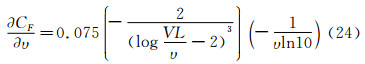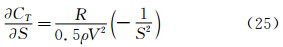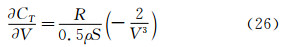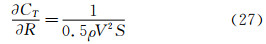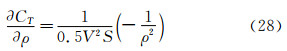2. 高速水动力航空科学技术重点实验室, 湖北 荆门 448035
2. Key Aviation Scientific and Technological Laboratory of High-speed Hydrodynamic, Jingmen Hubei 448035, China
在船舶领域,ITTC(国际船模拖曳水池会议)十分重视不确定度研究工作。1999~2002年ITTC形成了一套推荐的标准试验规程,对船舶基准试验,特别是水动力性能的模型试验提出了标准的试验程序、试验数据表达方法和试验结果不确定度分析方法[1, 2]。周广利[3, 4]和施奇[5]分别应用ITTC推荐规范进行了船模阻力试验测量不确定度分析研究。与风洞试验的不确定度分析原理相同[6, 7, 8],ITTC将不确定度中偏差极限和精密度极限分开计算,这样的分析思路很清晰,也便于理解,并且计算扩展不确定度时只将通过统计分析的精密度极限进行扩展[9]。本文参照ITTC推荐规程中试验流体动力学不确定度分析规范[10, 11, 12, 13],对该模型的摩擦阻力系数、总阻力系数进行了不确定度分析,分析了误差源,提出了减小潜艇模型阻力试验的测量不确定度的改进意见。
1 试验原理不确定度分析可以用来指明哪些测量或试验程序是造成不确定度水平的主要原因。这样通过改进与这些测量或试验过程有关的技术,就可以减少整个试验不确定度的水平。
1.1 试验设计潜艇标模阻力试验结果换算采用的是二因次法。通过测量阻力R、速度V和水温t以及测量湿表面积S和密度ρ或者直接应用它们的参考值,总阻力系数CT在名义温度15℃下可以这样计算:
其中:
因而剩余阻力系数CR可表示为:
公式(1)中阻力系数从测量模型温度(上标Tm)到名义温度15℃的变化值是按ITTC-1978预报方法得出的,而公式(1)中摩擦阻力系数CF是按ITTC-1957平板摩擦阻力公式计算出的:
其中:Re为不同温度下的雷诺数。
1.2 测量系统和步骤由偏差极限引起的总不确定度将由潜艇标模SUBOFF的几何外形、速度、阻力以及温度、密度和粘性这几个测量系统估算出。图 1列出了阻力试验的不确定度分析步骤。
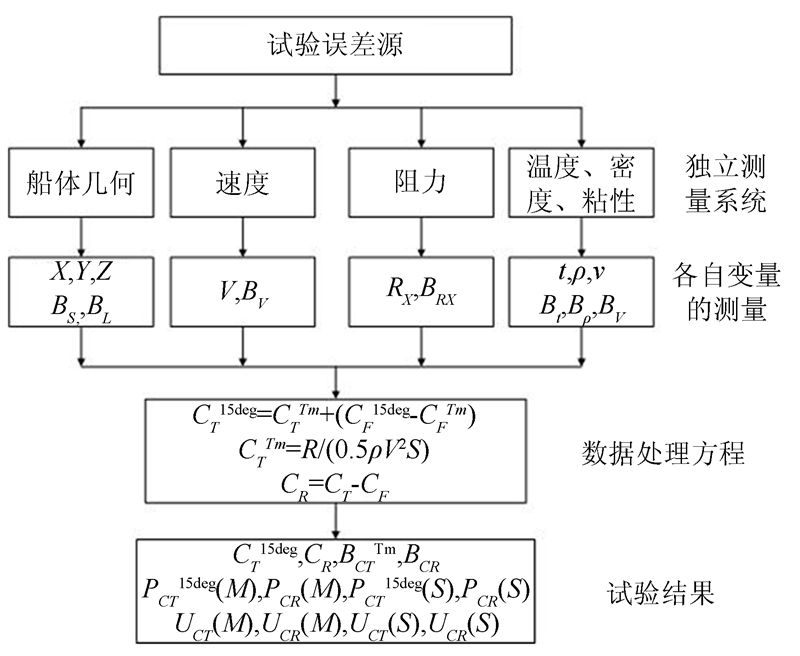 |
| 图 1 阻力试验的不确定度分析步骤图 Fig. 1 Flow chart of uncertainty analysis of resistance test |
由数据处理方程(2)和(3)可分别推出偏差极限BCTTm和BCR。当潜艇标模温度从测试温度到名义温度变化量较小的话,由转换公式(1)知,偏差极限可不予考虑。
在多点(m)和单点(s)试验工况下,总阻力系数在名义温度15°下的精密度极限PCT15deg和剩余阻力系数精密度极限PCR是由端-端法来估算的。
1.3 标模主尺度SUBOFF项目是由美国国防高等研究计划署(DARPA)提出的,SUBOFF 项目中的潜艇模型是由轴对称体和指挥台围壳、尾翼以及ring wings等附体组合而成,其目的就是为潜艇设计提供水动力与尾流场信息[14]。
SUBOFF项目的主艇体潜艇模型,即轴对称回转体的三维粘性绕流场进行试验。主尺度是表征潜艇外形大小的基本量度参数,是标志一艘潜艇大小的指标,也是潜艇设计计算和建造的依据[15]。表 1给出了潜艇标模SUBOFF主尺度。
| 名称 | 符号 | 数值(单位) |
| 艇体总长 | L | 4.356m |
| 进流段长 | 1.016m | |
| 平行舯体长 | 2.229m | |
| 去流段场 | 1.111m | |
| 最大直径 | 0.508m | |
| 排水质量 | 701.571kg | |
| 湿表面积 | S | 5.988m2 |
总阻力系数不确定度以方和根的形式给出总偏差极限和总精密度极限:
本试验忽略温度转换引起的测量数据的偏差极限(见公式(1)),所以可得:
总阻力系数的偏差极限BCT可由下式计算:
剩余阻力系数的偏差极限BCR可由下式计算:
由CT15deg和CR通过端-端法首先得出包含速度、阻力和温度、密度以及粘性的精密度误差,进而推出单次试验(s)和多次试验(m)平均值的精密度极限。不管是否确定单次或多次试验的精密度极限,都必须从多次试验中得出标准偏差。那么多次试验的精密度极限可按下式计算:
式中:M为决定精密度极限的试验次数;SDev为多次试验确定的标准偏差;K=2参照ITTC中不确定度评估方法给出。
单次试验精密度极限计算公式为:
2.1 偏差极限在下面每一组偏差(几何外形、速度、阻力和温度/密度/粘性)中,基本误差源可分为以下几类:标定误差;数据采集误差;数据处理误差和概念误差,以下不再赘述。
2.1.1 艇体几何外形(湿表面积)潜艇外形一般都是一个流线型体,表示其形状的最基本图形即为型线图[16]。潜艇标模SUBOFF是按几何相似的型线图来加工的。不管尽多大的努力,模型的制造过程也不可能是十全十美,因此潜艇标模SUBOFF在外形和湿表面积总存在着误差,不仅影响湿表面积,而且还影响着阻力的测量。
由于潜艇标模SUBOFF制造误差引起的湿表面积可由特别方法估算,根据ITTC01版规程7.5-01-01-01的假定,即模型误差在所有坐标点为±1mm,长度将增减2mm,湿表面积增加0.019m2或者减少0.029m2。由于潜艇标模SUBOFF外形的估计误差引起的长度偏差极限BL=0.002m,湿表面积偏差极限BS=0.029 m2。潜艇标模SUBOFF阻力试验是采取双剑测量方法,前后剑上均装有阻力传感器,潜艇标模SUBOFF受到的阻力为2个阻力传感器测量值之和,如图 2所示。
 |
| 图 2 潜艇标模SUBOFF阻力试验安装图 Fig. 2 Resistance test installation of submarine standard model SUBOFF |
拖车速度测量系统由1个固定在从动轮上的光学编码器、1个脉动计数器和1个用于数据采集的计算机组成。在拖车的从动轮上装有弹性装置,使该轮与拖车轨道的上表面保持接触,所以该轮是由拖车与轨道之间的相对运动来驱动的。从动轮的周长为500mm,轮轴与光学编码器相连。光学编码器沿圆周开了5000个等间距与大小的窗口。当编码器随从动轮转动时,脉动计数器计数经过窗口的数目[4]。而拖车数字式仪表显示的有效数字为±1mm,所以拖车速度测量系统的偏差主要是由数据截断引起的,BV=0.0005m/s。图 3为拖车左前方测速轮图,拖车速度就是测速轮通过光学偏码器获得的。
 |
| 图 3 拖车左前方测速轮图 Fig. 3 Measure wheel in left-front of towing truck |
阻力传感器直接安装在拖车上,只接受沿潜艇标模SUBOFF行进方向的负荷。阻力的主要误差源来自于阻力传感器的标定。阻力值需要通过模数转换得出,精度为12位的模数转换器的误差输出为1位。因此模数转换器的电压偏差极限为模数转换器误差乘上电压范围(-10~10V),然后除以精度得出。最后乘上标定曲线斜率值,把伏特值转换为牛顿值。图 4为阻力仪标定过程图,将阻力传感器垂直地面,悬挂标定砝码,测量得到电压。阻力传感器标定结果如表 2所示,对阻力传感器测量结果进行线性拟合,得到曲线斜率值为157.130,测量电压的标准差为1.707,则通过公式(12)可计算得到阻力的偏差极限。
| 输出/Volt | 质量/kg | 力/N |
| 0.000 | 0.0 | 0.000 |
| 0.313 | 5.0 | 49.050 |
| 0.625 | 10.0 | 98.100 |
| 0.936 | 15.0 | 147.150 |
| 1.247 | 20.0 | 196.200 |
| 1.874 | 30.0 | 294.300 |
| 2.497 | 40.0 | 392.400 |
| 2.809 | 45.0 | 441.450 |
| 3.120 | 50.0 | 490.500 |
| 3.743 | 60.0 | 588.600 |
| 4.057 | 65.0 | 637.650 |
| 4.371 | 70.0 | 686.700 |
| 4.682 | 75.0 | 735.750 |
| 4.997 | 80.0 | 784.800 |
| 其中:R=157.130×Volt+0.0273 | ||
如图 5所示,温度计为铂电阻测温系统,测量范围为-10~90℃,精度为0.10℃,因而由温度测量引起的偏差极限Bt=0.10℃。
根据ITTC 7.5-02-01-03,当g=9.81m/s2时,温度与密度的关系可表示为:
 |
| 图 4 阻力仪标定图 Fig. 4 Calibration of resistance instrument |
 |
| 图 5 铂电阻测温系统 Fig. 5 Platinum resistance thermometer |
密度对温度的灵敏度系数为:
当t=15℃,Bt=0.10℃时,偏差Bρ1由下式计算出:
根据ITTC-78方法,名义密度ρ=1000。由此引入一个偏差极限,为ρ(15℃)=999.34和ρ=1000相互之间的差值。即Bρ2=1000-999.345=0.655kg/m3。
此时密度总偏差极限为:
即Bρ=0.655kg/m3。
根据ITTC 7.5-02-01-03,粘性系数与温度在淡水中的关系为:
粘性系数对温度的灵敏度系数为:
当t=15℃,Bt=0.10℃时,偏差Bυ由下式计算:
即,Bυ=0.003×10-6m2/s。
2.1.5 摩擦阻力系数摩擦阻力系数是根据ITTC 1957摩擦阻力公式计算:
摩擦阻力计算的偏差可追溯到潜艇标模SUBOFF的长度、速度和粘性引起的误差。从而推出摩擦阻力系数的偏差极限为:
摩擦阻力系数对速度、长度、粘性的灵敏度系数为:
代入BV=0.0005m/s,BL=0.002m,Bυ=0.003×10-6m2/s,V=6.090m/s和8.230m/s。摩擦阻力偏差极限为CF=4.371×10-7和4.145×10-7。
由图 6可知摩擦阻力系数的不确定度传递中,由温度引起的运动粘性系数的偏差极限占到97%,且不随速度发生变化,准确的测量温度可以减少摩擦阻力系数的偏差极限。
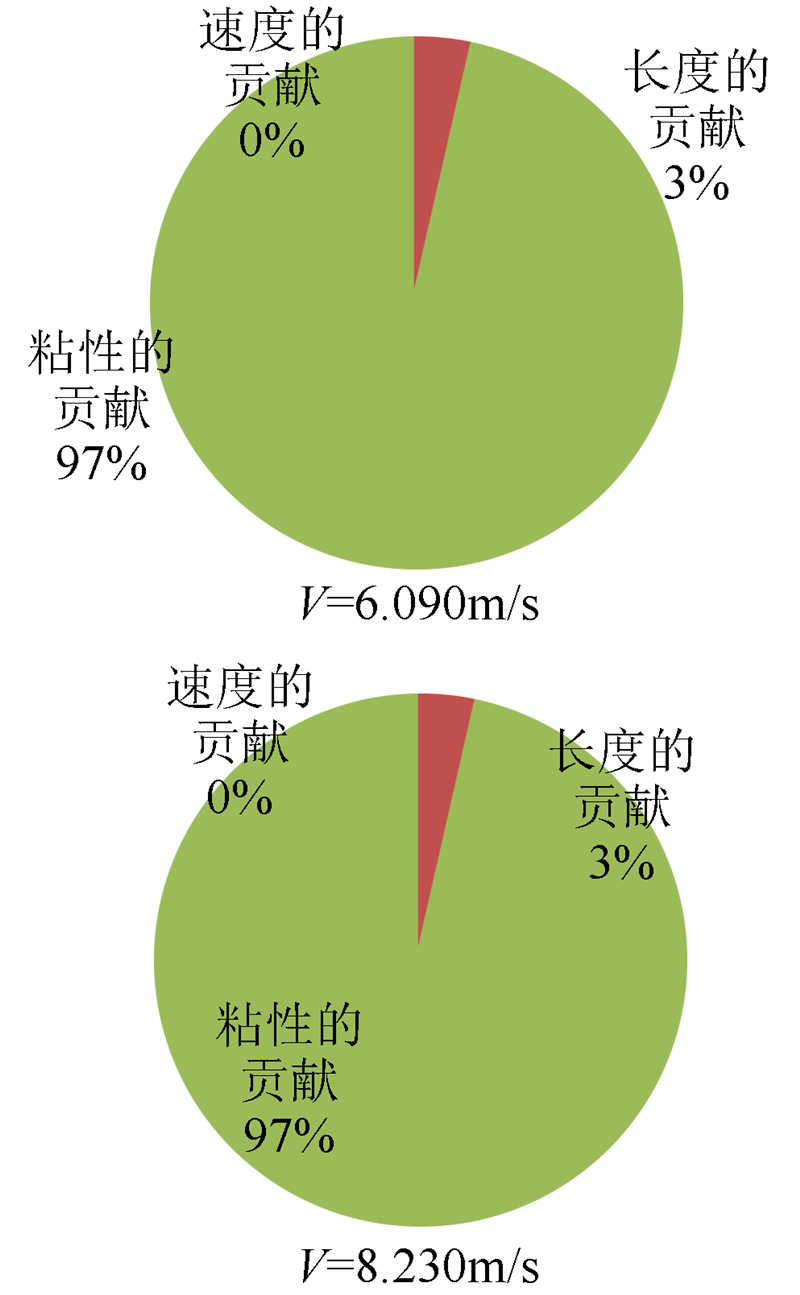 |
| 图 6 速度、长度、粘性偏差极限分量在摩擦阻力系数偏差极限中的贡献 Fig. 6 Contribution of velocity,length,kinematical viscosity bias limits to friction resistance coefficient bias limit |
为了计算总偏差极限和总精密度极限,必须计算以下几个灵敏度系数,R=361.173N和557.729N,g=9.81m2/s,S=5.988 m2,V=6.090m/s和8.230m/s。
根据公式(8),总阻力系数的偏差极限为BCT=1.591×10-5和1.345×10-5。
由图 7可知总阻力系数的偏差极限98%来自于湿表面积的偏差极限,且不随速度发生变化。
2.1.7 剩余阻力系数剩余阻力系数对总阻力系数和摩擦阻力系数的灵敏度系数:
根据公式(9),剩余阻力系数的偏差极限为BCR=1.592×10-5和1.345×10-5。
由图 8可知剩余阻力系数的偏差极限几乎100%来自于总阻力系数的偏差极限。而总阻力系数的偏差极限主要来自湿表面积,所以需提高模型的加工精度,降低湿表面积的偏差极限。
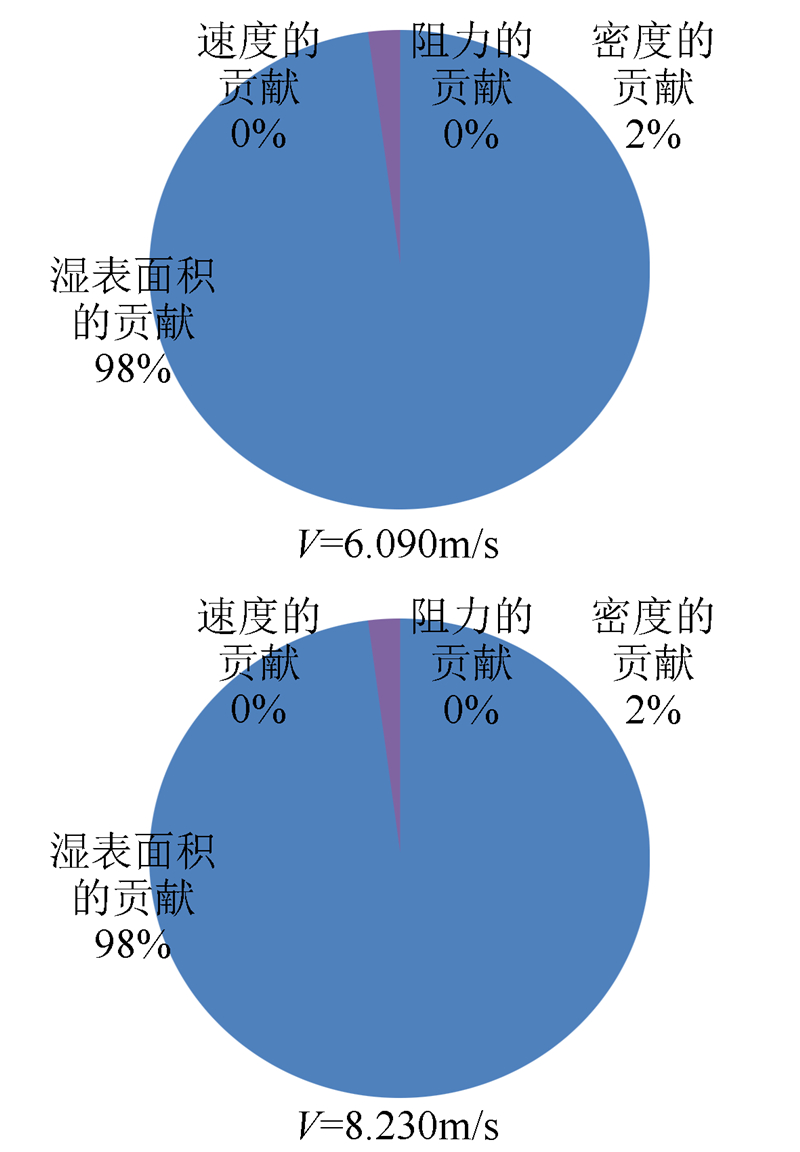 |
| 图 7 湿面积、速度、阻力、密度偏差极限分量在总阻力系数偏差极限中的贡献 Fig. 7 Contribution of surface,velocity,resistance,density bias limits to total resistance coefficient bias limit |
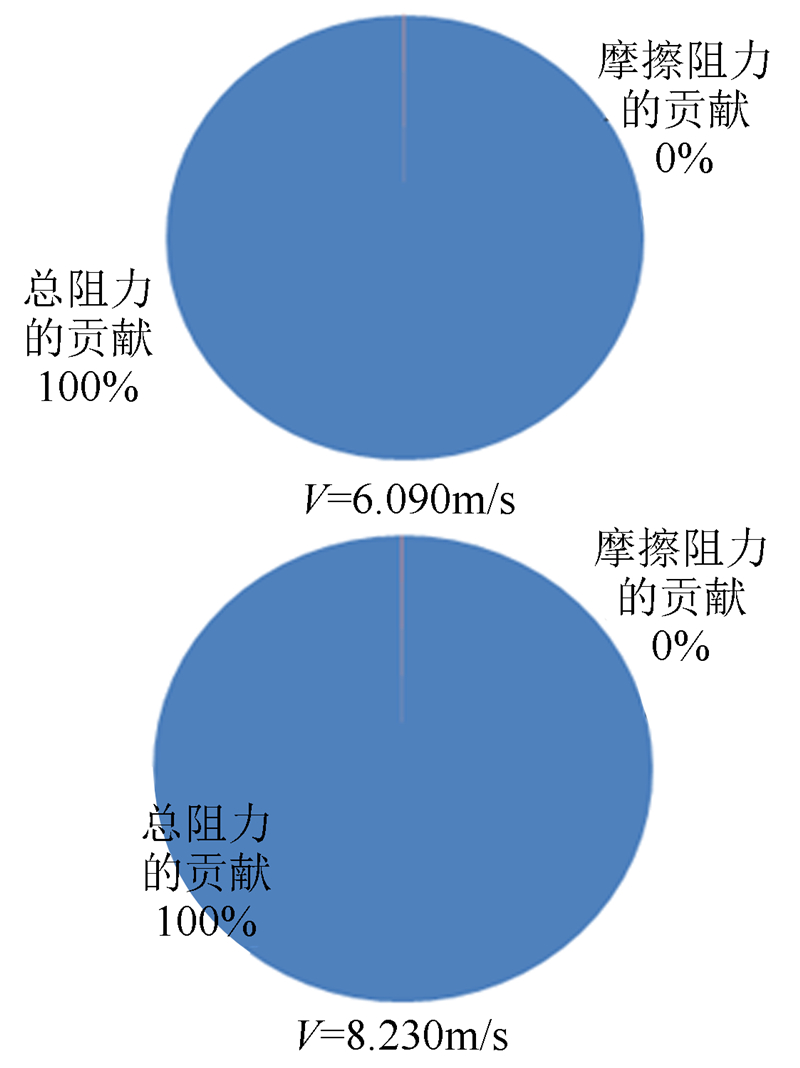 |
| 图 8 总阻力系数和摩擦阻力系数极限分量在剩余阻力系数偏差极限中的贡献 Fig. 8 Contribution of total resistance coefficient and friction resistance coefficient bias limits to residual resistance coefficient bias limit |
为了建立精密度极限,模型重复进行试验7次,从而得到重复试验的标准差。由于实验条件限制,此7次重复试验是在一次安装下完成的。本次试验由所测得的 阻力和速度来确定总阻力系数,根据1978年ITTC方法,修正到温度为15℃。首先根据公式(3),计算和温度无关的剩余阻力系数CR,再得到15℃时的总阻力系数。表 3和4为潜艇标模SUBOFF在速度V=6.090和8.230m/s时阻力试验结果,对总阻力系数CT和剩余阻力CR进行计算得到标准偏差。由表 3和4可知总阻力系数CT和剩余阻力系数CR都随 着速度的增加而减小,相应的标准偏差也是高速时更小一些,这也说明高速时试验结果更稳定。
| 试验 次数 | 测量值 | 名义速度常温 | ||
| R/N | CT/10-3 | CT15deg/10-3 | CR/10-3 | |
| 1 | 364.736 | 3.287 | 3.300 | 0.696 |
| 2 | 362.774 | 3.270 | 3.282 | 0.678 |
| 3 | 359.723 | 3.242 | 3.254 | 0.651 |
| 4 | 360.459 | 3.249 | 3.261 | 0.657 |
| 5 | 368.954 | 3.325 | 3.338 | 0.734 |
| 6 | 364.412 | 3.285 | 3.297 | 0.693 |
| 7 | 363.833 | 3.279 | 3.291 | 0.688 |
| 平均 | 363.556 | 3.289 | 0.685 | |
| 标准偏差 | 0.028 | 0.028 | ||
| 试验 次数 | 测量值 | 名义速度常温 | ||
| R/N | CT/10-3 | C15degT/10-3 | CR/10-3 | |
| 1 | 559.396 | 2.761 | 2.772 | 0.291 |
| 2 | 564.193 | 2.784 | 2.796 | 0.314 |
| 3 | 557.179 | 2.750 | 2.761 | 0.280 |
| 4 | 560.475 | 2.766 | 2.777 | 0.296 |
| 5 | 559.729 | 2.762 | 2.774 | 0.292 |
| 6 | 558.503 | 2.756 | 2.768 | 0.286 |
| 7 | 561.309 | 2.770 | 2.781 | 0.300 |
| 平均 | 560.112 | 2.776 | 0.294 | |
| 标准偏差 | 0.011 | 0.011 | ||
根据公式(10)和(11),可以计算得到多次试验和单次试验的精密度极限,结果如表 5所示。由表 5可知,无论是总阻力系统CT和剩余阻力系数CR,多次试验的精密度极限要比单次试验的精密度极限小,说明增加试验次数可以起到减小精密度极限的作用。
| 速度 /(m·s-1) | PCT(M) /10-3 | PCT(S) /10-3 | PCR(M) /10-3 | PCR(S) /10-3 |
| 6.090 | 0.021 | 0.055 | 0.021 | 0.055 |
| 8.230 | 0.008 | 0.022 | 0.008 | 0.022 |
根据公式(5)和(6),把多次试验和单次试验的精密度极限和偏差极限合并,则可计算7次试验平均值和单次试验的总不确定度。
| 速度 /(m·s-1) | UCT(M) /10-3 | UCT(S) /10-3 | UCR(M) /10-3 | UCR(S) /10-3 |
| 6.090 | 0.026 | 0.057 | 0.026 | 0.057 |
| 8.230 | 0.016 | 0.026 | 0.016 | 0.026 |
由表 6可知随着试验速度的提高,总阻力系数和剩余阻力系数的总不确定度降低。说明潜艇标模SUBOFF在高速时试验结果更加稳定。
2.4 试验结果的表达形式以V=8.230m/s为例,总阻力系数CT和剩余阻力系数CR的7次试验平均值的完整表达形式如下:
CT=(2.776±0.016)×10-3,置信概率p=95%;
CR=(0.294±0.016)×10-3,置信概率p=95%。
3 结 论通过该项试验研究工作,可以得出下列结论:
(1) 摩擦阻力系数的不确定度传递中,由温度引起的运动粘性系数的偏差极限占到97%,准确测量温度可以减少摩擦阻力系数的偏差极限。
(2) 总阻力系数的偏差极限98%来自于湿表面积的偏差极限,而剩余阻力系数的偏差极限几乎100%来自于总阻力系数的偏差极限,所以需提高模型的加工精度,用以降低湿表面积的偏差极限。
(3) 随着试验速度的提高,总阻力系数和剩余阻力系数的总不确定度降低,说明潜艇标模SUBOFF在高速时试验结果更加稳定。
| [1] | 蔡大明, 李定尊. 船舶水动力性能试验研究不确定度[M]. 无锡: 中国船舶科学研究中心, 2004. Cai Daming, Li Dingzun. Uncertainty analysis of ship hydrodynamic performance test[M]. Wuxi: China Ship Scientific Research Center, 2004. |
| [2] | 朱德祥, 张志荣, 吴乘胜, 等. 船舶CFD不确定度分析及ITTC临时规程的初步应用[J]. 水动力学研究与进展, 2007, 22(3): 363-370. Zhu Dexiang, Zhang Zhirong, Wu Chengsheng, et al. Uncertainty analysis in ship CFD and the primary application of ITTC procedures[J]. Journal of Hydrodynamics, 2007, 22(3): 363-370. |
| [3] | 周广利, 黄德波, 李凤来. 船模拖曳阻力试验的不确定度分析[J]. 哈尔滨工程大学学报, 2006, 27(3): 377-390. Zhou Guangli, Huang Debo, Li Fenglai. Uncertainty analysis of ship model towing resistance test[J]. Journal of Harbin Engineering University, 2006, 27(3): 377-390. |
| [4] | 周广利. 船模拖曳阻力试验的不确定度分析[D]. 哈尔滨: 哈尔滨工程大学, 2002. Zhou Guangli. Uncertainty analysis of ship model towing resistance test[D]. Harbin Engineering University, 2002. |
| [5] | 施奇, 杨大明, 尹赘凯. 拖曳水池船模阻力试验不确定度分析[J]. 江苏科技大学学报(自然科学版), 2010, 24(5): 428-433. Shi Qi, Yang Daming, Yin Yunkai. Uncertainty analysis of ship model resistance test in towing tank[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2010, 24(5): 428-433. |
| [6] | 谢疆宇, 吴军强, 钟世东, 等. 2.4m跨声速风洞大型飞机试验不确定度评估[J]. 实验流体力学, 2010, 24(6): 65-68. Xie Jiangyu, Wu Junqiang, Zhong Shidong, et al. Uncertainty analysis for large aircraft test in 2.4m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(6): 65-68. |
| [7] | 黄叙辉, 张征宇, 尹疆, 等. 高速风洞试验模型姿态角的视频测量及不确定度分析[J]. 实验流体力学, 2013, 27(5): 82-86. Huang Xuhui, Zhang Zhengyu, Yin Jiang, et al. Videogrammetry for model's attitude and its uncertainty in high-speed wind tunnel testing[J]. Journal of Experiments in Fluid Mechanics, 2013. 27(5): 82-86. |
| [8] | 王刚, 唐志共, 吕治国, 等. 激波风洞气动力试验不确定度影响因素分析[J]. 实验流体力学, 2013, 27(2): 87-90. Wang Gang, Tang Zhigong, Lyu Zhiguo, et al. Analysis of uncertainty for aerodynamic test in shock tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(2): 87-90. |
| [9] | 马向能, 孙张群, 冯俊. 测量不确定度分析在操纵性试验中的应用[J]. 船舶力学, 2004, 10(8): 52-61. Ma Xiangneng, Sun Zhangqun, Feng Jun. Uncertainty analysis in captive model test[J]. Journal of Ship Mechanics, 2004, 10(8): 52-61. |
| [10] | International Towing Tank Conference. 7.5-02-01-01 Guide to the expression of uncertainty in experimental hydrodynamics[S]. The 25th ITTC 2008: 1-17. |
| [11] | International Towing Tank Conference. 7.5-02-01-02 Testing and extrapolation methods, general uncertainty analysis in EFD, guidelines for resistance towing tank test[S]. The 22nd ITTC 1999: 1-5. |
| [12] | International Towing Tank Conference. 7.5-02-02-01 Resistance test[S]. The 26th ITTC 2011: 1-13. |
| [13] | International Towing Tank Conference. 7.5-02-02-02 Testing and extrapolation methods, general guidelines for uncertainty analysis in resistance towing tank tests[S]. The 25th ITTC 2008: 1-16. |
| [14] | 邱辽原. 潜艇粘性流场的数值模拟及其阻力预报的方法研究[D]. 华中科技大学, 2006: 41. Qiu Liaoyuan. Numerical simulation of the viscous flow over the submarine and method research on predicting its viscous resistance[D]. Huazhong University of Science and Technology, 2006: 41. |
| [15] | 马运义, 许建. 现代潜艇设计原理与技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012: 73. Ma Yunyi, Xu Jian. Design principle and technology of modern submarine[M]. Harbin: Harbin Engineering University Press, 2012: 73. |
| [16] | 苏玉民, 庞永杰. 潜艇原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2005: 12. Sun Yumin, Pang Yongjie. Submarine principle[M]. Harbin: Harbin Engineering University Press, 2005: 12. |