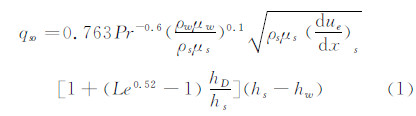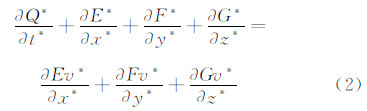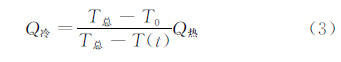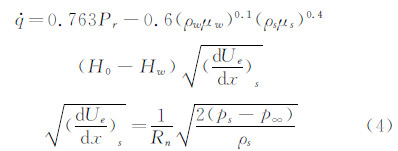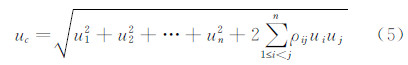临近空间高超声速飞行器外形复杂,要求长时间机动飞行,这就需要采用微烧蚀或非烧蚀材料保证飞行器外形基本不变。这类飞行器“保形”的要求对热 防护设计提出了很高的要求,也对飞行器热环境预测精度提出了很高的要求。
地面风洞热环境测量试验是获得高超声速飞行器表面热环境预测的一个重要途径。提高地面测热试验数据精度对防热结构设计、确保飞行安全是十分重要的。同时,精确的热环境测量数据也经常作为标准数据被用来校核气动热计算方法。因此,作为全机热环境数据核心的驻点热环境数据需要被细致研究,并不断地提高其准确性。
一直以来,国内外的研究人员都在为提高热环境预测结果而不断努力。在20世纪80~90年代,国际上对薄膜电阻温度计的测热原理、传热机理和数据处理方法开展了大量的研究,形成了准确可靠的测热数据处理方法。之后,国内外的研究大都集中于改善薄膜传感器的制作工艺和耐冲刷性能,并逐步发展了结构坚固的同轴热电偶和获取信息丰富的大面积测热技术。国外针对激波风洞中测热传感器的适用性、误差来源与分析等开展了大量的研究,并逐步形成了统一的方法和标准。
对薄膜电阻温度计而言,以Cook W. J和 Felderman E. J在1970年基于半无限假设推导得到的Cook-Felderman公式应用最为广泛[1, 2]。1988年3月,美国空军对薄膜热流传感器进行了数值分析,进一步验证了半无限假设应用于薄膜电阻温度计的合理性[3]。同年12月,该机构再次对薄膜传感器的使用范围、标定方法、数据处理方法进行了研究[4]。1992年,Rochester大学的John Lambropoulos教授详细研究了薄膜敏感部件的温度分布和传感器小型化对传感器热传导,以及接触热阻的影响[5]。在1997年,Kenneth[6]使用薄膜电阻温度计在激波风洞中测量了球头驻点的热环境并与Fay-Riddell公式进行了对比。Kenneth发现,试验模型尺寸较大时,数据处理结果与Fay-Riddell公式结果差别越来越大。他分析认为传感器的多维传热效应对测热结果影响较大,并计划采用数值方法分析试验模型测热点附近的流场情况,同时对传感器敏感部件区开展三维的有限元传热分析,但后续的研究结果未见公开报道。
对于同轴热电偶,早在1980年,Hedlund等人就研究了如何将同轴热电偶应用于高超声速风洞的表面热流测量[7]。在2007年,Joseph J. Coblish等人[8]沿用了基于一维半无限假设的数据处理方法[9]处理同轴热电偶的测量结果,分析认为热电偶材料的热物性参数选取对热电偶测量结果的影响较大,但是数据处理结果普遍高于试验中给定的热流值,这一问题还有待研究。
此外,国外在气动热测量误差控制和不确定度分析方面也进行了大量的研究工作。1995年,AIAA发布了关于风洞数据不确定度评价的标准[10](AIAA Standard S-071)。1999年,AIAA再次完善了这个标准,规范了风洞测试试验不确定度的应用方法[11]。Andrew Booker等人对空气动力学的一些变量作了统计模型和误差分析[12]。Ben H. Thacker等人采用FORM,SORM[13],AIS[14],AMV[15]等方法对误差和不确定度进行了随机工程分析[16]。经过近20年在误差控制和风洞测量标准方面的研究,在2007年,AEDC的9号风洞的热流误差范围已在4%以内[8]。
虽然国内外对于提高热环境预测精度的研究取得了较大进展,但是对于在风洞试验这种高强度瞬态传热条件下,传感器对试验模型局部流场的影响规律、同轴热电偶的传热机理研究和红外测热模型、磷光测热模型的传热机理研究未见相关报道。
为此,本文从传感器测温机理入手,研究传感器表面特性对局部流场和热流的影响、流场差异和读数方式对测热数据的影响,并给出相应的修正方法和误差分布。
1 球头驻点热流测量试验概况在飞行器热环境测量试验中,驻点热流测量值通常作为其他区域热流值的参考标准。因此,驻点热流测量的准确与否关系到整个飞行器热环境信息的准确性。本文以球头驻点的热环境测量试验为例开展了相关研究。
1.1 试验设备、测热模型与热流传感器驻点热流测量试验在中国空气动力研究与发展中心超高速所的Φ2mm激波风洞(见图 1)中进行,风洞喷口直径为2m,有效试验时间为10~30ms,风洞概况和详细参数见文献[17]。
 |
| 图 1 Φ2m激波风洞外形图 Fig 1 Φ2m shock wave tunnel |
热流测量传感器采用了Φ2mm、Φ1mm的薄膜电阻温度计和同轴热电偶热流传感器,以及模拟球头外形的型面薄膜电阻温度计,如图 3和4所示。
 |
| 图 2 试验模型安装情况 Fig 2 Test models in tunnel |
 |
| 图 3 平面薄膜电阻温度计 Fig 3 Flat surface thin film |
 |
| 图 4 同轴热电偶传感器 Fig 4 Coaxial thermal couples |
 |
| 图 5 型面薄膜电阻温度计 Fig 5 Curved surface thin film resistance thermometers |
风洞典型测热试验的来流参数如表 1所示。
| 流场 | Ⅰ | Ⅱ |
| 运行方式 | 缝合 | 亚缝合 |
| 驱动压力p4/MPa | 50.0 | 10.0 |
| 被驱动压力p1/MPa | 1.15 | 0.23 |
| 混合比X | 0.80 | 0.80 |
| 激波马赫数Ms | 2.61 | 2.59 |
| 总压p0/MPa | 35.82 | 7.14 |
| 总温T0/K | 1042.2 | 1030.1 |
| 马赫数M∞ | 10.31 | 10.05 |
| 自由流单位雷诺数Re∞/L/(1·m-1) | 2.10×107 | 4.30×106 |
| 自由流动压/MPa | 0.51 | 0.11 |
| 自由流密度/(kg·m-3) | 0.0466 | 0.0103 |
| 自由流静温/K | 48.4 | 50.9 |
| 自由流静压/Pa | 646.68 | 150.67 |
| 自由流速度/(m·s-1) | 1487.0 | 1461.7 |
本文采用成熟的气动热工程计算方法(驻点区计算采用Fay-Riddell公式)得到了试验状态下的球头驻点热环境数据,并采用基于N-S方程的气动热数值计算方法计算了2个流场条件下球头驻点附近的流场和热流分布情况。
Fay-Riddell驻点热流公式利用多罗得尼津-曼格勒变换和相似性假定,将高温气体边界层偏微分方程化为常微分方程,气体热力学特性、输运特性有关的无因次参数假设为一系列常数,利用萨特兰粘性律对驻点边界层方程进行计算分析,并总结出下述参数的计算公式:
式中: hs=0.5u∞+T∞Cp—驻点焓; hw=TwCp—壁面焓; ρw,μw,hw—壁面处的密度、粘性系数、焓值; ρs,μs,hs—驻点处的密度、粘性系数、焓值; hD=∑Cis.hoi,i=O,N—空气的平均离解焓。气动热数值计算为求解笛卡尔坐标系下,守恒形式的三维非定常可压缩Navier-Stokes方程:
求解格式采用LU-SGS隐式求解方法,正负通量的计算采用Von Leer通量分裂方法,控制面插值采用NND格式[18]。
典型试验状态下的驻点热流的计算结果如图 6~8所示,并将计算结果作为与试验测量结果对比的 标准数据。
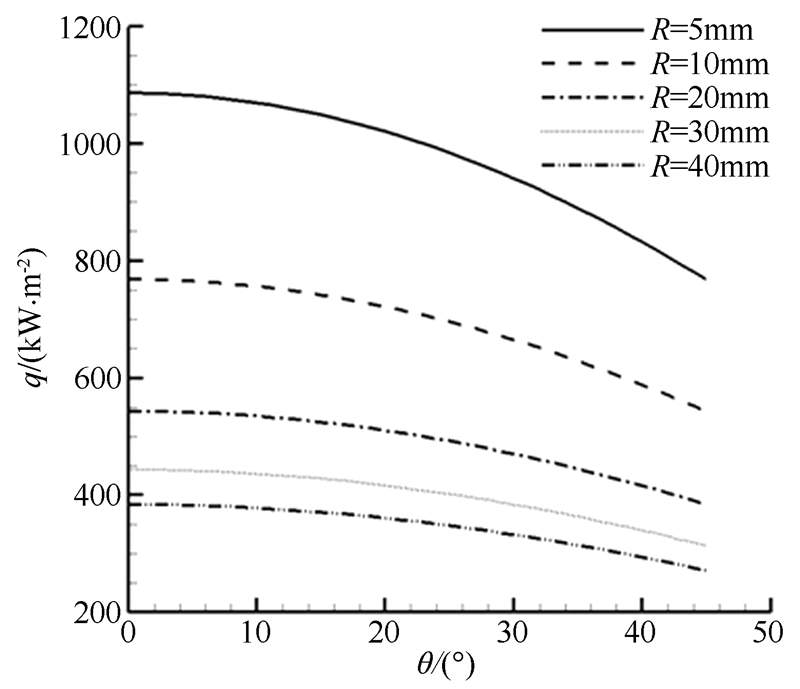 |
| 图 6 球头热流随θ角分布(流场Ⅰ) Fig 6 Heat flux distribution of ball head with θ (flow field Ⅰ) |
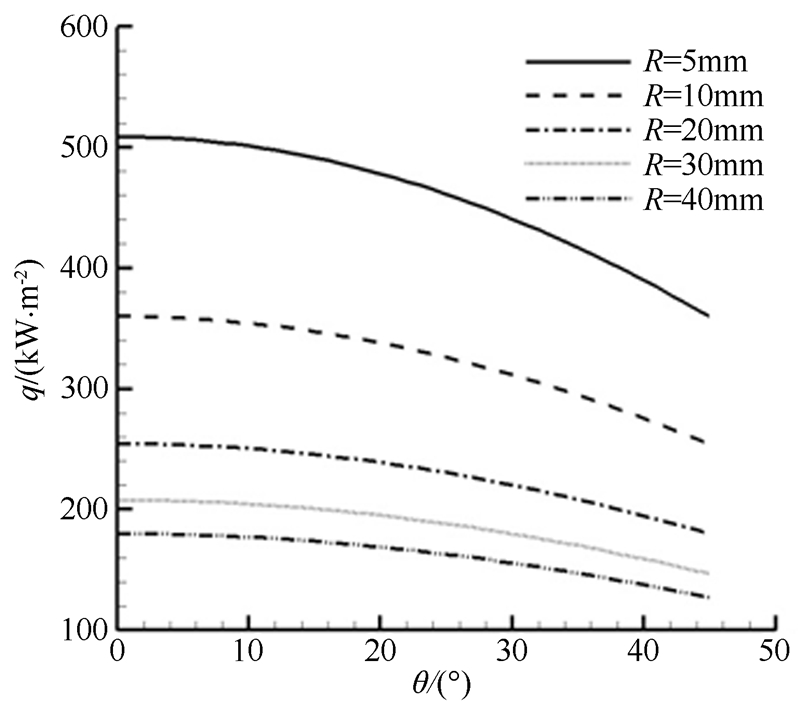 |
| 图 7 球头热流随θ角分布(流场Ⅱ) Fig 7 Heat flux distribution of ball head with θ (flow field Ⅱ) |
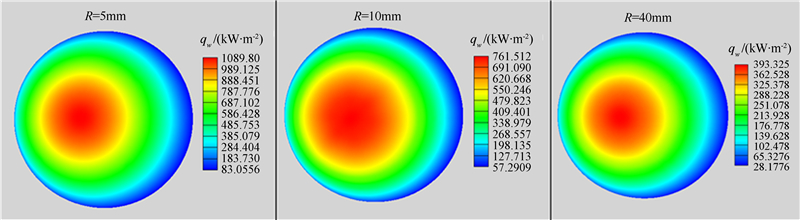 |
| 图 8 球头表面热流分布图(气动热数值方法,流场Ⅰ) Fig 8 Heat flux distribution of ball head (N-S, flow field Ⅰ) |
本文采用文献[17]中建立的由温度-热流的热传导反问题计算方法,将试验中传感器温度测量数据处理为热流信息。为了深入研究实验过程本身存在的误差,文献[17]详细分析了数据处理方法的可靠性,由于文章篇幅受限,在此不作详细介绍。
测热试验数据处理结果如图 9、10和表 3、4所示。可见,当试验模型半径小于10mm时,热流试验数据处理结果略低于计算结果;当试验模型半径大于 10mm时,热流数据处理结果逐渐高于计算结果(见图 11)。这与1997年Kenneth[6]发现的现象是一致 的(见表 2)。另外,由表 3可见,热流测量结果从高到低为:型面传感器、Φ1mm传感器、Φ2mm传感器,这说明测热传感器尺寸会对测热结果造成一定的影响。
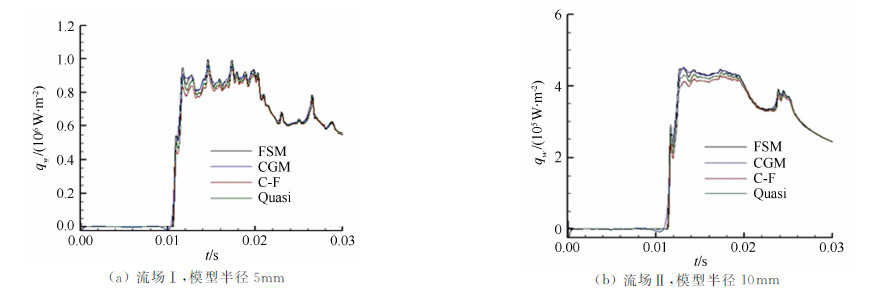 |
| 图 9 数据处理热流信息(薄膜电阻温度计) Fig 9 Heat flux information obtained by data processing (Flat surface film-thin sensor) |
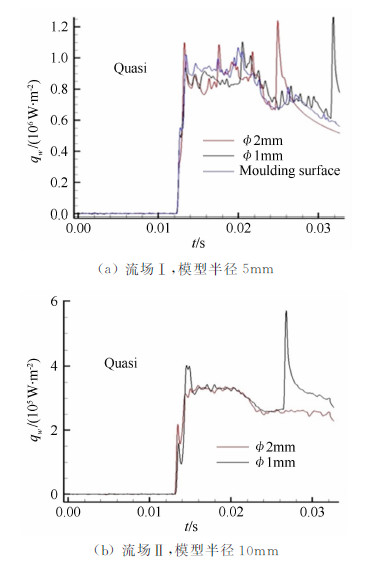 |
| 图 10 不同类型薄膜电阻温度计测热结果对比 Fig 10 Comparison of heat flux measurements via different types of film-thin sensors |
|
Run # | Test Cond | 1/2”Hem BUT/FT2-sec | 1/2”Q0FR BUT/FT2-sec | 1/2”Hem BUT/FT2-sec | 1/2”Q0FR BUT/FT2-sec | 1/2”Hem BUT/FT2-sec | 1/2”Q0FR BUT/FT2-sec | 1/2”Hem BUT/FT2-sec | 1/2”Q0FR BUT/FT2-sec |
|
889 890 | 4 4 | 75.72 76.88 | 74.00 73.88 | 61.65 62.72 | 60.42 60.32 | 52.46 54.10 | 46.80 46.72 | 36.18 36.04 | 30.21 30.16 |
|
891 892 | 5 5 | 263.50 256.60 | 248.00 250.40 | 214.40 215.00 | 202.50 204.43 | 183.50 176.40 | 156.90 158.40 | 108.50 109.90 | 101.30 102.20 |
| 894 | 2 | 204.50 | 200.40 | 181.40 | 163.61 | 154.60 | 126.70 | 106.10 | 81.81 |
| 895 | 3 | 147.40 | 141.50 | 122.50 | 115.50 | 99.02 | 89.47 | 64.18 | 57.75 |
| 896 | 1 | 352.30 | 352.30 | 295.90 | 287.66 | 269.90 | 222.80 | 219.30 | 143.80 |
| 球头 半径 /mm | Φ2mm 铂薄膜热 流传感器 | Φ1mm 铂薄膜热 流传感器 | 型面 热流 传感器 | F-R 公式 结果 | 数值 计算 结果 | |
| 流场Ⅰ | 5 | 903.6 | 947.3 | 960.5 | 1086 | 1089.8 |
| 10 | 723 | 742.2 | 760. | 767.9 | 761.5 | |
| 15 | 668.8 | 677.5 | 02.1 | 627 | 629.2 | |
| 20 | 562.2 | 585 | 570.4 | 543 | 526.3 | |
| 25 | 511.8 | 576.7 | 553.5 | 485.6 | 487.4 | |
| 30 | 525.1 | 535.6 | 534.3 | 443.4 | 444.9 | |
| 35 | 506 | 511.7 | 513.9 | 410.5 | 411.9 | |
| 40 | — | 449.8 | 479.6 | 384 | 393.3 | |
| 流场Ⅱ | 5 | 424.8 | 436.4 | 448.6 | 508.7 | 509.2 |
| 10 | 336.7 | 334.1 | — | 359.7 | 360.0 | |
| 15 | 302 | 321.2 | 319.1 | 293.7 | 294.0 | |
| 20 | 261.3 | 268.2 | 270.5 | 254.3 | 254.6 | |
| 25 | 240.6 | 252.2 | 245 | 227.5 | 227.7 | |
| 30 | 222 | 236.4 | 244.5 | 207.7 | 207.9 | |
| 35 | 212.3 | 222.9 | 220.9 | 192.3 | 192.4 | |
| 40 | 200.6 | 214.9 | 217.9 | 179.8 | 180.0 |
| 传感器直径 | 试验模型半径 | 数据处理 | F-R公式 | 数值计算 |
| 2mm | 5mm | 885.6 | 1086 | 1089.8 |
| 10mm | 749.2 | 767.9 | 761.5 | |
| 20mm | 572.4 | 543 | 526.3 | |
| 25mm | 540.3 | 485.6 | 487.4 | |
| 30mm | 524.1 | 443.4 | 444.9 | |
| 35mm | 457.6 | 410.5 | 411.9 | |
| 40mm | 445.1 | 384 | 393.3 | |
| 1mm | 5mm | 934.6 | 1086 | 1089.8 |
| 10mm | 756.1 | 767.9 | 761.5 | |
| 25mm | 550.7 | 485.6 | 487.4 |
图 9、19~22中的FSM为顺序函数法,CGM为共轭梯度法、C-F为基于一维半无限假设的Cook-Felderman方法、Quasi为准定常逼近法。
2 传感器表面特性造成的误差形成机理与影响规律研究通过计算分析,发现出现图 11中现象的原 因是由于传感器安装带来的局部曲率变化引起了局部流场变化,以及传感器表面敏感元器件温升造成了加热量下降而引入了误差。本节计算研究了这些误差的形成机理和影响规律,并给出了相应的修正方法。
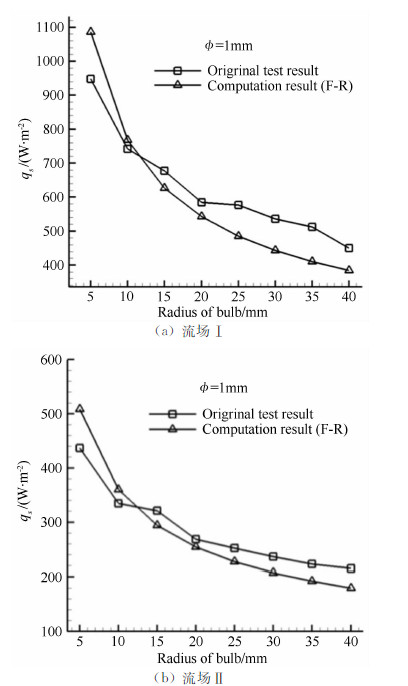 |
| 图 11 测热试验数据与计算结果的对比 Fig 11 Comparison between measurement and computation for heat flux |
薄膜电阻温度计和同轴热流传感器表面是“平”的,而试验模型表面存在一定的曲率变化。由图 12可见在安装传感器后球头试验模型的驻点区域热环境发生了变化。图 13给出了在r/R=0.1和0.2时“削平”区域半径上的热流变化情况与未“削平”时的对比。在被“削平”区域的中心其热流值较未“削平”时偏低,而在“削平”区域的边缘其热流值高于未“削平”时。图 14给出了“削平”区域热流沿轴向的变化。
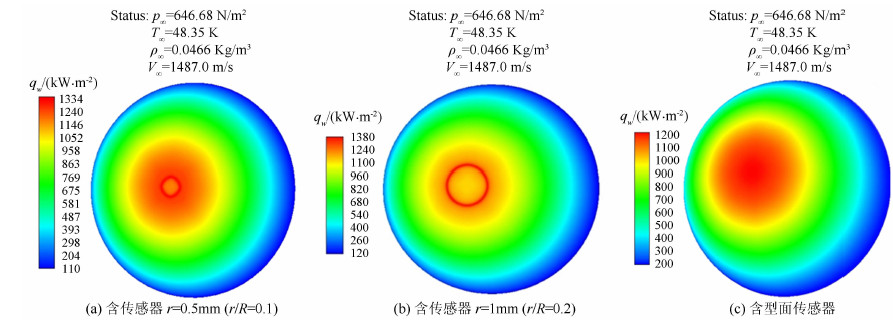 |
| 图 12 试验条件下R=5mm球头表面热流分布 Fig 12 Heat flux distribution of R=5mm ball head under test condition |
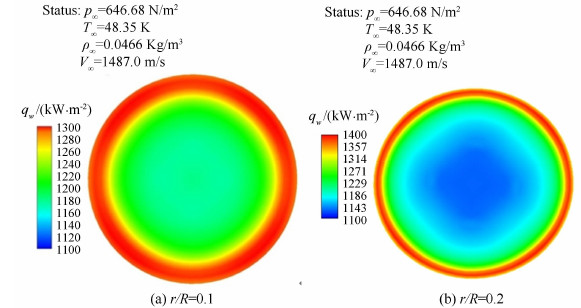 |
| 图 13 “削平”局部区域热流分布 Fig 13 Heat flux distribution in flat region |
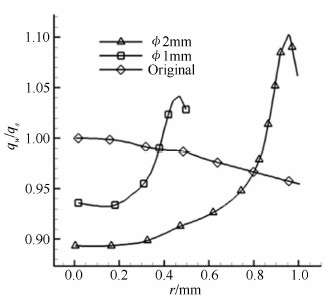 |
| 图 14 “削平”区域热流沿轴向变化 Fig 14 Heat flux variation along radius |
考察薄膜电阻温度计和同轴热电偶测温敏感元件的位置,结合块状电阻阻值计算公式[19],进行分析可知,Φ2mm传感器有效敏感元件为Φ1~1.4mm的S形元件,Φ1.4~2mm间的部分是引线位置(见图 15);Φ1mm传感器的有效敏感元件是宽为Φ0.6mm内的S形元件,两边Φ0.6~1mm间的部分是引线位置(见图 16)。结合图 14可知,对于R=5mm的试验 模型,Φ1mm 传感器(即r/R=0.1时)中间敏感区域的热流值为驻点热流值 的93.3%~95.2%,平均减小量约为6%;Φ2mm传感器(即r/R=0.2时)中间敏感区域的热流值为驻点热流值的89.3%~91.7%,平均减小量约为9.5%。
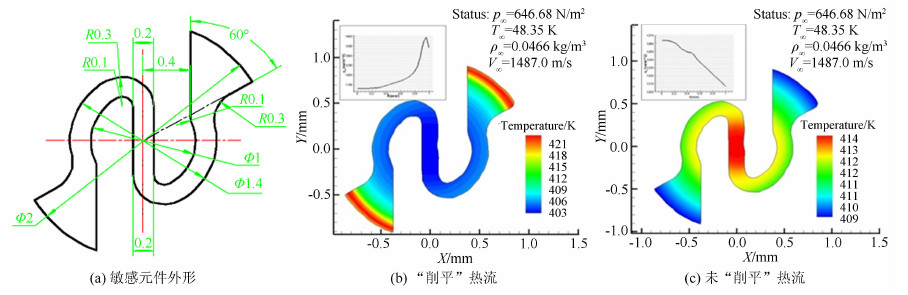 |
| 图 15 Φ2mm薄膜电阻温度计表面敏感元件传热特性分析 Fig 15 Thermal conduction analysis of sensitive element of Φ2mm thin-film sensor |
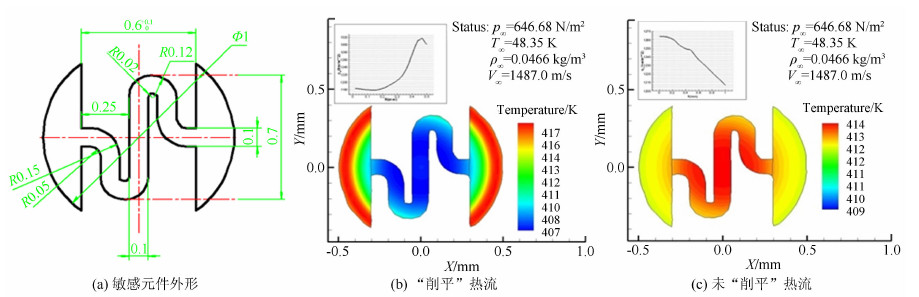 |
| 图 16 Φ1mm薄膜电阻温度计表面敏感元件传热特性分析 Fig 16 Thermal conduction analysis of sensitive element of Φ1mm thin-film sensor |
结合图 14,对于R=5mm的试验模型, 在测热试验过程中,模型和传感器由于受到气动加热,表面温度会有所升高。由测量得到的电信号(即表面温度信号)直接转换得到热流信息是热壁热流信息,需要通过转换得到冷壁热流值才能应用于后期的烧蚀试验和防热设计,这种热壁修正适用于总焓大于900kJ/kg的中高焓值条件。对风洞试验,一般采用总温代替总焓,用壁面温度代替壁面焓值。实际上随着传感器表面温度的升高,进入到传感器内部的热流是逐渐降低的。热壁热流与冷壁热流的关系可以用测试风洞的总温和传感器被加热面的温度来确定,详见公式(3)。
以流场Ⅰ的试验条件为例,风洞运行总温约为1000K,R=5mm球头下驻点热流值约为1MW/m2的冷壁热流,对于薄膜电阻温度计而言,考虑表面温升与热流的耦合效应,在5ms时进入传感器内部的
热流为冷壁热流的92%,在10ms之后进入传感器内部的热流为冷壁热流的88%,表面温升比不考虑壁温变化耦合效应的情况下低了近10%。 采用2.1节的尺度效应分析数据和2.2节的热壁修正公式对Φ2mm薄膜电阻温度计的测热结果进行了修正,修正结果如表 5和图 18所示。可见在数据修正之后,小球头试验模型的测热结果与计算结果基本吻合,随着试验模型球头半径的增大,试验测试结果逐渐高于计算结果。Kenneth M认为这种现象的出现与风洞的来流参数和风洞流场分布是相关的,定量的研究分析还有待进一步开展。 热流测量是一种间接测量,试验测量中涉及参数的不确定性因素包括来流流场、传感器特征参数、传感器安装工艺、传感器重复使用次数和有效测热时间选取等。
通过分析Fay-Riddell驻点热流公式,可得到公式(4),由此计算了由于总温、总压和马赫数的参数偏差而引起的驻点热流误差。从表 6的计算结果来看,在总温和马赫数不变的情况下,总压偏差在4%时,热流的偏差在2.45%左右;在总压和马赫数不变的情况下,总温偏差4%时,热流的偏差在6%左右。另外,来流马赫数的变化会引起驻点热流的较大变化,来流马赫数偏差1%,驻点热流偏差约2.5%。 本文中激波风洞的有效测热时间为5~10ms,例如在图 19所示的热流曲线中,选取15~20ms之间相对比较平滑的一段为有效测热时间,并将这段曲线的平均值作为测量热流值。但是,在实际操作中,热流相对平滑段的选取是人为决定的,不同操作人员选取的有效测热时间段略有不同,表 7给出了不同时间段选取得到的有效热流值情况。此外,有些试验车次由于受到来流流场脉动的影响,热流数据“跳跃”较大(见图 20),这对有效测热时间段的选取也造成一定的影响。 从表 7可见,当试验测量得到的热流曲线较平滑时,选取不同有效热流时间得到的热流结果相差不大(偏差<1%)。但是,当试验测量得到的热流曲线有一定“跳跃”时,选取不同有效热流时间得到的热流结果可能与多次取值得到平均热流的结果有一定差别。 在重复性测量中,测量误差往往是随机误差,而随机误差又是用表征其取值分散性的标准不确定度来评定的。因此,需要在随机误差传播基本公式的基础上推导出间接测量标准差传播的基本公式,也就是间接测量标准不确定度评定的基本公式。参考文献[20]详细对此进行了推导,得到:
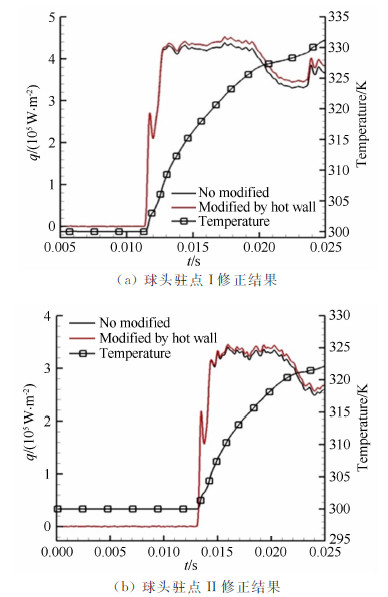
图 17 薄膜电阻温度计测热数据壁温修正结果
Fig 17 Heat flux results modified by wall temperature of thin film sensor
流场 试验球头
半径/mm原始测
试结果壁温效应
修正后结果曲率效应
修正后结果计算
结果
Ⅰ
5 903.6 981.4 1059.9 1086
10 723 768.7 807.1 767.9
15 668.8 711.4 732.7 627
20 562.2 595.2 607.1 543
25 511.8 541.3 548.3 485.6
30 525.1 551.2 556.7 443.4
35 506 529.0 532.1 410.5
40 — — — 384
Ⅱ
5 424.8 450.8 492.3 508.7
10 336.7 347.2 371.53 359.7
15 302 315.6 331.4 293.7
20 261.3 272.5 283.4 254.3
25 240.6 249.8 257.3 227.5
30 222 230.5 235.1 207.7
35 212.3 217.5 219.7 192.3
40 200.6 204.8 205.8 179.8 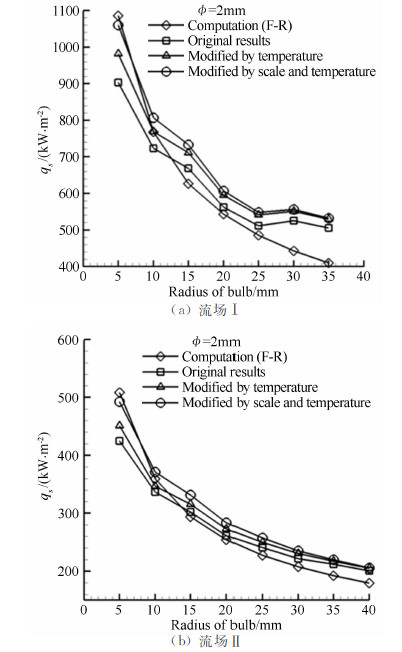
图 18 Φ2mm传感器的试验修正结果与计算结果的比较
Fig 18 Comparison between modified test results and computation results for Φ2mm sensor
流场Ⅰ:T0=931.5K,Ma=10.21 流场Ⅱ: T0=939.88K,Ma=10.03
总压
/MPa总压
偏差热流
/(kW·m-2)热流
偏差总压
/MPa总压
偏差热流
/(kW·m-2)热流
偏差
33.34 1.24% 1093.02 0.65% 7.74 1.50% 513.43 0.93%
32.63 -0.91% 1080.83 -0.48% 7.51 -1.50% 504.17 -0.89%
33.92 3% 1102.87 1.55% 7.92 4% 520.92 2.40%
31.94 -3% 1068.86 -1.58% 7.32 4% 496.16 -2.47%
流场Ⅰ:p0=32.93MPa,Ma=10.21 流场Ⅱ: p0=7.62MPa,Ma=10.03
总温
/K总温
偏差热流
/(kW·m-2)热流
偏差总温
/K总温
偏差热流
/(kW·m-2)热流
偏差
941.1 1.03% 1102.99 1.56% 947 0.76% 514.53 1.15%
919 -1.34% 1063.91 -2.03% 922.3 -1.87% 494.33 -2.82%
959.44 3% 1135.49 4.56% 977.48 4% 539.51 6.06%
903.5 -3% 1036.65 -4.54% 902.28 -4% 478.01 -6.03%
流场Ⅰ:p0=32.93MPa,T0=931.5K 流场Ⅱ:p0=7.62MPa,T0=939.88K
马赫数 马赫数
偏差热流
/(kW·m-2)热流
偏差马赫数 马赫数
偏差热流
/(kW·m-2)热流
偏差
10.29 0.44% 1073.15 -1.18% 10.08 0.48% 501.53 -1.41%
10.19 -0.53% 1099.05 1.20% 9.98 -0.52% 515.96 1.43%
10.31 1% 1059.68 -2.49% 10.13 1% 494.45 -2.80%
10.11 -1% 1112.32 2.51% 9.93 -1% 523.31 2.87% 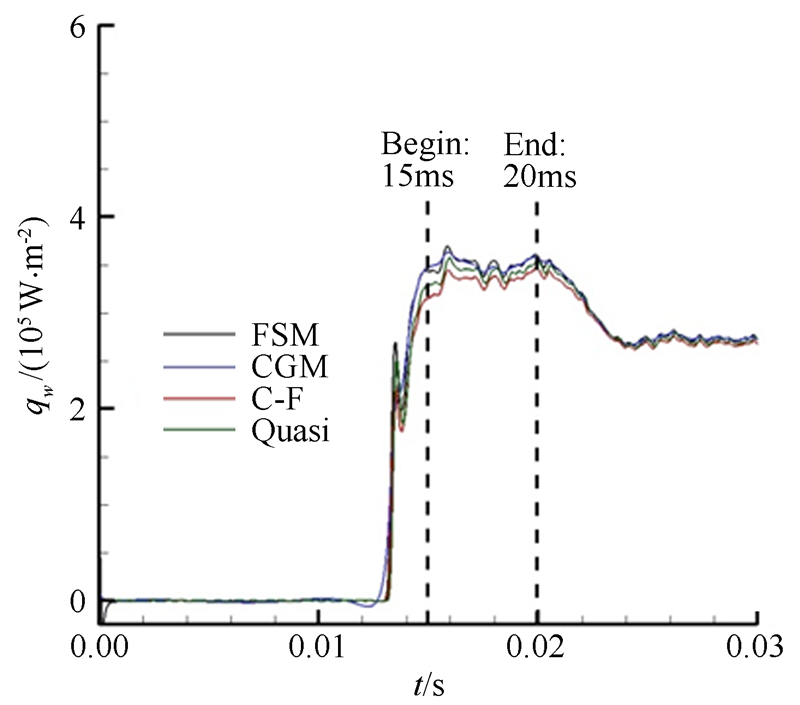
图 19 有效热流值起始位置示意(车次A)
Fig 19 Selection of effective heat flux (round A)
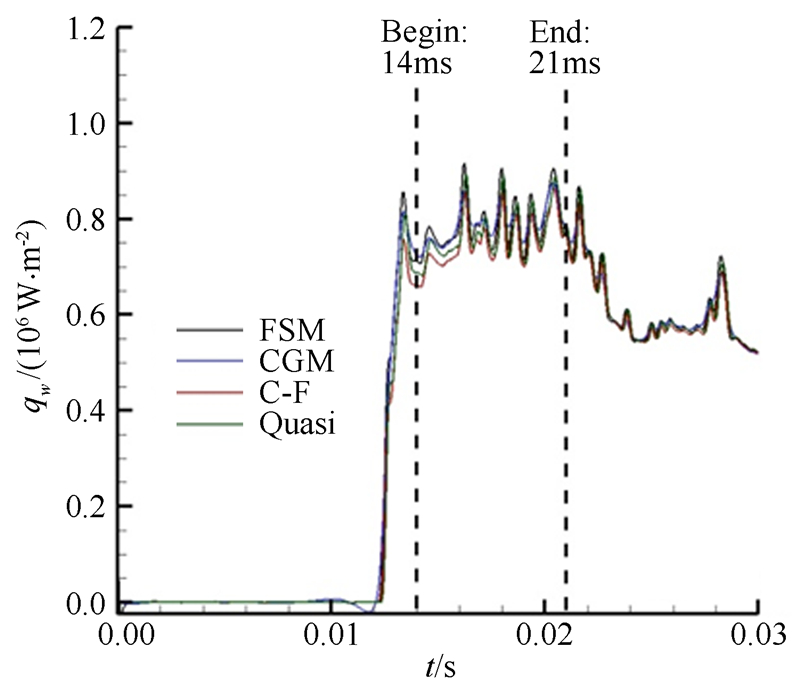
图 20 有效热流值起始位置示意(车次B)
Fig 20 Selection of effective heat flux (round B)
车次A 车次B
判读起
止时间
/ms判读
热流值平均
热流值偏差 判读起
止时间
/ms判读
热流值平均
热流值偏差
B: 15
E: 20
B: 15
E: 19
B: 15
E: 18
B: 16
E: 19
B: 16
E: 20
359.9
358.9
360.6
358.7
360.0
359.6
0.07%
0.2%
0.27%
0.25%
0.1%
B: 14
E: 21
B:15
E: 21
B: 16
E: 21
B: 15
E: 20
B: 16
E: 20
834.3
845.9
858.1
835.4
848.1
844.4
1.1%
0.18%
1.6%
1.1%
0.44%
u1,u2,…,un为直接测量量引起的间接测量值的标准不确定度分量;
ρij为第i个测量值的不确定度和第j个测量值的不确定度之间的相关系数。
根据式(5)对同轴热电偶和薄膜电阻温度计的验证试验(流场Ⅰ和流场Ⅱ)进行了测热热流的不确定度评定。
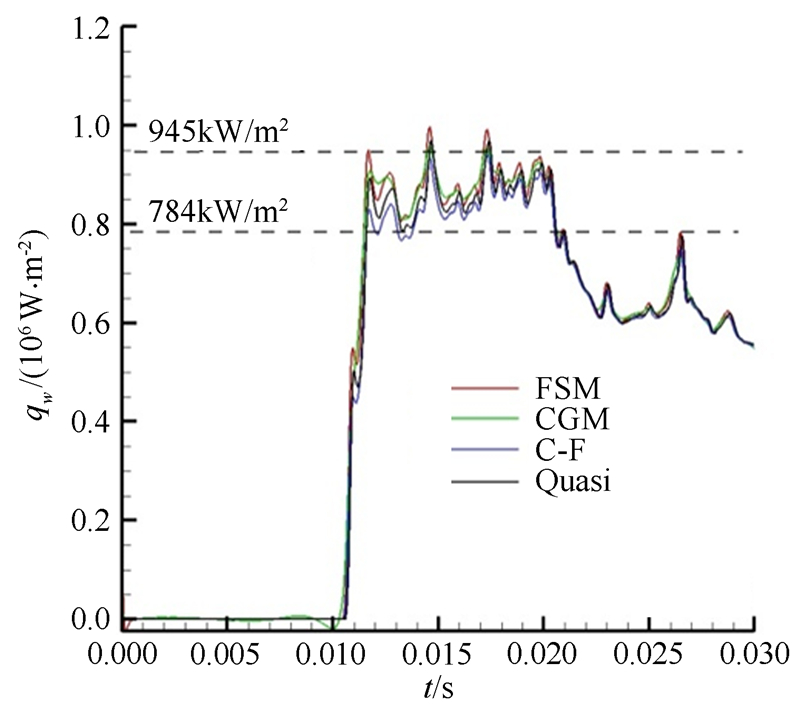 |
| 图 21 流场Ⅰ试验数据的不确定度分析(R=5mm) Fig 21 Uncertainty analysis of test data under flow field Ⅰ condition (R=5mm) |
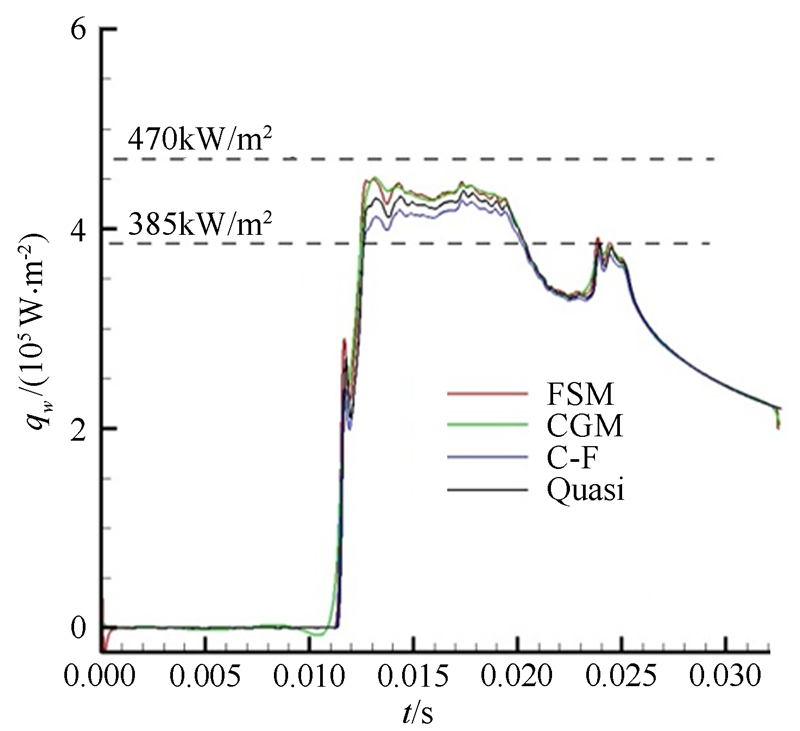 |
| 图 22 流场Ⅱ试验数据的不确定度分析(R=5mm) Fig 22 Uncertainty analysis of test data under flow field Ⅱcondition (R=5mm) |
根据本节的分析,对于流场Ⅰ,总压对热流的影响量最大为0.64%,总温对热流的影响量最大为-2.03%,马赫数对热流的影响量最大为-1.20%,传感器重复使用对热流的最大影响量为5%。另外,本文认为这几方面的影响因素间是互不相关的。
因此在不考虑其他因素的情况下,流场Ⅰ条件下R=5mm模型的热流测量不确定度为:
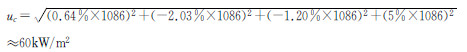
同样对于流场Ⅱ,总压对热流的影响量最大为1.55%,总温对热流的影响量最大为-2.82%,马赫数对热流的影响量最大为-1.43%,传感器重复使用对热流的最大影响量为5%。流场Ⅱ条件下R=5mm模型的热流测量不确定度为:
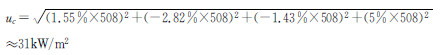
测热试验不确定度的获得有利于进一步精选测热试验中的原始热流结果,剔除粗大误差。
4 结论与展望本文详细分析了激波风洞中驻点热流测量试验中的误差源,并通过分析误差的组成情况,对测热试验进行了修正和分析,结论如下:
(1) 采用气动热数值计算方法,详细分析了传感器安装后驻点区曲率变化引起的流场变化和热流变化,根据不同传感器的类型和敏感元件的组成情况,并结合不同流场条件下的传感器传热计算分析,给出了修正方法和修正系数,是Kenneth在1997年观点的延续和拓展;
(2) 研究了传感器表面温升与热流之间的相互影响关系,考虑到总焓和壁面焓值的相互关系给出了测试热流的修正公式;
(3) 考虑到传感器安装后驻点区曲率变化因素和传感器表面温升与热流的相互影响关系,修正了测热试验数据处理结果。修正后的数据与理论计算数据吻合趋势有所改善;
(4) 计算了来流流场的微小变化对热流的影响,分析了人为读数、传感器重复使用等随机因素对热流测量的影响,并结合随机误差分析理论给出了不确定度的评定方法,计算得到了验证试验中热流测量的不确定度。不确定度评定方法的建立可以方便地剔除无效数据。
本文的研究成果已应用于我国高超声速飞行器地面热环境测量试验中,进一步提高了测热数据的精度。未来将进一步完善针对不同风洞的不确定度评定方面的工作,尽快形成测热试验的标准流程,建立针对不同风洞测热数据的不确定度评定标准。另外,将误差修正方法和不确定度分析方法更好集成到测热试验数据后处理软件中,方便试验人员操作使用,在提高测热精度的同时进一步提高测热试验效率。
| [1] | Cook W J, Felderman E J. Reduction of data from thin-film heat transfer gages: a concise technique[J]. AIAA J, 1970, 8(7): 1366-1368. |
| [2] | Cook William J. Unsteady heat transfer to a semi-infinite solid with arbitrary surface temperature history and variable thermal properties[R]. IOWA State University, ISU-ERI-AMES-675000, 1970. |
| [3] | Joseph A B. A numerical investigation of thin-film heat transfer gages[R]. ADA206134, 1989. |
| [4] | Gorald W W. An experiment method of testing yhin-film heat transfer gages[R]. ADA202605, 1988. |
| [5] | Lambrppoulos John. Mechanics of thin films[R]. AD-A247848, 1992. |
| [6] | Kenneth M C. Stagnation heat transfer measurement techniques in hypersonic shock tunnel flows over spherical segments[C]. The 32nd AIAA Thermophysics Conference, Atlanta, GA, 1997. |
| [7] | Hedlund E R. Heat transfer testing in the NSWC hypervelocity wind tunnel using coaxial surface thermocouples[R]. NSWC MP 80-151, 1980. |
| [8] | Joseph J Coblish, Stuart M Coulter, Joseph D Norris. Aerothermal measurement improvements using coaxial thermocouples at AEDC hypervelocity wind tunnel No.9[R]. AIAA-2007-146. |
| [9] | Boyd C F, Howell A. Numerical investigation of one-dimensional heat-flux calculations[R]. Silver Spring, NSWCDD/TR-94/114. |
| [10] | American Institute of Aeronautics and Astronautics. S-071-1995 Assessment of wind tunnel data uncertainty[S]. Reston, VA: 1801 Alexander Bell Drive, 1995. |
| [11] | American Institute of Aeronautics and Astronautics. S-071A-1999 Assessment of experimental uncertainty with application to wind tunnel testing[S]. Reston, VA: 1801 Alexander Bell Drive, 1999. |
| [12] | Booker Andrew, Ferguson David. Statistical models and error analysis for aerodynamic variables[R]. AIAA-2000-2696. |
| [13] | Madsen H O, Krenk S, Lind N C. Method of structural safety[M]. New Jersey: Prentice-Hall Inc, 1986. |
| [14] | Wu Y T. Computational method for efficient structural reliability sensitivity analysis[R]. AIAA-1993-1626. |
| [15] | Wu Y T, Millwater H R, Cruse T A. Advanced probabilistic structural analysis methods for implicit performance functions[R]. AIAA-1989-1371. |
| [16] | Ben H Thacker, David S Riha, Harry R Millwater. Errors and uncertainties in probabilistic engineering analysis[R]. AIAA-2001-1239. |
| [17] | 曾磊. 测热试验数据后处理方法及误差机理分析[D]. 四川绵阳: 中国空气动力研究与发展中心, 2012. Zeng lei. Study on data processing method and error mechanism analysis of heat flux measurement in wind tunnel[D]. Mianyang, Sichuan: China Aerodynamics Research and Development Center, 2012. |
| [18] | 朱自强, 吴子牛, 李津, 等. 应用计算流体力学[M]. 北京: 北京航空航天大学出版社, 1997. |
| [19] | 温宇峰, 祖光裕, 胡明, 等. Pt薄膜热敏电阻工艺研究[J]. 电子元件与材料, 2009, 21(9):9-10. Wen Yufeng, Zu Guangyu, Hu Ming, et al. Study on Pt thin film thermal resistor technology[J]. Electronic Components & Materials, 2009, 21(9):9-10. |
| [20] | 李金海. 误差理论与测量不确定度评定[M]. 北京: 中国计量出版社, 2003. |